Слайд 1Планирование эксперимента.
Анализ результатов.
Планирование 2-го порядка.
Слайд 2Пример проведения планирования 1-го порядка.
Постановка задачи
Покупатели приходят в магазин с
одним продавцом.
Время между приходом покупателей и время обслуживания подчиняются экспоненциальному
закону.
Необходимо определить функциональную зависимость между временем прихода, временем обслуживания и средним временем нахождения покупателя в очереди:
Тср.оч.= f(Тприх, Тобсл) - ?
Предполагаем линейную зависимость.
Пусть время прихода – в пределах от 5.0 до 6.0 мин.
время обслуж. – в пределах от 3.5 до 3.8 мин.
Тогда: -1 +1
Тприх: 5 6
Тобсл: 3.5 3.8
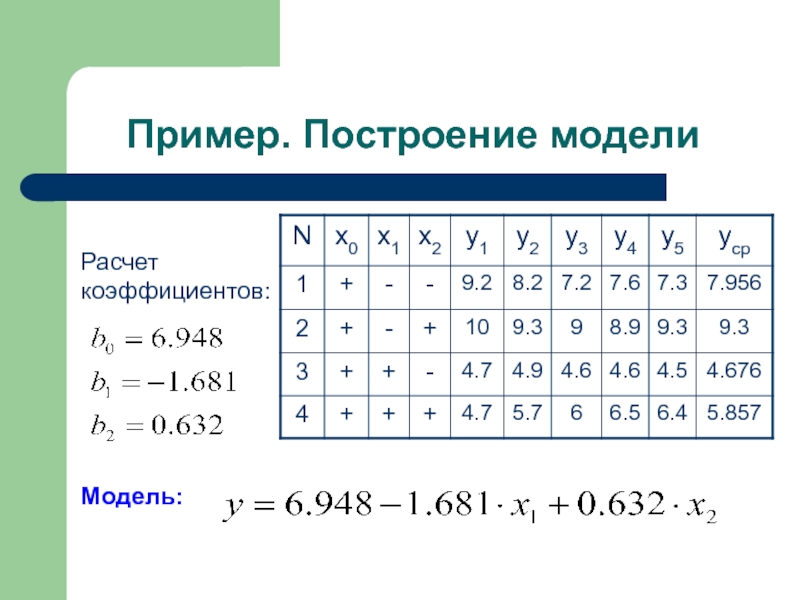
Слайд 3Пример. Построение модели
Расчет коэффициентов:
Модель:
Слайд 4Пример. Проверка адекватности
Выборочная дисперсия:
Дисперсия адекватности:
Критерий Фишера:
Модель адекватна
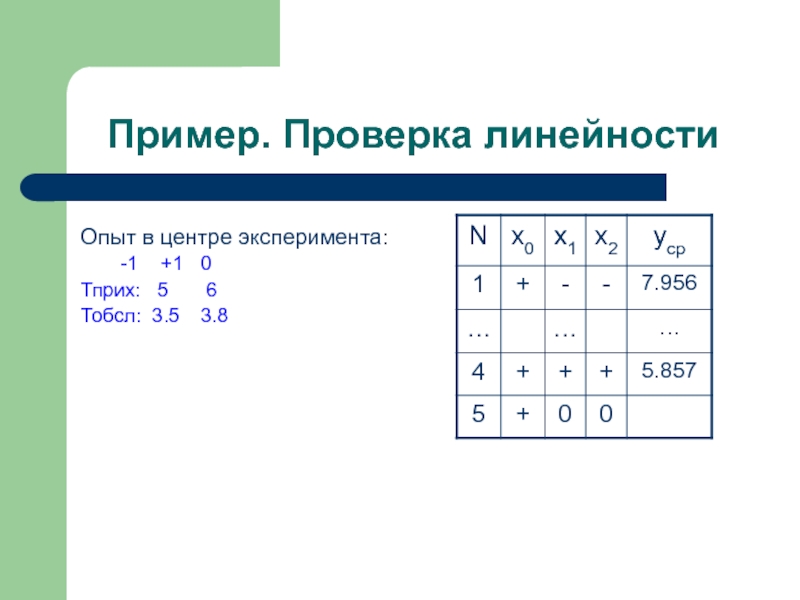
Слайд 5Пример. Проверка линейности
Опыт в центре эксперимента:
-1 +1 0
Тприх: 5 6
Тобсл: 3.5 3.8
Слайд 6Пример. Проверка линейности
Опыт в центре эксперимента:
-1 +1 0
Тприх: 5 6 5.5
Тобсл: 3.5 3.8 3.65
Критерий
Стьюдента:
Модель НЕ линейна
Слайд 7Пример. Проверка значимости коэффициентов
Модель:
Критерий Стьюдента:
Коэффициенты:
Значим
НЕ Значим
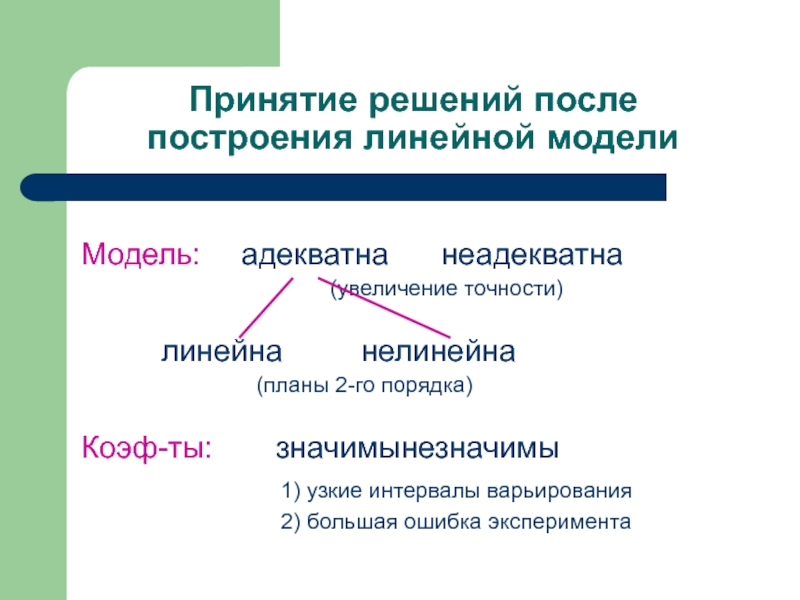
Слайд 8Принятие решений после построения линейной модели
Модель: адекватна неадекватна
(увеличение
точности)
линейна нелинейна
(планы 2-го
порядка)
Коэф-ты: значимы незначимы
1) узкие интервалы варьирования
2) большая ошибка эксперимента
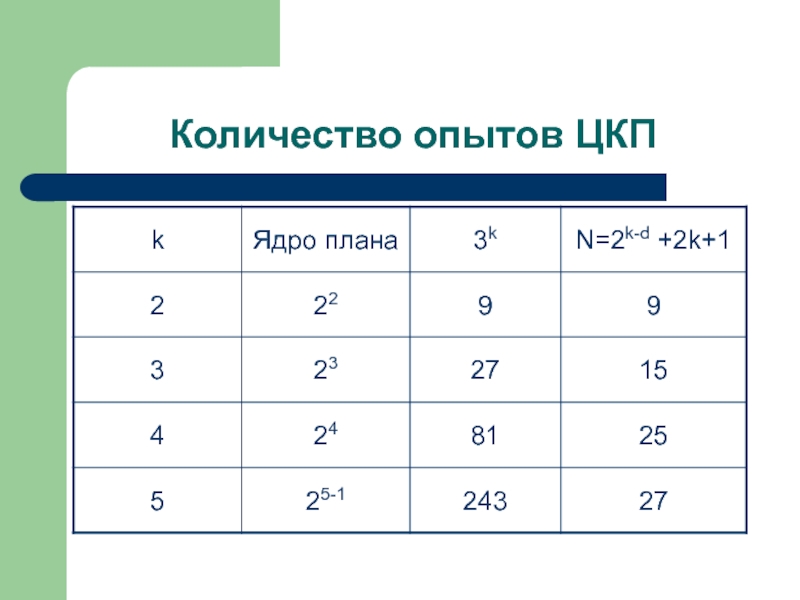
Слайд 9Планы второго порядка
Уравнение второго порядка
ПФЭ
Слайд 10Планы второго порядка
Уравнение второго порядка
ПФЭ Центральный композиционный план
Опыты из планир-я 1-го порядка
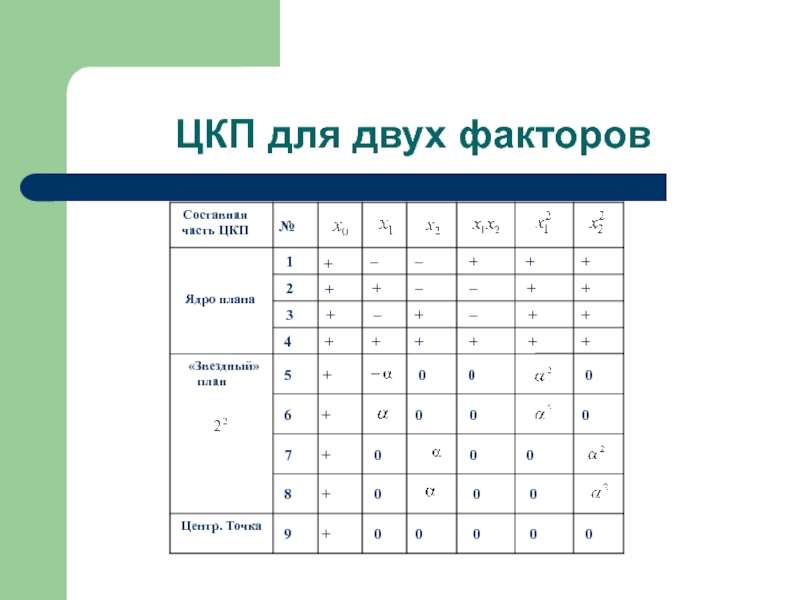
Слайд 11Центральный композиционный план (ЦКП) для двух факторов
5 уровней:
-α
-1 0 +1 +α
Слайд 12–
0
0
0
0
0
+
9
Центр. Точка
0
0
0
+
8
0
0
0
+
7
0
0
0
+
6
0
0
0
+
5
«Звездный» план
+
+
+
+
+
+
4
+
+
–
+
–
+
3
+
+
–
–
+
2
+
+
+
–
1
№
Составная часть ЦКП
ЦКП для двух факторов
Ядро плана
+
+
Слайд 14Выбор «звездного» плеча
(для ортогонального планирования)
Слайд 15Расчет коэффициентов
Пусть b0 b1 b2 b3 b12=b4 b13=b5 b23=b6 b11=b7
…
Слайд 16Дисперсии оценивания
где – выборочная дисперсия
Слайд 17Проверка значимости коэффициентов
Критерий Стьюдента:
Коэффициент значим, если
Слайд 18Задача оценки точности
Задача 1: оценка точности и достоверности при заданном
методе реализации модели, при заданном объеме выборки;
Задача 2: оценка необходимого
числа реализаций при заданных точности и достоверности результатов.
Желаемую степень точности можно задавать:
а) в виде доли стандартного отклонения;
б) в процентах от величины среднего значения;
в) в абсолютных величинах.
Слайд 19Оценивание среднего значения совокупности (задача 2)
Задача: необходимо построить такую оценку
истинного среднего значения совокупности, что
где — выборочное среднее,
— вероятность
того, что интервал
содержит
Необходимый для этого условия объем выборки:
где — двусторонняя стандартная нормальная статистика (допустимая величина риска);
— допустимая разность между оценкой и истинным значением
параметра;
— величина изменчивости совокупности,
Слайд 20Оценивание среднего значения совокупности (задача 1)
Задача: какой точности d мы
достигнем при заданном объеме выборки n?
Достигаемая точность:
где — выборочная дисперсия,
полученная на выборке n;
— критерий Стьюдента
Слайд 21Пример. Оценка точности
- неизвестна.
Точность в долях стандартного отклонения:
Необходимый
для этого условия объем выборки:
Слайд 22Оценивание дисперсии совокупности
Задача: построение доверительных интервалов
где
— число, характеризующее степень близости оценки
к истинной
дисперсии .
Необходимый для этого условия объем выборки:
Слайд 23Сравнение двух распределений
Задача: проверка близости распределения отклика модели к некоторому
другому распределению.
Под желаемой точностью будем понимать
максимальную разность сравниваемых распределений во всех точках
Необходимый для этого условия объем выборки:
где — табличное значение функции Колмогорова.
Слайд 24Стратегическое и тактическое планирование
Стратегическое планирование (первая составляющая планирования экспериментов с
моделями систем) ставит целью решение задачи получения необходимой информации о
системе с помощью модели, с учетом ограничения на ресурсы.
Тактическое планирование (вторая составляющая) — это определение способа проведения каждой серии испытаний модели, предусмотренных планом эксперимента.
Слайд 25Некоторые проблемы стратегического планирования
сложность построения плана эксперимента;
наличие большого количества факторов;
многокомпонентность
функции отклика;
ограниченность ресурсов проведения эксперимента.
Слайд 26Этапы стратегического планирования
построение структурной модели осуществляется исходя из того, что
должно быть сделано;
построение функциональной модели производится исходя из того, что
может быть сделано.
Слайд 27Структурная модель
Структурная модель плана эксперимента характеризуется числом факторов и числом
уровней для каждого фактора.
Число элементов эксперимента ,
где
— число факторов эксперимента;
— число уровней i-го фактора.
Число уровней зависит от предполагаемой функциональной зависимости между откликом и факторами.
Если уровни равноотстоят друг от друга и если
для всех факторов, то получаем ПФЭ -го порядка.
Слайд 28Функциональная модель
Функциональная модель определяет количество необходимых элементов структурной модели .
Модель полная, если (ПФЭ),
Модель неполная, если
(ДФЭ).
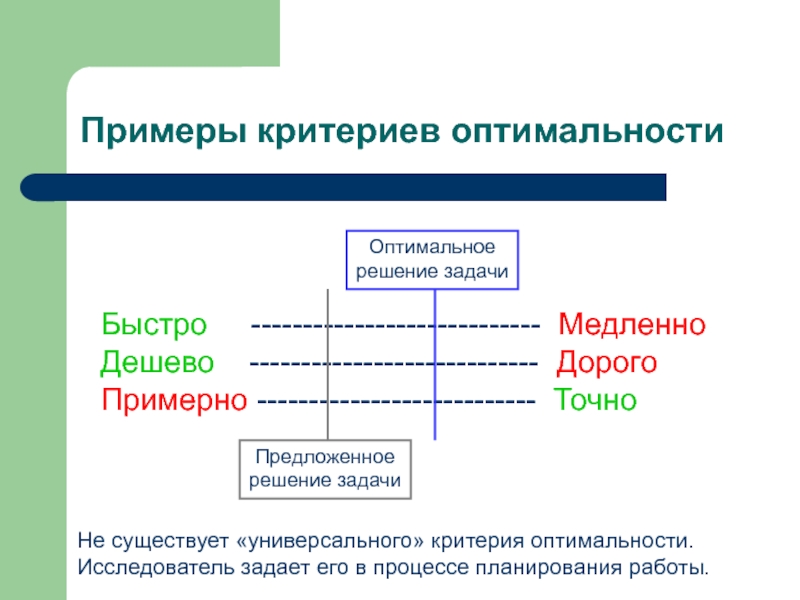
Слайд 29Примеры критериев оптимальности
Быстро ---------------------------- Медленно
Дешево ---------------------------- Дорого
Примерно
--------------------------- Точно
Предложенное
решение задачи
Оптимальное
решение задачи
Не существует «универсального» критерия оптимальности.
Исследователь
задает его в процессе планирования работы.
Слайд 30Выбор критерия оптимальности
Если для каждого из экспериментов, приводящих к желаемому
результату, можно оценить величину «затрат», то задача заключается в выборе
такого эксперимента, при котором «затраты» минимальны.
«Стоимостный» подход возможен только в том случае, когда все эксперименты приводят к одинаковой точности результата.
Слайд 31Подбор компонентов функциональной модели
Можно варьировать: количество факторов ,
число уровней ,
количество повторений эксперимента .
Учитываются: затраты времени на 1 опыт ,
стоимость опыта .
Полное число опытов при симметрично повторяемом эксперименте:
Общее время, требуемое для проведение эксперимента:
Общие затраты:
Слайд 32Пример. Стратегия поездки из пункта А в пункт Б
Из пункта
А в пункт Б можно попасть разными путями, за разное
время, затратив разное количество денег (горючее, амортизация а/м, штрафы, заработок за счет попутных пассажиров). Каждый водитель формирует свой критерий оптимальности, например:
Экономия денег (аккуратная езда, выбор оптимальной скорости, соблюдение правил, подбор попутчиков) за счет времени;
Экономия времени (быстрая езда) за счет денег (штрафы, без попутчиков, повышенный износ автомашины), безопасности, душевного спокойствия и комфорта (тряска, рывки).
Повышение безопасности за счет времени;
Сохранение душевного спокойствия (избегание улиц с интенсивным движением, строгое выполнение правил) за счет времени и денег (более длинный путь).



































![Автоматизация звука [ ж ].
Артикуляционная гимнастика
Звук [ ж ]
Звук [ ж ] в](/img/thumbs/59024895a4c1d926498e9f6ee904cc8b-800x.jpg)