Слайд 1ПЛОСКАЯ ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ
Кафедра теоретической механики и сопротивления материалов
Методические указания
для практических занятий по теоретической механике
Владивосток
2009
Составил В. Г. Непейвода
ФЕДЕРАЛЬНОЕ АГЕНТСТВО
МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Морской государственный университет им. адм. Г. И. Невельского
Слайд 2 Содержание
1. Основные понятия и определения в вопросах
и ответах
2. Момент пары сил
3. Примеры
решения задач
4. Задачи для самостоятельного решения
Слайд 3
1. Основные понятия в вопросах и ответах
1.
Какая система сил называется плоской произвольной?
Плоской произвольной называется
система сил, у которой линии действия сил лежат произвольно в одной плоскости,
рис. 1
Слайд 4 2. К каким векторным величинам приводится плоская произ-вольная
система сил?
Слайд 5 3. Как направлены относительно друг друга главный вектор
и главный момент плоской произвольной системы сил?
Главный
вектор плоской произвольной системы сил лежит в плоскости действия сил, а главный момент перпендикулярен плоскости действия сил, рис. 2.
Слайд 6 4. Какие условия выполняются при равновесии тела под
действием плоской произвольной системы сил?
Для равновесия плоской произвольной
системы сил необходимо и достаточно, чтобы главный вектор и главный момент этой системы сил относительно произвольного центра равнялись нулю.
Слайд 7 5. Какие уравнения равновесия можно составить для плоской
произвольной системы сил?
Из условий равновесия плоской произвольной системы
сил можно получить уравнения равновесия в трёх различных формах:
Слайд 8
6. Какие уравнения равновесия чаще всего используются на
практике?
При использовании уравнений равновесия плоской произвольной системы сил
надо иметь в виду, что оси х, у в форме а) располагаются произвольно, но, как правило, используются взаимно-перпендикулярные оси;
На практике чаще всего используются уравнения в форме а).
Слайд 9точки А и В в форме б) произвольны и АВ
не перпендикулярна оси Оx;
Слайд 10 точки А, В и С в форме в)
не лежат на одной прямой.
Слайд 11 7. Что характеризует момент силы относительно точки?
Момент силы относительно точки (полюса, центра) – это физическая
величина, характеризующая меру вращательной способности данной силы относительно точки (полюса, центра).
8. Что называется плечом силы относительно точки?
Плечом силы относительно точки называют расстояние от точки до линии действия силы. (Расстояние от точки до линии действия силы – это длина перпендикуляра, опущенного из точки на линию действия силы.)
9. Чему равен момент силы относительно точки?
Для сил, лежащих в одной плоскости, момент каждой силы относительно выбранной точки на этой плоскости равен произведению модуля силы на её плечо, взятому со знаком «плюс» или «минус».
Слайд 12 10. Какое правило знаков применяется для моментов сил
относительно точки?
Установлено следующее правило для моментов сил: моменту
присваивается знак «+», если сила стремится вращать тело относительно данной точки против хода часовой стрелки, в противном случае присваивается знак «−».
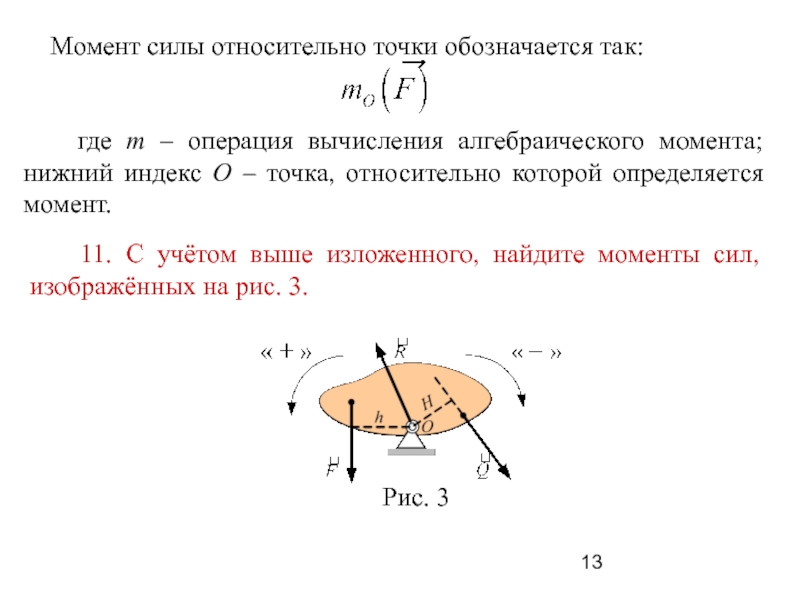
Слайд 13 Момент силы относительно точки обозначается так:
где m – операция вычисления алгебраического момента; нижний индекс О
– точка, относительно которой определяется момент.
11. С учётом выше изложенного, найдите моменты сил, изображённых на рис. 3.
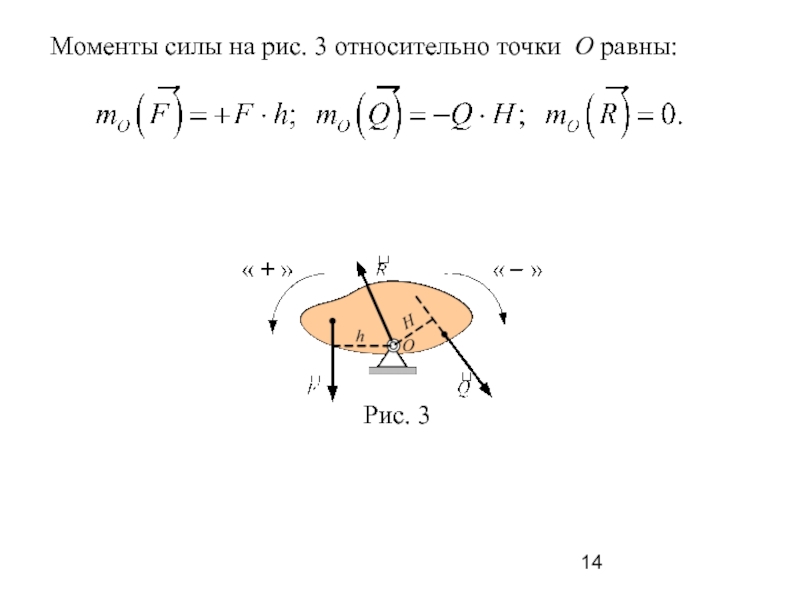
Слайд 14
Моменты силы на рис. 3 относительно точки О
равны:
Слайд 17
Во многих случаях момент силы удобнее определять, применяя
теорему Вариньона. Согласно этой теореме момент любой силы относительно какой-либо
точки равен алгебраической сумме моментов составляющих этой силы относительно той же точки.
13. Как формулируется теорема Вариньона?
Слайд 18 Порядок применения теоремы Вариньона для определения момента произвольной
силы относительно центра О следую-щий:
1) разложить вектор силы
по двум направлениям (обычно взаимно-перпендикулярным), вдоль принятых координатных осей;
2) определить момент данной силы относительно точки как алгебраическую сумму моментов составляющих:
Слайд 20
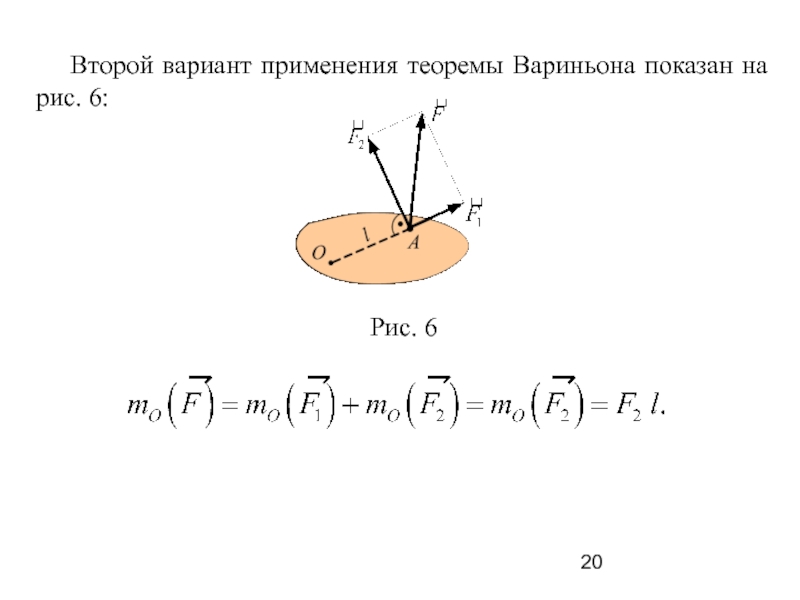
Второй вариант применения теоремы Вариньона показан на рис.
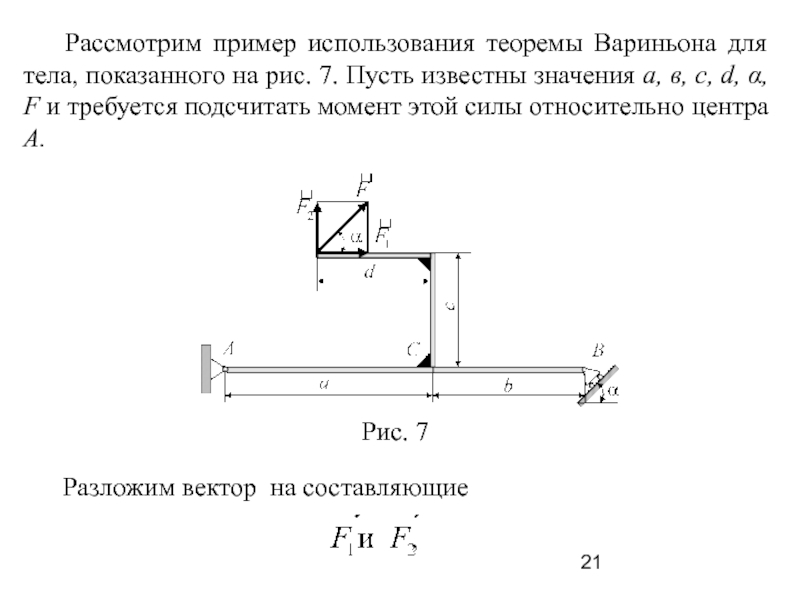
Слайд 21 Рассмотрим пример использования теоремы Вариньона для тела, показанного
на рис. 7. Пусть известны значения а, в, с, d,
α, F и требуется подсчитать момент этой силы относительно центра А.
Разложим вектор на составляющие
Слайд 22
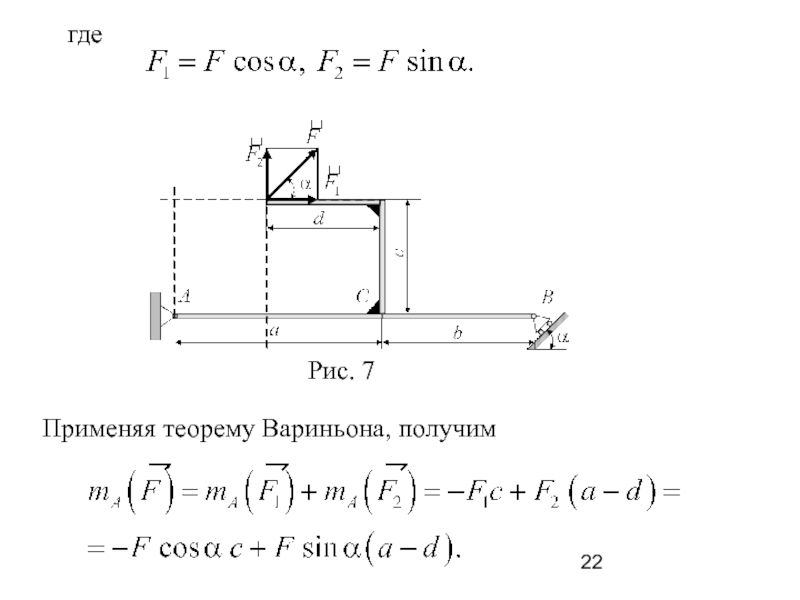
где
Применяя теорему Вариньона, получим
Слайд 232. Момент пары сил
Парой сил называется совокупность
двух численно равных, направленных в противоположные стороны сил, линии дей-ствия
которых параллельны. Очевидно, что главный вектор пары сил равен нулю. Поэтому пара сил не даёт слагаемых в уравнения проекций. Она учитывается только в уравнении моментов. На чертеже изображение пары Вы можете встретить в одном из следующих видов, рис. 8:
Если рассматриваемое тело – абсолютно твёрдое, то точка приложения пары сил не имеет значения: её момент относительно любой точки в плоскости действия пары будет иметь одно и то же алгебраическое значение.
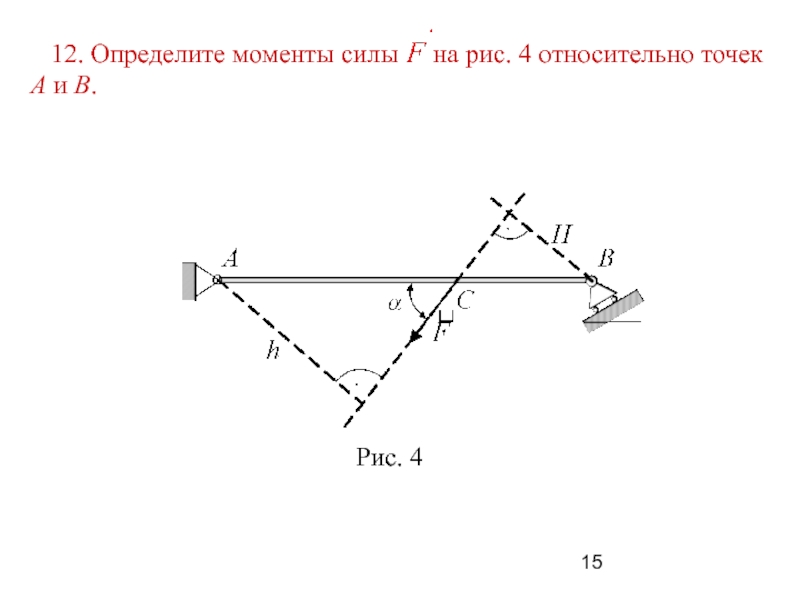
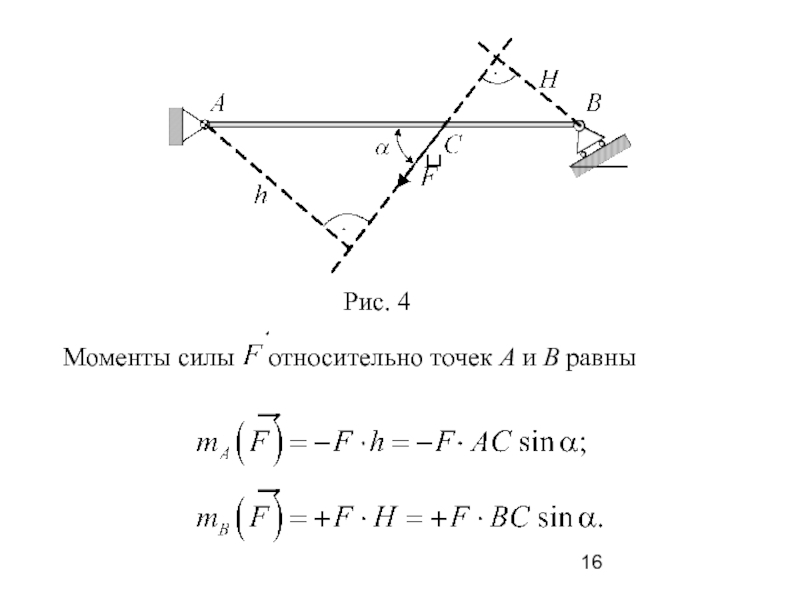
Слайд 243. Примеры решения задач
Пример 1. Невесомая горизонтальная балка
АВ (рис. 9) опирается в точке А на цилиндрический шарнир,
в точке В – на ломаный невесомый стержень ВСD. К балке приложены: пара сил с моментом m и в точке Е сосредоточенная сила F.
Определить реакции связей, наложенных на балку, если АВ = 3 м; АЕ = ЕВ; ВС = СD; m = 5 кН м; F = 6 кН; α = 60o.
Слайд 25 1. Запишем краткое условие задачи.
Дано: F = 6
кН; m = 5 кН м; АВ = 3 м;
АЕ = ЕВ; ВС = СD;
α = 60°.
Определить: RA, RB.
Слайд 26 2. Составим расчётную схему к задаче в следующей
последовательности:
1) рассмотрим равновесие балки АВ. Отбросим действующие на
балку связи и изобразим её на рисунке;
2) покажем действующие на балку активные силы: силу F и пару сил с моментом m;
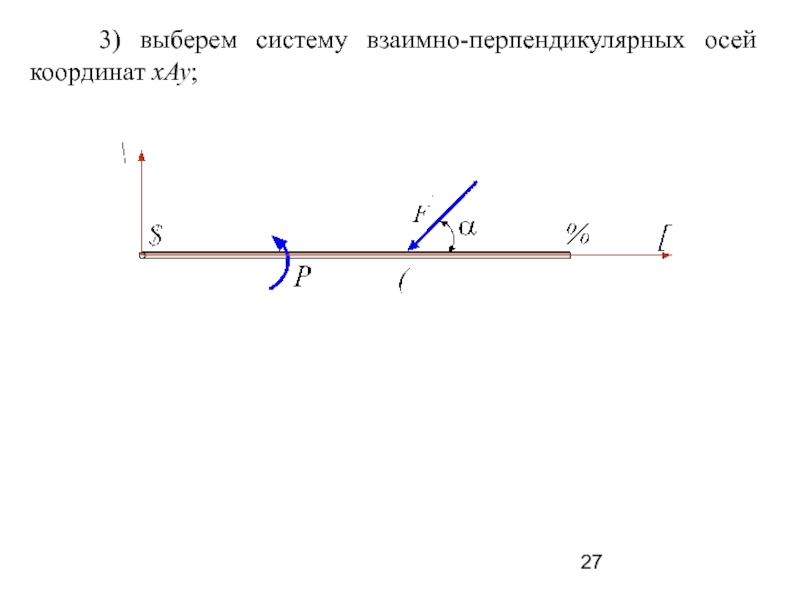
Слайд 27 3) выберем систему взаимно-перпендикулярных осей координат xAy;
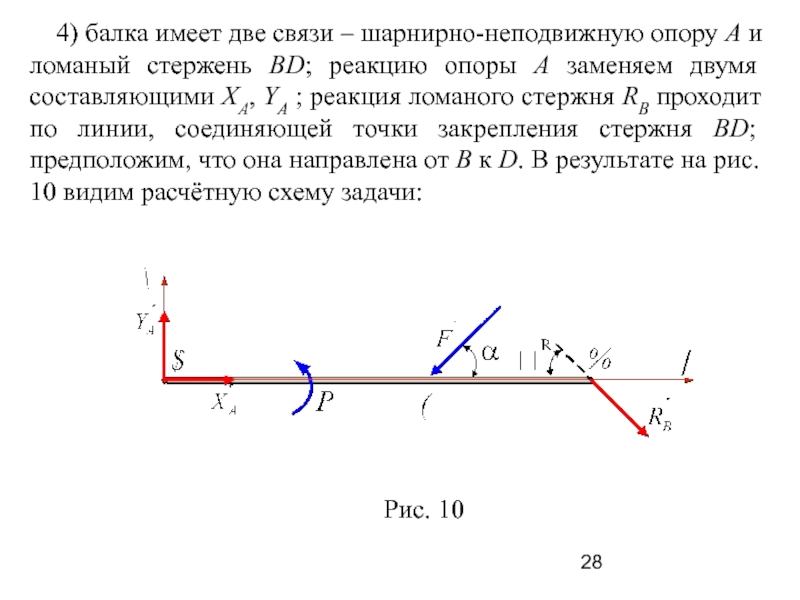
Слайд 28 4) балка имеет две связи – шарнирно-неподвижную опору
А и ломаный стержень BD; реакцию опоры А заменяем двумя
составляющими XA, YA ; реакция ломаного стержня RB проходит по линии, соединяющей точки закрепления стержня BD; предположим, что она направлена от В к D. В результате на рис. 10 видим расчётную схему задачи:
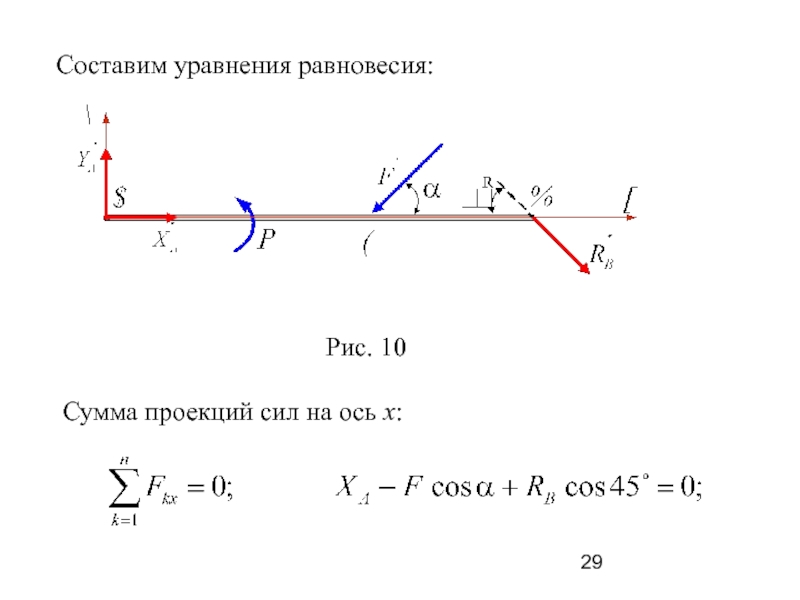
Слайд 29 Составим уравнения равновесия:
Сумма проекций сил на
ось x:
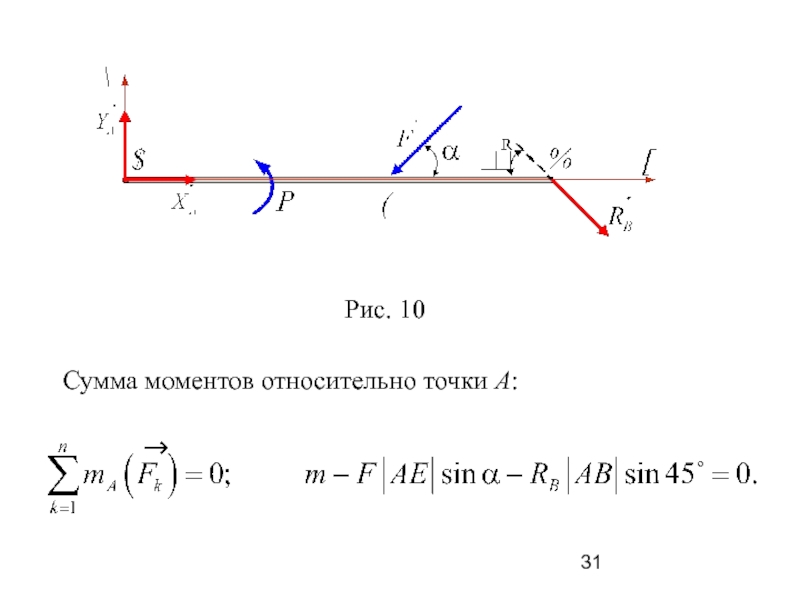
Слайд 31 Сумма моментов относительно точки А:
ХА – 6⋅0,5 + RB⋅0,707 = 0,
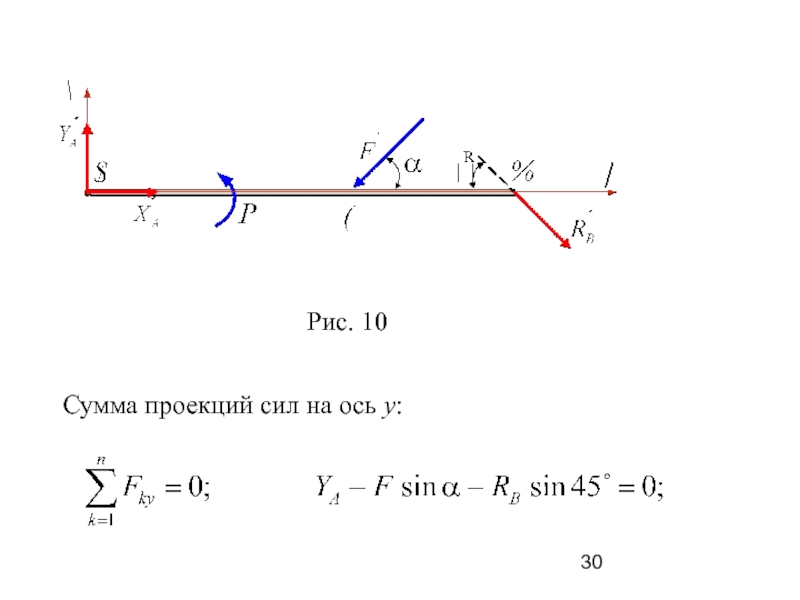
YА – 6⋅0,866 – RВ⋅0,707 = 0,
5 – 6⋅1,5⋅0,866 – RB⋅3⋅0,707 = 0,
Подставляя в уравнения равновесия данные из условия задачи, находим неизвестные реакции:
ХА = 3,93 кН; YА = 4,27 кН; RB = –1,32 кН.
Слайд 33 Для проверки результатов решения составим ещё одно уравнение
моментов относительно произвольной точки С, по отношению к которой все
найденные реакции опор балки дают моменты, отличные от нуля. Выберем точку С с координатами: xС = yС = 1 м.
Слайд 34 Тогда:
что подтверждает правильность решения задачи.
Слайд 35 Пример 2. Пренебрегая весом крана АСD, определить реакции
подпятника А и подшипника В, возникающие при равномерном подъёме груза
Р, рис. 11.
1. Запишем краткое условие задачи и выполним рисунок к задаче.
Дано: Р, α, АВ = a, ВС = в, CD = с. Определить: XA, YA, RB.
Решение
Слайд 36 2. Составим расчётную схему в следующей последователь-ности:
1) рассмотрим равновесие крана; изобразим его на
рис. 12;
Слайд 37 2) покажем действующие на кран силу P,
которая равна по величине весу груза, прикреплённого к тросу, перекинутому
через блок Е;
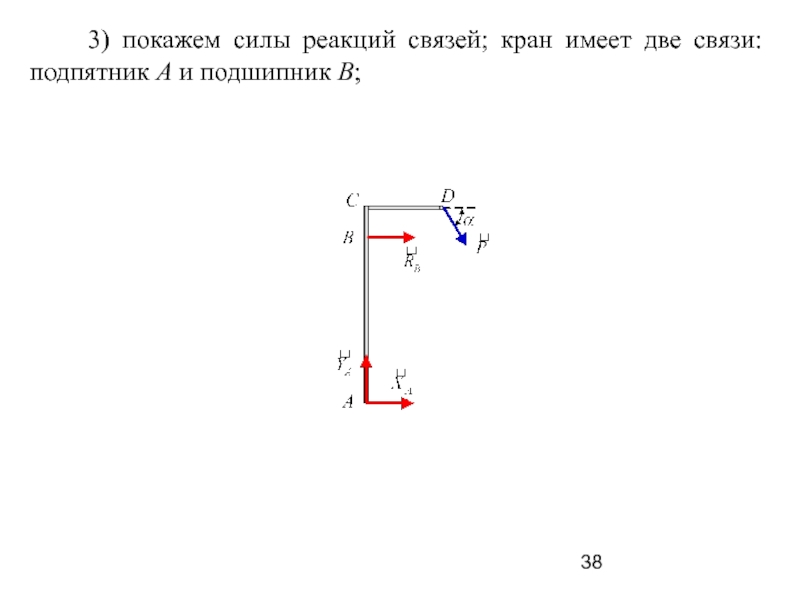
Слайд 38 3) покажем силы реакций связей; кран имеет
две связи: подпятник А и подшипник В;
Слайд 39 3. Построим координатные оси xAy.
В результате на рис. 12 получим расчётную схему, построен-ную
с применением метода освобождения от связей.
Слайд 40 4. Составим уравнения равновесия:
Сумма
проекций сил на ось x:
Слайд 42 Сумма моментов сил относительно точки А:
Слайд 43 Из этих уравнений определим реакции:
Слайд 44 Для проверки предлагаем составить уравнение:
Если в уравнении не
будет ошибок, то оно будет удовлетво-ряться тождественно.
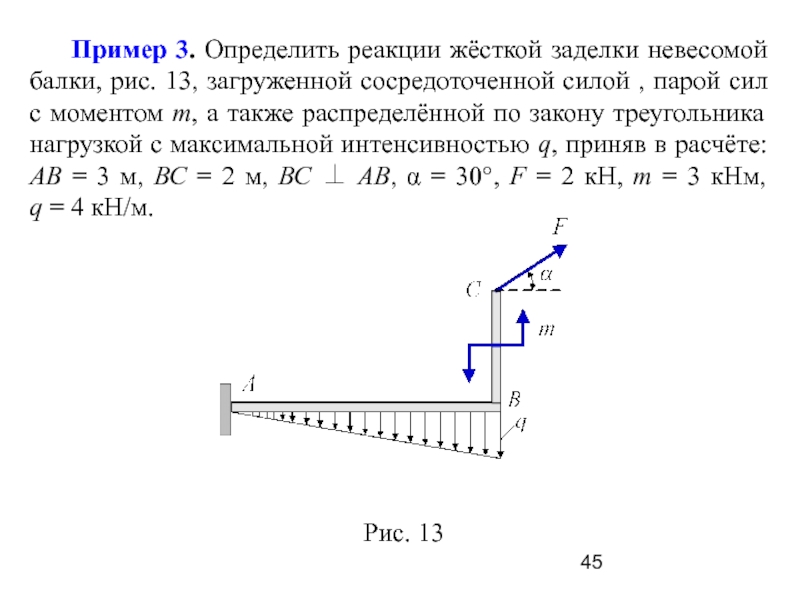
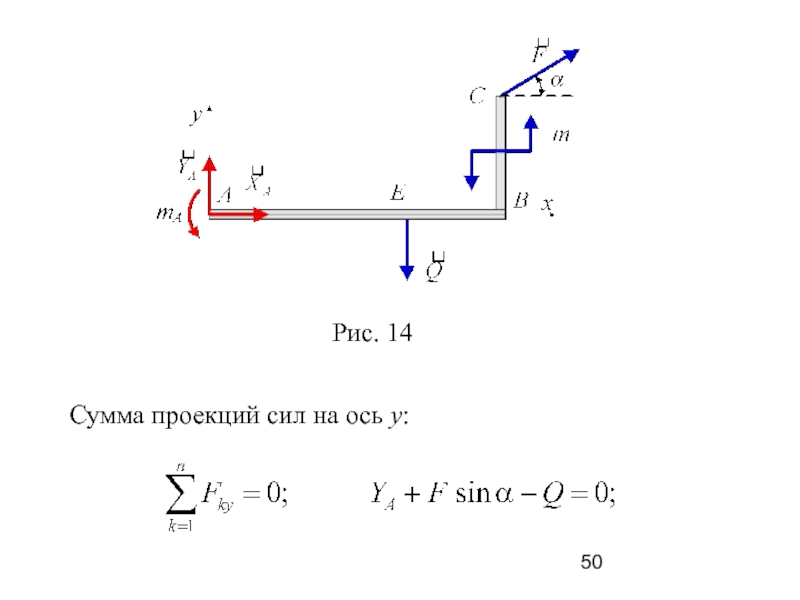
Слайд 45 Пример 3. Определить реакции жёсткой заделки невесомой
балки, рис. 13, загруженной сосредоточенной силой , парой сил с
моментом m, а также распределённой по закону треугольника нагрузкой с максимальной интенсивностью q, приняв в расчёте: АВ = 3 м, ВС = 2 м, ВС ⊥ АВ, α = 30°, F = 2 кН, m = 3 кНм,
q = 4 кН/м.
Слайд 46 2. Составим расчётную схему в следующей последователь-ности:
1) чтобы определить силы реакций, рассмотрим равновесие балки; выполним рисунок
балки, отбросив заделку;
Слайд 47
линия действия силы делит катет АВ прямоугольного треу-гольника в точке
Е на отрезки:
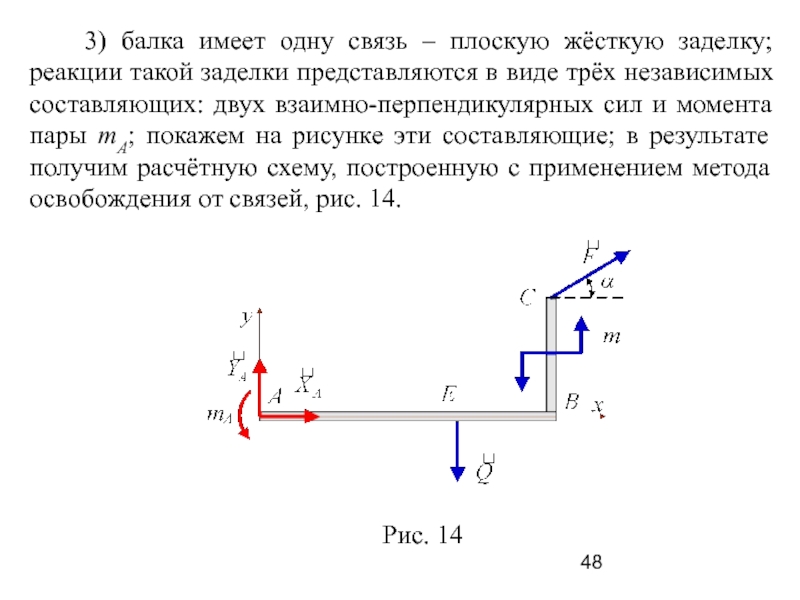
Слайд 48 3) балка имеет одну связь – плоскую жёсткую
заделку; реакции такой заделки представляются в виде трёх независимых составляющих:
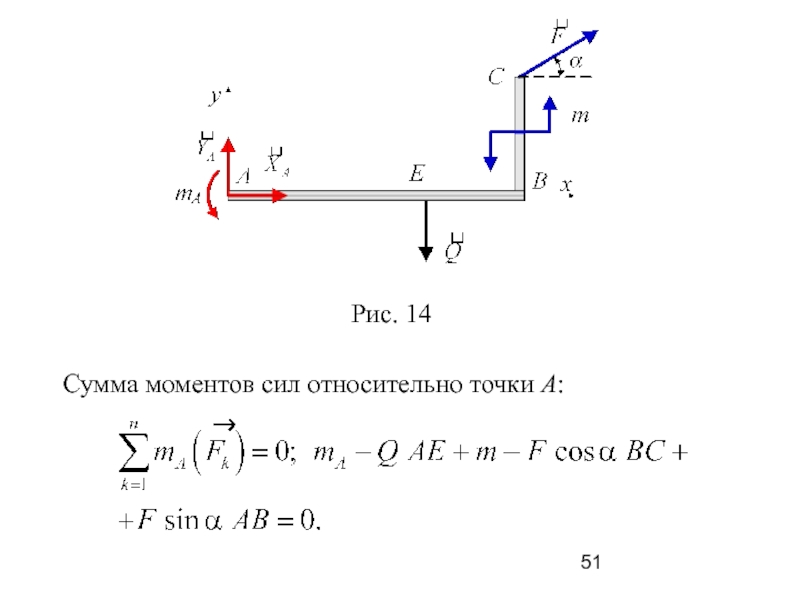
двух взаимно-перпендикулярных сил и момента пары mA; покажем на рисунке эти составляющие; в результате получим расчётную схему, построенную с применением метода освобождения от связей, рис. 14.
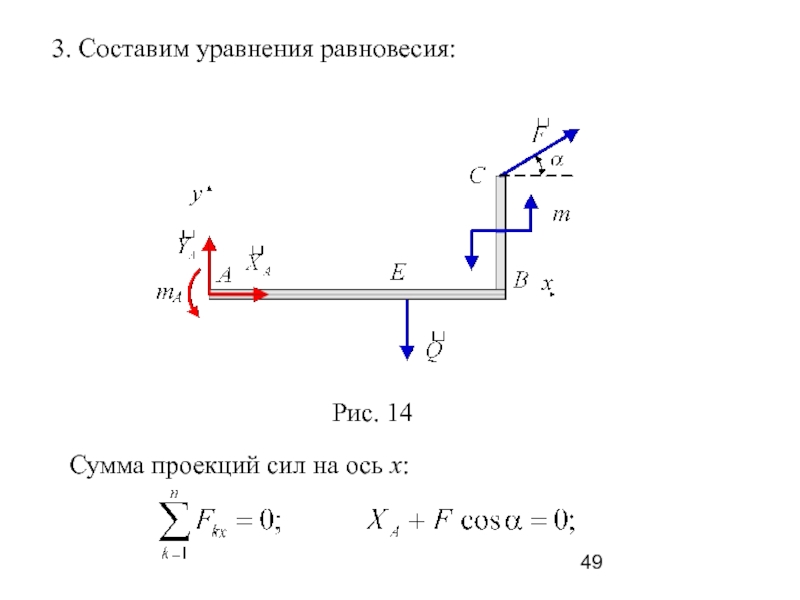
Слайд 49 Сумма проекций сил на ось x:
3. Составим уравнения равновесия:
Слайд 51 Сумма моментов сил относительно точки А:
Слайд 52 Получили систему уравнений:
Решим эту
систему уравнений, используя пакет Mathcad.
Дано:
Слайд 54 Ответ:
Для проверки результатов решения составили
уравнение:
Уравнение тождественно удовлетворится. Следовательно, в решении нет
ошибок.
Слайд 55 В результате решения уравнений получили:
ХА= – 1,73 кН;
YА = 5,00 кН; mА = 9,46 кНм.
Слайд 564. Задачи для самостоятельного решения
1. Однородная балка АВ
весом Р = 100 Н прикреплена к стене шарниром А
и удерживается под углом 45o к вертикали при помощи троса, перекинутого через блок С и несущего груз G. Ветвь ВС троса образует с вертикалью угол 30o. В точке D к балке подвешен груз Q весом 200 Н, рис. 15. Определить вес груза G и реакцию шарнира А, пренебрегая трением на блоке, если ВD =BA/4.
Ответ:
G = 146,38 H;
XA = 73,19 H;
YA = 173,24 H.
Слайд 57 2. Однородный стержень АВ весом 100 Н опирается
одним концом на гладкий горизонтальный пол, другим – на гладкую
плоскость, наклонённую под углом 30° к горизонту. У конца В стержень поддерживается верёвкой, перекинутой через блок С и несущей груз Р, часть верёвки ВС параллельна наклонной плос-кости, рис. 16.
Пренебрегая трением на блоке, определить величину груза Р и силы давления NА и NВ на пол и на наклонную плоскость.
Ответ:
P = 25 H;
NA = 50 H;
NB = 43,3 H.
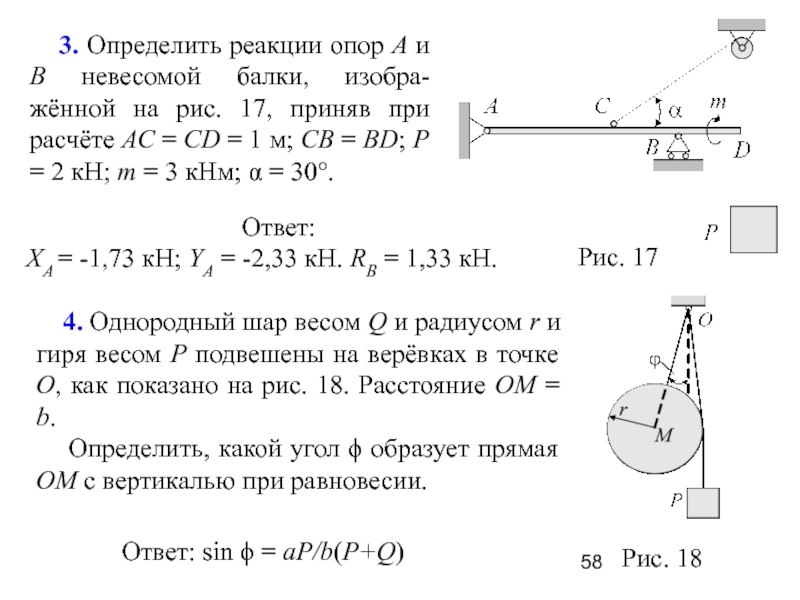
Слайд 58 3. Определить реакции опор А и В невесомой
балки, изобра-жённой на рис. 17, приняв при расчёте АС =
CD = 1 м; СВ = ВD; Р = 2 кН; m = 3 кНм; α = 30°.
4. Однородный шар весом Q и радиусом r и гиря весом Р подвешены на верёвках в точке О, как показано на рис. 18. Расстояние ОМ = b.
Определить, какой угол ϕ образует прямая ОМ с вертикалью при равновесии.
Ответ:
XA = -1,73 кH; YA = -2,33 кH. RB = 1,33 кH.
Ответ: sin ϕ = aP/b(P+Q)
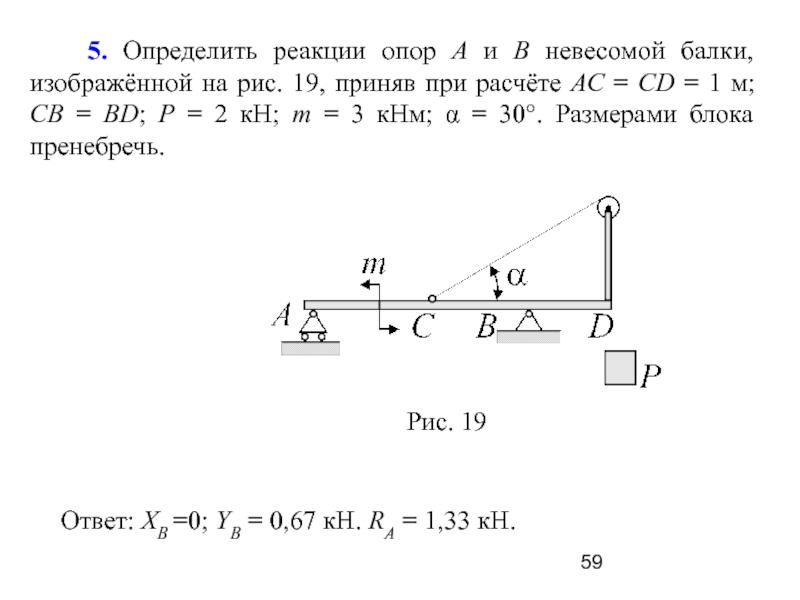
Слайд 59 5. Определить реакции опор А и В невесомой
балки, изображённой на рис. 19, приняв при расчёте АС =
CD = 1 м; СВ = BD; Р = 2 кН; m = 3 кНм; α = 30°. Размерами блока пренебречь.
Ответ: XB =0; YB = 0,67 кH. RA = 1,33 кH.
Слайд 60 6. Ломаный рычаг АВС, имеющий неподвижную ось В,
весом P = 80 Н; плечо АВ = 0,4 м,
плечо ВС = 1 м, центр тяжести рычага находится на расстоянии 0,212 м от вертикаль-ной прямой ВD. В точках А и С привязаны верёвки, перекинутые через блоки Е и К и натягиваемые гирями весом Р1 = 310 Н и Р2 = 100 Н, рис. 20.
Пренебрегая трением на блоках, определить угол ВСК = α в положении равновесия, если угол ВАЕ = 135°.
Ответ: α1 =45o; α2 = 135o.
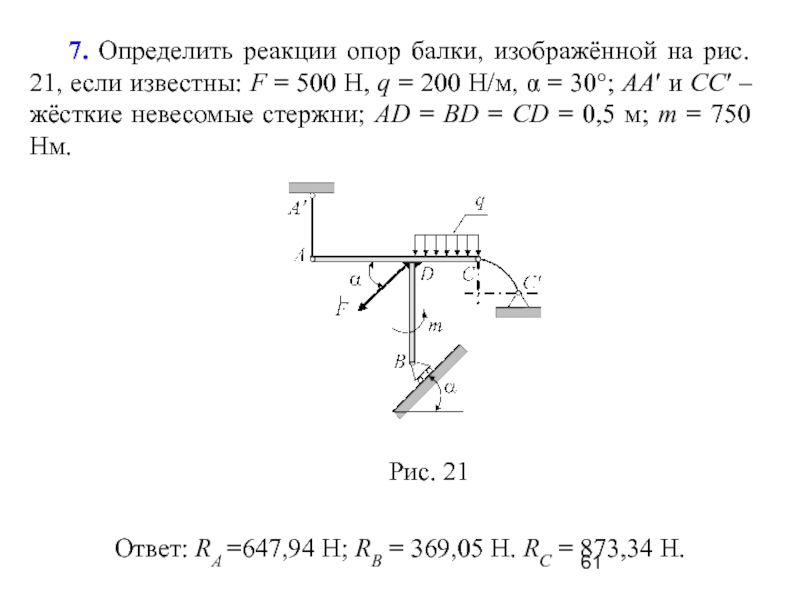
Слайд 61 7. Определить реакции опор балки, изображённой на рис.
21, если известны: F = 500 Н, q = 200
Н/м, α = 30°; АА′ и СС′ – жёсткие невесомые стержни; АD = BD = CD = 0,5 м; m = 750 Нм.
Ответ: RA =647,94 H; RB = 369,05 H. RC = 873,34 H.
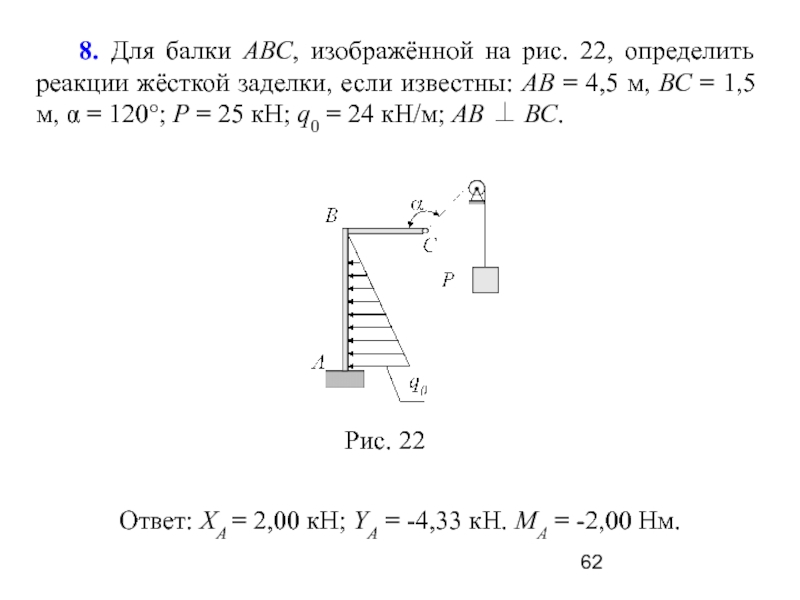
Слайд 62 8. Для балки АВС, изображённой на рис. 22,
определить реакции жёсткой заделки, если известны: АВ = 4,5 м,
ВС = 1,5 м, α = 120°; Р = 25 кН; q0 = 24 кН/м; АВ ⊥ ВС.
Ответ: XA = 2,00 кH; YA = -4,33 кH. MA = -2,00 Hм.
Слайд 63 9. Определить реакции опор А и В двухконсольной
балки, находящейся под действием сосредоточенной силы Р, пары сил с
моментом m и распределённой нагрузки, изменяющейся по закону треугольника, рис. 23. В расчёте принять: Р = 2 кН, m = 3 кНм, q0 = 3 кН/м: А1А = АВ = ВВ1 = 0,6 м; α = 60°.
Ответ: XA = 1,00 кH; YA = 2,60 кH. RB = 4,33 кH.
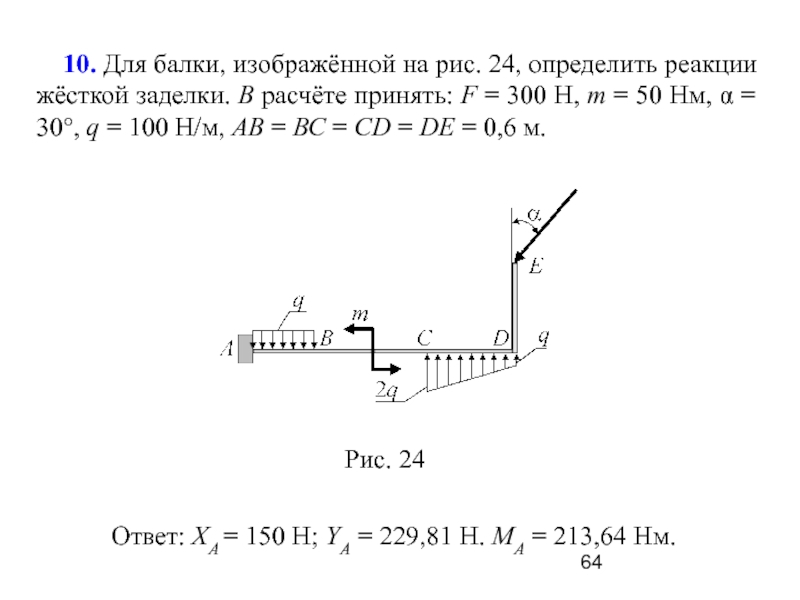
Слайд 64 10. Для балки, изображённой на рис. 24, определить
реакции жёсткой заделки. В расчёте принять: F = 300 H,
m = 50 Hм, α = 30°, q = 100 Н/м, АВ = ВС = CD = DE = 0,6 м.
Ответ: XA = 150 H; YA = 229,81 H. MA = 213,64 Hм.
Слайд 66 2. Выполнить то же, что и в п.
1, при действии только силы F ;
3. Выполнить
то же, что и в п. 1, при действии только пары сил с моментом m.