Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
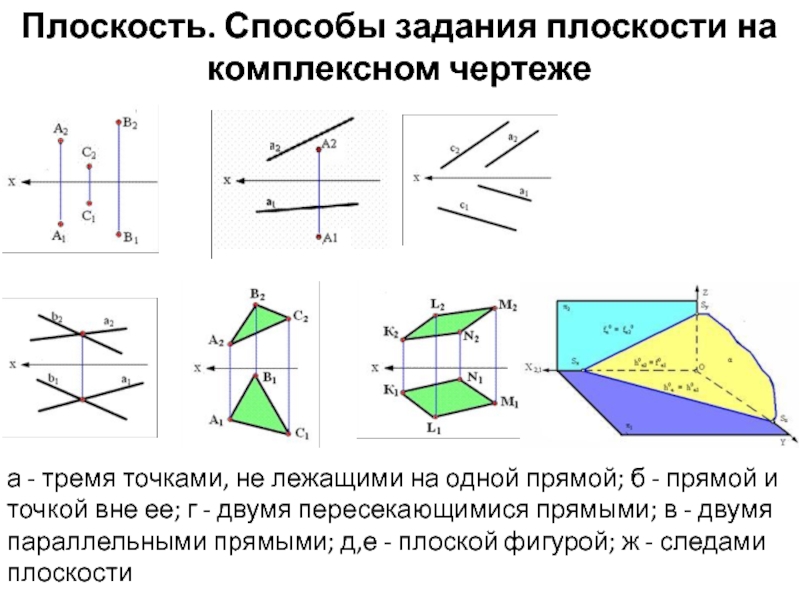
Плоскость. Способы задания плоскости на комплексном чертеже а - тремя точками,
Содержание
- 1. Плоскость. Способы задания плоскости на комплексном чертеже а - тремя точками,
- 2. Общее и частные положения плоскости в пространствеПлоскость,
- 3. Плоскости, перпендикулярные плоскостям проекций (проецирующие плоскости) Плоскость, перпендикулярная
- 4. Основным свойством фронтально-проецирующей плоскости является то, что
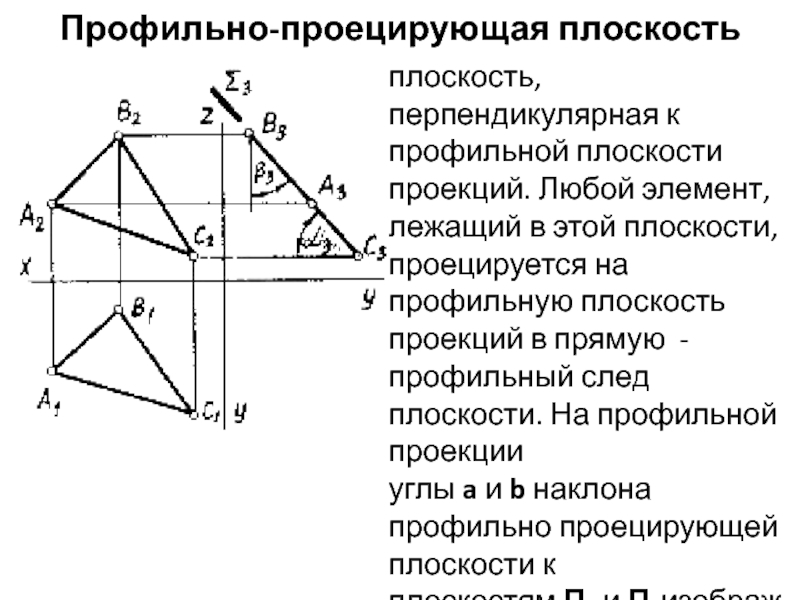
- 5. Профильно-проецирующая плоскостьплоскость, перпендикулярная к профильной плоскости проекций.
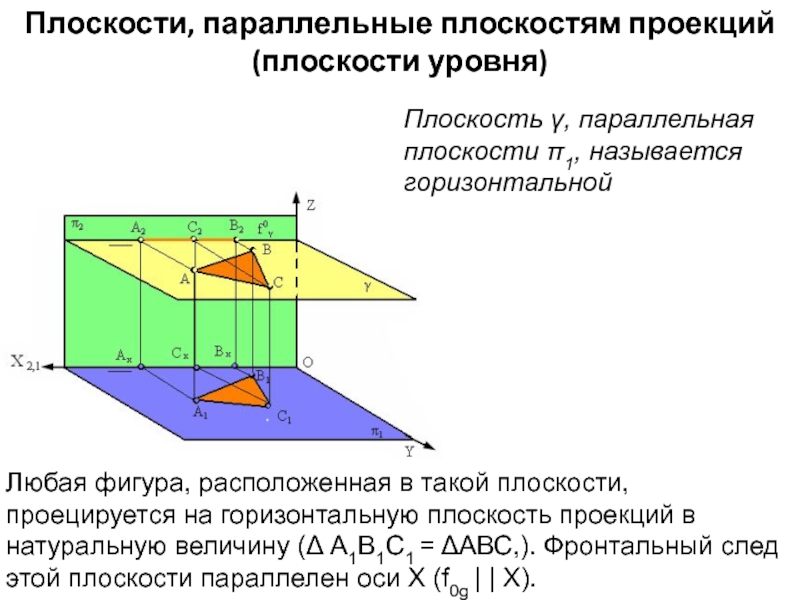
- 6. Плоскости, параллельные плоскостям проекций(плоскости уровня)Плоскость γ, параллельная
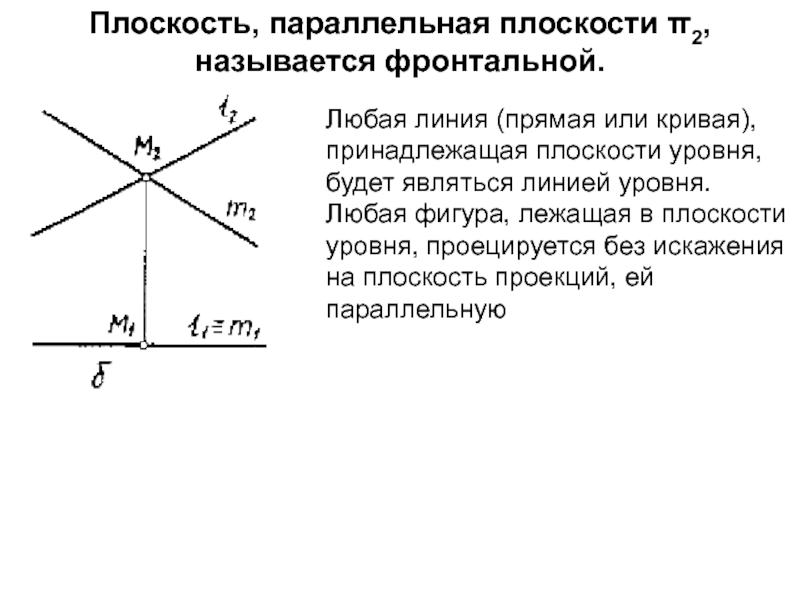
- 7. Плоскость, параллельная плоскости π2, называется фронтальной.Любая линия
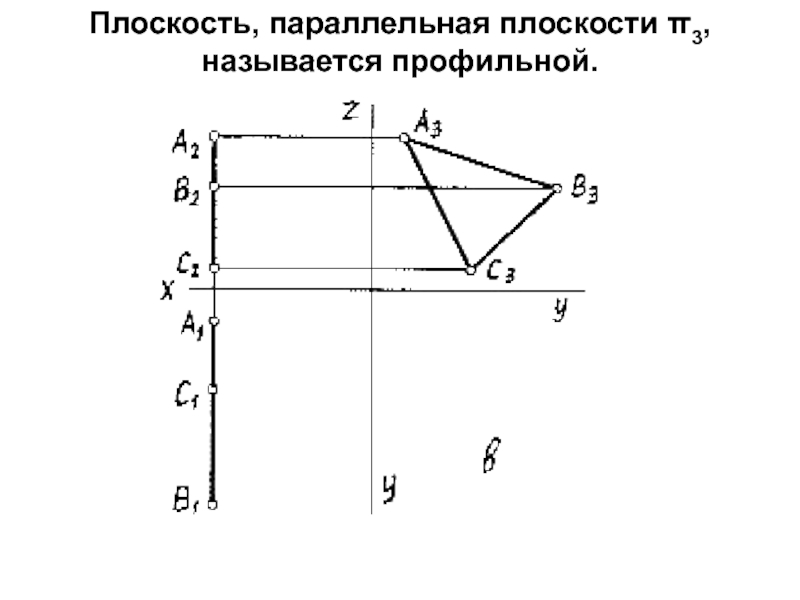
- 8. Плоскость, параллельная плоскости π3, называется профильной.
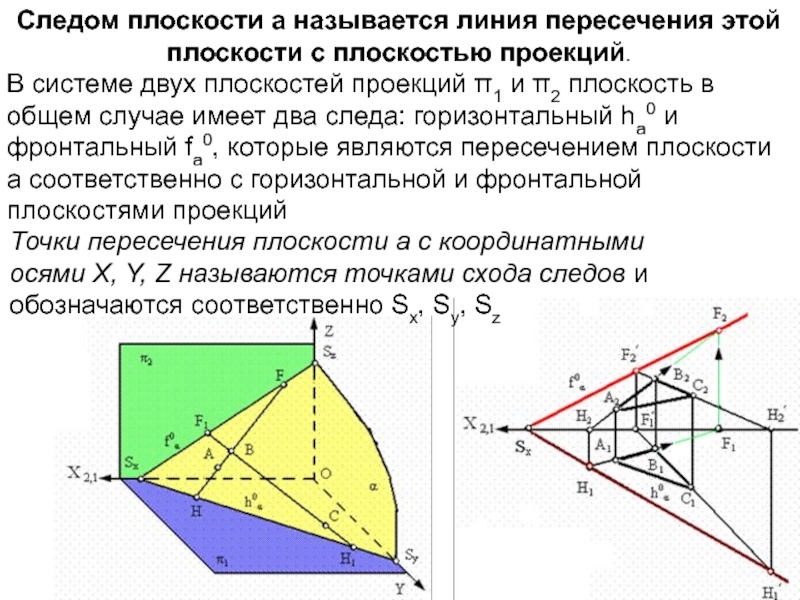
- 9. Следом плоскости a называется линия пересечения этой плоскости с
- 10. Прямая и точка в плоскости Прямая
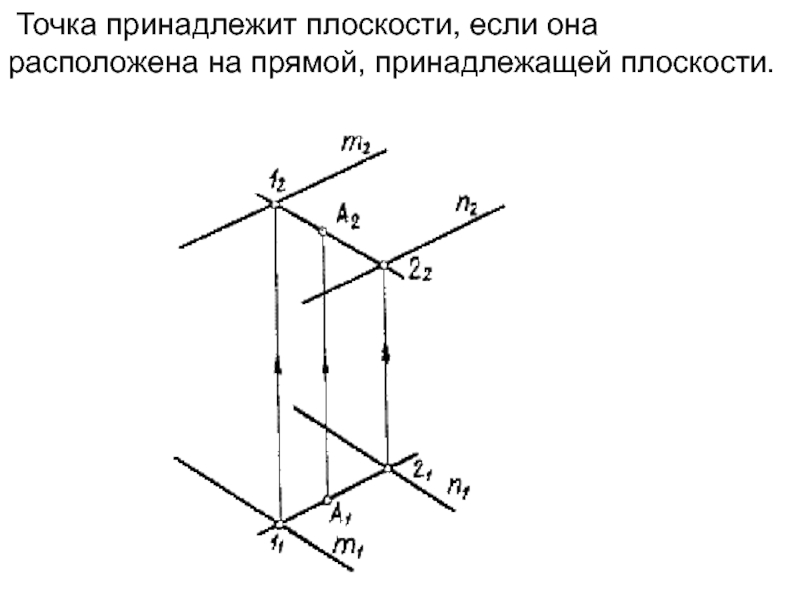
- 11. Точка принадлежит плоскости, если она расположена на прямой, принадлежащей плоскости.
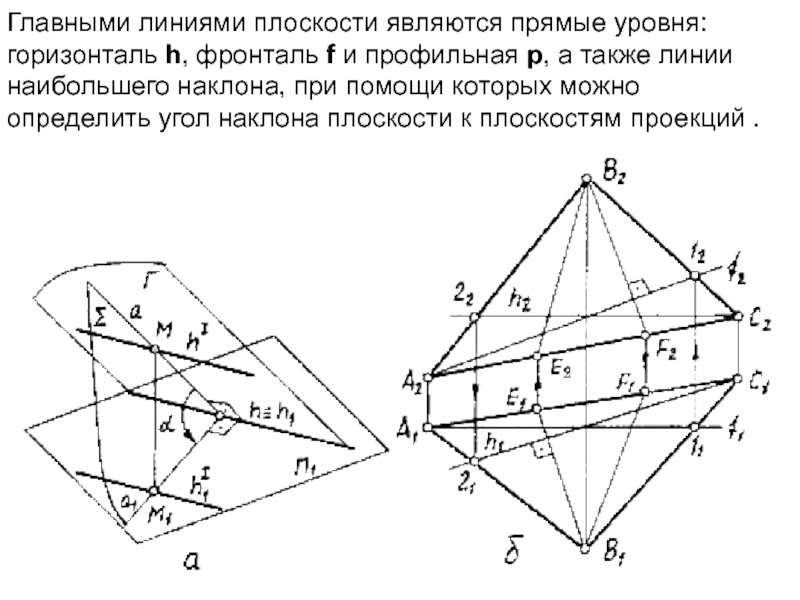
- 12. Главными линиями плоскости являются прямые уровня: горизонталь h,
- 13. Линиями наибольшего наклона называют прямые данной плоскости
- 14. Взаимное положение прямой и плоскости, 2-х плоскостейПлоскости
- 15. Прямая перпендикулярна плоскости, если она перпендикулярна двум
- 16. Плоскости перпендикулярны, если одна плоскость проходит через
- 17. На пересечение прямой с плоскостью составляем алгоритм нахождения их
- 18. Слайд 18
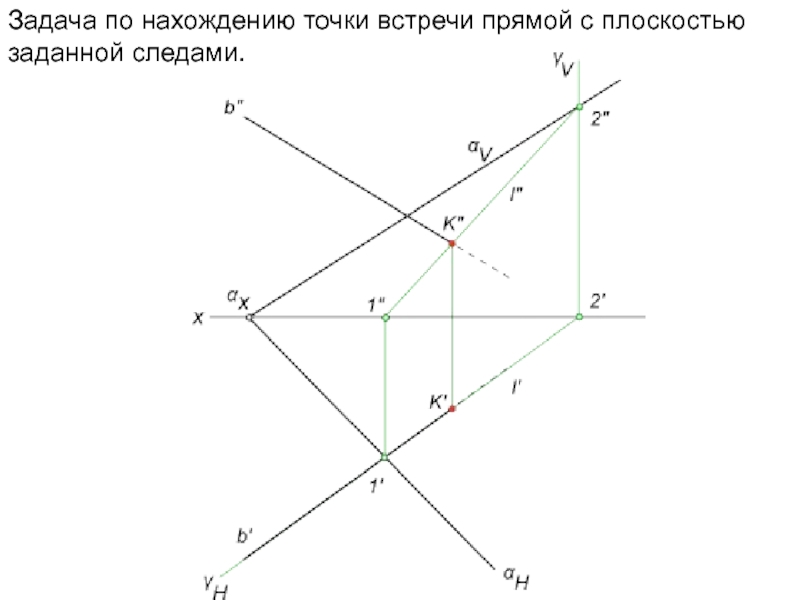
- 19. Задача по нахождению точки встречи прямой с плоскостью заданной следами.
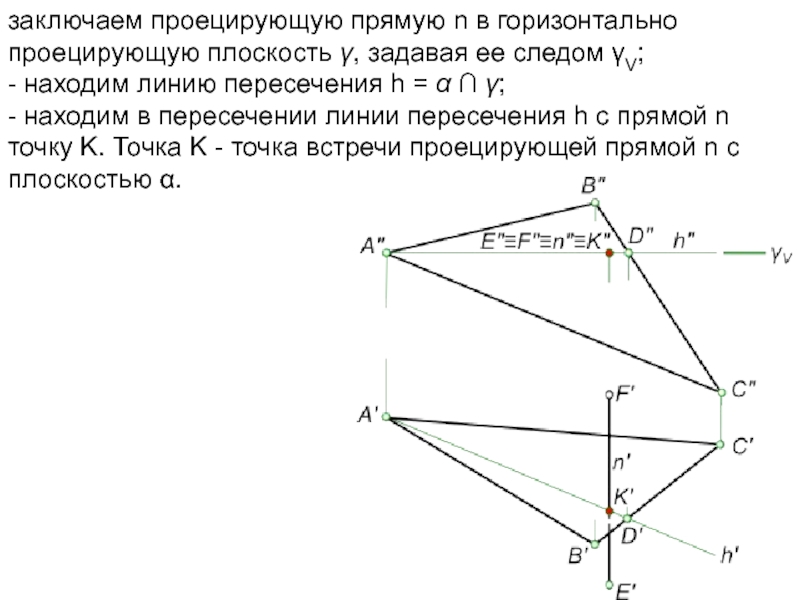
- 20. заключаем проецирующую прямую n в горизонтально проецирующую
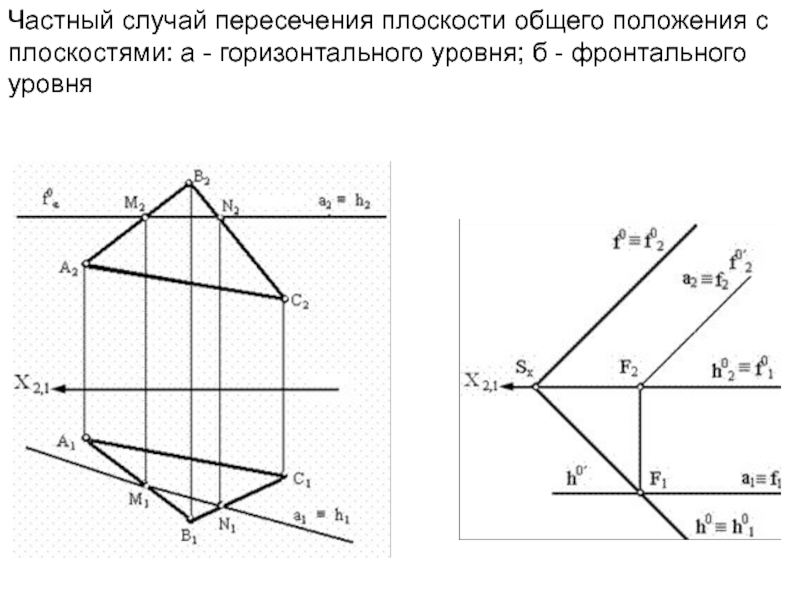
- 21. Частный случай пересечения плоскости общего положения с плоскостями: а - горизонтального уровня; б - фронтального уровня
- 22. Скачать презентанцию
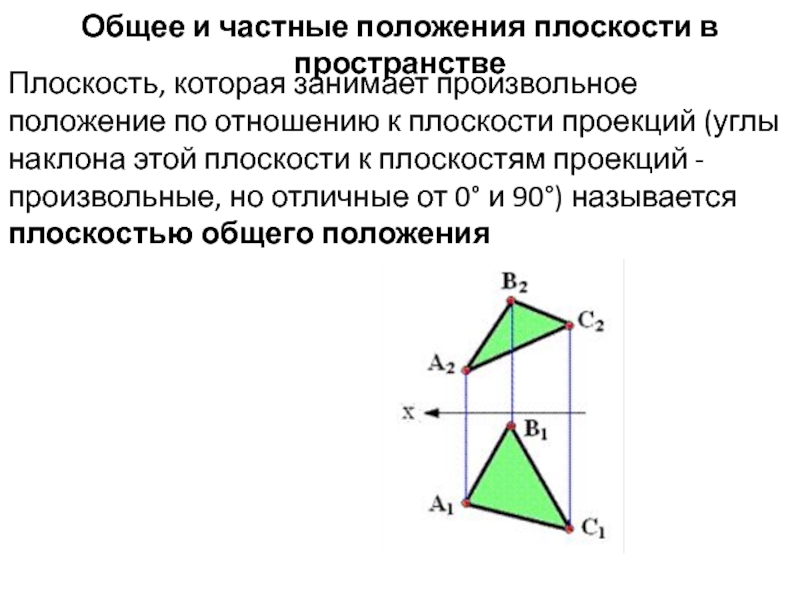
Общее и частные положения плоскости в пространствеПлоскость, которая занимает произвольное положение по отношению к плоскости проекций (углы наклона этой плоскости к плоскостям проекций - произвольные, но отличные от 0° и 90°)
Слайды и текст этой презентации
Слайд 2Общее и частные положения плоскости в пространстве
Плоскость, которая занимает произвольное
положение по отношению к плоскости проекций (углы наклона этой плоскости
к плоскостям проекций - произвольные, но отличные от 0° и 90°) называется плоскостью общего положенияСлайд 3Плоскости, перпендикулярные плоскостям проекций
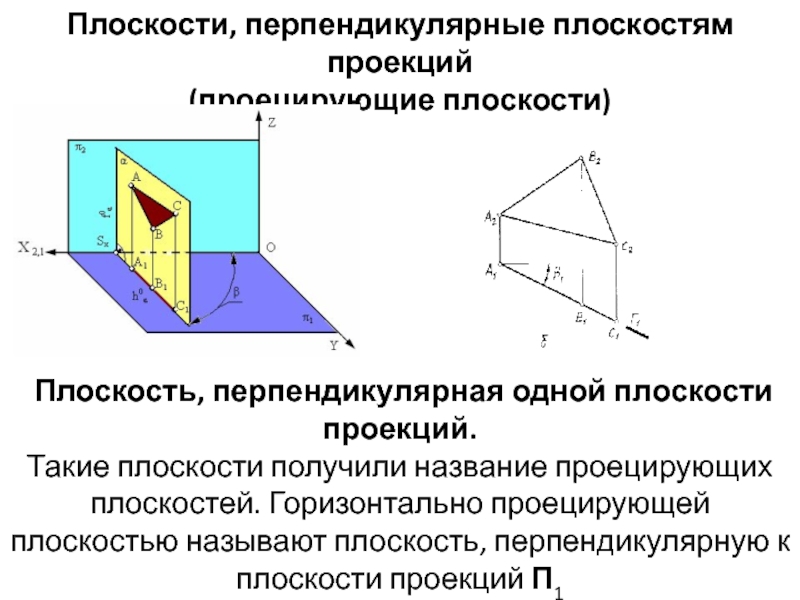
(проецирующие плоскости)
Плоскость, перпендикулярная одной плоскости проекций.
Такие плоскости
получили название проецирующих плоскостей. Горизонтально проецирующей плоскостью называют плоскость, перпендикулярную
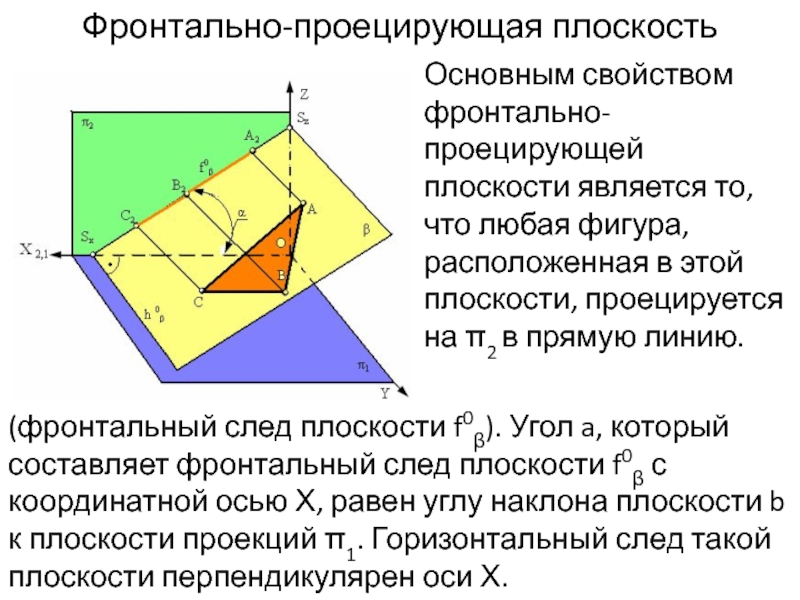
к плоскости проекций П1Слайд 4Основным свойством фронтально-проецирующей плоскости является то, что любая фигура, расположенная
в этой плоскости, проецируется на π2 в прямую линию.
Фронтально-проецирующая плоскость
(фронтальный
след плоскости f0β). Угол a, который составляет фронтальный след плоскости f0β с координатной осью Х, равен углу наклона плоскости b к плоскости проекций π1. Горизонтальный след такой плоскости перпендикулярен оси Х.Слайд 5Профильно-проецирующая плоскость
плоскость, перпендикулярная к профильной плоскости проекций. Любой элемент, лежащий
в этой плоскости, проецируется на профильную плоскость проекций в прямую -
профильный след плоскости. На профильной проекции углы a и b наклона профильно проецирующей плоскости к плоскостям П2 и П1изображаются без искажения.Слайд 6Плоскости, параллельные плоскостям проекций
(плоскости уровня)
Плоскость γ, параллельная плоскости π1, называется
горизонтальной
Любая фигура, расположенная в такой плоскости, проецируется на горизонтальную плоскость
проекций в натуральную величину (Δ А1В1С1 = ΔАВС,). Фронтальный след этой плоскости параллелен оси Х (f0g | | Х).Слайд 7Плоскость, параллельная плоскости π2, называется фронтальной.
Любая линия (прямая или кривая),
принадлежащая плоскости уровня, будет являться линией уровня. Любая фигура, лежащая
в плоскости уровня, проецируется без искажения на плоскость проекций, ей параллельнуюСлайд 9Следом плоскости a называется линия пересечения этой плоскости с плоскостью проекций.
В системе
двух плоскостей проекций π1 и π2 плоскость в общем случае имеет два
следа: горизонтальный ha0 и фронтальный fa0, которые являются пересечением плоскости a соответственно с горизонтальной и фронтальной плоскостями проекцийТочки пересечения плоскости a с координатными осями X, Y, Z называются точками схода следов и обозначаются соответственно Sx, Sy, Sz
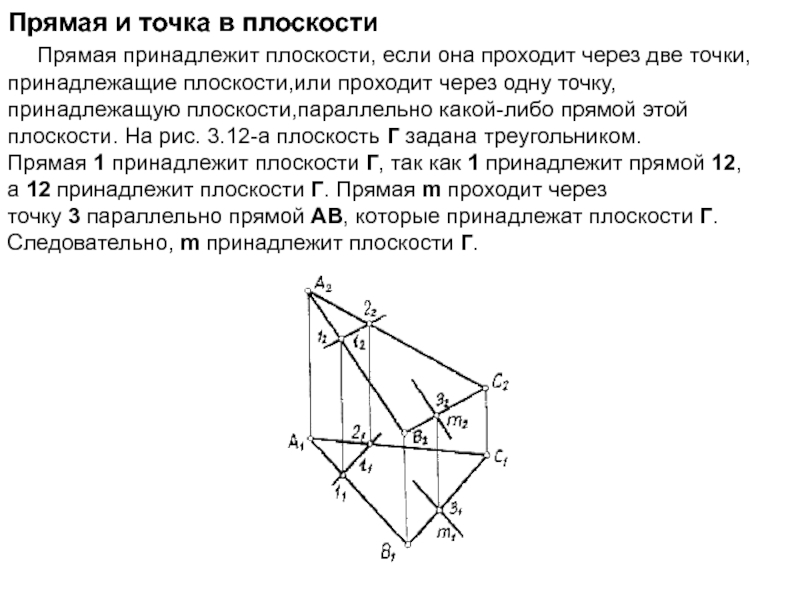
Слайд 10Прямая и точка в плоскости Прямая принадлежит плоскости, если она
проходит через две точки, принадлежащие плоскости,или проходит через одну точку,
принадлежащую плоскости,параллельно какой-либо прямой этой плоскости. На рис. 3.12-а плоскость Г задана треугольником. Прямая 1 принадлежит плоскости Г, так как 1 принадлежит прямой 12, а 12 принадлежит плоскости Г. Прямая m проходит через точку 3 параллельно прямой АВ, которые принадлежат плоскости Г. Следовательно, m принадлежит плоскости Г.Слайд 12Главными линиями плоскости являются прямые уровня: горизонталь h, фронталь f и профильная р, а
также линии наибольшего наклона, при помощи которых можно определить угол
наклона плоскости к плоскостям проекций .Слайд 13Линиями наибольшего наклона называют прямые данной плоскости перпендикулярные к прямым
уровня этой плоскости. Прямая а наибольшего наклона плоскости Г (рис.3.1З-а) к плоскости проекций П1 образует со
своей проекцией а1 на эту плоскость линейный угол двугранного угла плоскостей Г и П1. При этом плоскость Sперпендикулярна прямой h пересечения этих плоскостей и, следовательно, ah и a1 h1. Так как h1 h и h11 h1, то a h1 и a1 h11. Поэтому линия наибольшего наклона данной плоскости к плоскости П1 перпендикулярна к любой горизонтали этой плоскости, и ее горизонтальная проекция перпендикулярна горизонтальной проекции любой горизонтали плоскости. Линию наибольшего наклона к П1 часто называют линией ската.Слайд 14Взаимное положение прямой и плоскости, 2-х плоскостей
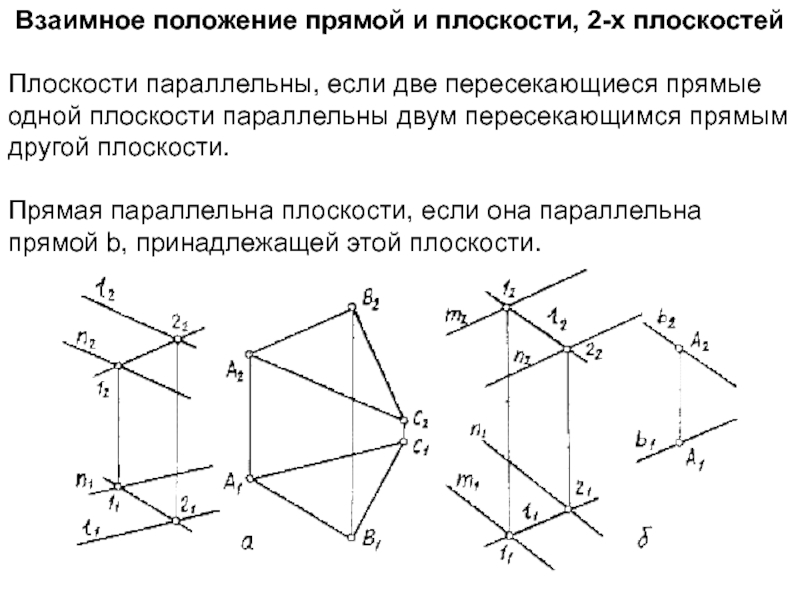
Плоскости параллельны, если две
пересекающиеся прямые одной плоскости параллельны двум пересекающимся прямым другой плоскости.
Прямая
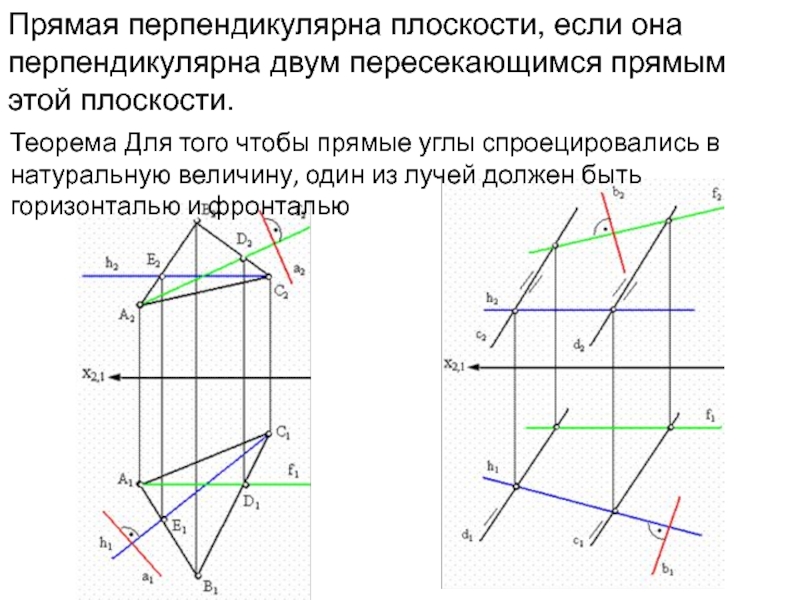
параллельна плоскости, если она параллельна прямой b, принадлежащей этой плоскости.Слайд 15Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой
плоскости.
Теорема Для того чтобы прямые углы спроецировались в натуральную величину,
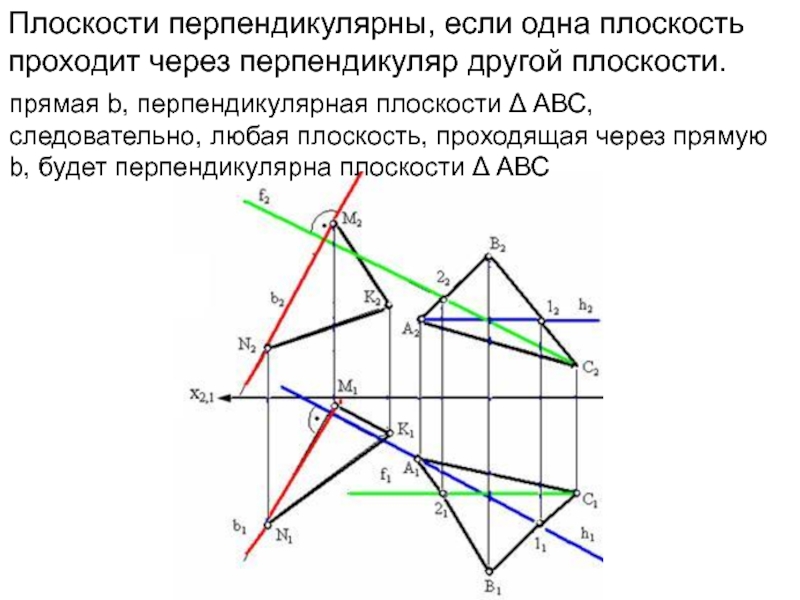
один из лучей должен быть горизонталью и фронтальюСлайд 16Плоскости перпендикулярны, если одна плоскость проходит через перпендикуляр другой плоскости.
прямая
b, перпендикулярная плоскости Δ АВС, следовательно, любая плоскость, проходящая через
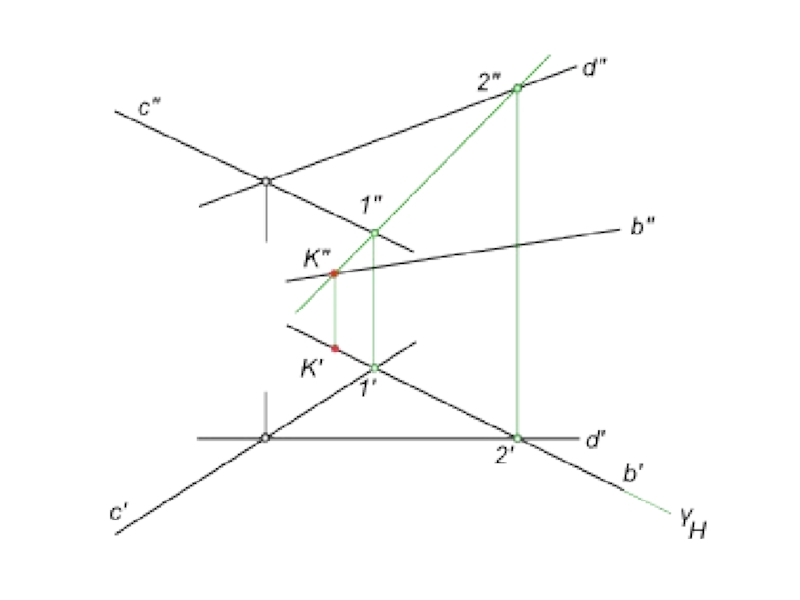
прямую b, будет перпендикулярна плоскости Δ АВССлайд 17На пересечение прямой с плоскостью составляем алгоритм нахождения их точки встречи :
1)
проводим через b` горизонтальный след γH - горизонтально-проецирующей плоскости γ;
2) определяем фронтальную проекцию линии пересечения l,
вспомогательной секущей плоскости γ с данной плоскостью α, используя для этого точки 1` и 2` (принадлежащие данной прямой), в которых горизонтальный след γH пересекает прямые c` и d`;3) определяем точку K"=l"∩b". Зная K", находим K` на пересечении b` с линией связи.