Плоскости и их проекции Определителем плоскости называется совокупность

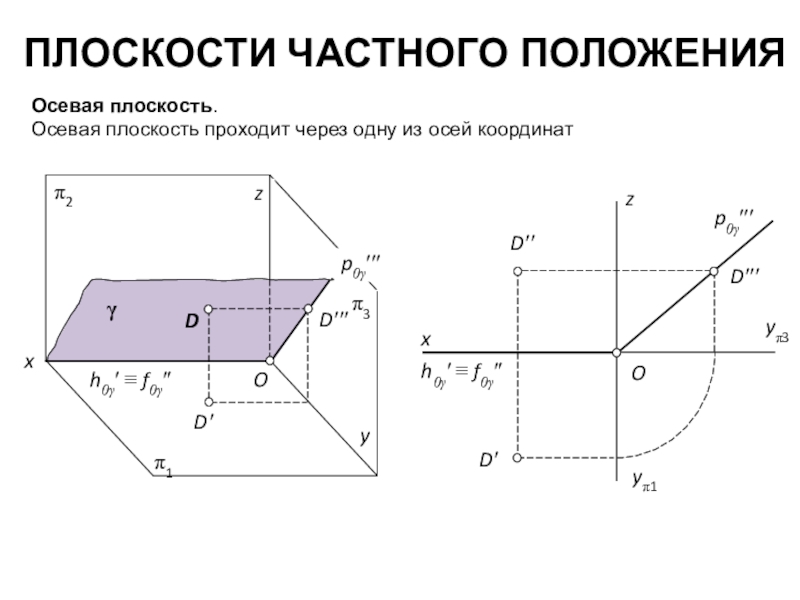
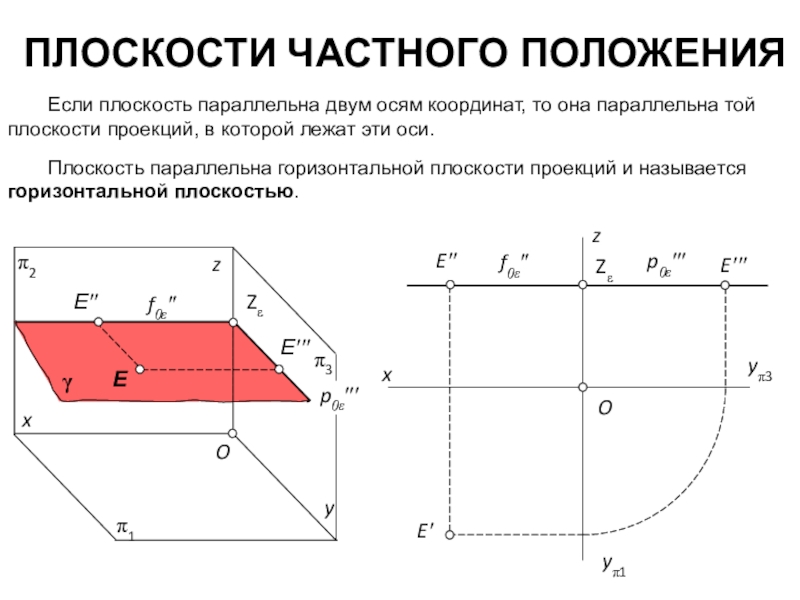
совокупность геометрических элементов, однозначно задающих положение плоскости в пространстве.

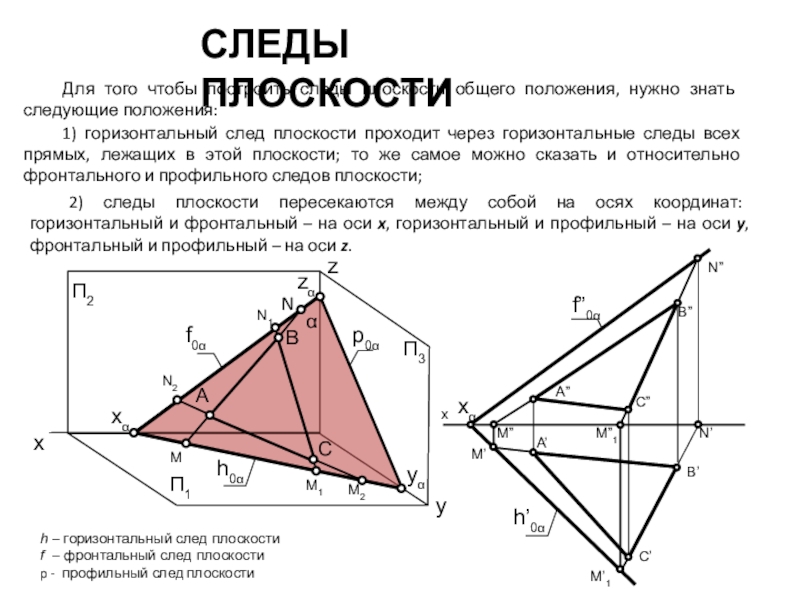
Плоскость считается заданной, если относительно произвольной точки пространства можно однозначно решить вопрос о её принадлежности к этой плоскости.

Плоскость называется плоскостью общего положения, если она не параллельна и не перпендикулярна ни к одной из плоскостей проекций.

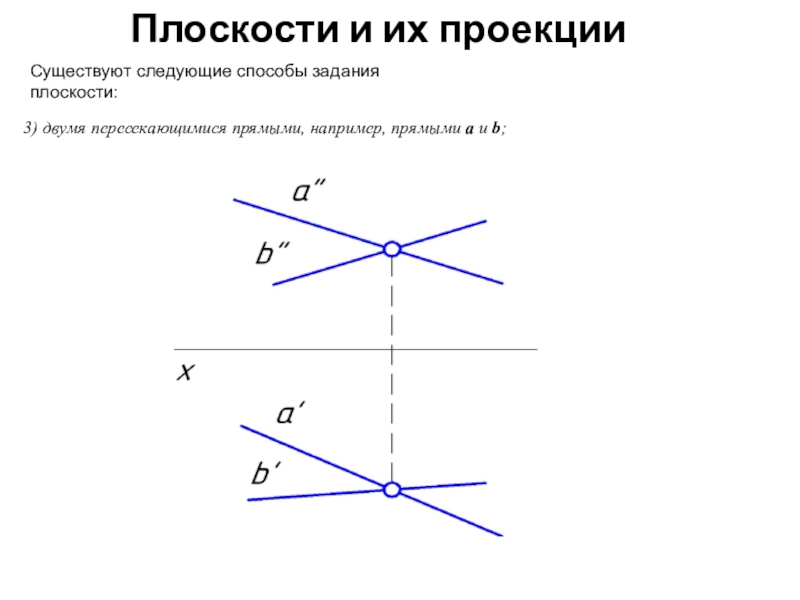
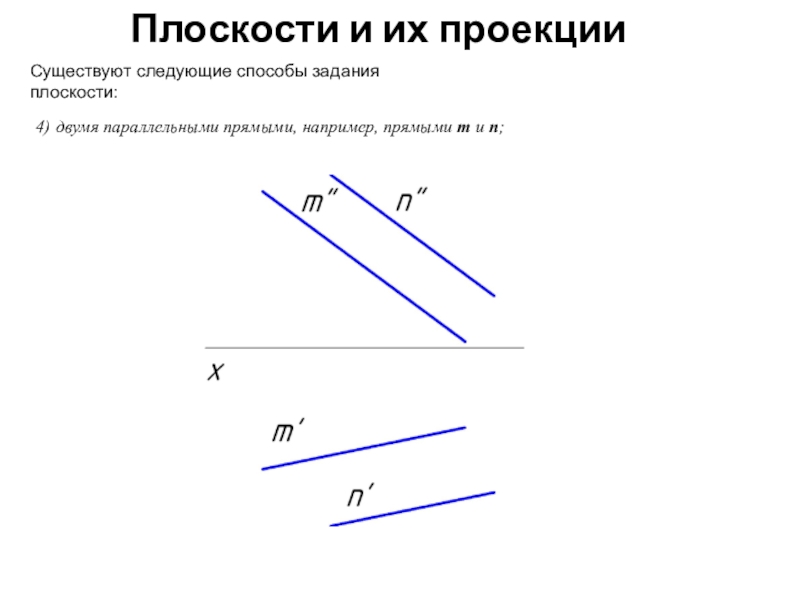
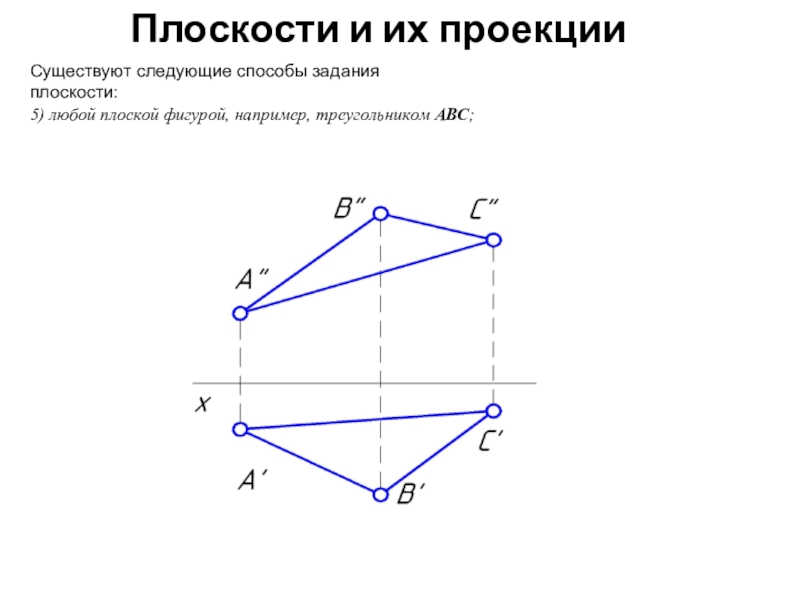
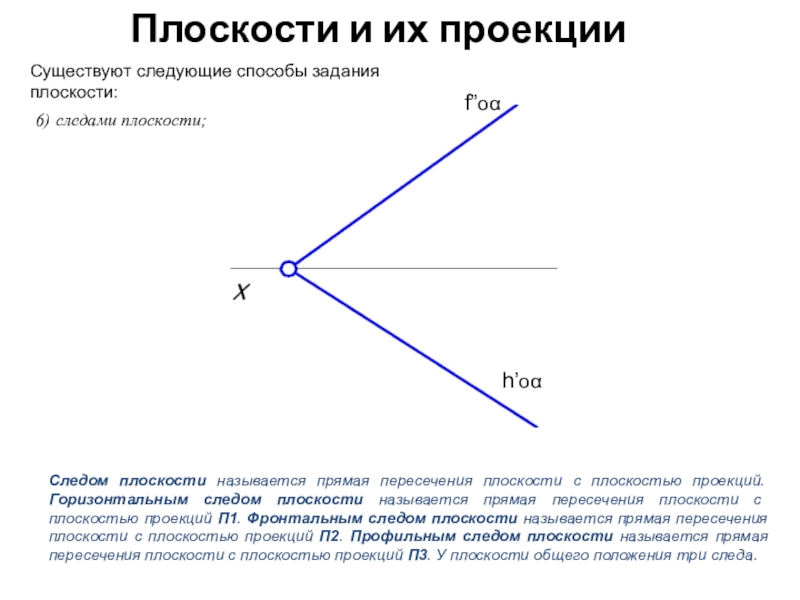
Существуют следующие способы задания плоскости:

1) тремя точками, не лежащими на одной прямой, например, точками А, В и С;

точкой, не лежащей на прямой, например, прямой l и точкой

А;

прямыми, например, прямыми a и b;

прямыми, например, прямыми m и n;

фигурой, например, треугольником АВС;

Следом плоскости называется прямая пересечения плоскости с плоскостью проекций. Горизонтальным

следом плоскости называется прямая пересечения плоскости с плоскостью проекций П1. Фронтальным следом плоскости называется прямая пересечения плоскости с плоскостью проекций П2. Профильным следом плоскости называется прямая пересечения плоскости с плоскостью проекций П3. У плоскости общего положения три следа.

знать следующие положения:
1) горизонтальный след плоскости проходит через горизонтальные следы

всех прямых, лежащих в этой плоскости; то же самое можно сказать и относительно фронтального и профильного следов плоскости;

2) следы плоскости пересекаются между собой на осях координат: горизонтальный и фронтальный – на оси x, горизонтальный и профильный – на оси y, фронтальный и профильный – на оси z.

П2

П1



C

В

А

x

M”

M’

M”1

N’

N”

C”

A”

B”

A’

C’

B’

M’1

M

M1

M2

N1

N

N2

h – горизонтальный след плоскости
f – фронтальный след плоскости
p - профильный след плоскости

x

f0

h0

П3

y

z

y

x

z

p0

h’0

f”0

x

и параллельные плоскостям проекций.
Плоскость перпендикулярная какой–либо плоскости проекций называется проецирующей.
Плоскость

перпендикулярная к плоскости П1 – называется горизонтально проецирующей

фронтально проецирующей

профильно проецирующей

осей координат

она параллельна той плоскости проекций, в которой лежат эти оси.

Плоскость параллельна горизонтальной плоскости проекций и называется горизонтальной плоскостью.

плоскости, т.е. плоскости параллельные соответственно фронтальной и профильной плоскостям проекций.
Такие

плоскости также являются двояко-проецирующими плоскостями, т.е. перпендикулярными к двум другим плоскостям проекций.
Все, что лежит в такой плоскости в двух плоскостях проекций (к которым она перпендикулярна) проецируется на ее следы, а на третью плоскость проекций (которой она параллельна) – в истинную величину.