Полуплоскость и угол

плоскости относительно данной прямой.
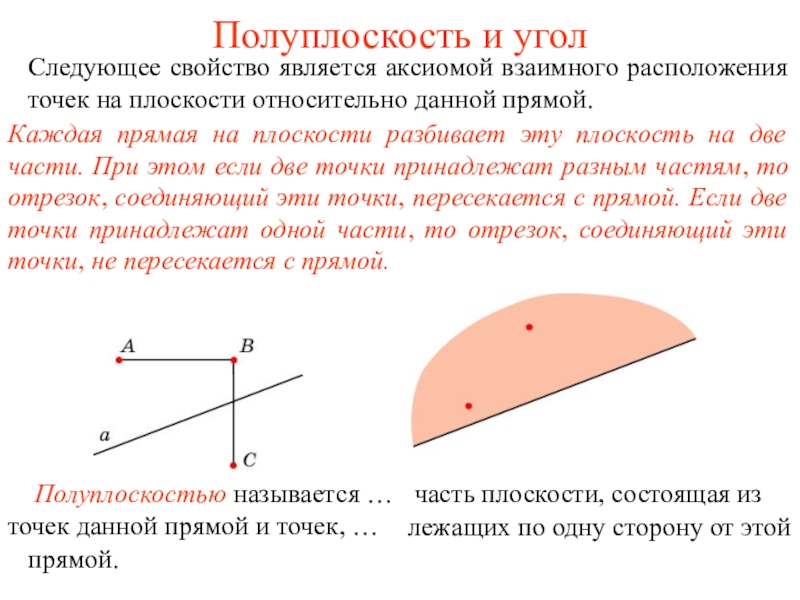
Каждая прямая на плоскости разбивает эту

Полуплоскостью называется …

часть плоскости, состоящая из точек данной прямой и точек, …

лежащих по одну сторону от этой прямой.

одна сторона у них общая, а две другие …

вместе составляют одну прямую.

стороны одного угла дополняют до прямых стороны другого угла.

одной из частей плоскости, ограниченной этими лучами.

Общая вершина называется…

вершиной угла.

Сами лучи называются…

сторонами угла.

двумя лучами с общей вершиной и …

является операция откладывания данного угла в ту или другую сторону

В качестве аксиом принимаются следующие свойства.
От любого луча на плоскости в заданную сторону можно отложить только один угол, равный данному.
Все развернутые углы равны.

прямого, но меньше развернутого угла.

Чтобы сложить два угла, например АОВ и CО1D, отложим угол

пересекается с прямой.
В каком случае две точки принадлежат:
а) одной

б) если отрезок, соединяющий эти точки, не пересекается с прямой.

называется сторонами угла?
Ответ: Фигура, образованная двумя лучами с общей

его стороны вместе составляют прямую.

одна сторона у них общая, а две другие составляют вместе

стороны одного угла дополняют до прямых стороны другого угла.

равными, если один получается из другого операцией откладывания угла.

АОВ и CО1D, отложим угол CO1D от луча ОВ так,

А1O1В1?
Ответ: Если при откладывании угла АOВ от луча O1В1 луч

угла CQD вычесть меньший угол AOB, от луча QC отложим

угол называется: а) прямым; б) острым; в) тупым?
б) угол, меньший

в) угол, больший прямого угла, но меньший развернутого угла, называется тупым.

образованных лучами, на которые делятся данные прямые точкой их пересечения.

Что называется углом между пересекающимися прямыми?

углы.
Какие прямые называются перпендикулярными?

на два равных угла
Что называется биссектрисой угла?

их?
Ответ: AOB, AOC, AOD, BOC, BOD, COD; 6 углов.

рисунке.
Ответ: а) AOB и DOE, BOC и EOF, COD

б) AOB и BOD, BOC и COE, COD и DOF, DOE и EOA, EOF и FOB, FOA и AOC.

одновременно: а) острыми; б) прямыми; в) тупыми?
б) да.
в)

на рисунке.
Ответ: а) AOB, AOC, BOC, BOD, COD, COE,

б) AOD, BOE;

в) AOE, AOF, BOF.

*в) n лучей, каждый из которых имеет начало в вершине

Ответ: а) 6;

б) 15;

В 3 ч и 9 ч.

развернутый угол?
Ответ: 24 раза.