Слайд 1Понятие графа Простейшие свойства графа
11 класс
Слайд 2Теория графов
Теория графов – одна из немногих математических теорий, для
которых точно известен ее создатель, время и место создания: Леонард
Эйлер, 1736 год, г. Петербург.
Именно в этом году Л.Эйлером в «Записках Петербургской академии наук» была опубликована статья, в которой приводилось решение широко теперь известной задачи о Кенигсбергских мостах.
В ней великий математик сформулировал и обосновал критерий, позволяющий отвечать на данный вопрос для любого графа.
Слайд 3Задача о Кенигсбергских мостах
Философ Иммануил Кант, гуляя по городу Кенигсбергу
(сейчас этот город называется Калининград), поставил задачу (1736), известную в
математике как задача о семи кенигсбергских мостах: можно ли пройти по всем этим мостам и при этом вернуться в исходную точку так, чтобы по каждому мосту пройти только один раз.
Слайд 4Что такое граф
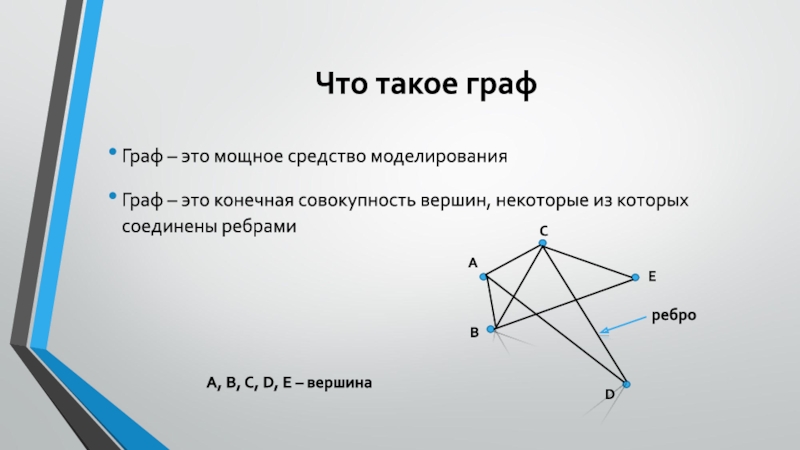
Граф – это мощное средство моделирования
Граф – это
конечная совокупность вершин, некоторые из которых соединены ребрами
A, B, C,
D, E – вершина
А
В
С
D
E
ребро
Слайд 5Мультиграф
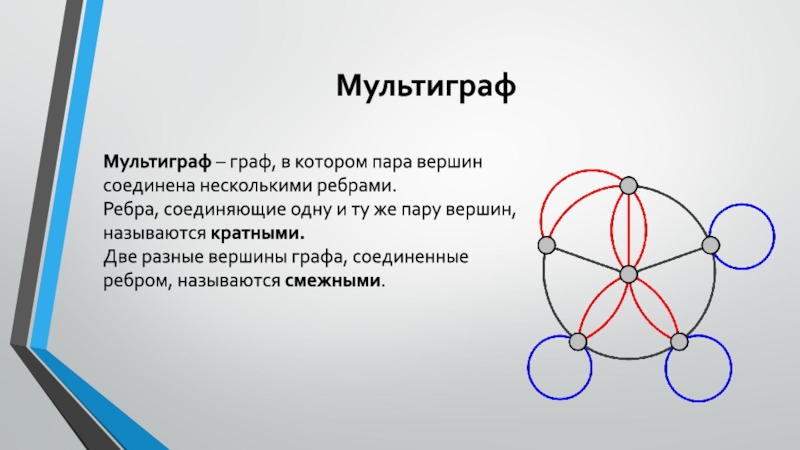
Мультиграф – граф, в котором пара вершин соединена несколькими
ребрами.
Ребра, соединяющие одну и ту же пару вершин, называются кратными.
Две
разные вершины графа, соединенные ребром, называются смежными.
Слайд 6Степень вершин
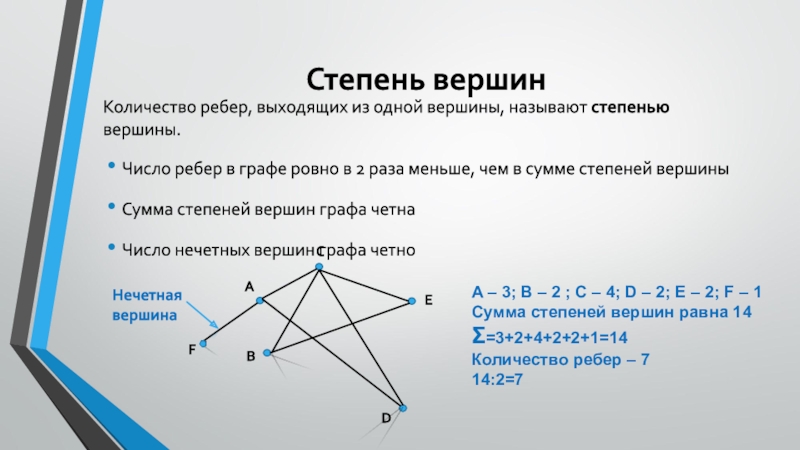
Количество ребер, выходящих из одной вершины, называют степенью вершины.
Число
ребер в графе ровно в 2 раза меньше, чем в
сумме степеней вершины
Сумма степеней вершин графа четна
Число нечетных вершин графа четно
С
А
В
D
E
F
Нечетная вершина
A – 3; B – 2 ; C – 4; D – 2; E – 2; F – 1
Сумма степеней вершин равна 14
=3+2+4+2+2+1=14
Количество ребер – 7
14:2=7
Слайд 7Свойства графа
В любом графе есть, по крайней мере, две вершины,
имеющие одинаковую степень.
Для любого графа количество вершин нечетной степени всегда
будет четное.
Сумма степеней всех вершин графа равна удвоенному числу его ребер.
Слайд 8Маршрут на графике
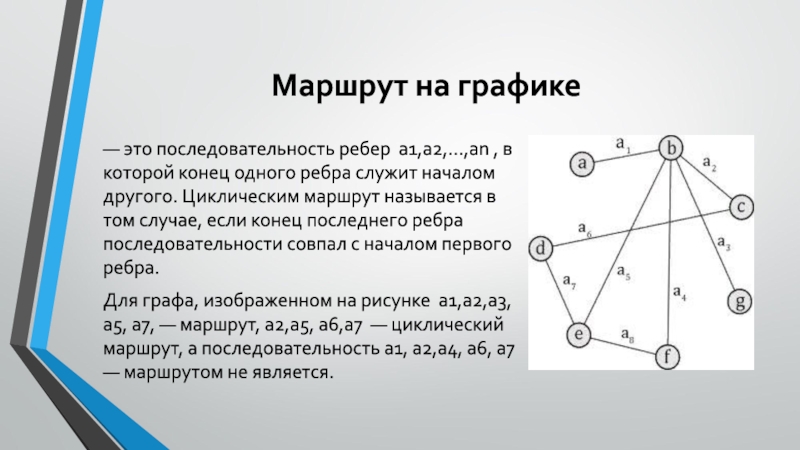
— это последовательность ребер a1,a2,...,an , в
которой конец одного ребра служит началом другого. Циклическим маршрут называется
в том случае, если конец последнего ребра последовательности совпал с началом первого ребра.
Для графа, изображенном на рисунке a1,a2,a3, a5, a7, — маршрут, a2,a5, a6,a7 — циклический маршрут, а последовательность a1, a2,a4, a6, a7 — маршрутом не является.
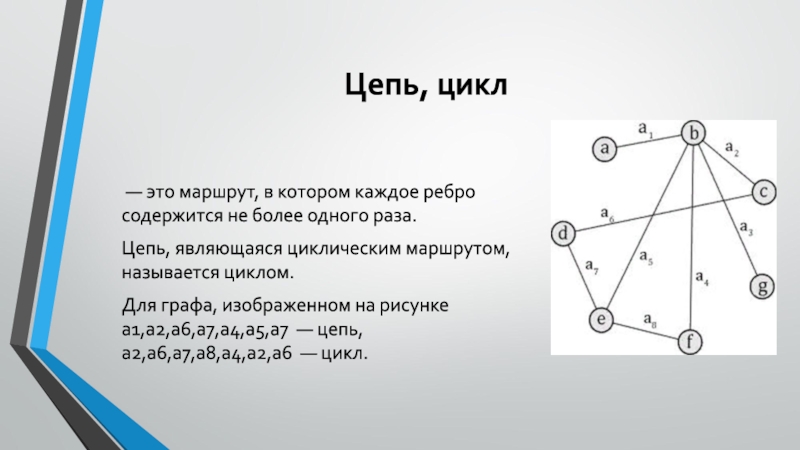
Слайд 9Цепь, цикл
— это маршрут, в котором каждое ребро содержится не
более одного раза.
Цепь, являющаяся циклическим маршрутом, называется циклом.
Для графа, изображенном
на рисунке a1,a2,a6,a7,a4,a5,a7 — цепь, a2,a6,a7,a8,a4,a2,a6 — цикл.
Слайд 10Цепь, цикл
Цепь называется простой, если проходит через каждую свою вершину ровно один раз.
Цикл называется простым, если является простой цепью.
Для графа, изображенном на рисунке, a1,a2,a6,a7,a4
— простая цепь, a2,a6,a7,a8,a4 — простой цикл.
Слайд 11Связный граф
Связанные вершины — это вершины a и b ,
для которых существует цепь, начинающаяся в a и заканчивающаяся в
b .
Связный граф — это граф, у которого любые две вершины связанны. Если граф несвязен, то в нем можно выделить так называемые связанные компоненты (т.е. множества вершин, соединенных ребрами исходного графа, каждое из которых является связным графом).
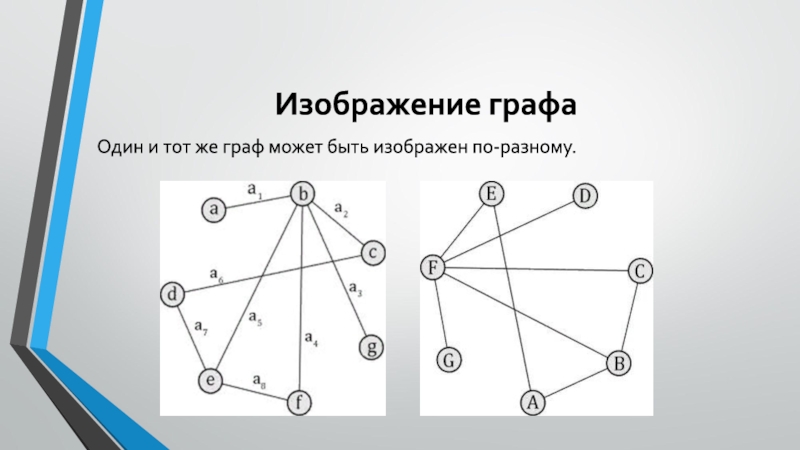
Слайд 12Изображение графа
Один и тот же граф может быть изображен по-разному.
Слайд 13Задачи
(выполнить во время урока)
В графе 30 вершин и 80
ребер, каждая вершина имеет степень 5 или 6. Сколько в
нем вершин степени 5?
В графе каждая вершина имеет степень 3, а число ребер заключено между 16 и 20. Сколько вершин в этом графе?
Слайд 14Домашнее задание
1. Задача
Существует ли граф с пятью вершинами и следующим
набором степеней вершин
а) 0, 1, 2,3,4;
б) 1, 1,
2, 3, 4;
в) 1, 1, 2, 2, 4;
г) 1, 1, 2, 3, 3?
При ответе «Да» надо предъявить соответствующий граф,
ответ «Нет» надо обосновать.
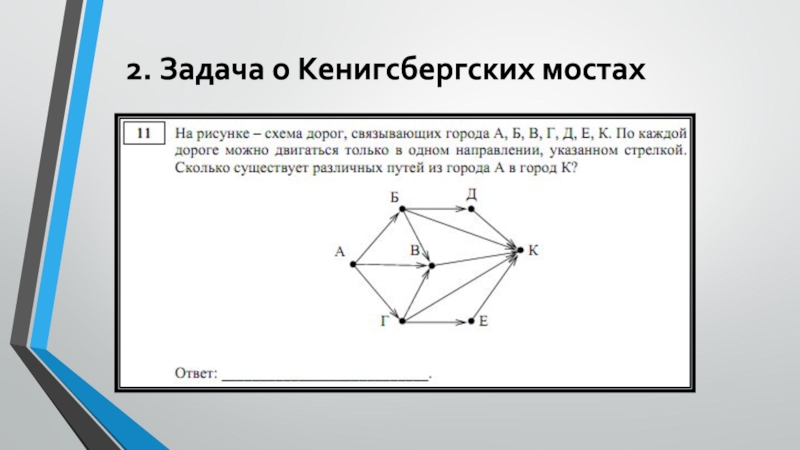
Слайд 152. Задача о Кенигсбергских мостах