Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ. СИНТЕЗ КООМБИНАЦИОННЫХ АВТОМАТОВ
Содержание
- 1. ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ. СИНТЕЗ КООМБИНАЦИОННЫХ АВТОМАТОВ
- 2. ТЕОРИЯ АВТОМАТОВАвтома́т (греч. αυτόματος — самодействующий, самодвижущийся) — устройство, выполняющее определённые функции без помощи человека.
- 3. ЧТО ТАКОЕ АВТОМАТ?АВТОМАТ – в средние века
- 4. Автоматоны Дро Пьер Жаке Дро (1721—1790), известный
- 5. Автоматоны Автоматоны Дро по праву считаются первыми
- 6. АвтоматоныМузыкант — это девушка, играющая на органе и
- 7. ХудожникХудожник — это автоматон, созданный в 1773 году
- 8. КалиграфКалиграф — это самый сложный автоматон, завершенный
- 9. Автома́т-оружиеАвтома́т (от греч. αυτόματος — самодействующий, самодвижущийся — русское
- 10. ТЕОРИЯ АВТОМАТОВТЕОРИЯ АВТОМАТОВ - раздел дискретной математики
- 11. Автоматизация Автоматизация — одно из направлений научно-технического
- 12. Автоматизированные системыТребует дополнительного применения датчиков (сенсоров), устройств
- 13. АвтоматизацияАвтоматизация, за исключением простейших случаев, требует комплексного,
- 14. АСУ и САУСистемы управления разделяют на два
- 15. АСУ
- 16. СИСТЕМЫ АВТОМАТИЗАЦИИ
- 17. Робот-гуманоид ASIMOРобот-гуманоид ASIMO, производство HondaРобот
- 18. Космические аппараты
- 19. Военная техникаРакеты
- 20. Военная техникаТополь-М
- 21. Военная техника
- 22. Данный прототип показывает лишь примерный облик того
- 23. Учёные взялись за дело всерьёз, и затянувшаяся
- 24. Япония готовится принять на работу 3,5 миллиона роботов Роботы
- 25. 1.ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ. Конечным автоматом
- 26. Функция переходовФункция переходов представляет собой отображение ϕ:
- 27. Функция выходовФункция выходов представляет собой отображение ψ:
- 28. Автоматы Мили и МураФункция выходов: z(t)=ψ[x(t),y(t)] –
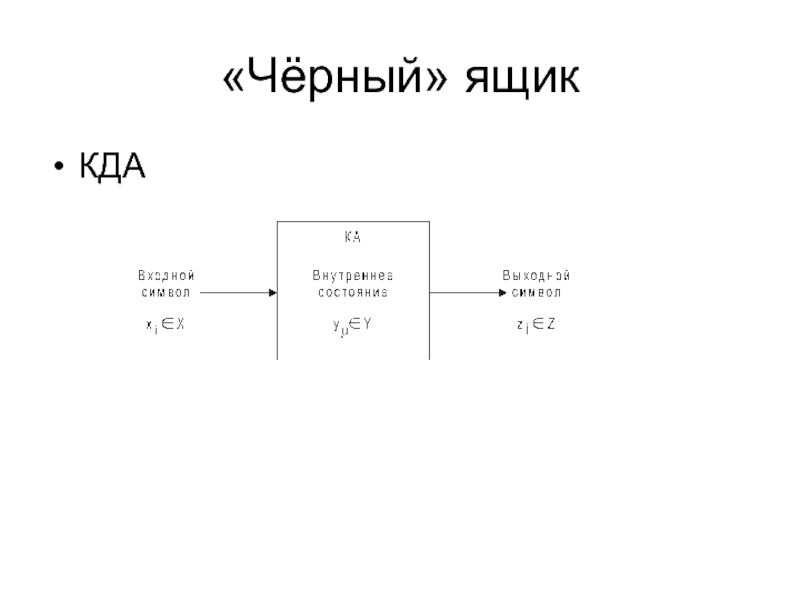
- 29. «Чёрный» ящикКДА
- 30. Таблицы переходов и выходовПоскольку функции ϕ и
- 31. Техническая интерпретация автоматовКонечный автомат представляет собой хотя
- 32. Техническая интерпретация автоматовВходной символ (буква) – это
- 33. Техническая интерпретация автоматовВходное слово – последовательность входных
- 34. 2.Комбинационный автомат Автомат называется комбинационным, если для
- 35. Комбинационный автоматТакой автомат задается тройкой:S=,где X –
- 36. Комбинационный автоматКомбинационный автомат интерпретируется некоторой переключательной схемой или схемой из функциональных элементов:
- 37. 3.Задачи теории конечных автоматовЗадачами теории конечных автоматов
- 38. Синтез автоматовПри синтезе автоматов выделяют следующие этапы:1)
- 39. Синтез автоматов2) структурный синтез – производится минимизация
- 40. Синтез автоматов3) физический синтез – решаются вопросы
- 41. Абстрактный синтезНа этапе абстрактного синтеза осуществляется формализация
- 42. 4. Пример абстрактного синтеза КАВыполнить абстрактный синтез
- 43. Пример абстрактного синтеза КАИз формулировки ясно, что автомат имеет четыре входа и один выход
- 44. Пример абстрактного синтеза КАСтроим соответствующую таблицу истинности
- 45. Пример абстрактного синтеза КАПолучаем символическую форму требуемой ПФ: f(abcd)=0,1,2,4,5,6,8,9,10,12,14 [3,7,11,13,15].Абстрактный синтез завершён.
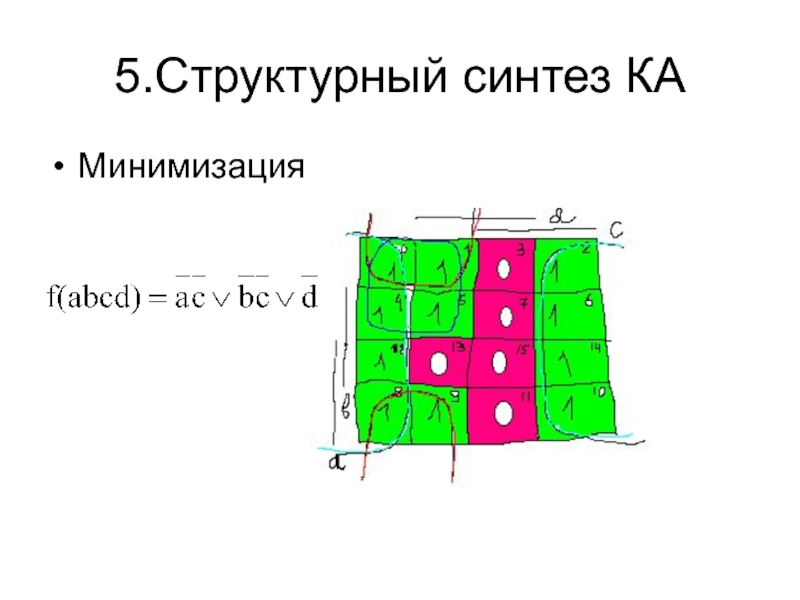
- 46. 5.Структурный синтез КАМинимизация
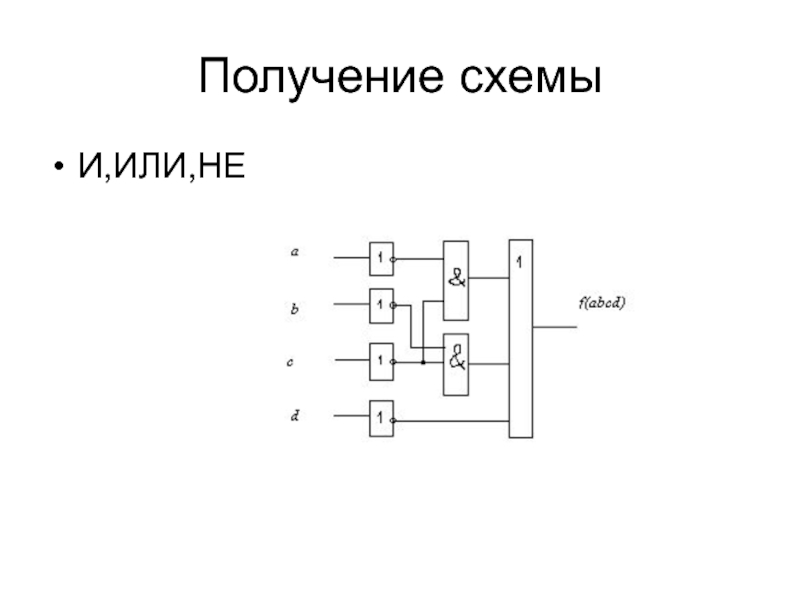
- 47. Получение схемыИ,ИЛИ,НЕ
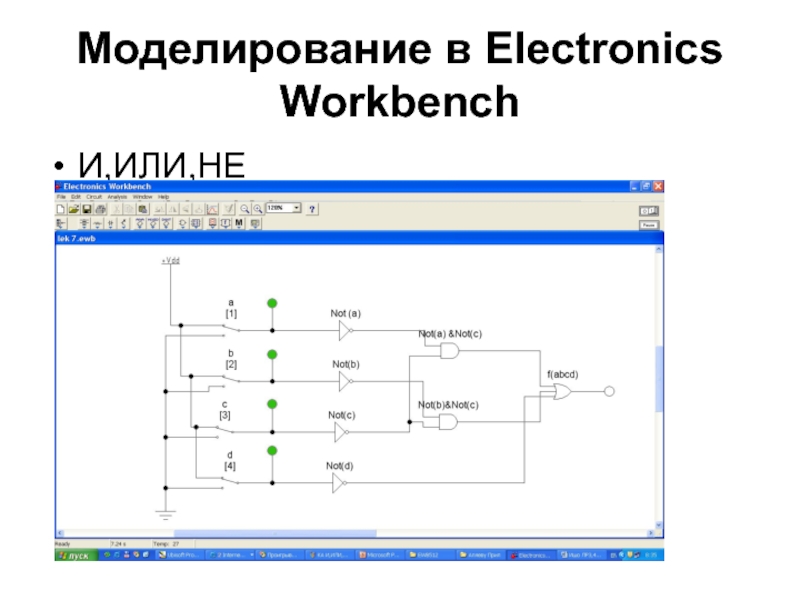
- 48. Моделирование в Electronics WorkbenchИ,ИЛИ,НЕ
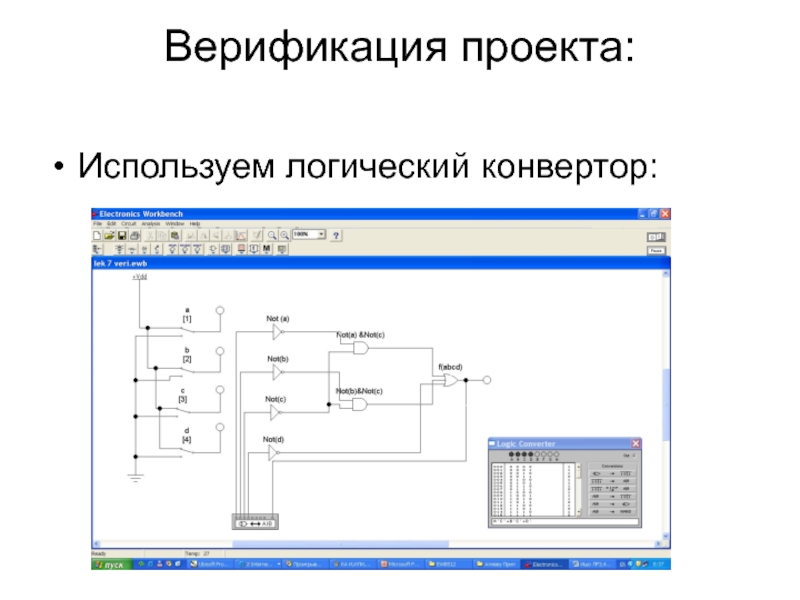
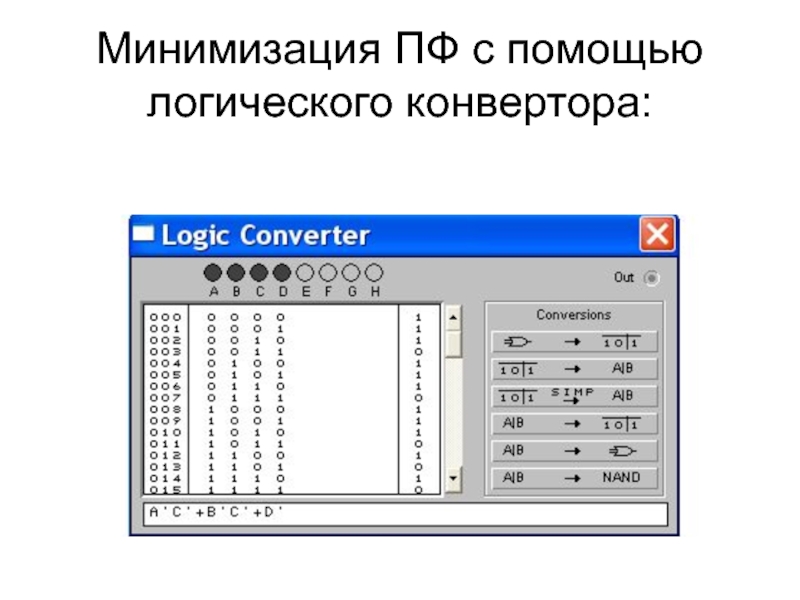
- 49. Верификация проекта: Используем логический конвертор:
- 50. Минимизация ПФ с помощью логического конвертора:
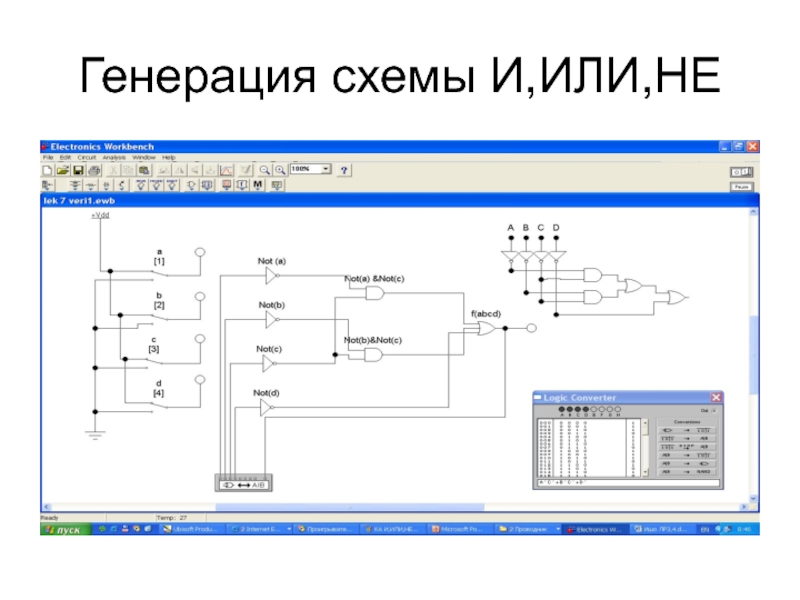
- 51. Генерация схемы И,ИЛИ,НЕ
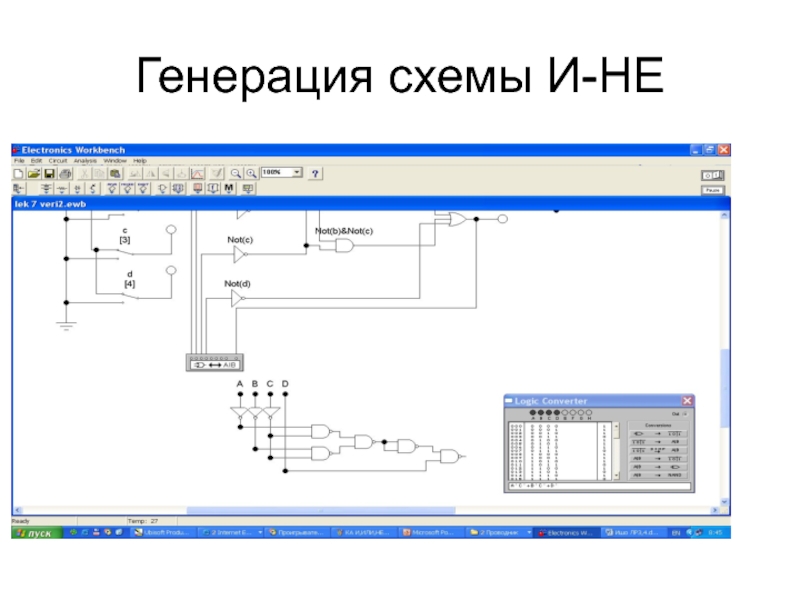
- 52. Генерация схемы И-НЕ
- 53. Скачать презентанцию
ТЕОРИЯ АВТОМАТОВАвтома́т (греч. αυτόματος — самодействующий, самодвижущийся) — устройство, выполняющее определённые функции без помощи человека.
Слайды и текст этой презентации
Слайд 2ТЕОРИЯ АВТОМАТОВ
Автома́т
(греч. αυτόματος — самодействующий, самодвижущийся)
— устройство, выполняющее
определённые функции без помощи человека.
Слайд 3ЧТО ТАКОЕ АВТОМАТ?
АВТОМАТ – в средние века это механизм.
Особенную известность
приобрели в XVIII веке автоматы Вокансона из Гренобля, которые он
показывал в Париже в 1738 г. (человек, игравший на флейте, на свирели, утка, принимавшая пищу), а также произведения мастеров Дро, отца и сына из Лашо-де-Фон в 1790 г.
Слайд 4Автоматоны Дро
Пьер Жаке Дро (1721—1790), известный пионер часового искусства,
родился в 1721 году в городе Ла Шо-де-Фон и положил
начало одной из самых престижных торговых марок.
Слайд 5Автоматоны
Автоматоны Дро по праву считаются первыми компьютерами (?) в
мире, настолько искусно они были выполнены. Где бы их ни
показывали, они всегда производили сенсацию.Сегодня автоматоны можно увидеть в музее Истории и Искусства в Нёвшателе (Швейцария).
Jaquet Droz (Жаке́ Дро) — марка швейцарских часов престижной категории
Слайд 6Автоматоны
Музыкант — это девушка, играющая на органе и состоящая из 2500
деталей. Музыка не поддельная, она не записана и не проигрывается
музыкальной шкатулкой: кукла в самом деле касается пальцами клавиш инструмента, изготовленного по специальному заказу и состоящего из 24 труб. Кукла даже «дышит» (можно увидеть, как двигается грудь), её глаза следят за тем, куда двигаются пальцы, и совершает некоторые движения, как настоящий музыкант.
Слайд 7Художник
Художник — это автоматон, созданный в 1773 году и состоящий из
2000 деталей. Он может рисовать три картинки: портрет Людовика XV
и его собаку с надписью «Mon toutou» (мой пёсик), королевскую чету Марию Антуанетту и Людовика XVI, а так же сцену с Купидоном, управляющим колесницей, запряженной бабочками.Механизм состоит из системы кулачков, которые управляют движением руки в двух измерениях, а так же отвечают за подъем карандаша. Помимо этого, автоматон ёрзает на стуле и периодически сдувает пыль с карандаша.
Слайд 8 Калиграф
Калиграф — это самый сложный автоматон, завершенный в 1772 году
и состоящий из 6000 деталей. Используя механизм, схожий с рисующим
мальчиком, он может писать текст, состоящий из 40 букв. Текст закодирован на колесе и буквы выбираются последовательно друг за другом. Мальчик использует гусиное перо, которое он периодически макает в чернильницу, при этом встряхивает перо, чтобы предотвратить кляксы. Глаза автоматона двигаются вслед за текстом, и голова поворачивается к чернильнице, когда он макает в неё перо.
Слайд 9Автома́т-оружие
Автома́т (от греч. αυτόματος — самодействующий, самодвижущийся — русское название применительно к
оружию) — ручное индивидуальное стрелковое автоматическое оружие, предназначенное для непрерывной или
комбинированной стрельбы. В других странах этот тип оружия называют автоматическим карабином или штурмовой винтовкой (англ. assault rifle).
Слайд 10ТЕОРИЯ АВТОМАТОВ
ТЕОРИЯ АВТОМАТОВ - раздел дискретной математики и математической кибернетики,
изучающий математические модели преобразователей дискретной информации, называемые автоматами.
Такими преобразователями
являются как реальные устройства (вычислительные машины, автоматы, живые организмы и т.д.), так и абстрактные системы (математические машины, аксиоматические теории и т.д.). 
Слайд 11Автоматизация
Автоматизация — одно из направлений научно-технического прогресса, применение технических средств,
методов и систем управления, освобождающих человека от участия в процессах
получения, преобразования, передачи и использования энергии, материалов или информации, существенно уменьшающих степень этого участия или трудоемкость выполняемых операций.
Слайд 12Автоматизированные системы
Требует дополнительного применения датчиков (сенсоров), устройств ввода, управляющих устройств
(контроллеров), исполнительных устройств, устройств вывода, использующих электронную технику и методы
вычислений, иногда копирующие нервные и мыслительные функции человека.Наряду с термином автоматический, используется понятие автоматизированный, подчеркивающий относительно большую степень участия человека в процессе.
Слайд 13Автоматизация
Автоматизация, за исключением простейших случаев, требует комплексного, системного подхода к
решению задачи, поэтому решения стоящих перед автоматизацией задач обычно называются
системами, например:система автоматического управления (САУ);
система автоматизации проектных работ (САПР);
автоматизированная система управления технологическим процессом (АСУ ТП).
Слайд 14АСУ и САУ
Системы управления разделяют на два больших класса:
Автоматизированные Системы
Управления (АСУ) (с участием человека в контуре управления);
Системы Автоматического
Управления (САУ) (без участия человека в контуре управления). 
Слайд 22Данный прототип показывает лишь примерный облик того искусственного сердца, которое
должно быть создано в следующие четыре года техасскими учёными
Слайд 23Учёные взялись за дело всерьёз, и затянувшаяся пьеса "В ожидании
искусственного интеллекта" не означает, что он совсем не придёт.
роботы
Слайд 251.ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ.
Конечным автоматом (просто автоматом) называется система
(пятерка): S=,
в которой Х={х1,х2,...,хi} – конечное входное множество (входной алфавит);
Y={y1,y2,...,yj} – конечное множество внутренних состояний автомата (алфавит состояний); Z={z1,z2,...,zk} – конечное выходное множество (выходной алфавит); ϕ – функция переходов (из состояния в другие состояния); ψ – функция выходов.
Слайд 26Функция переходов
Функция переходов представляет собой отображение ϕ:
или в другом виде:
y(t+1)=ϕ[x(t),y(t)],
где x(t), y(t), y(t+1) –
конкретные символы алфавитов Х и Y соответственно в моменты автоматного времени t, t+1 (в тактах t и t+1); y(t) – называется текущим внутренним состоянием при соответствующем х(t), а y(t+1) – последующим внутренним состоянием.Иначе говоря, функция переходов определяет последующее состояние автомата по заданному текущему и входному символу.
![Функция переходовФункция переходов представляет собой отображение ϕ: или в другом виде:y(t+1)=ϕ[x(t),y(t)],где x(t),](/img/thumbs/2fff79634d86343d53d6b4d86da19df2-800x.jpg "ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ. СИНТЕЗ КООМБИНАЦИОННЫХ АВТОМАТОВ Функция переходовФункция переходов представляет собой отображение ϕ: или в")
Слайд 27Функция выходов
Функция выходов представляет собой отображение ψ: Х×Y→Z или в
другом виде:
z(t)=ψ[x(t),y(t)],
где x(t), y(t), z(t) – конкретные символы алфавитов X,Y,Z
соответственно. Мы не будем особо выделять последующие значения x(t+1) и z(t+1), поэтому зависимость от t будем указывать только для внутреннего состояния, чтобы отделять y(t) от y(t+1).![Функция выходовФункция выходов представляет собой отображение ψ: Х×Y→Z или в другом виде:z(t)=ψ[x(t),y(t)],где x(t), y(t), z(t) – конкретные](/img/thumbs/8b9af975d815a9a3939049f722c9fe47-800x.jpg "ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ. СИНТЕЗ КООМБИНАЦИОННЫХ АВТОМАТОВ Функция выходовФункция выходов представляет собой отображение ψ: Х×Y→Z или в другом")
Слайд 28Автоматы Мили и Мура
Функция выходов: z(t)=ψ[x(t),y(t)] – функция так называемого
автомата Мили.
В теории конечных автоматов рассматривается также автомат Мура, у
которого функция выходов проще – ψ: или z(t)=ψ[y(t)].![Автоматы Мили и МураФункция выходов: z(t)=ψ[x(t),y(t)] – функция так называемого автомата Мили.В теории конечных автоматов рассматривается также](/img/thumbs/08abe4da8d8651a4a499859b60d96ca6-800x.jpg "ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ. СИНТЕЗ КООМБИНАЦИОННЫХ АВТОМАТОВ Автоматы Мили и МураФункция выходов: z(t)=ψ[x(t),y(t)] – функция так называемого автомата")
Слайд 30Таблицы переходов и выходов
Поскольку функции ϕ и ψ определены на
конечных множествах, их можно задавать таблицами. Обычно две таблицы сводят
в одну таблицу ϕ×ψ: и называют таблицей переходов-выходов или просто таблицей переходов (автоматной таблицей).
Слайд 31Техническая интерпретация автоматов
Конечный автомат представляет собой хотя и абстрактную, но
с функциональной точки зрения довольно точную модель дискретного (цифрового) вычислительного
или управляющего (контролирующего) устройства с конечным числом состояний.
Слайд 32Техническая интерпретация автоматов
Входной символ (буква) – это входной сигнал, точнее
комбинация (набор) сигналов на всех входах x1,x2,...,xn (это не буквы
алфавита Х) устройства. Эта комбинация сигналов на дискретных входах еще называется входным вектором (набором) . Выходной сигнал (буква) – комбинация (набор) сигналов на дискретных выходах z1,z2,...,zm (это не буквы алфавита Z) – выходной вектор (набор) .
Слайд 33Техническая интерпретация автоматов
Входное слово – последовательность входных векторов, поступающих в
дискретные моменты времени (такты) t=1,2,3...
Состоянию автомата соответствует вектор – текущее,
– последующее. Этот вектор задает комбинация (набор) состояний y1,y2,...,ys (это не буквы алфавита Y) элементов памяти автомата.Выходное слово – последовательность выходных векторов в дискретные моменты времени.
Слайд 342.Комбинационный автомат
Автомат называется комбинационным, если для любого входного символа
х и любых состояний yi, yj значения функций ϕ переходов
одинаковы: ϕ(х,yi)=ϕ(х,yj)=z, где z – выходной символ. Иначе говоря, выходной символ z не зависит от состояния и определяется текущим входным символом. Говорят, что у такого частного класса автомата все состояния эквивалентны и, следовательно, комбинационный автомат имеет одно состояние.
Слайд 35Комбинационный автомат
Такой автомат задается тройкой:
S=,
где X – множество входных символов,
Z – множество выходных символов, ψ – функция выхода.
Комбинационные автоматы
являются преобразователями информации без памяти и описываются переключательными функциями выходов.
Слайд 36Комбинационный автомат
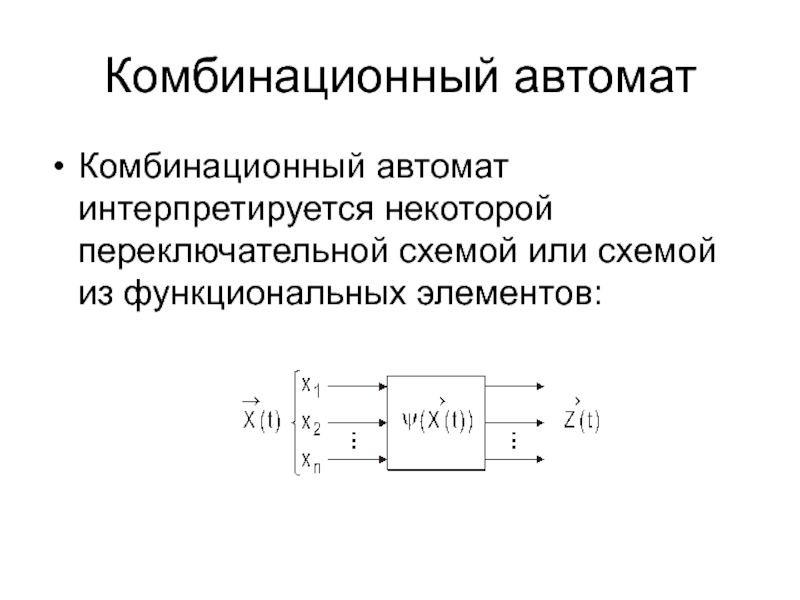
Комбинационный автомат интерпретируется некоторой переключательной схемой или схемой из
функциональных элементов:
Слайд 373.Задачи теории конечных автоматов
Задачами теории конечных автоматов являются:
1) изучение возможностей
автоматов в терминах множеств слов, с которыми они работают (распознавание
входных последовательностей – слов), формирование требуемых выходных, т.е. автоматных отображений;2) распознавание различных свойств автоматов;
3) описание автоматов (анализ) и их реализация, т.е. представление автомата как структуры, состоящей из объектов фиксированной сложности (синтез).
Слайд 38Синтез автоматов
При синтезе автоматов выделяют следующие этапы:
1) абстрактный синтез, или
формализация условий работы, когда от некоторого высокоуровневого описания автомата (например,
на естественном языке – в виде словесной формулировки) переходят к математической модели. Такой моделью может быть таблица истинности для комбинационного автомата, таблица переходов-выходов для последовательностного автомата. В свою очередь по этим моделям получают переключательные функции в символической форме;
Слайд 39Синтез автоматов
2) структурный синтез – производится минимизация переключательных функций, описывающих
автомат, выполняется их представление в виде, соответствующем заданному базису реализации.
Эти
два этапа называют логическим проектированием. Их результатом является функциональная схема автомата (например, функциональная электрическая схема);
Слайд 40Синтез автоматов
3) физический синтез – решаются вопросы построения принципиальной схемы
(например, принципиальной электрической схемы), создания топологии кристалла микросхемы, обеспечения надежности,
помехоустойчивости и в дальнейшем изготовления автомата.
Слайд 41Абстрактный синтез
На этапе абстрактного синтеза осуществляется формализация условий работы, когда
от некоторого высокоуровневого описания автомата (например, на естественном языке –
в виде словесной формулировки) переходят к математической модели. Такой моделью может быть таблица истинности комбинационного автомата. В свою очередь по этим моделям получают переключательные функции в символической форме.
Слайд 424. Пример абстрактного синтеза КА
Выполнить абстрактный синтез автомата по следующей
словесной формулировке:
«Автомат имеет входы abcd и выход z, который
активируется (включается): 1) при отсутствии или неодновременном поступлении сигналов на каналы a и b – тогда, когда отсутствуют или поступают не одновременно сигналы на каналы c и d;
2) при одновременном поступлении сигналов на каналы a и b – тогда, когда не поступает сигнал на канал d.
В остальных случаях выход z не активируется (не включается)».
Слайд 43Пример абстрактного синтеза КА
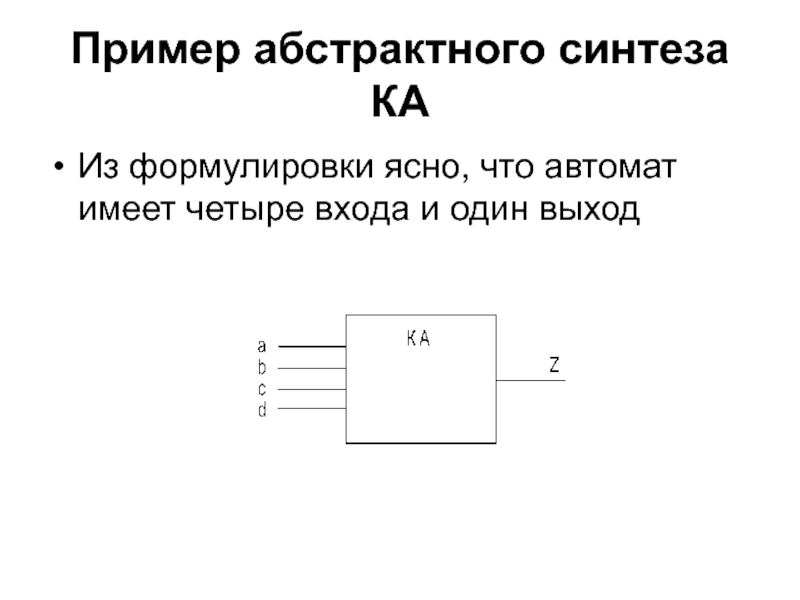
Из формулировки ясно, что автомат имеет четыре
входа и один выход
Слайд 44Пример абстрактного синтеза КА
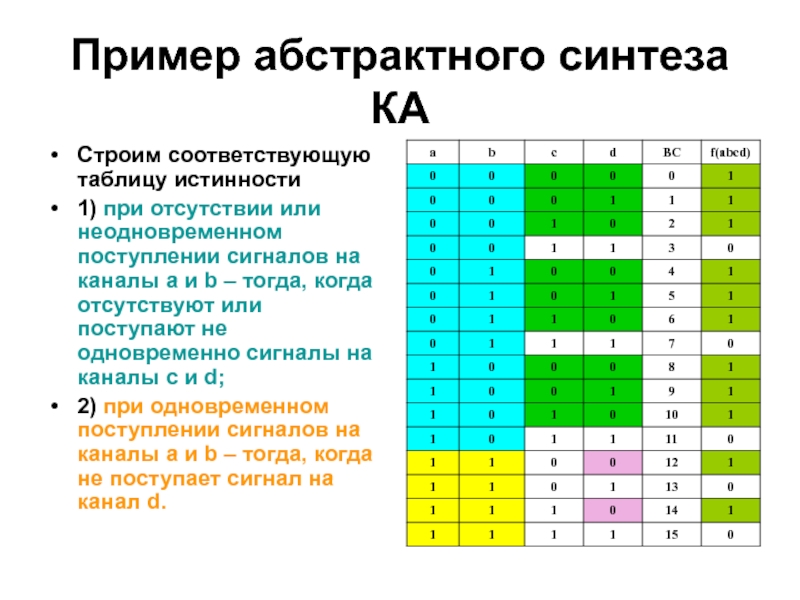
Строим соответствующую таблицу истинности
1) при отсутствии
или неодновременном поступлении сигналов на каналы a и b –
тогда, когда отсутствуют или поступают не одновременно сигналы на каналы c и d;2) при одновременном поступлении сигналов на каналы a и b – тогда, когда не поступает сигнал на канал d.
Слайд 45Пример абстрактного синтеза КА
Получаем символическую форму требуемой ПФ:
f(abcd)=0,1,2,4,5,6,8,9,10,12,14 [3,7,11,13,15].
Абстрактный
синтез завершён.
![Пример абстрактного синтеза КАПолучаем символическую форму требуемой ПФ: f(abcd)=0,1,2,4,5,6,8,9,10,12,14 [3,7,11,13,15].Абстрактный синтез завершён.](/img/thumbs/33305c3e8ccb93f50e63c1e046fb5cfb-800x.jpg "ПОНЯТИЕ О КОНЕЧНОМ АВТОМАТЕ. СИНТЕЗ КООМБИНАЦИОННЫХ АВТОМАТОВ Пример абстрактного синтеза КАПолучаем символическую форму требуемой ПФ: f(abcd)=0,1,2,4,5,6,8,9,10,12,14 [3,7,11,13,15].Абстрактный синтез завершён.")
