Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Понятие ОБРАТНой ФУНКЦИИ
Содержание
- 1. Понятие ОБРАТНой ФУНКЦИИ
- 2. ЗАДАЧИ УРОКАДать определение обратной функцииНаучиться находить область
- 3. Повторение:Известно, что зависимость пути от времени движения
- 4. Задание:Из уравнения 2х – у – 1
- 5. Понятие обратной функцииИз уравнения 2х – у
- 6. Рассмотрим функцию у = х2. При
- 7. Зависимость
- 8. Рассмотрим функцию у = х2 на промежутке
- 9. Вывод 1. Если функция y = f(x)
- 10. Задание на домп. 3.1, 3.2 и конспект
- 11. Подведение итогов урока1. Какую функцию мы сегодня
- 12. Скачать презентанцию
ЗАДАЧИ УРОКАДать определение обратной функцииНаучиться находить область определения и область значений функции, обратной даннойПрименять алгоритм нахождения формулы функции, обратной даннойРассмотреть особенности графиков обратных функций
Слайды и текст этой презентации
Слайд 2ЗАДАЧИ УРОКА
Дать определение обратной функции
Научиться находить область определения и область
значений функции, обратной данной
особенности графиков обратных функцийСлайд 3Повторение:
Известно, что зависимость пути от времени движения тела при его
равномерном движении с постоянной скоростью v выражается формулой
s = vt. Из этой формулы можно найти обратную зависимость – времени от пройденного пути.Получим
Функцию называют обратной к
функции s(t) = vt.
Слайд 4Задание:
Из уравнения 2х – у – 1 = 0 выразите
у через х
у = 2х – 1.
Из
уравнения 2х – у – 1 = 0 выразите х через уИмеем: или
Слайд 5Понятие обратной функции
Из уравнения 2х – у – 1 =
0 мы получили две зависимости:
1) у = 2х – 1,
где у – зависимая переменная,х- независимая переменная, аргумент.
2) , где х – зависимая переменная,
у – аргумент
Слайд 6Рассмотрим функцию у = х2. При у > 0
имеем
и Функция, которая принимает каждое своё значение в единственной точке области определения, называется оборотной.
В приведённых примерах функция у = 2х – 1 является оборотной, а функция у = х2, рассмотренная на всей области определения, не является оборотной.
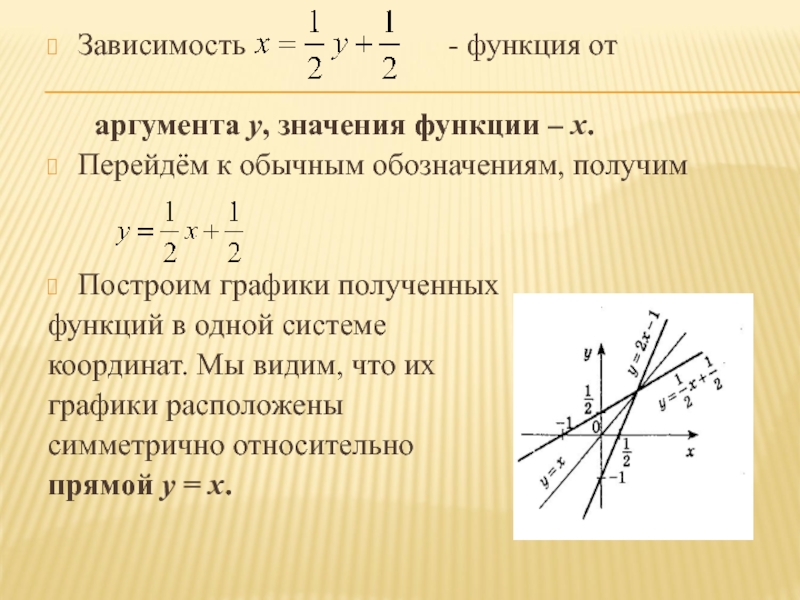
Слайд 7Зависимость
- функция от
аргумента
у, значения функции – х.Перейдём к обычным обозначениям, получим
Построим графики полученных
функций в одной системе
координат. Мы видим, что их
графики расположены
симметрично относительно
прямой у = х.
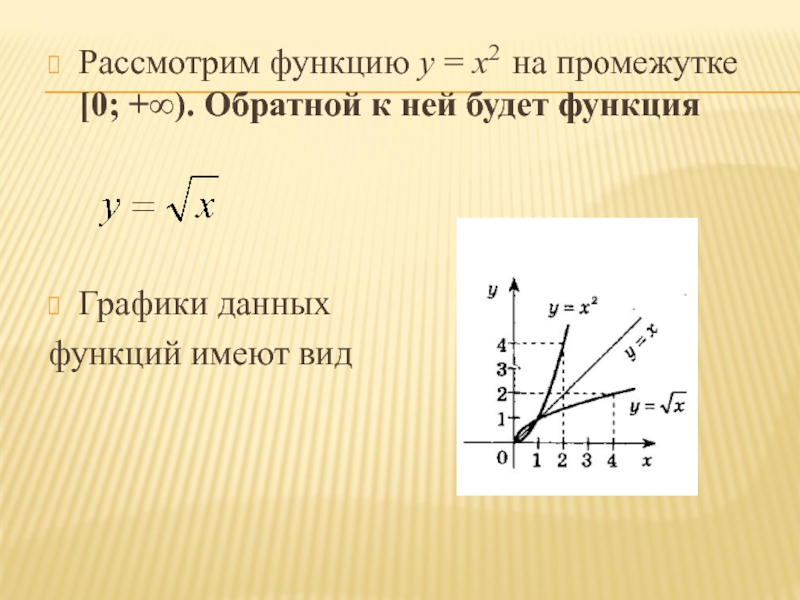
Слайд 8Рассмотрим функцию у = х2 на промежутке [0; +∞). Обратной
к ней будет функция
Графики данных
функций имеют вид
Слайд 9Вывод
1. Если функция y = f(x) задана формулой, то
для нахождения обратной к ней функции нужно решить уравнение f(x)
= y относительно х, а потом поменять местами х и y.2. Если уравнение f(x) = y имеет больше одного корня, то функции, обратной к функции y = f(x), не существует.
3. Графики данной и обратной функции симметричны относительно прямой у = х.
4. Если функция y = f(x) возрастает или убывает на некотором промежутке, то она имеет обратную функцию на этом промежутке, которая возрастает, если f(x) возрастает, и убывает, если f(x) убывает.
Функция, обратная данной, определена на множестве значений функции y = f(x).
Если f и g – функции, обратные одна к другой, то
E (f) = D (g) и D (f) = E (g)
Слайд 10Задание на дом
п. 3.1, 3.2 и конспект – выучить
№ 3.3
(а, в, д, ж), 3.4 (а, в, д); 3.7(б,в).
Повторить свойства
и графики тригонометрических функцийСлайд 11Подведение итогов урока
1. Какую функцию мы сегодня выучили?
2. При каком
условии для заданной функции y = f(x) существует обратная?
3. Как
расположены графики прямой и обратной к ней функций, построенные в одной системе координат?4. Чем является область определения функции y = f(x) для обратной к ней функции?