ПОСТРОЕНИЕ КРИВЫХ В EXCEL

на плоскости пару чисел .
Основными понятиями этой системы являются

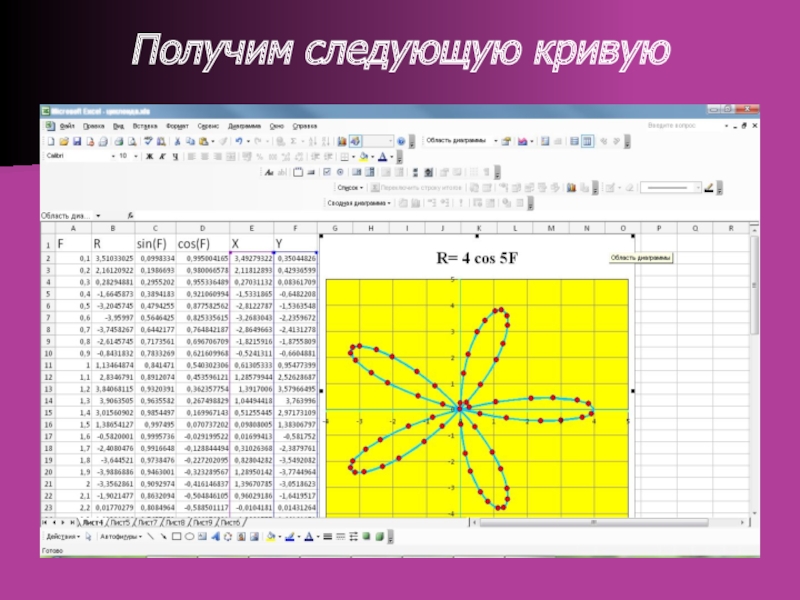
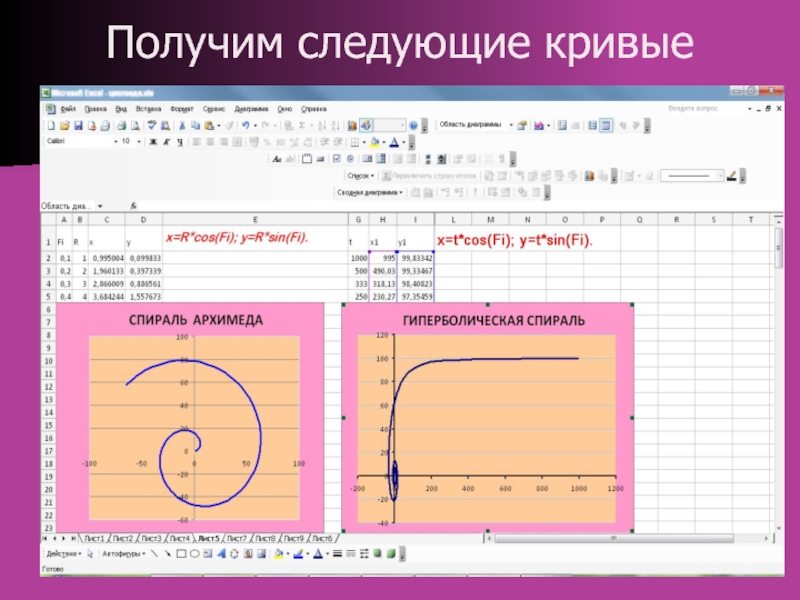
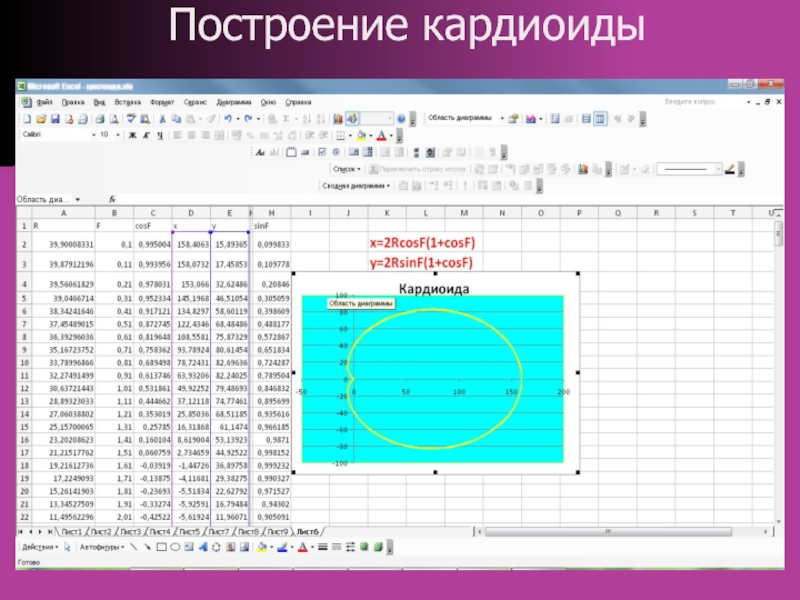
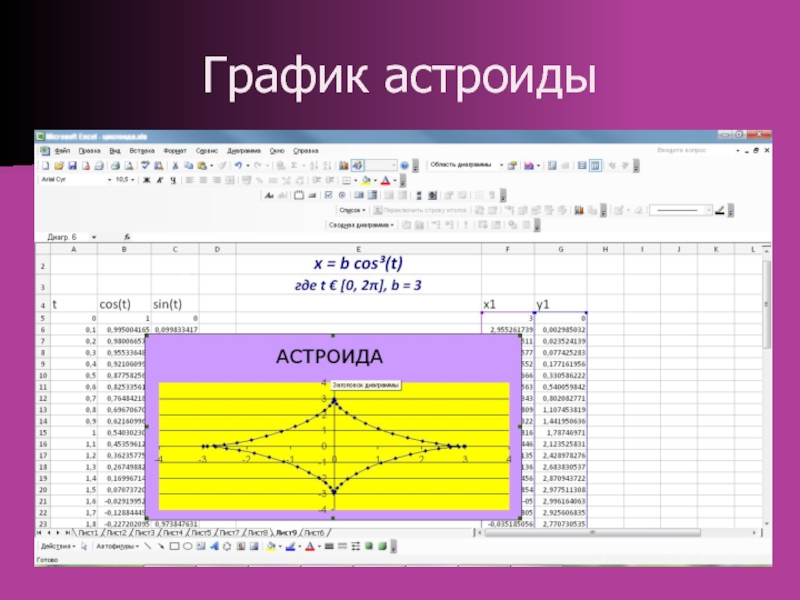
точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось.
Фигуры в полярных координатах
образуются как след конца
бегающего по кругу полярного
радиуса переменной длины.

Длина радиуса определяется
величиной угла, который он
образует с полярной осью.

Знак «+», если угол против
часовой стрелки, и знак «-»
если угол по часовой стрелки.

в полярной. Тогда очевидно, что:

Формулы обратного перехода:
Замечание:
число в полярной системе
определено не однозначно:
парам чисел соответствует
одна и та же точка при любых
натуральных n.

Переход от ДСК к ПСК

из декартовых координат в полярные, используя формулы: X=R*COS(F), Y=R*SIN(F).
Задача.
Построить

кривую, заданную уравнением
Решение. Найдем уравнение линии в полярных координатах
Для программы Microsoft Excel:
R=4*COS(3*F)
Пусть угол
Выберем шаг изменения 0,1
Построим компьютерную модель исследования

=0,1

А3 =А2+0,1
B2 =4*COS(3*F)
C2 =SIN(А2)
D2 =COS(А2)
E2 =B2*D2
F2 =В2*C2

Для построения графика выделим
информационный блок E2..F63, так как аргумент
F, будем изменять от 0,1 до 6,3 радиана. Возможно изменение и до 9,42, 12,56, и т. д.

в двух равномерных движениях, одно из которых совершается вдоль прямой,

а другое – по окружности.



Гиперболическая спираль
По мере роста спираль устремляется к полюсу, делая вокруг него бесконечное множество витков, расстояние между которыми убывает.

(z ̸ 9)² =1 на интервале х,y ∊ [-7;7] с

шагом 0.5 ;
ІІ Вариант. x² ̸ 9 + y² ̸ 4 =2z на интервале х,y ∊ [-5;5] с шагом 0.5 ;
ІІІ Вариант. x² ̸ (1 ̸ 3)² + y² ̸ (1 ̸ 6)² - z² ̸ (1 ̸ 2)² = 1 на интервале х,y ∊ [-5;4,5] с шагом 0.5 ;
ІV Вариант. x² ̸ 9 + y² ̸ 4 - z² = -1 на интервале х ∊ [-3;3] с шагом 0.5, y∊[-2;2] с шагом 1.

Самостоятельная работа