Слайд 108/16/2019
Задачи изучения дисциплины:
изучение общих свойств волновых движений различной природы;
ознакомление с классификацией волн и сред их распространения;
изучение математических
моделей электромагнитных и акустических волн, электрических волн в длинных линиях;
изучение законов дисперсии различных волновых процессов и связанных с ними особенностей распространения волн;
изучение законов распространения волновых пакетов в линейных средах;
освоение методов решения линейных волновых уравнений для основных типов объемных и поверхностных волн и волн в направляющих системах;
изучение собственных акустических и оптических мод анизотропных сред;
изучение законов распространения волн в слоистых средах;
изучение основных типов взаимодействия волн различной природы в линейных и нелинейных средах;
изучение самовоздействия волновых пакетов в нелинейных средах;
изучение основных типов излучателей акустических и электромагнитных волн;
изучение распространения радиоволн вблизи поверхности земли;
изучение эффекта Доплера.
Слайд 208/16/2019
Основная литература
И. Е. Иродов. Волновые процессы. Основные законы:
М.: БИНОМ. Лаборатория знаний, 2006. – 263 с. (100 экз.).
Б. М. Петров Электродинамика и распространение радиоволн. М.: Горячая линия- Телеком, 2003. – 558 с. (133 экз.)
Л. А. Боков. Электромагнитные поля и волны. Томск: ТУСУР, 2003. - 213 с. (44 экз.)
Л. А. Вайнштейн. Электромагнитные волны. М.: Радио и связь, 1988. - 440 с. (16 экз.)
А. И. Козлов, А. И. Логвин, В. А. Сарычев. Поляризация радиоволн. Поляризационная структура радиолокационных сигналов. М.: Радиотехника, 2005. - 702 c. (20 экз.)
Л. Ф. Лепендин. Акустика: М.: Высшая школа, 1978. - 447 с. (15 экз.)
Н. И. Калитеевский. Волновая оптика. СПб.: Лань, 2006. – 465 с. (30 экз.)
Т. И. Трофимова, А. В. Фирсов. Курс физики. Колебания и волны: Теория, задачи и решения. - М.: Академия, 2003. (70 экз.)
Слайд 308/16/2019
Дополнительная литература
Ф. С. Крауфорд Волны. М.: Наука, 1984. -
509 с.
Ф. Сьярли. Математическая теория упругости. М.: Мир, 1992.
– 472 с.
Л. М. Бреховских, О. А. Годин. Акустика слоистых сред. М.: Наука, 1989. – 411 с.
И. А. Викторов. Звуковые поверхностные волны в твердых телах. - М.: Наука, 1981. - 286 с.
М. Б. Виноградова, О. В. Руденко, А. П. Сухоруков. Теория волн. - М.: Наука, 1979. – 383 с.
Дж. Уизем. Линейные и нелинейные волны. М.: Мир, 1977. – 622 с.
М. А. Исакович. Общая акустика: М.: Наука, 1973. - 494 с.
Л. М. Бреховских. Волны в слоистых средах. М.: Наука, 1973. – 343 с.
Г. С. Горелик. Колебания и волны. Введение в акустику, радиофизику и оптику. М.: Физматгиз, 1959. – 572 с.
А. Ляв. Математическая теория упругости. М.: Объединенное научно- техническое издательство НКТП СССР, 1935. – 674 с.
Слайд 408/16/2019
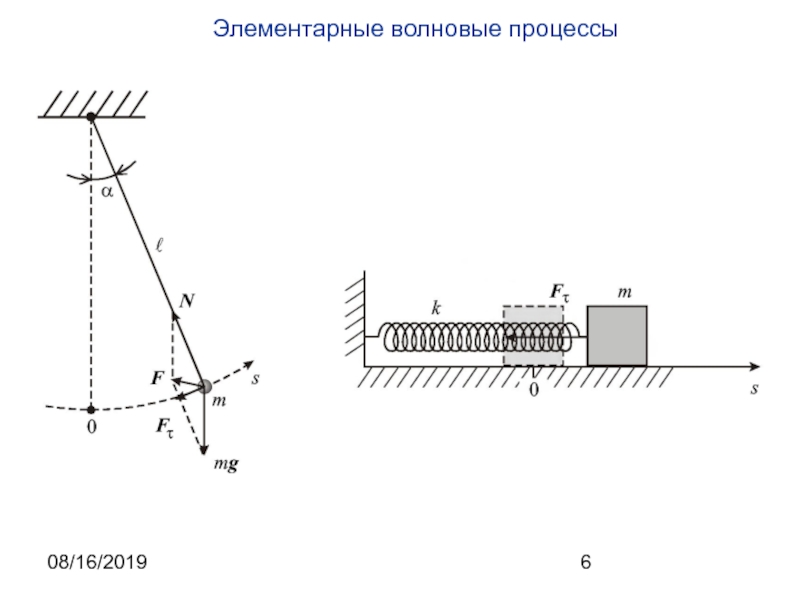
Колебания и волны.
В общем случае колебанием можно назвать процесс, имеющий
определенную периодичность во времени (или в любых других координатах).
Колебания можно
классифицировать по различным признакам:
По числу независимых переменных (обобщенных координат), необходимых для полного описания процессов в колебательной системе. Эти переменные в физике называют степенями свободы.
Линейные и нелинейные. Для линейных систем характерно то, что изменение величины возмущения вызывает лишь количественные изменения мгновенного значения колебаний, пропорциональные величине возмущения. Характерной особенностью линейных колебаний является выполнение принципа суперпозиции для колебаний возникающих под действием многих возмущающих факторов.
В зависимости от того действует ли источник энергии во время колебательного процесса или не действует, колебания подразделяются на вынужденные и свободные.
Слайд 508/16/2019
Если материальные параметры колебательной системы зависят от той или иной
независимой физической величины (например элементы электрической цепи С,L или R
могут зависеть от времени), то колебания называются параметрическими (или не автономными). В противном случае автономными. Часто понятие параметрических колебаний сужают на системы с периодической зависимостью материальных параметров от обобщенных координат.
Общее свойство математических моделей колебательного процесса
Сосредоточенные колебательные процессы описываются одним или несколькими обыкновенными дифференциальными уравнениями.
Слайд 708/16/2019
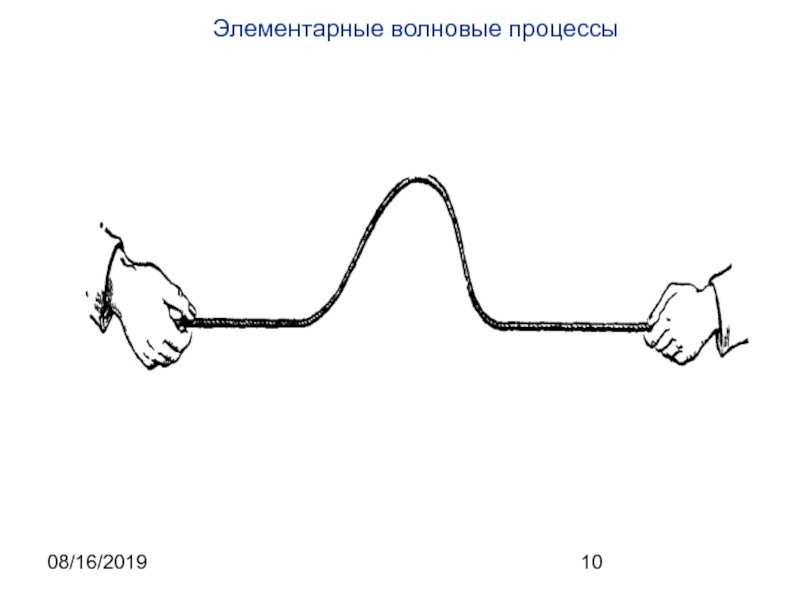
Волна — это распространение колебаний в пространстве, происходящее с конечной
скоростью. Волновой процесс — более сложная модель движения реальных систем,
состояние которых зависит уже не только от времени, но и от пространственных переменных. Поэтому такие процессы описываются уравнениями, содержащими частные производные.
В физике волнами или волной называют всякое изменяющееся со временем пространственное чередование максимумов и минимумов (в том числе локальных) любой физической величины, например плотности вещества напряженности электрического поля, температуры. Волной часто называют также всякое явление, при котором в пространстве происходит распространение кратковременного электрического или механического «толчка». Таким образом, понятие «волна» охватывает весьма обширный круг явлений.
Слайд 1308/16/2019
Критерием перехода от колебательного движения к волновому может служить «условие
квазистационарности»: если характерные размеры системы
L < сТ
(с —
скорость распространения возмущения, Т — время его заметного изменения), о процессе можно говорить как о колебательном в системе с сосредоточенными параметрами: В случае L > сТ процесс нужно считать волновым, а систему — распределенной.
Слайд 1408/16/2019
Значение волн
Волны обычно служат наиболее быстрым механизмом переноса энергии, позволяющим
осуществить в системе переход от неравновесного состояния к равновесному. При
этом не происходит существенного перемещения вещества, хотя такое перемещение иногда возможно как побочное явление, сопровождающее распространение волны.
Волновой процесс - это одна из важнейших форм движения материи; в той или иной мере волновые движения присущи всем без исключения объектам материального мира. Как показали эксперименты по дифракции и рассеянию микрочастиц, корпускулярно-волновой дуализм есть фундаментальное свойство материи вообще, и для описания состояния квантовых систем необходимо пользоваться волновыми функциями.
Слайд 1508/16/2019
Механизмы распространения волновых возмущений различных физических величин, сильно отличаются друг
от друга.
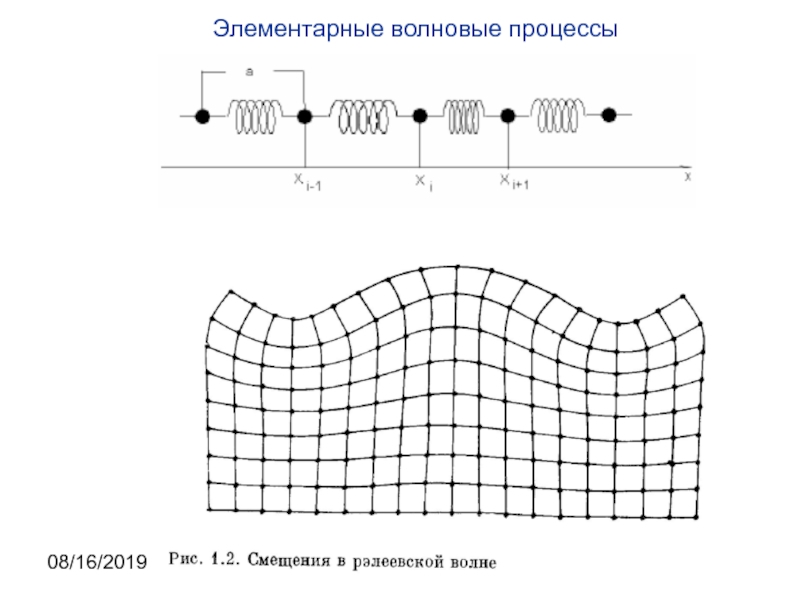
Упругие волны в жидкостях и газах существуют вследствие
того, что коллективное движение частиц среды создает чередующиеся сжатия и разрежения, которые вызывают движение в следующем слое жидкости (газа). Возмущение передается от слоя к слою преимущественно в направлении, вдоль которого происходят колебания частиц, т. е. волны в жидкостях и газах являются продольными.
Твердые тела обладают сдвиговой упругостью, и в них могут распространяться поперечные волны.
Распространение электромагнитных волн происходит вследствие того, что появляющееся в какой-либо точке пространства переменное электрическое поле возбуждает в соседних точках магнитное поле и.наоборот.
Слайд 1608/16/2019
В зависимости от того какая физическая величина находится в состоянии
волнового движения, скалярная, векторная или тензорная, волны принято делить на
скалярные, векторные или тензорные.
Пример
Волна де-Бройля - скалярная волны
Электромагнитная волна – векторная волна
Акустическая волна – векторная волна
Волновые возмущения диэлектрической проницаемости - тензорная волна
Слайд 1708/16/2019
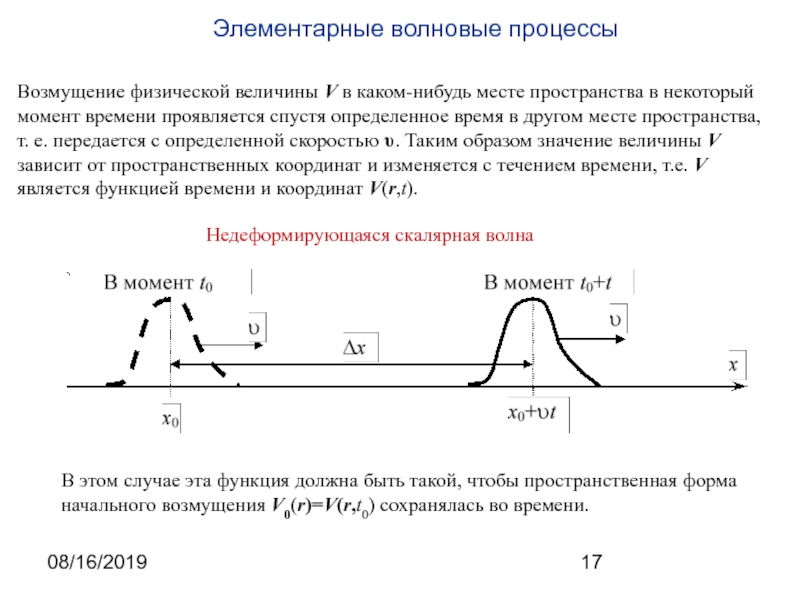
Возмущение физической величины V в каком-нибудь месте пространства в некоторый
момент времени проявляется спустя определенное время в другом месте пространства,
т. е. передается с определенной скоростью υ. Таким образом значение величины V зависит от пространственных координат и изменяется с течением времени, т.е. V является функцией времени и координат V(r,t).
В этом случае эта функция должна быть такой, чтобы пространственная форма начального возмущения V0(r)=V(r,t0) сохранялась во времени.
Недеформирующаяся скалярная волна
Слайд 1808/16/2019
Формула для недеформирующейся волны
Пусть в начальный момент времени V(x=x0,t=t0)=V(x0,t0). По
истечении времени Δt функция примет значения V(x,t)=V(x0+Δx,t0+Δt). Ограничимся малыми приращениями
x0>>Δx и t0>>Δt.
Форма возмущения будет сохраняться при распространении, если ее значение в момент t0 в точке x0 будет равно ее значению в момент t0+Δt в точке x0+Δx. Т.е.
Слайд 1908/16/2019
Вводя обозначения
перепишем условие сохранения формы начального возмущения в виде
В рассматриваемом
случае Δx>0 (Δt>0 в силу свойства времени). Поэтому b/a
раз обозначая ⎜b/a⎜ =υ получим соотношение
связывающее приращения Δx=x–x0 и Δt=t–t0. Из последнего соотношения следует формула
Слайд 2008/16/2019
Таким образом время и координата входят в функцию описывающую волновой
процесс не независимо. Они связаны простым линейным соотношением. Это указывает
на то, что V(x,t) на самом деле является функцией одного аргумента
V(x,t)=V(ξ)=V(x–υt).
Аналогичные рассуждения для волнового процесса, распространяющегося вдоль отрицательного направления оси X показывают, что он описывается функцией вида
V(x+υt).
В случае распространения векторных (или тензорных волн полученные результаты могут быть применены к каждой компоненте вектора
V(x,t)={Vi(x–υit)} (тензора V(x,t)={Vi,j,k…(x–υi,j,k…t)}).
Слайд 2108/16/2019
Монохроматические волны
Широко известными являются волновые процессы с периодической гармонической временной
зависимостью, которая, в соответствии с методом комплексных амплитуд, может быть
описана при помощи пропагатора
exp[iωt],
где ω – частота.
Тогда функция волнового процесса имеет вид
V(x–υt)=F(x)exp(iωt).
Равенство может быть выполнено, если пространственная часть F(x) функции будет пропорциональна
exp(px) (F(x)∝ exp(px)).
Слайд 2208/16/2019
Тогда
V(x–υt)=Aexp(px)exp(iωt)=Aexp(iωt+px),
где A некоторая, в общем случае комплексная постоянная
(амплитуда). Последнее соотношение оказывается справедливым, если p=–ik. Тогда легко получить
следующую формулу
Слайд 2308/16/2019
Фаза волны
В рассматриваемом случае фаза является элементарной линейной функцией
В момент
времени t0 поставим «маркер» на фазе φ0 в некоторой точке
x0 и будем следить за перемещение этой фазой с течением времени. По истечении времени промежутка времени Δt эта фаза окажется в точке
Таким образом волновой процесс можно рассматривать с точки зрения перемещения фазы физической величины. Если описывается волновой процесс распространяющийся вдоль некоторой прямой, то геометрическим местом (фигурой) равной фазы является точка.
Слайд 2608/16/2019
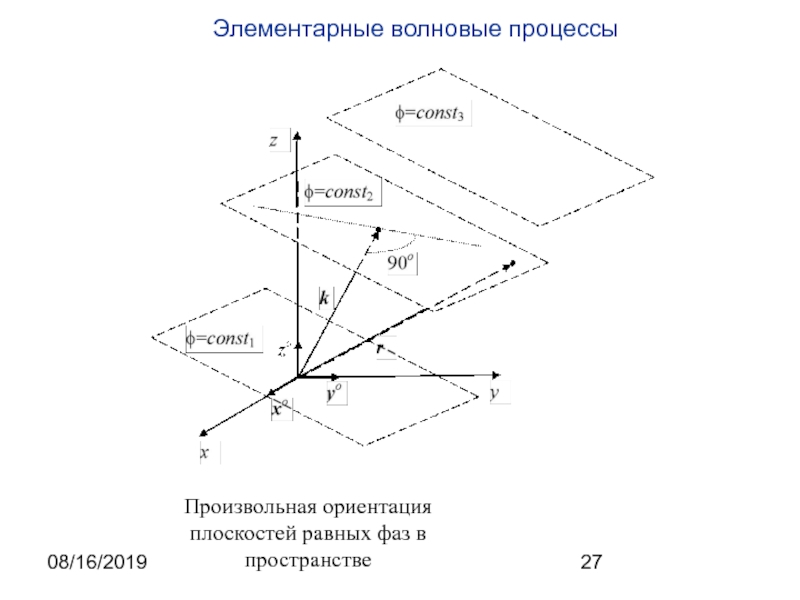
В случае плоской волны (в том числе и векторной), распространяющейся
в произвольном направление, не совпадающем не с одной из координатных
осей
где A – векторная амплитуда волны,
Слайд 2808/16/2019
Цилиндрические и сферические волны
Существуют другие типы волн, которые могут быть
описаны выражением
где
скалярные вещественные функции с векторным аргументом
Слайд 3008/16/2019
Цилиндрические волны, для случая kρ>>1, где ρ – расстояние от
оси волнового фронта, описываются соотношением
Сферические волны, для случая kr>>1,
где r – расстояние от центра волнового фронта, описываются соотношением