Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение сечений тетраэдра и параллелепипеда
Содержание
- 1. Построение сечений тетраэдра и параллелепипеда
- 2. Содержание:Цели и задачи.Введение.Понятие секущей плоскости.Определение сечения.Правила построения
- 3. Развитие пространственных представлений у учащихся.Познакомить с правилами
- 4. Для решения многих геометрических задач необходимо строить их сечения различными плоскостями.
- 5. Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость,
- 6. Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по
- 7. При этом необходимо учитывать следующее:1. Соединять можно
- 8. Какие многоугольники могут получиться в сечении ?Тетраэдр имеет 4 граниВ сечениях могут получиться:ЧетырехугольникиТреугольники
- 9. ТреугольникиПараллелепипед имеет 6 гранейЧетырехугольники ШестиугольникиПятиугольникиВ его сечениях могут получиться:
- 10. Построить сечение тетраэдра DABC плоскостью, проходящей через
- 11. Построить сечение тетраэдра плоскостью, проходящей через точки
- 12. Построить сечение тетраэдра плоскостью, проходящей через точки
- 13. EFLABCDОПостроить сечение тетраэдра плоскостью, проходящей через точки E, F, K.KПервый способПравила
- 14. Вывод: независимо от способа построения сечения одинаковые.Способ №1.Способ №2.
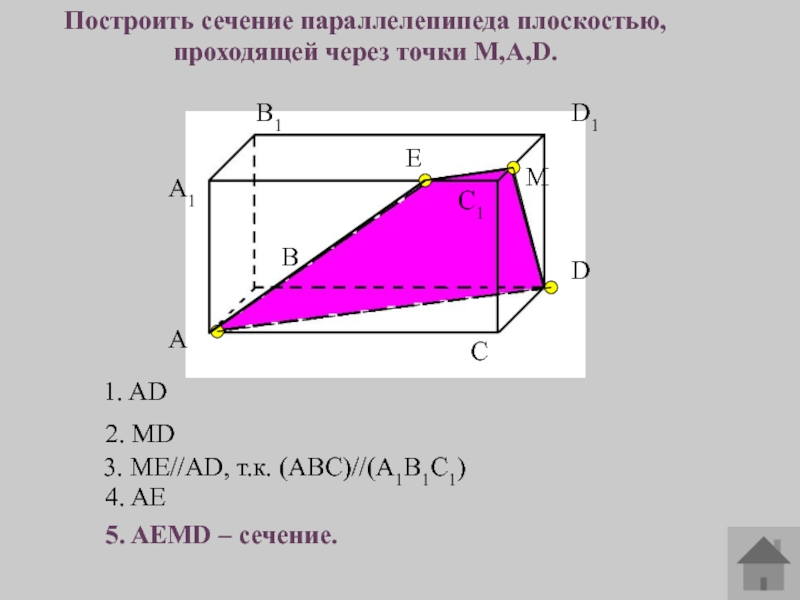
- 15. A1АВВ1СС1DD1MNПостроить сечения параллелепипеда плоскостью, проходящей через точки
- 16. A1АВВ1СС1DD1Построить сечение параллелепипеда плоскостью, проходящей через точки
- 17. ВЫ МНОГОЕ УЗНАЛИИ МНОГОЕ УВИДЕЛИ!ТАК ВПЕРЕД, РЕБЯТА:ДЕРЗАЙТЕ И ТВОРИТЕ!СПАСИБО ЗА ВНИМАНИЕ.
- 18. Скачать презентанцию
Содержание:Цели и задачи.Введение.Понятие секущей плоскости.Определение сечения.Правила построения сечений.Виды сечений тетраэдра.Виды сечений параллелепипеда.Задача на построение сечения тетраэдра с объяснением.Задача на построение сечения тетраэдра с объяснением.Задача на построение сечения тетраэдра по наводящим вопросам.Второй
Слайды и текст этой презентации
Слайд 1Построение сечений тетраэдра и параллелепипеда.
© Ткачева Виктория Викторовна,
учитель математики школы
№ 183 с углубленным изучением английского языка.
Слайд 2Содержание:
Цели и задачи.
Введение.
Понятие секущей плоскости.
Определение сечения.
Правила построения сечений.
Виды сечений тетраэдра.
Виды
сечений параллелепипеда.
Задача на построение сечения тетраэдра с объяснением.
Задача на построение
сечения тетраэдра с объяснением.Задача на построение сечения тетраэдра по наводящим вопросам.
Второй вариант решения предыдущей задачи.
Задача на построение сечения параллелепипеда.
Задача на построение сечения параллелепипеда.
Пожелание учащимся.
Слайд 3Развитие пространственных представлений у учащихся.
Познакомить с правилами построения сечений.
Выработать навыки
построения сечений тетраэдра и параллелепипеда при различных случаях задания секущей
плоскости.Сформировать умение применять правила построения сечений при решении задач по темам «Многогранники».
Цель работы:
Задачи:
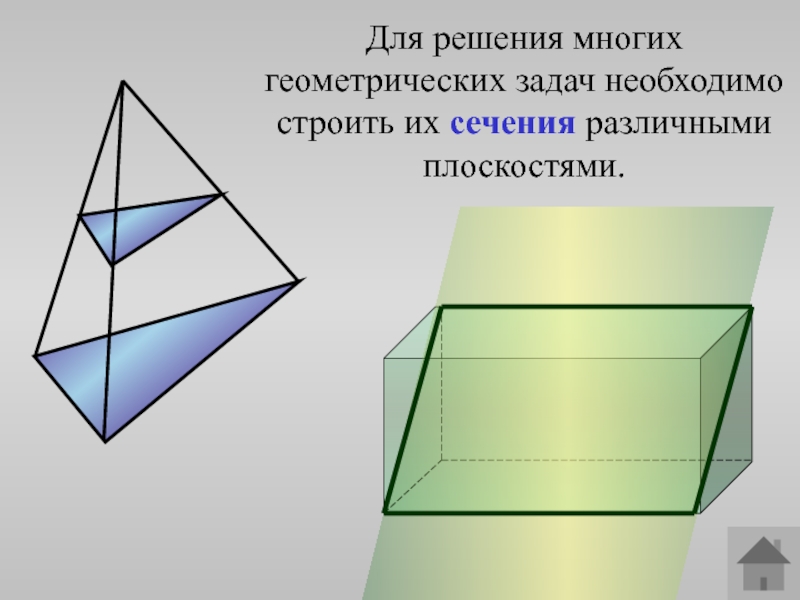
Слайд 4Для решения многих геометрических задач необходимо строить их сечения различными
плоскостями.
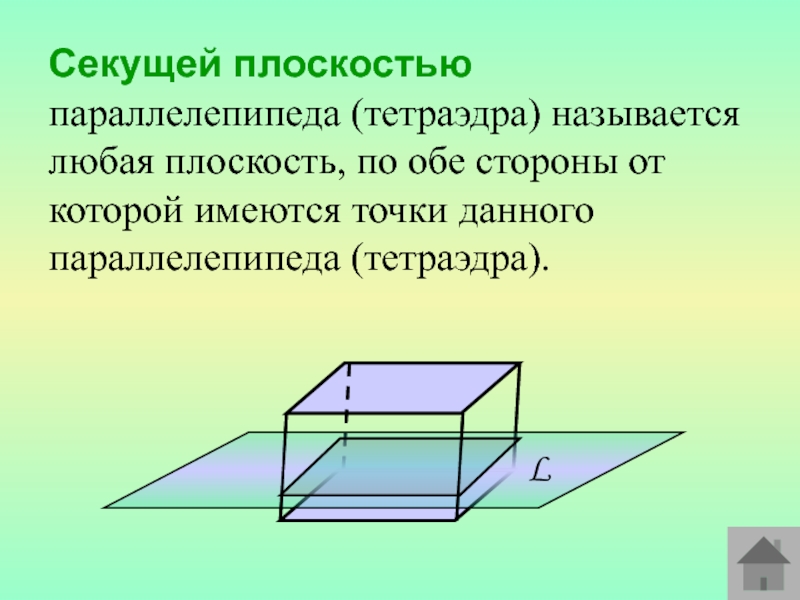
Слайд 5Секущей плоскостью параллелепипеда (тетраэдра) называется любая плоскость, по обе стороны
от которой имеются точки данного параллелепипеда (тетраэдра).
Слайд 6Секущая плоскость пересекает грани тетраэдра (параллелепипеда) по отрезкам.
Многоугольник, сторонами которого
являются данные отрезки, называется сечением тетраэдра (параллелепипеда).
Слайд 7При этом необходимо учитывать следующее:
1. Соединять можно только две точки,
лежащие
в плоскости одной грани.
Для построения сечения нужно построить точки пересечения
секущей плоскости с ребрами и соединить их отрезками.2. Секущая плоскость пересекает параллельные грани по параллельным отрезкам.
3. Если в плоскости грани отмечена только одна точка, принадлежащая плоскости сечения, то надо построить дополнительную точку. Для этого необходимо найти точки пересечения уже построенных прямых с другими прямыми, лежащими в тех же гранях.
Слайд 8Какие многоугольники могут получиться в сечении ?
Тетраэдр имеет 4 грани
В
сечениях могут получиться:
Четырехугольники
Треугольники
Слайд 9Треугольники
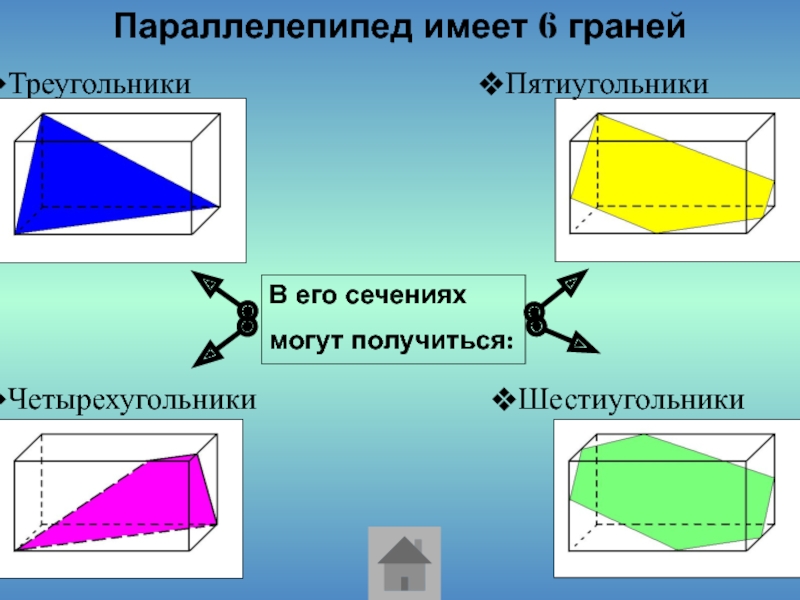
Параллелепипед имеет 6 граней
Четырехугольники
Шестиугольники
Пятиугольники
В его сечениях
могут получиться:
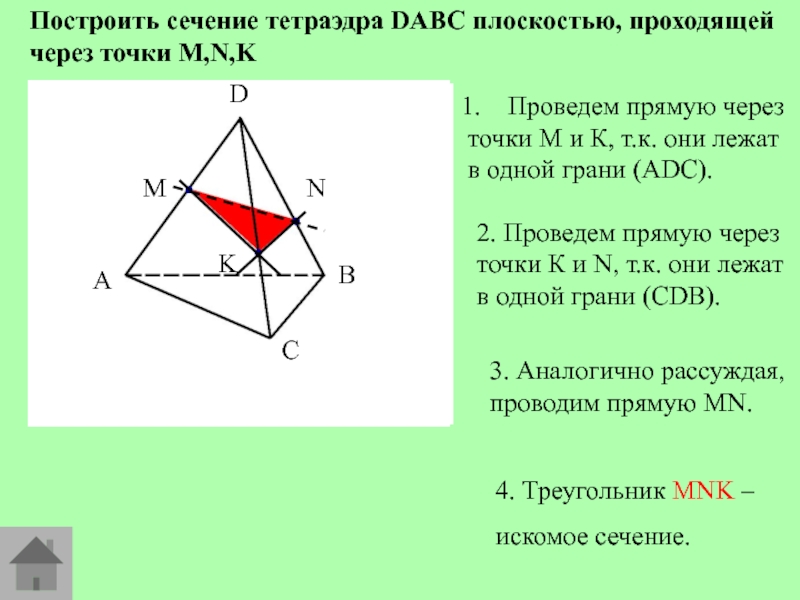
Слайд 10Построить сечение тетраэдра DABC плоскостью, проходящей через точки M,N,K
Проведем прямую
через
точки М и К, т.к. они лежат
в одной
грани (АDC).2. Проведем прямую через точки К и N, т.к. они лежат в одной грани (СDB).
3. Аналогично рассуждая, проводим прямую MN.
4. Треугольник MNK –
искомое сечение.
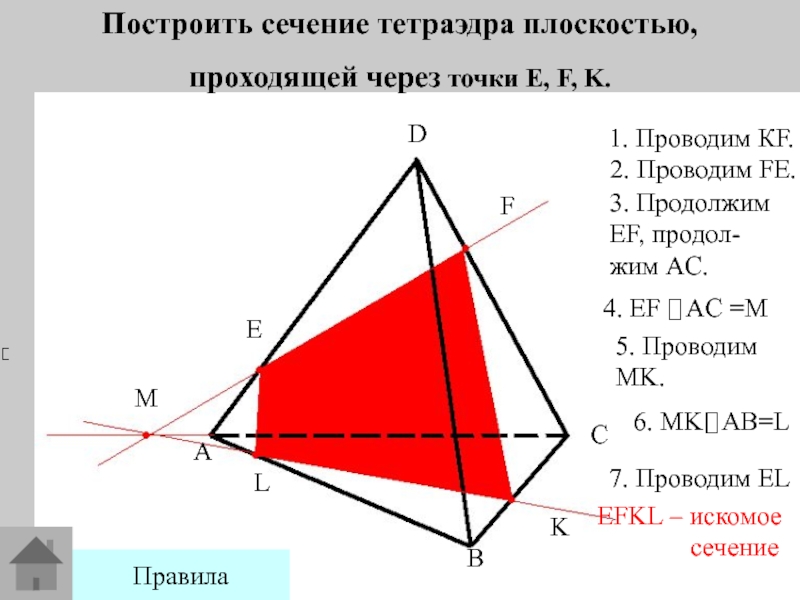
Слайд 11Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
E
F
K
L
A
B
C
D
M
1.
Проводим КF.
2. Проводим FE.
3. Продолжим EF, продол- жим AC.
5. Проводим
MK.7. Проводим EL
EFKL – искомое
сечение
Правила
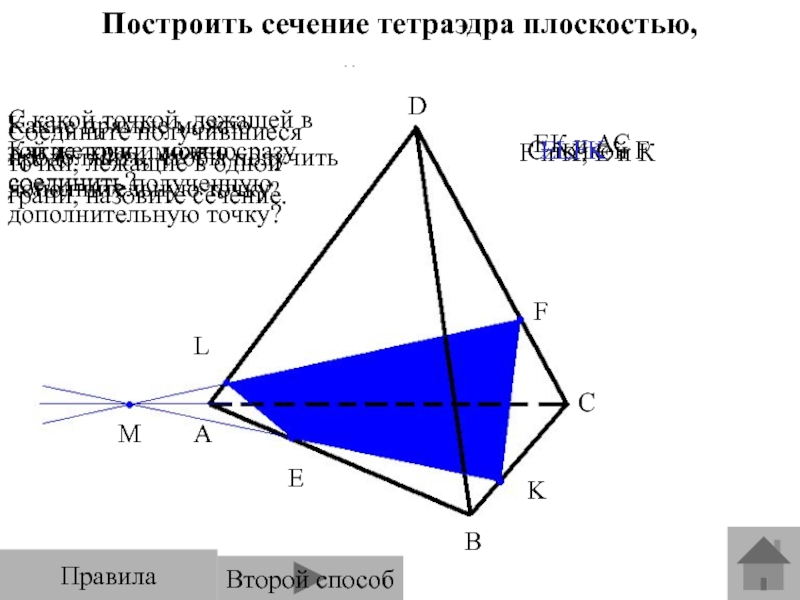
Слайд 12Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
E
F
K
L
A
B
C
M
D
Какие
точки можно сразу соединить?
С какой точкой, лежащей в той же
грани можно соединить полученную дополнительную точку?Какие прямые можно продолжить, чтобы получить дополнительную точку?
F и K, Е и К
ЕК и АС
С точкой F
Соедините получившиеся точки, лежащие в одной грани, назовите сечение.
ЕLFK
Правила
Второй способ
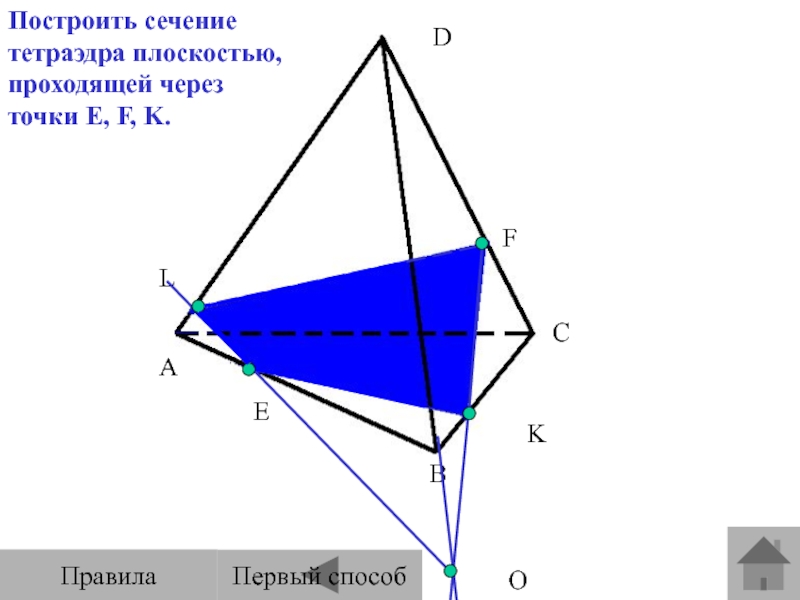
Слайд 13E
F
L
A
B
C
D
О
Построить сечение тетраэдра плоскостью,
проходящей через точки E, F, K.
K
Первый
способ
Правила
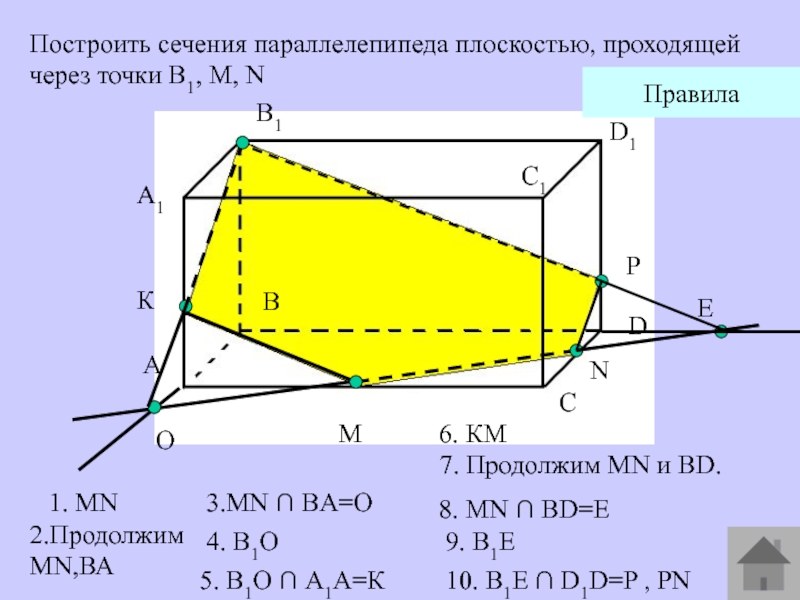
Слайд 15A1
А
В
В1
С
С1
D
D1
M
N
Построить сечения параллелепипеда плоскостью, проходящей через точки В1, М, N
O
К
Е
P
Правила
1. MN
2.Продолжим MN,ВА
4. В1О
6. КМ
7. Продолжим MN и
BD.9. В1E
5. В1О ∩ А1А=К
8. MN ∩ BD=E
10. B1Е ∩ D1D=P , PN
3.MN ∩ BA=O
Слайд 16A1
А
В
В1
С
С1
D
D1
Построить сечение параллелепипеда плоскостью,
проходящей через точки M,A,D.
М
1. AD
2. MD
3.
ME//AD, т.к. (ABC)//(A1B1C1)
4. AE
5. AEMD – сечение.
E
