Поток векторного поля

Содержание

1. Поток векторного поля
2. Слайд 2
3. Слайд 3
4. Слайд 4
5. Слайд 5
6. Если оказывается удобным проектировать поверхность S на
7. Слайд 7
8. Слайд 8
9. Слайд 9
10. Слайд 10
11. Слайд 11
12. Слайд 12
13. Слайд 13
14. Задача 1. Найти поток вектора а =i
15. Задача 2. Вычислить поток векторного поля а
16. На верхнем основании σ2 нормаль n0 параллельна
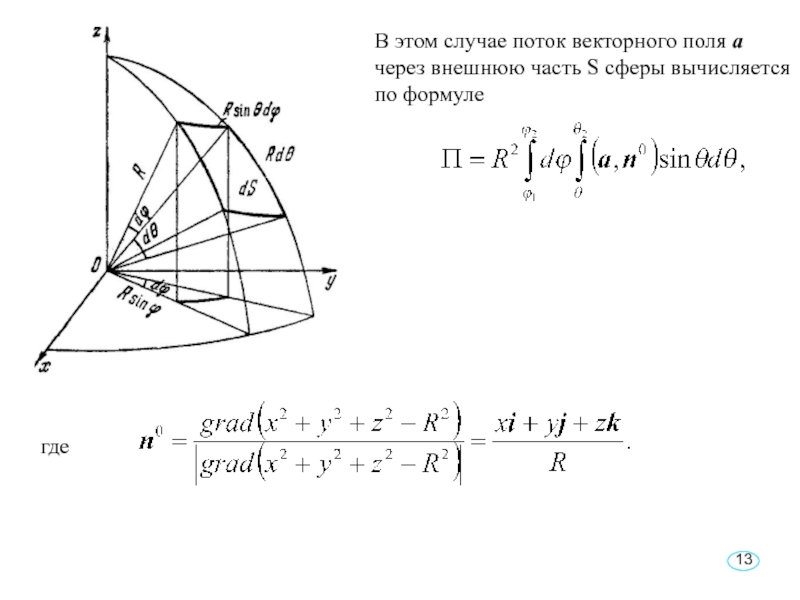
17. Решение. Так как нормаль n к сфере
18. Искомый поток П будет равенТак как площадь сферы
19. Решение. Уравнение плоскости, в которой лежит треугольник
20. Найдем скалярное произведениеВычислим искомый поток
21. Слайд 21
22. Скачать презентанцию

Если оказывается удобным проектировать поверхность S на координатные плоскости yOz или xOz, то для вычисления потока П пользуются соответственно формулами:(4)или(5)Формула (4) применяется в случае, когда поверхность S проектируется взаимно однозначно в

Главная
Разное
Поток векторного поля

Слайды и текст этой презентации

Слайд 1

Слайд 2

Слайд 3

Слайд 4

Слайд 5

Слайд 6Если оказывается удобным проектировать поверхность S на координатные плоскости yOz

или xOz, то для вычисления потока П пользуются соответственно формулами:
(4)
или
(5)
Формула

(4) применяется в случае, когда поверхность S проектируется взаимно однозначно в область Dyz плоскости yOz, а значит, ее можно задать уравнением x=φ(y,z); cosα находится как коэффициент при орте i в формуле

Если оказывается удобным проектировать поверхность S на координатные плоскости yOz или xOz, то для вычисления потока П

Слайд 7

Слайд 8

Слайд 9

Слайд 10

Слайд 11

Слайд 12

Слайд 13

Слайд 14Задача 1.
Найти поток вектора а =i через площадку, перпендикулярную

оси Ох, имеющую форму прямоугольника со сторонами, равными 1 и

2 (см. рис.), в положительном направлении оси Ох.

Решение. Согласно определению потока вектора через поверхность S, будем иметь

В нашем случае а=i, п0 =i, так что

Замечание. Выбрав единичный вектор (орт) нормали к площадке S так, что n0= – i, получили бы П = –2.

Учитывая то, что площадь прямоугольника равна 2, получим

Задача 1. Найти поток вектора а =i через площадку, перпендикулярную оси Ох, имеющую форму прямоугольника со сторонами,

Слайд 15Задача 2.
Вычислить поток векторного поля а = r, где

r — радиус-вектор, через прямой круговой цилиндр с высотой h,

радиусом основания R и осью Оz.

Решение. Поверхность S состоит из боковой поверхности σ1, верхнего основания σ2 и нижнего основания σ3 цилиндра.

Искомый поток П в силу свойства аддитивности будет равен

где П1, П2, П3 — потоки данного поля через σ1, σ2, σ3 соответственно.
На боковой поверхности σ1 цилиндра внешняя нормаль n0 параллельна плоскости хОу, и поэтому

Задача 2. Вычислить поток векторного поля а = r, где r — радиус-вектор, через прямой круговой цилиндр

Слайд 16На верхнем основании σ2 нормаль n0 параллельна оси и поэтому

можно положить п0 = k. Тогда
На нижнем основании σ3 вектор

а =r перпендикулярен к нормали n0 = -k. Поэтому

На верхнем основании σ2 нормаль n0 параллельна оси и поэтому можно положить п0 = k. ТогдаНа нижнем

Слайд 17Решение. Так как нормаль n к сфере коллинеарна радиусу-вектору r,

то можно взять
Но на сфере S имеем |r| = R,

значит

Решение. Так как нормаль n к сфере коллинеарна радиусу-вектору r, то можно взятьНо на сфере S имеем

Слайд 18Искомый поток П будет равен
Так как площадь сферы

Слайд 19Решение. Уравнение плоскости, в которой лежит треугольник АВС, имеет вид

x+y+z=1, откуда z=1-x-y.
Треугольник АВС проектируется взаимно однозначно на плоскость xOy

в область Dxy, которой является треугольник ОАВ.
По условию нормаль n0 к плоскости, в которой лежит треугольник АВС, образует острый угол γ с осью Oz, поэтому