Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Поверхности вращения
Содержание
- 1. Поверхности вращения
- 2. П В общего видаФ(а, i)F1Θ1K1K2i2Ось (i)Произвольная точка
- 3. П В общего видаF1Θ1Меридиональные плоскости – через
- 4. П В, образованные вращением линииПрямой круговой конусГиперболоид
- 5. iФ(а, i)a ││ iПрямой круговой цилиндрx2 +
- 6. Ф(а, i)a ∩ i = sПрямой круговой
- 7. Ф(а, i)Гиперболоидb2z2 – a2(x2 + y2) =
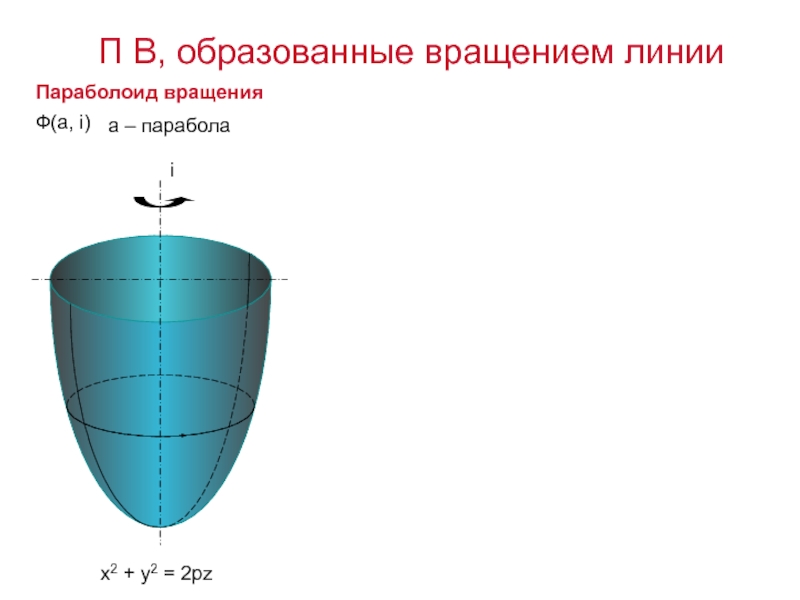
- 8. iПараболоид вращенияx2 + y2 = 2pzФ(а, i)а – парабола П В, образованные вращением линии
- 9. П В, образованные вращением окружностиСфераТор закрытыйТор открытыйt = 0t > Rt > R
- 10. Сфераx2 + y2 + z2 = r2П
- 11. Тор закрытый(x2 + y2 + z2 +
- 12. Тор открытый(x2 + y2 + z2 +
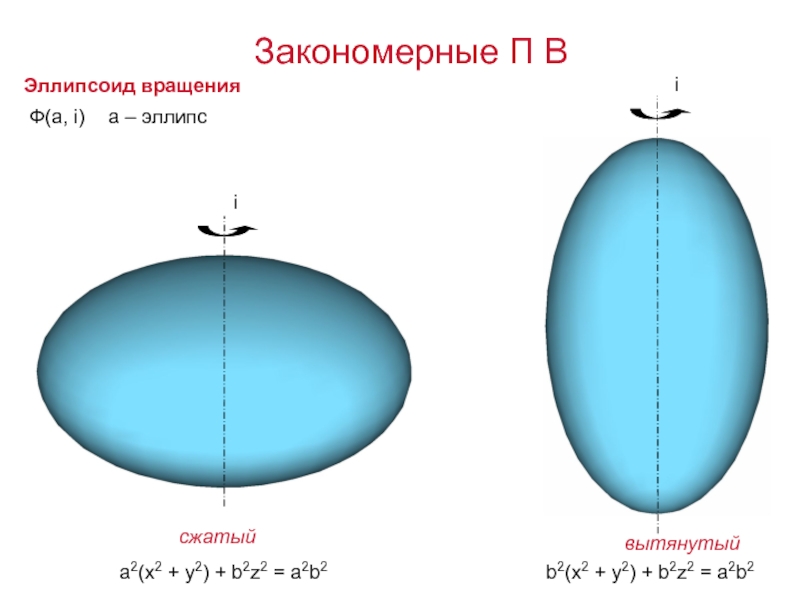
- 13. Эллипсоид вращенияa2(x2 + y2) + b2z2 =
- 14. Скачать презентанцию
П В общего видаФ(а, i)F1Θ1K1K2i2Ось (i)Произвольная точка образующей при вращении вокруг оси описывает окружность – параллель. Радиус параллели – расстояние от точки до оси. Наиб. – экватор, наим. – горловина –
Слайды и текст этой презентации
Слайд 1Поверхности вращения
Поверхность закрытая: меридиональное сечение – замкнутая кривая, пересекающая ось
в 2-х точках
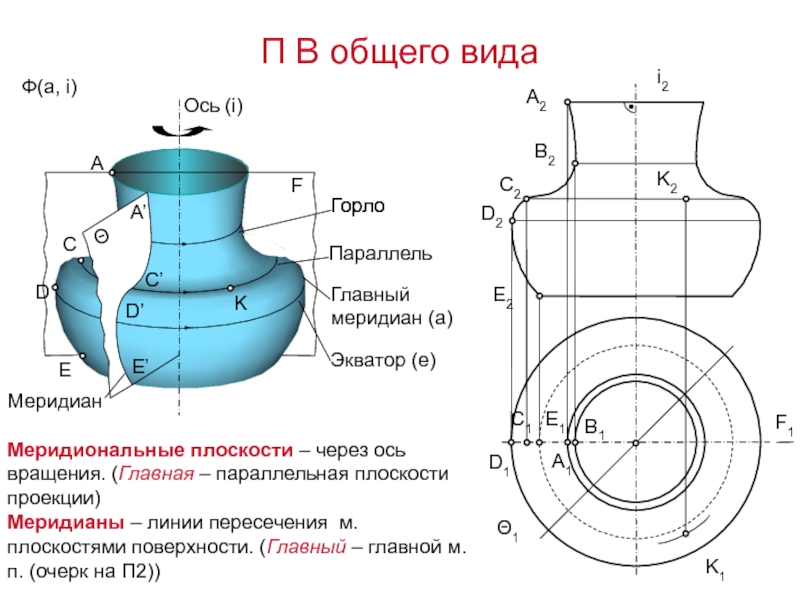
или пространственной кривой) вокруг оси вращения (обычно – горизонтально-проецирующей)
Слайд 2П В общего вида
Ф(а, i)
F1
Θ1
K1
K2
i2
Ось (i)
Произвольная точка образующей при вращении
вокруг оси описывает окружность – параллель.
Радиус параллели – расстояние
от точки до оси. Наиб. – экватор, наим. – горловина – очерковые линии поверхности
i1
A2
B2
C2
D2
E2
E1
C1
D1
B1
A1
A
C
D
E
B
K
Параллель
F
Горло
Главный меридиан (а)
Экватор (е)
Меридиан
B’
C’
D’
E’
Θ
A’
Слайд 3П В общего вида
F1
Θ1
Меридиональные плоскости – через ось вращения. (Главная
– параллельная плоскости проекции)
Меридианы – линии пересечения м. плоскостями поверхности.
(Главный – главной м. п. (очерк на П2))K1
K2
A2
B2
C2
D2
E2
E1
C1
D1
B1
A1
i2
Ф(а, i)
Ось (i)
A
C
D
E
K
Параллель
F
Горло
B’
C’
D’
E’
Θ
A’
Горло
Главный меридиан (а)
Экватор (е)
Меридиан
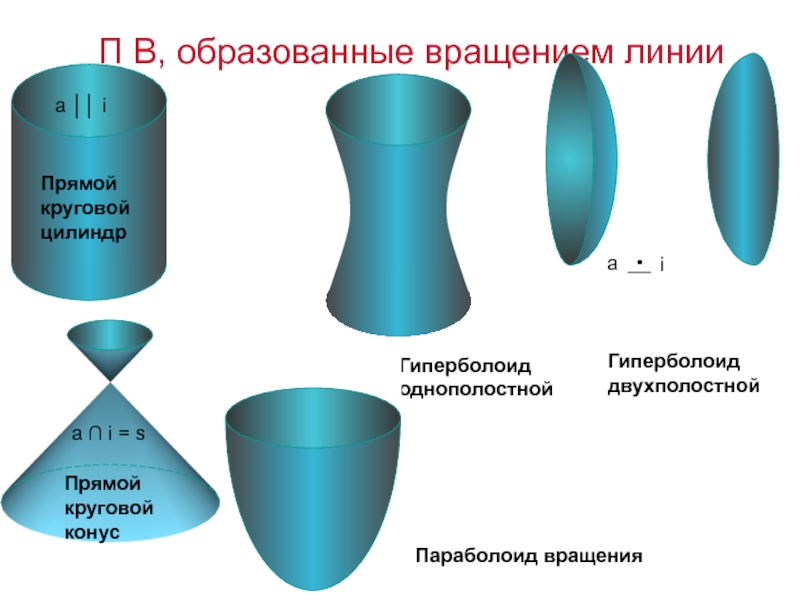
Слайд 4П В, образованные вращением линии
Прямой круговой конус
Гиперболоид однополостной
Параболоид вращения
Гиперболоид двухполостной
Прямой
круговой цилиндр
a ∩ i = s
a ││ i
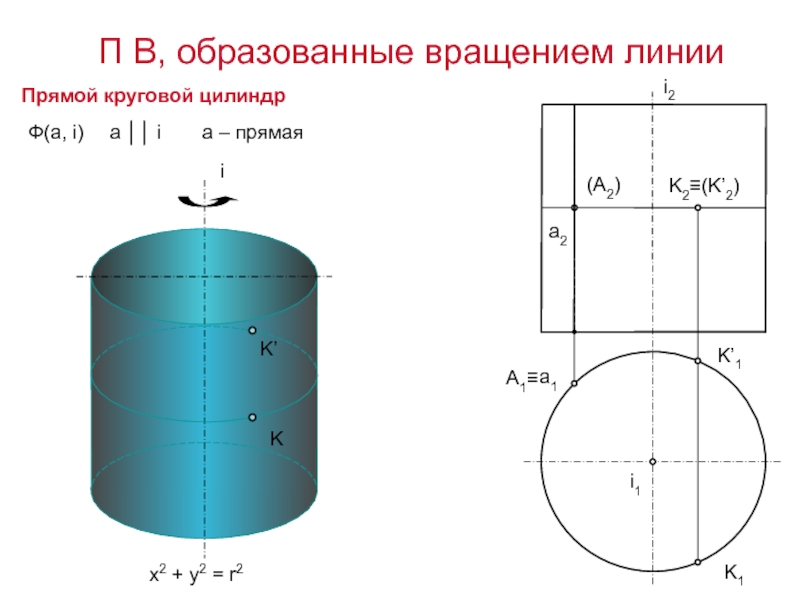
Слайд 5i
Ф(а, i)
a ││ i
Прямой круговой цилиндр
x2 + y2 = r2
а
– прямая
K’1
i2
K2≡(K’2)
a2
(A2)
K1
i1
A1≡
П В, образованные вращением линии
a1
Слайд 6Ф(а, i)
a ∩ i = s
Прямой круговой конус
z2 = k2
(x2 + y2)
а – прямая
K1
K’1
i2
K2≡(K’2)
a1
a2
i1≡S2
S2
i
П В, образованные вращением линии
Слайд 7Ф(а, i)
Гиперболоид
b2z2 – a2(x2 + y2) = a2b2
b2(x2 + y2)
– a2z2 = a2b2
двухполостной
i
а – гипербола
П В, образованные вращением
линииi
однополостной
Слайд 10Сфера
x2 + y2 + z2 = r2
П В, образованные вращением
окружности
Ф(а, i)
а – окружность
t = 0
i
i2
i1
(K1)
(K’1)
K2≡(K’2)
a1
i3
a3
a2
(K’3)
(K3)
0
R
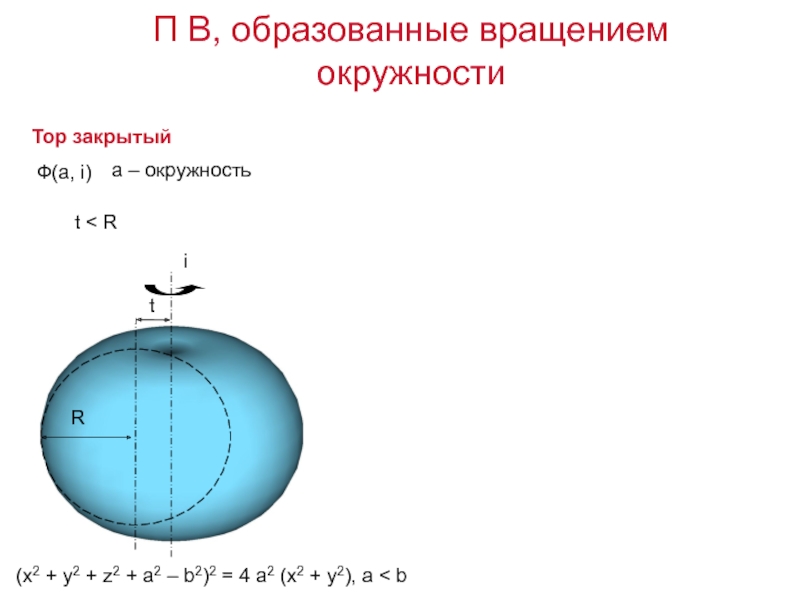
Слайд 11Тор закрытый
(x2 + y2 + z2 + a2 – b2)2
= 4 a2 (x2 + y2), a < b
t
RФ(а, i)
а – окружность
П В, образованные вращением окружности
i
t
0
R
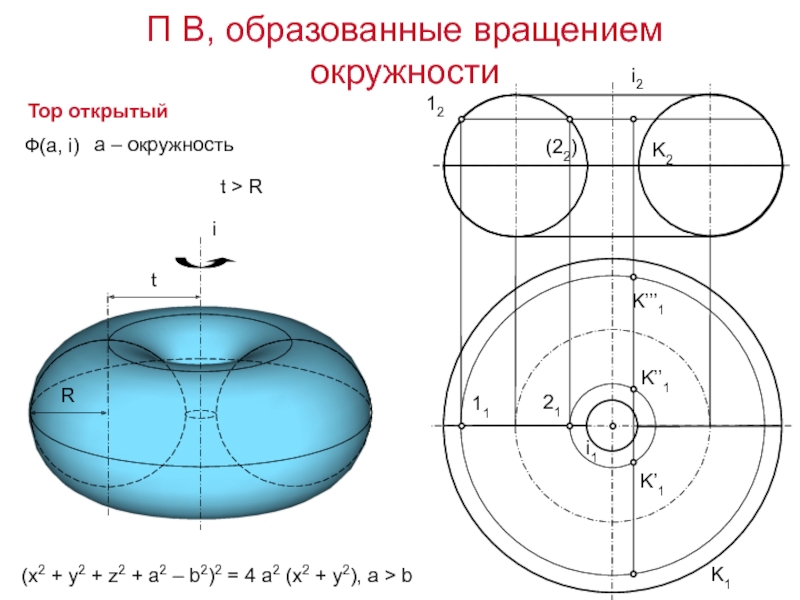
Слайд 12Тор открытый
(x2 + y2 + z2 + a2 – b2)2
= 4 a2 (x2 + y2), a > b
Ф(а, i)
t
> Rt
а – окружность
K’1
i2
K1
i1
K’’1
K’’’1
11
21
12
(22)
K2
П В, образованные вращением окружности
0
i
R
Слайд 13Эллипсоид вращения
a2(x2 + y2) + b2z2 = a2b2
сжатый
вытянутый
b2(x2 + y2)
+ b2z2 = a2b2
Закономерные П В
Ф(а, i)
а – эллипс
i
i
