Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Появление многокритериальности
Содержание
- 1. Появление многокритериальности
- 2. Методы решения многокритер. задач ПРСведения к однокр-ой задачиОптимизация по ПаретоСвертка критериевМетод контр.пок.Выдел.осн.критер
- 3. ПримерПредположим, что приоритет первого критерия – 60%, второго – 40%.
- 4. Множество ПаретоЧто касается точек дуги АВ, то
- 5. Методы решения:Метод уступок.Метод идеальной точки.Метод ограничений.Метод анализа иерархий.
- 6. Пример. Строительство нового аэропорта около города М.
- 7. Оценка многокритериальных альтернатив. Подход аналитической иерархииПостановка задачи:Дано:
- 8. СтруктуризацияЦельКритерииПлощадкиСтроительство аэропортаСтоимость
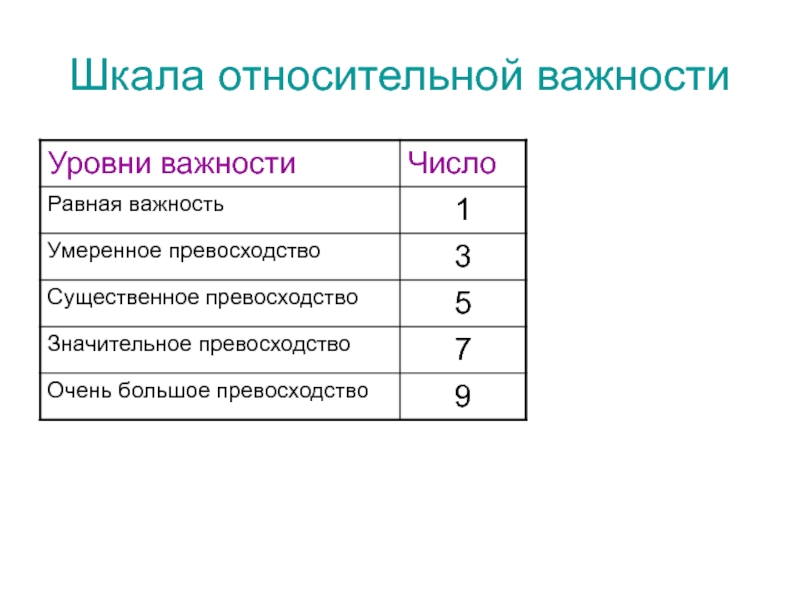
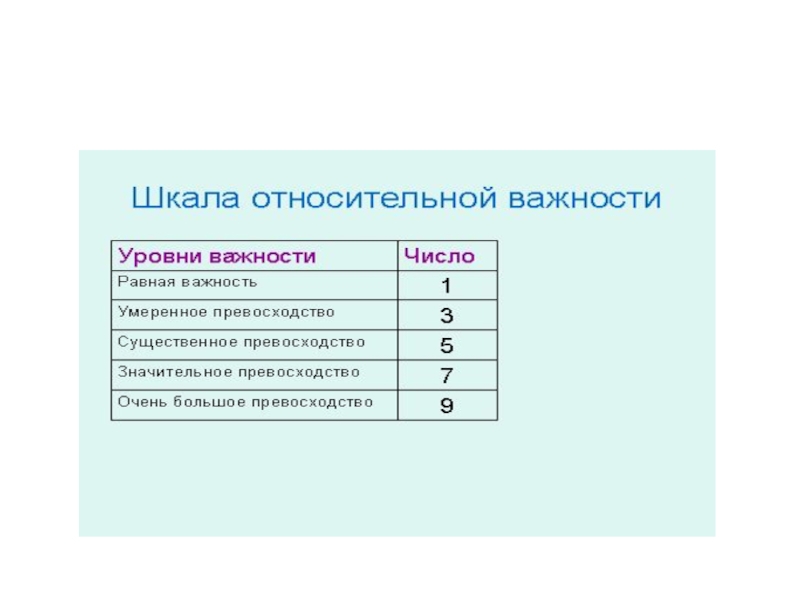
- 9. Шкала относительной важности
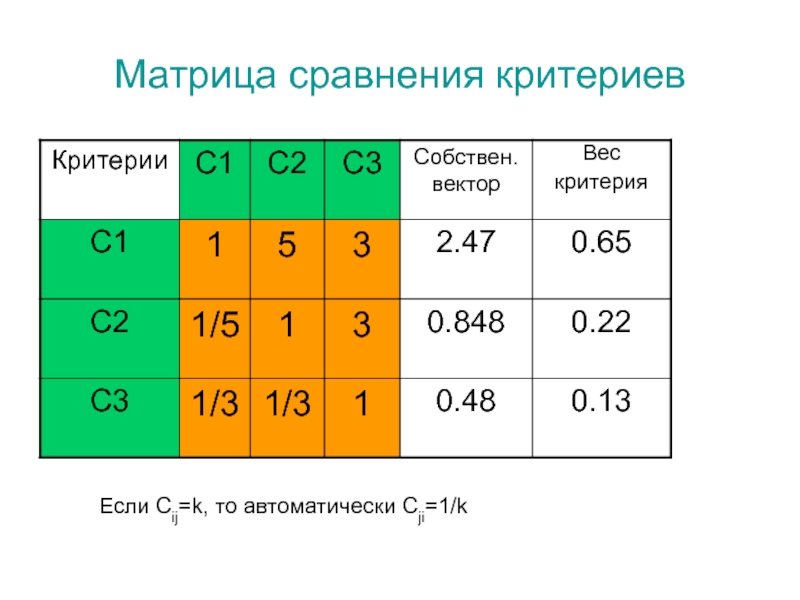
- 10. Матрица сравнения критериевЕсли Сij=k, то автоматически Сji=1/k
- 11. Расчет собственного вектора
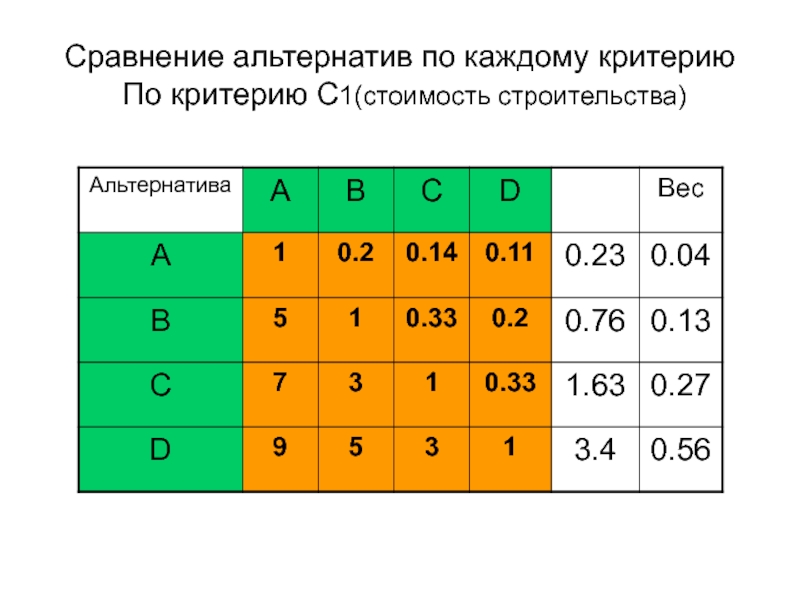
- 12. Сравнение альтернатив по каждому критерию По критерию C1(стоимость строительства)
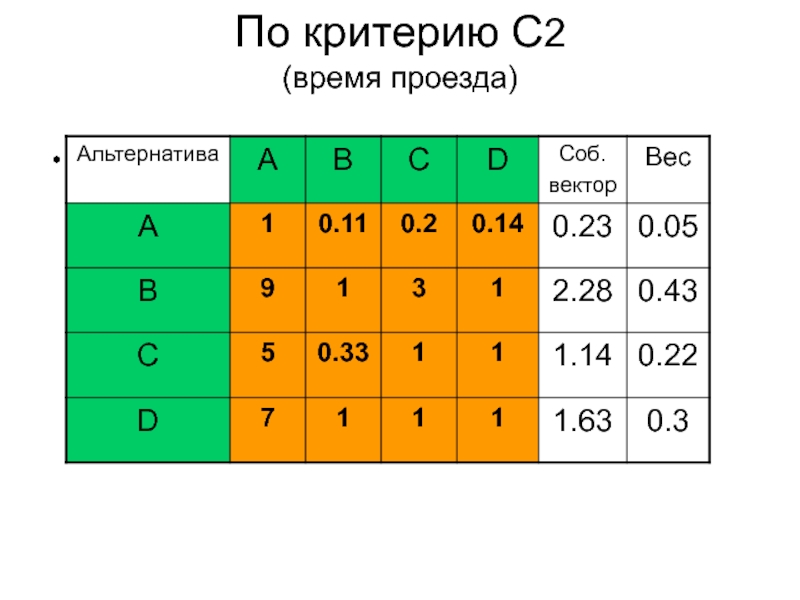
- 13. По критерию С2 (время проезда)
- 14. По критерию С3 (шумовое воздействие)
- 15. Синтез коэффициентов важностиОсуществляется по формуле:
- 16. Выбор площадкиС10.65С20.22С30.13А0.04В0.13С0.27D0.56A0.05B0.43C0.22D0.3A0.56B0.27C0.13D0.04VA=0.65*0.04+ 0.22*0.05+0.13*0.56=0.11VB=0.65*0.13+ 0.22*0.43+0.13*0.27=0.215VC=0.65*0.27+ 0.22*0.22+0.13*0.13=0.241VD=0.65*0.56+ 0.22*0.3+0.13* 0.04=0.431
- 17. Принятие решений в информационных системахОсобый класс задач
- 18. Общие черты неструктуризованных проблемОни являются проблемами уникального
- 19. Качественная модель ЛПР (ЛПР – лицо принимающее
- 20. Классификация проблем ПРВ ТПР принято различать три
- 21. ИзмеренияДо появления весов сравнение предметов по тяжести
- 22. Слайд 22
- 23. Пример: как оценить проекты? ЛПР выделил основные
- 24. Сравнение альтернативK(A1)>k(A2)K(A1)>k(A4)K(A1) N k(A3){k(A1), k(A3)} – эффективное множество{k(A2), k(A4)} – неэффективное множество
- 25. Связь между выбором некоторой альтернативы и
- 26. Примеры1. Путь из пункта А в пункт
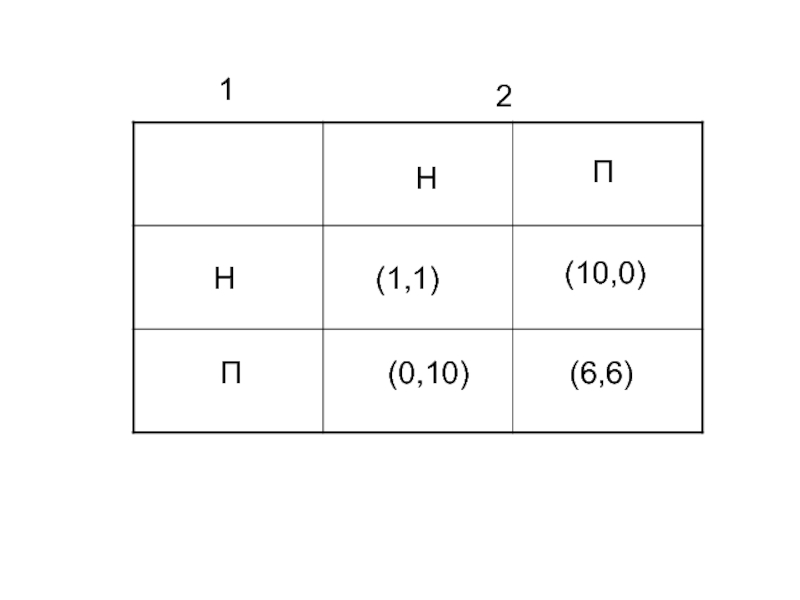
- 27. 1 Н
- 28. Связь альтернатив с исходами при разных типах
- 29. ПримерВо многих случаях лицо ПР, может указать
- 30. Задачи группового выбора решенийНапример. Заседание военного совета.Пусть
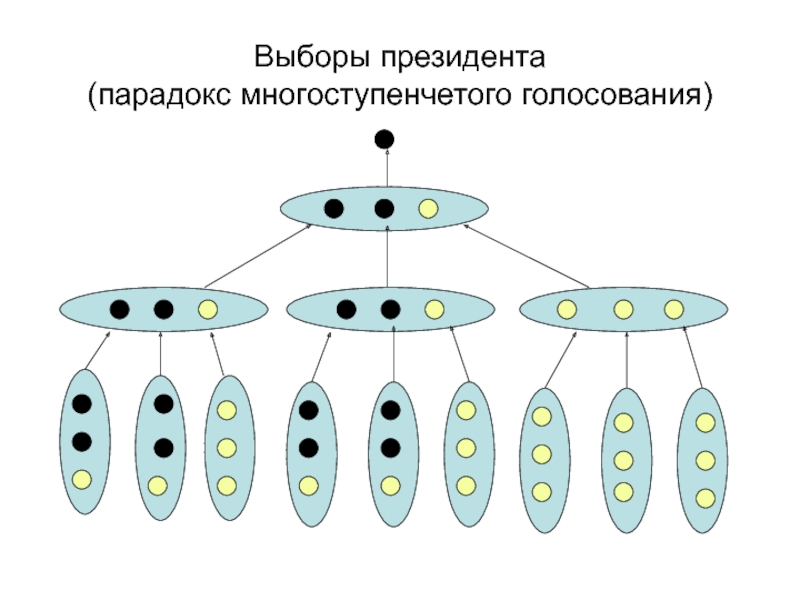
- 31. Выборы президента (парадокс многоступенчетого голосования)
- 32. Основные задачи выбораОдин критерийМного критериевz ZОпределенностьНеопределенность
- 33. Матрица решений в условиях неопределенностиY=F(x,z), F:X
- 34. Критерий Лапласа опирается на принцип, что поскольку
- 35. Критерий принятия решений в условиях полной неопределенностиВ
- 36. далееКритерий минимального сожаления, предложенный Сэвиджем, состоит в
- 37. Пример. Банкет. Число посетителе z1=200, z2=250, z3=300,
- 38. Критерий Сэвиджа приводит к матрице сожалений 0
- 39. Критерий ГурвицаКритерий охватывает ряд различных подходов к
- 40. Критерий ГурвицаВ том случае, когда yij представляет
- 41. Критерий ГурвицаКритерий Гурвица при а=1/2 приводит к выбору решения x*=x1 или x*=x2
- 42. Экспертные системы принятия решенийНазначение и области применения
- 43. Диагностирующие и управляющие системыSЭСУУ ХYS –
- 44. Классы ЭСДиагностирующие системыПрогнозирующие системыПланирующие системыИнтерпретирующие (анализирующие) системы
- 45. Принятие решений в условиях риска (задача о
- 46. продолжениеКаждому состоянию среды zj соответствует вероятность его
- 47. ДалееБудем численно оценивать исход игры по получаемым
- 48. Слайд 48
- 49. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1
Появление многокритериальности
При широком применении методов исследования операций (ИО) аналитики
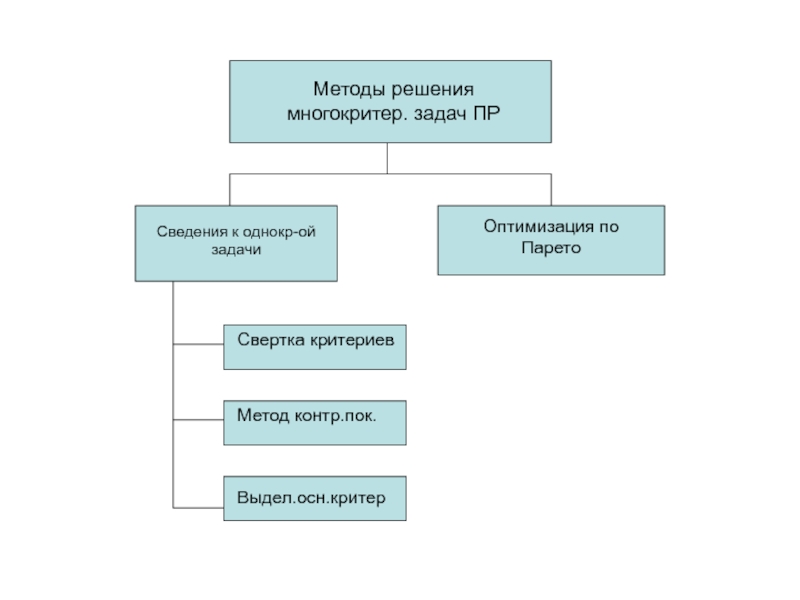
Слайд 2Методы решения многокритер. задач ПР
Сведения к однокр-ой задачи
Оптимизация по Парето
Свертка
критериев
Метод контр.пок.
Выдел.осн.критер
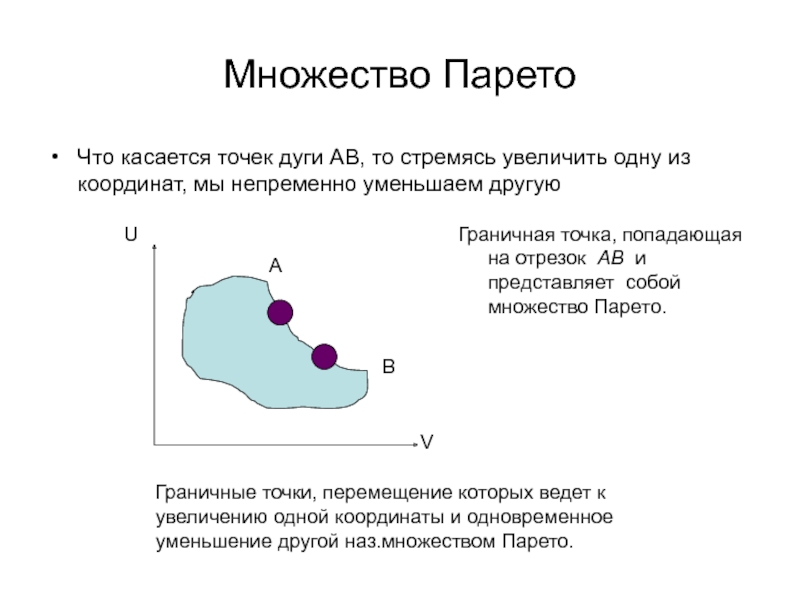
Слайд 4Множество Парето
Что касается точек дуги АВ, то стремясь увеличить одну
из координат, мы непременно уменьшаем другую
U
V
A
B
Граничная точка, попадающая на отрезок
АB и представляет собой множество Парето.Граничные точки, перемещение которых ведет к увеличению одной координаты и одновременное уменьшение другой наз.множеством Парето.
Слайд 6Пример. Строительство нового аэропорта около города М.
Необходимо выбрать площадку.
Критерии:
Стоимость
постройки
Расстояние от города
Минимальное шумовое воздействие
Видно, что все эти критерии противоречивы.
Предположим,
что комиссия отобрала для строительства аэропорта 4 варианта. Площадки A, B, C, D.Для оценки альтернатив используется метод аналитической иерархии.
Слайд 7Оценка многокритериальных альтернатив. Подход аналитической иерархии
Постановка задачи:
Дано: общая цель (или)
цели решения задачи;
Критериев – N, альтернатив – n
Требуется: выбрать наилучшую
альтернативуЭтапы:
Структуризация задачи в виде иерархической структуры с несколькими уровнями: цели – критерии – альтернативы
Далее ЛПР выполняет по парные сравнения элементов каждого уровня. Результаты сравнений переводятся в числа (таблица).
Вычисляются коэф. важности для элементов каждого уровня.
Определяется наилучшая альтернатива.
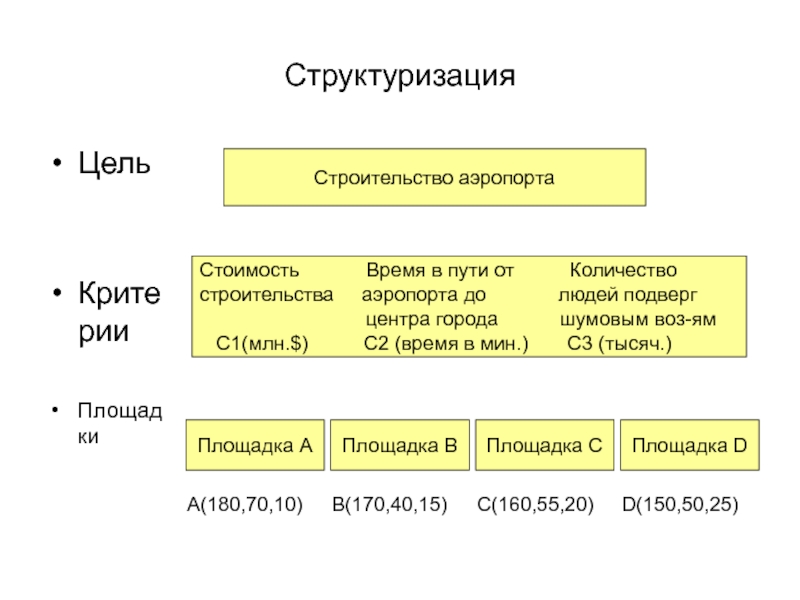
Слайд 8Структуризация
Цель
Критерии
Площадки
Строительство аэропорта
Стоимость Время в пути
от Количество
строительства аэропорта до
людей подвергцентра города шумовым воз-ям
С1(млн.$) C2 (время в мин.) С3 (тысяч.)
Площадка А
Площадка B
Площадка C
Площадка D
A(180,70,10)
B(170,40,15)
C(160,55,20)
D(150,50,25)
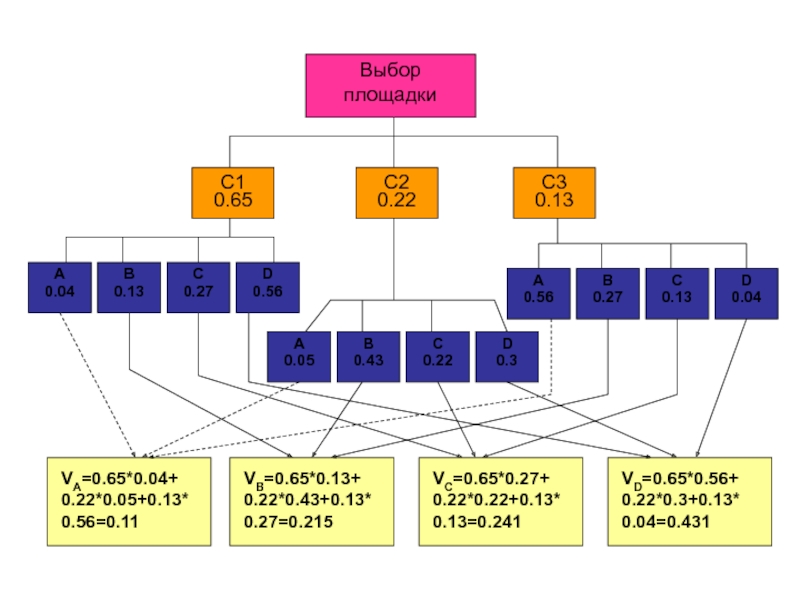
Слайд 16Выбор площадки
С1
0.65
С2
0.22
С3
0.13
А
0.04
В
0.13
С
0.27
D
0.56
A
0.05
B
0.43
C
0.22
D
0.3
A
0.56
B
0.27
C
0.13
D
0.04
VA=0.65*0.04+ 0.22*0.05+0.13*0.56=0.11
VB=0.65*0.13+ 0.22*0.43+0.13*0.27=0.215
VC=0.65*0.27+ 0.22*0.22+0.13*0.13=0.241
VD=0.65*0.56+ 0.22*0.3+0.13* 0.04=0.431
Слайд 17Принятие решений в информационных системах
Особый класс задач ПР:
Неструктуризованные проблемы с
качественными переменными
К неструкт-ым относятся проблемы принятия стратегических решений экономического и
политического характера; проблемы планирования научных исследований и разработок; конкурсного отбора проектов, личные проблемы выбора.В таких проблемах основные характеристики носят качественный характер, трудно поддающиеся формализации, в них отсутствуют достаточно надежные количественные модели.
Слайд 18Общие черты неструктуризованных проблем
Они являются проблемами уникального выбора, как правило
новыми.
Связаны с неопределенностью в оценках альтернатив и нехваткой информации
Оценка альтернатив
носит качественный характер, чаще всего формулируется в словесном (вербальном) виде.Оценки альтернатив по отдельным критериям могут быть получены только от ЛПР и экспертов на основе субъективных предпочтений. При этом отсутствует объективная шкала измерения оценок по отдельным критериям.
Слайд 19Качественная модель ЛПР
(ЛПР – лицо принимающее решение)
ЛПР является
центральным элементом в процессах принятия решений (ПР).
Основные черты ЛПРЧеловек, имеет ограниченный объем кратковременной памяти. Из-за этого он сознательно упрощает ситуацию, превращает часть критериев в ограничения.
Человек не может совершать точные количественные измерения.
Он время от времени совершает ошибки, противоречит сам себе.
Человек вырабатывает правила методом проб и ошибок
Ищет удовлетворительные, а не оптимальные решения.
Минимизирует (подсознательно) свои усилия при поиске решения.
Слайд 20Классификация проблем ПР
В ТПР принято различать три основные задачи:
1. Определение
лучшей альтернативы;
2. Ранжирование альтернатив;
3. Классификация альтернатив (отнесение альтернатив к упорядоченным
классам решений).Эти задачи различаются в двух следующих ситуациях:
Альтернативы заданы на момент ПР (примеры: выбор покупателем товара в магазине, выбор места отдыха, выбор вуза для поступления, выбор места размещения предприятия,
Альтернативы неизвестны или частично известны на момент ПР (примеры: выбор правил проведения конкурсов и отбор лучших проектов; выбор правил поиска квартиры для покупки т.д.)
Слайд 21Измерения
До появления весов сравнение предметов по тяжести осуществлялось с использованием
двух отношений:
E – отношение эквивалентности, L – отношение превосходства.
При
этом существуют условия:E и L исключают друг друга;
Для двух предметов a и b либо aEb, либо aLb, bLa.
Такая схема позволяет производить сопоставление предметов по одному их качеству – весу.
Пример: температура. Прикладывая ладонь к предметам человек совершает относительные измерения (горячо, не чувствует t0, холодно).
Используя такие определения, мы получаем абсолютную порядковую шкалу с дискретными оценками.
Но в некоторых случаях измерения могут быть сделаны только в вербальном виде с использованием сравнения («лучше-хуже», «примерно одинаково»).
В спорте. «хозяева площадки всегда играют лучше чем гости»
Слайд 23Пример: как оценить проекты? ЛПР выделил основные критерии качества проектов со
шкалами возможных значений по ним (оценки по каждому критерию расположены
от лучших к худшим).Критерии оценки проектов
А. Степень проверенности замысла:
1)Созданы единичные изделия;
2)Разработана технология;
3)Предложена идея.
Б. Окупаемость проекта:
1)менее полугода;
2)год;
3)два года и более.
В.Трудности организации производства (при наличии денег):
1)малые;
2)средние;
3)большие.
Г. Наличие спроса на продукт (изделие):
1)большой спрос;
2)достаточный спрос;
3)неопределенный спрос.
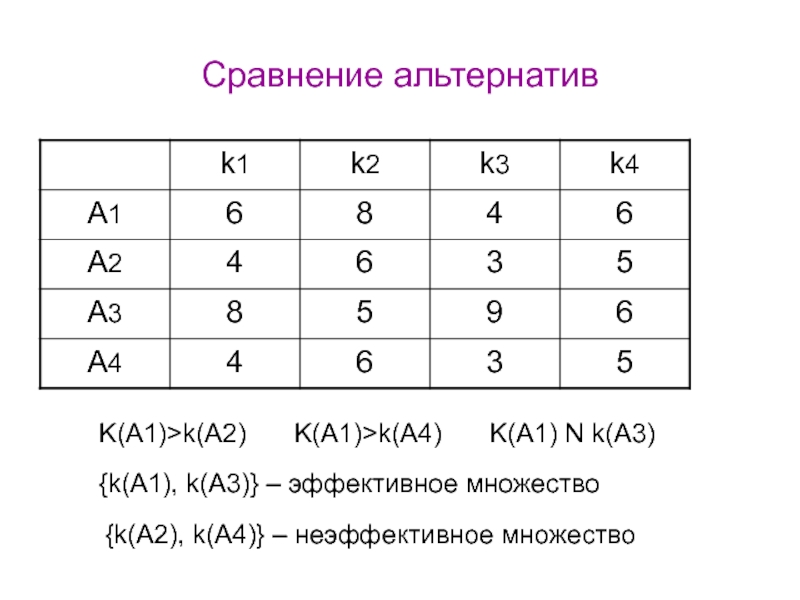
Слайд 24Сравнение альтернатив
K(A1)>k(A2)
K(A1)>k(A4)
K(A1) N k(A3)
{k(A1), k(A3)} – эффективное множество
{k(A2), k(A4)} –
неэффективное множество
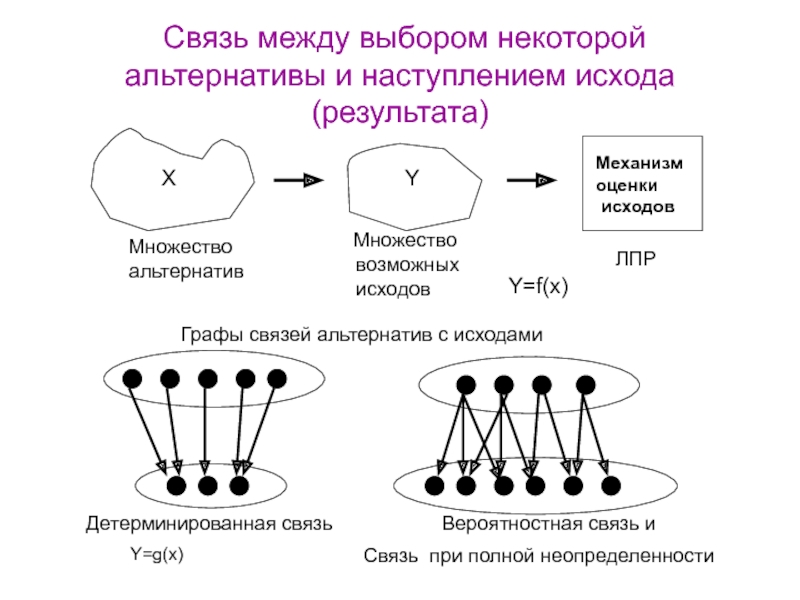
Слайд 25 Связь между выбором некоторой альтернативы и наступлением исхода (результата)
X
Y
Множество альтернатив
Множество
возможных исходов Механизм
оценки исходов
ЛПР
Y=f(x)
Детерминированная связь
Вероятностная связь и
Графы связей альтернатив с исходами
Связь при полной неопределенности
Y=g(x)
Слайд 26Примеры
1. Путь из пункта А в пункт В
2. Студент в
трамвае (брать билет – не брать билет). Вероятн-ый характер.
3. Дилемма
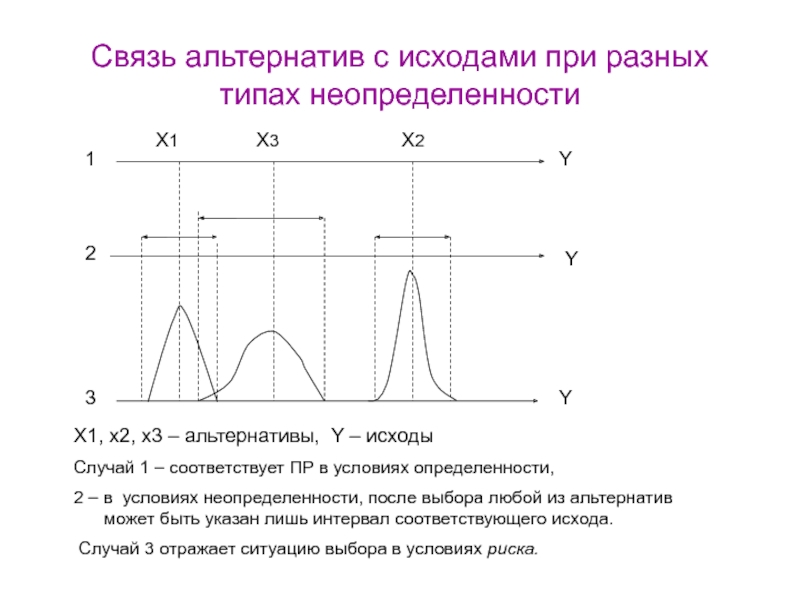
заключенногоСлайд 28Связь альтернатив с исходами при разных типах неопределенности
1
2
3
Y
Y
Y
X1
X3
X2
X1, x2, x3 – альтернативы, Y – исходы
Случай 1 –
соответствует ПР в условиях определенности, 2 – в условиях неопределенности, после выбора любой из альтернатив может быть указан лишь интервал соответствующего исхода.
Случай 3 отражает ситуацию выбора в условиях риска.
Слайд 29Пример
Во многих случаях лицо ПР, может указать лишь множество всех
тех пар исходов, для которых первый исход в паре предпочтительнее
второго.Молодой ученый выбирает место своей будущей работы, исходя из следующего множества альтернатив:
x1 – ассистент в очень престижном университете с окладом 250у.е.
X2 – доцент в электротехническом институте с окладом 350 у.е.
X3 – профессор в периферийном институте с окладом 4540 у.е.
Может быть ситуация Х1>X2, но может быть и Х2>X3, но сравнивая оклады может быть и так X3>X1
Система предпочтений задается множеством пар
(Х1,Х2), (Х2,Х3), (Х3,Х1)
Слайд 30Задачи группового выбора решений
Например. Заседание военного совета.
Пусть X={x1, x2, …
, xm} – множество вариантов решения
Имеется группа из N членов,
принимающих (выбирающих) решение.Выбор с помощью бинарных отношений
Требуется по заданной системе Ri, …, Rn индивидуальных предпочтений построить групповую (коллективную) систему предпочтений
Известен парадокс голосования
Принятие законопроекта в парламенте. Пусть три парламентские группы, обсуждают три варианта законопроекта a, b, c с целью утвердить один наилучший вариант.
Пусть система предпочтений групп имеют соответственно следующий вид:
a>b>c R1={(a,b), (b,c), (a,c)}
b>c>a R2={(b,c), (c,a), (b,a)}
с>a>b R3={(c,a), (a,b), (c,b)}
Получим a>b>c>a
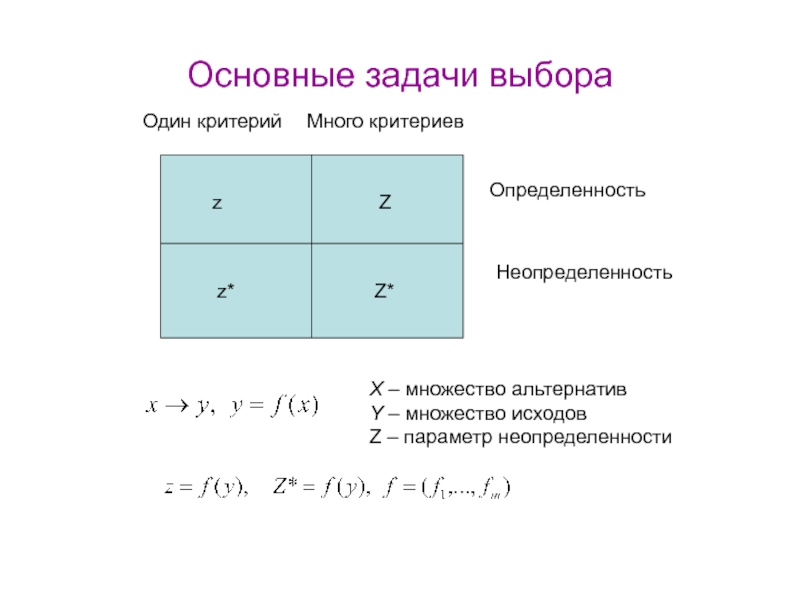
Слайд 32Основные задачи выбора
Один критерий
Много критериев
z
Z
Определенность
Неопределенность
z*
Z*
X –
множество альтернатив
Y – множество исходов
Z – параметр неопределенности
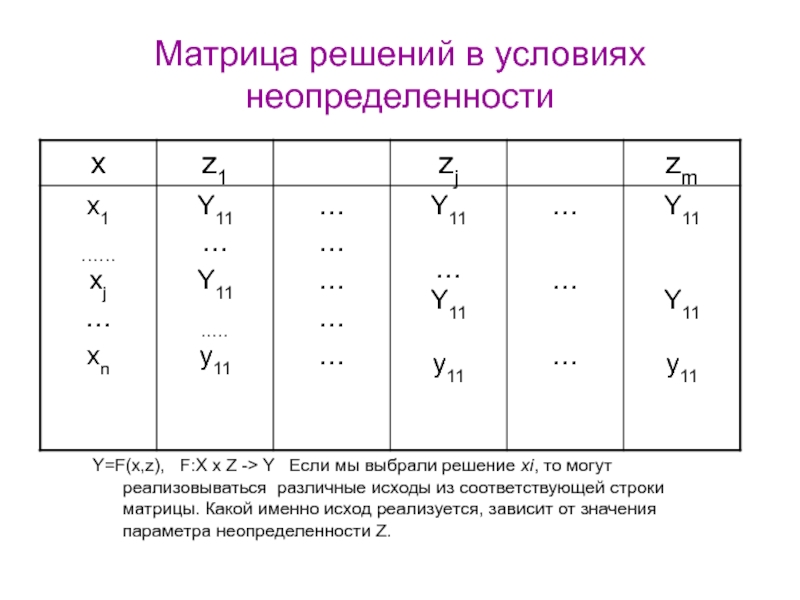
Слайд 33Матрица решений в условиях неопределенности
Y=F(x,z), F:X x Z ->
Y Если мы выбрали решение xi, то могут реализовываться
различные исходы из соответствующей строки матрицы. Какой именно исход реализуется, зависит от значения параметра неопределенности Z.Слайд 34
Критерий Лапласа опирается на принцип, что поскольку распределение вероятностей состояний
p(sj) неизвестно, то удобнее предположить , что вероятности всех состояний
природы равны между собой, т.е. p(sj)=1/n.Тогда решение максимизации успеха составит
В случае необходимости получения минимального значения ‘max’ заменяется на “min”.
Для решения задач в условиях полной неопределенности используются следующие критерии:
Критерий Лапласа,
Минимаксный критерий Вальда,
Критерий Сэвиджа,
Критерий Гурвица.
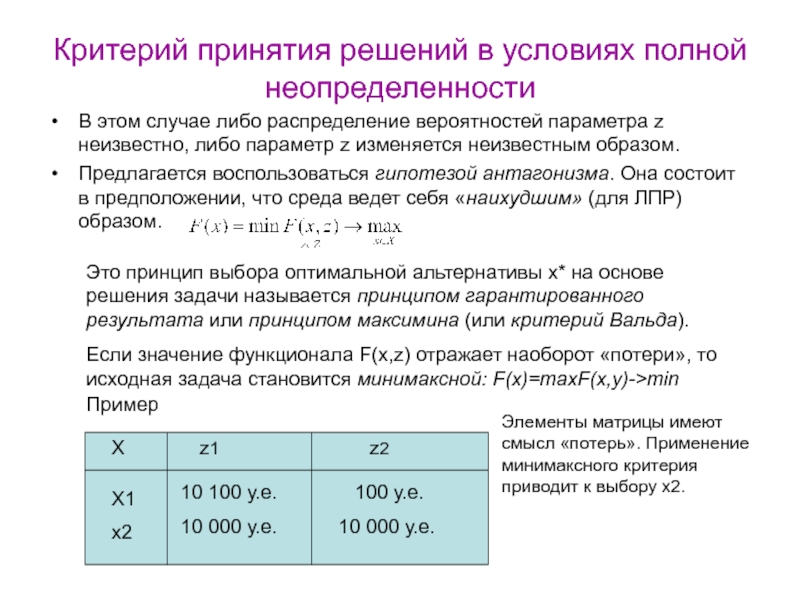
Слайд 35Критерий принятия решений в условиях полной неопределенности
В этом случае либо
распределение вероятностей параметра z неизвестно, либо параметр z изменяется неизвестным
образом.Предлагается воспользоваться гипотезой антагонизма. Она состоит в предположении, что среда ведет себя «наихудшим» (для ЛПР) образом.
Это принцип выбора оптимальной альтернативы х* на основе решения задачи называется принципом гарантированного результата или принципом максимина (или критерий Вальда).
Если значение функционала F(x,z) отражает наоборот «потери», то исходная задача становится минимаксной: F(x)=maxF(x,y)->min
Пример
X
X1
x2
z1
z2
10 100 у.е.
10 000 у.е.
100 у.е.
10 000 у.е.
Элементы матрицы имеют смысл «потерь». Применение минимаксного критерия приводит к выбору х2.
Слайд 36далее
Критерий минимального сожаления, предложенный Сэвиджем, состоит в применении минимаксного критерия
(независимо что это «доходы» или «потери»):
Матрица сожалений
X
z1
Z2
X1X2
100
0
0
9900
Согласно критерию Сэвиджа, выбираем первую альтернативу x1
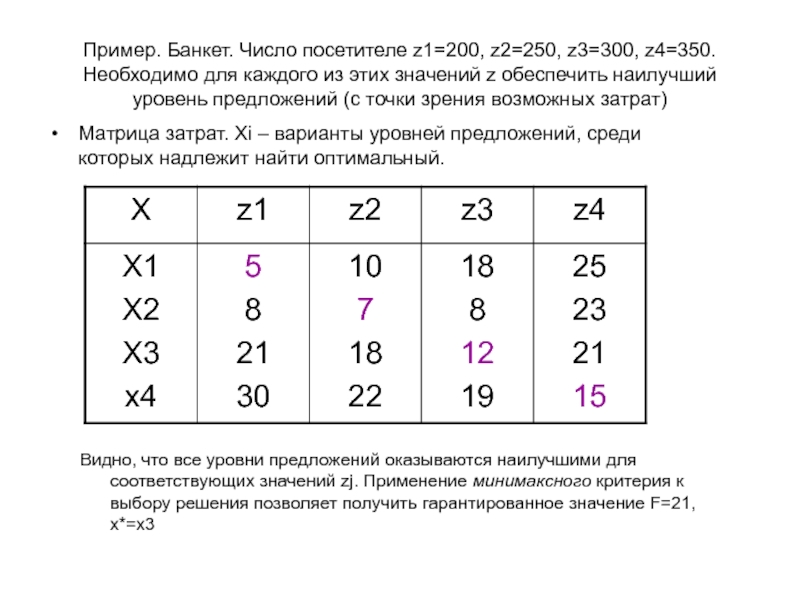
Слайд 37Пример. Банкет. Число посетителе z1=200, z2=250, z3=300, z4=350. Необходимо для каждого
из этих значений z обеспечить наилучший уровень предложений (с точки
зрения возможных затрат)Матрица затрат. Xi – варианты уровней предложений, среди которых надлежит найти оптимальный.
Видно, что все уровни предложений оказываются наилучшими для соответствующих значений zj. Применение минимаксного критерия к выбору решения позволяет получить гарантированное значение F=21, x*=x3
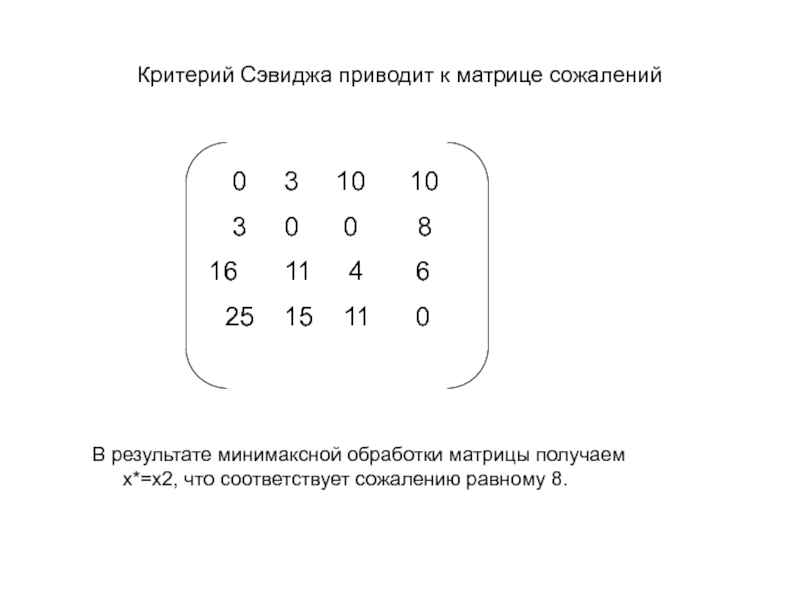
Слайд 38Критерий Сэвиджа приводит к матрице сожалений
0 3
10 10
3 0
0 811 4 6
25 15 11 0
В результате минимаксной обработки матрицы получаем х*=х2, что соответствует сожалению равному 8.
Слайд 39Критерий Гурвица
Критерий охватывает ряд различных подходов к ПР – от
наиболее оптимистичного до наиболее пессимистического
Наиболее оптимистичный подход (в предположении, что
yij означает «выигрыш» или «доход») состоит в выборе х* из условияАналогично при наиболее пессимистичных предположениях выбираемое решение соответствует max min yij
Критерий Гурвица, называемый также критерием пессимизма-оптимизма, сводится к взвешенной комбинации обоих способов, устанавливая баланс между случаями предельного оптимизма и крайнего пессимизма.
Если yij означает «прибыль», то выбирается решение из условия
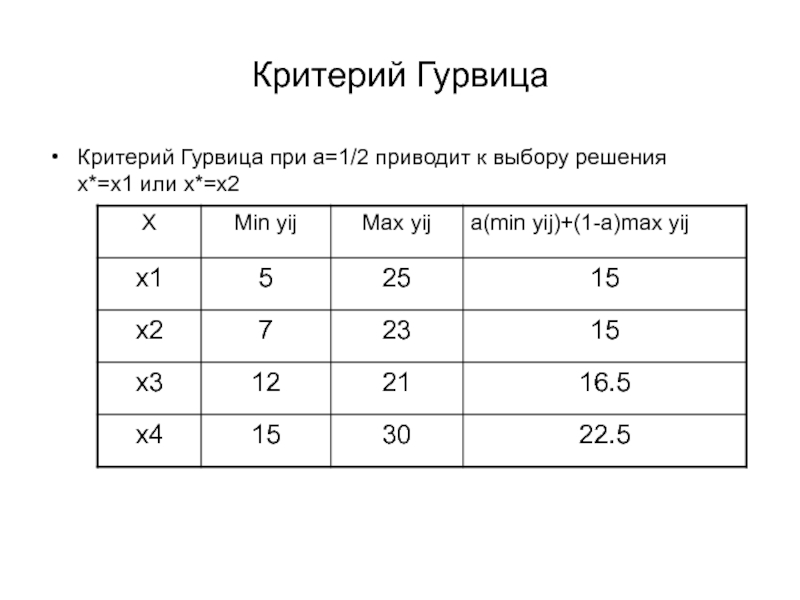
Слайд 40Критерий Гурвица
В том случае, когда yij представляет «затраты», оптимальное решение
будет соответствовать выражению
При a=1 имеем случай предельного оптимизма, при а=0
– случай крайнего пессимизма. Промежуточные значения характеризуют ту или иную склонность лица, принимающего решение, к пессимизму или оптимизму. При отсутствии выраженной склонности а=1/2.Слайд 42Экспертные системы принятия решений
Назначение и области применения ЭС
Проектирование заказных интегральных
схем
Разработка больших программных проектов
Военные приложения
Здравоохранение
Риэлтерская деятельность
Финансовый рынок и рынок ценных
бумагПринятие решений в кризисных ситуациях
Автоматизированное комплексирование заказных компьютерных систем
Информационные образовательные технологии
Системы контроля знаний обучающих
Задачи планирования и рационального распределения ресурсов и т.д.
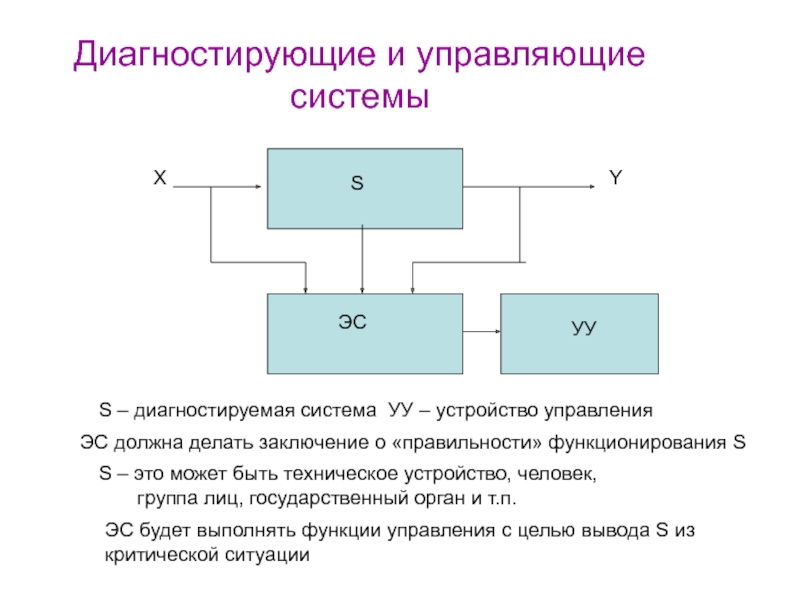
Слайд 43Диагностирующие и управляющие системы
S
ЭС
УУ
Х
Y
S – диагностируемая система УУ
– устройство управления
ЭС должна делать заключение о «правильности» функционирования S
S
– это может быть техническое устройство, человек, группа лиц, государственный орган и т.п.
ЭС будет выполнять функции управления с целью вывода S из критической ситуации
Слайд 44Классы ЭС
Диагностирующие системы
Прогнозирующие системы
Планирующие системы
Интерпретирующие (анализирующие) системы
Слайд 45Принятие решений в условиях риска
(задача о замене вратаря)
Y1(В)
x1
x2
1/6
1/2
Y2(Н)
Y3(П)
7/8
1/3
1/8
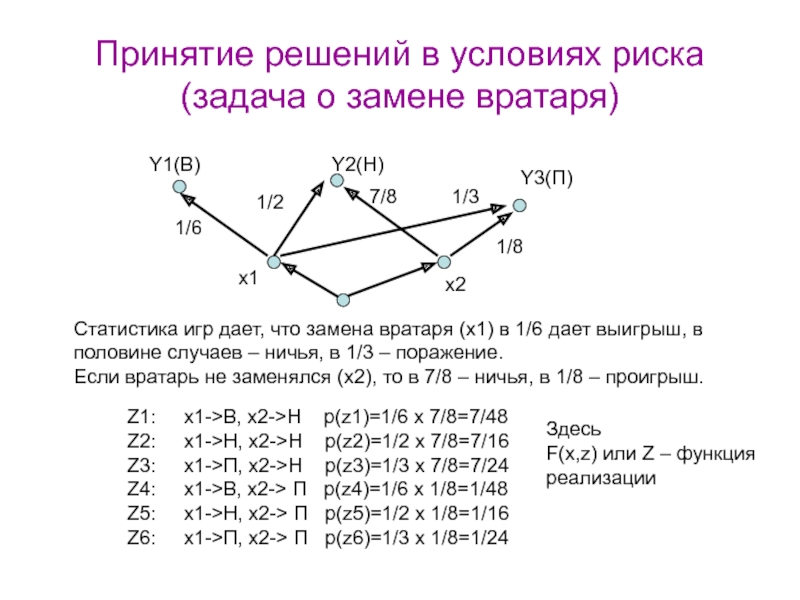
Статистика игр дает,
что замена вратаря (x1) в 1/6 дает выигрыш, в половине
случаев – ничья, в 1/3 – поражение.Если вратарь не заменялся (x2), то в 7/8 – ничья, в 1/8 – проигрыш.
Z1: x1->B, x2->H p(z1)=1/6 x 7/8=7/48
Z2: x1->H, x2->H p(z2)=1/2 x 7/8=7/16
Z3: x1->П, x2->H p(z3)=1/3 x 7/8=7/24
Z4: x1->B, x2-> П p(z4)=1/6 x 1/8=1/48
Z5: x1->H, x2-> П p(z5)=1/2 x 1/8=1/16
Z6: x1->П, x2-> П p(z6)=1/3 x 1/8=1/24
Здесь
F(x,z) или Z – функция реализации
Слайд 46продолжение
Каждому состоянию среды zj соответствует вероятность его наступления
где
- заданная
вероятность наступления исхода yj при выборе альтернативы xi
Задача оптимизации сводится
к нахождению функционала F(x,z)->maxВместо y=f(x) имеем в условиях риска в качестве функции реализации зависимость y=F(x,z).
Здесь целевая функция задана, но задана не совсем точно – она содержит неопределенный параметр z.
Правило выбора оптимальной альтернативы на основе решения задачи оптимизации называется критерием математического ожидания (или критерием Байеса-Лапласа).
Слайд 47Далее
Будем численно оценивать исход игры по получаемым очкам:
В –
2 очка, Н – 1 очко, П – 0 очков
Получим
матрицу успехов при замене вратаряF(x1,z)=2(7/48)+1(7/16)+2(1/48)+1(1/16)=5/6=0.833
F(x2,z)=1(7/48)+1(7/16)+1(7/24)=7/8=0.875
F(x2,z)>F(x1,z) заменять вратаря нецелесообразно.
Если за победу будут давать 3 очка, тогда F(x1,z)=0,979,
замена вратаря была бы целесообразной.