Слайд 2Page
Преобразование Фурье
4.1. Ряд Фурье.
4.2.Временная и частотные области сигнала.
4.3. Комплексная
форма ряда Фурье.
4.4. Интеграл Фурье.
4.5. Преобразование Фурье.
4.6. Синус- и косинус-преобразования.
4.7.
Фурье-образ δ-функции.
4.8. Свойства преобразования Фурье.
4.9. Преобразование Фурье тригонометрических функций.
4.10. Оконные функции.
Слайд 3Page
Преобразование Фурье
4.11. Оконные функции.
4.12. Равенство Парсеваля.
4.13. Применение равенства Парсеваля.
4.14.
Энергия гармонического осциллятора.
4.15. Приложения преобразования Фурье.
4.16. Таблица преобразований Фурье.
Слайд 4Page
4.1. Ряд Фурье
Ряд Фурье и преобразование Фурье – основные
инструменты гармонического анализа.
Вначале рассмотрим разложение в ряд Фурье функции x(t)
Слайд 5Page
Ряд Фурье
В основе ряда Фурье лежат тригонометрические ортогональные функции.
Величина T является периодом разложения, соответственно ω = 2π/T –
частота (угловая скорость).
Ортогональность базисных функций разложения
по определению означает, что
Легко проверить ортогональность базисных функций Фурье интегрированием.
Слайд 6Page
Ряд Фурье
Например,
Упражнение. Проверить ортогональность функций cos(mωt) и cos(nωt) 1)
для m=n; 2) для m≠n.
Слайд 7Page
Ряд Фурье
Коэффициенты Ak, Bk ряда Фурье вычисляются с применением
свойства ортогональности базисных функций.
Коэффициенты Ak, Bk равны:
Слайд 8Page
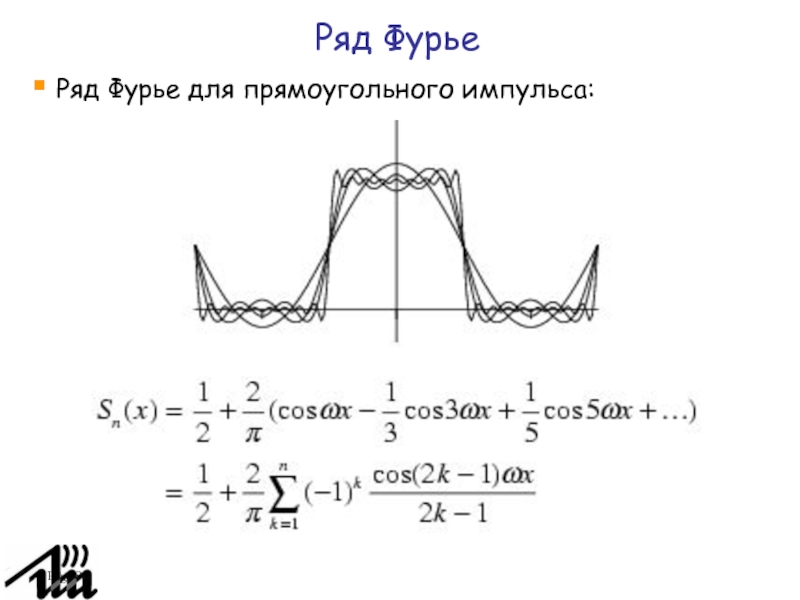
Ряд Фурье
Ряд Фурье для прямоугольного импульса:
Слайд 9Page
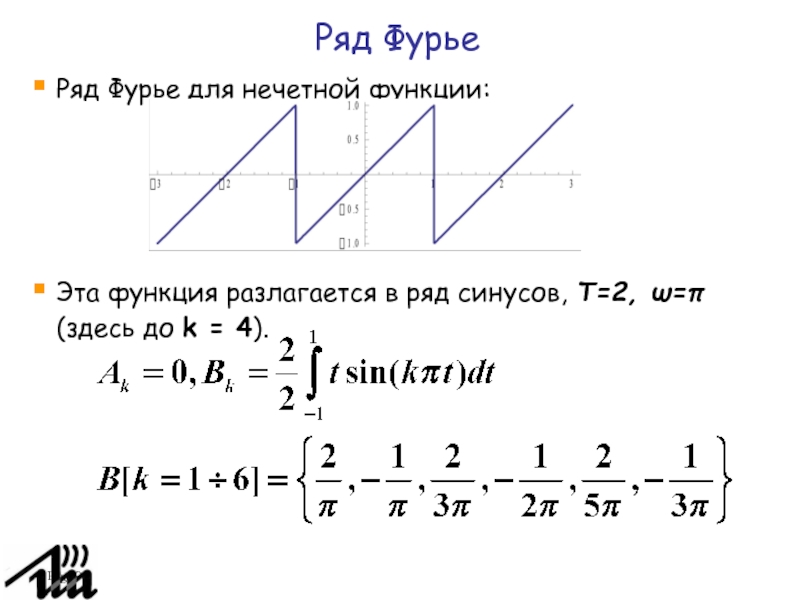
Ряд Фурье
Ряд Фурье для нечетной функции:
Эта функция разлагается в
ряд синусов, T=2, ω=π (здесь до k = 4).
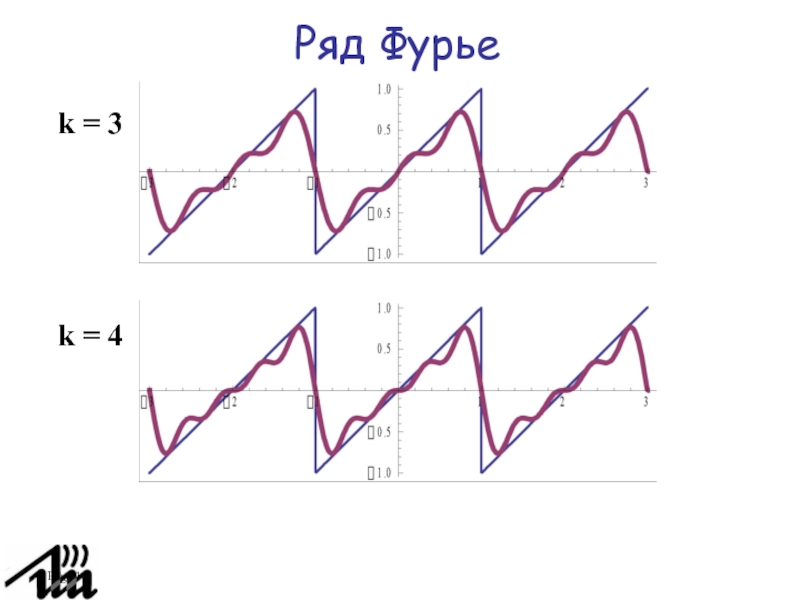
Слайд 12Page
Ряд Фурье
Ряд Фурье разложения нечетной функции не содержат базисных
функций cos(·).
При разложения четной функции ряд Фурье не содержат
базисных функций sin(·).
Разложим x(t) = t2 на отрезке [-1, 1], то есть T=2. Функция четная, поэтому ряд содержит только cos(·).
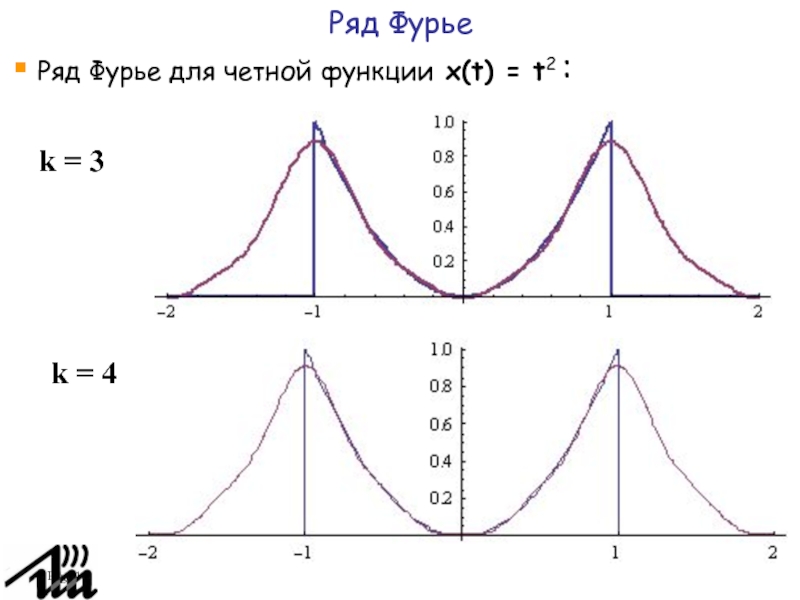
Слайд 13Page
Ряд Фурье
Ряд Фурье для четной функции x(t) = t2
(Т=2) :
k = 1
k = 0
k = 2
Слайд 14Page
Ряд Фурье
Ряд Фурье для четной функции x(t) = t2
:
k = 3
k = 4
Слайд 15Page
Ряд Фурье
Следует заметить, что ряд Фурье для некоторых функций
расходится, в этом случае говорят, что функция не разлагается в
ряд Фурье.
[Аналогично, для некоторых функций не существует преобразования Лапласа - соответствующий интеграл расходится].
Слайд 16Page
Сигнал моделируется в виде функции x(t), зависящей от времени
t. Говорят, что сигнал моделируется во временной области. При разложении
в ряд Фурье с периодом T сигнал представляется в виде ряда от sin(·) и cos(·) от аргументов ω, 2ω, 3ω, . . ., где частота
ω = 2π/T.
Таким образом, сигнал разлагается по функциям с аргументами, содержащими частоты kω. Коэффициенты Ак и Вк называются частотными коэффициентами. Такое представление сигнала называется представлением в частотной области.
Из представления x(t) во временной области разложением в ряд Фурье можно получить представление в частотной области и наоборот (но обратное представление из ряда Фурье в функцию x(t) неоднозначно).
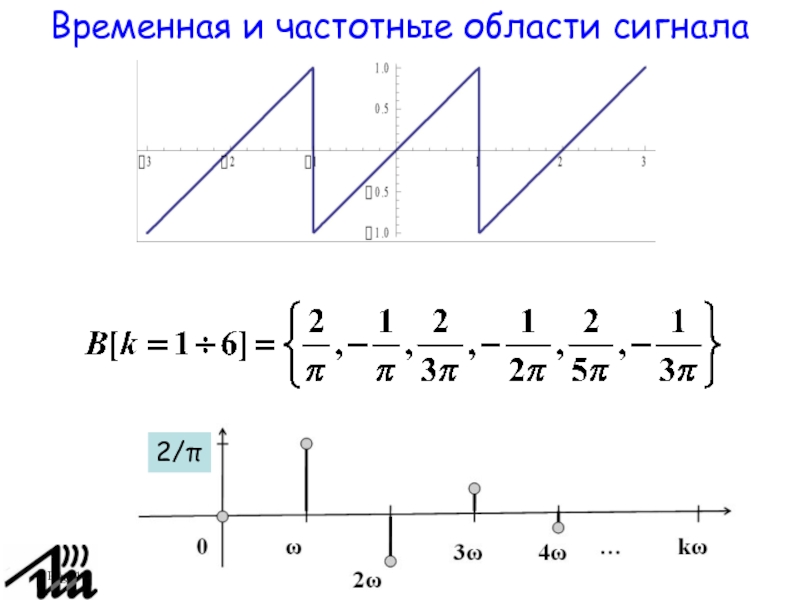
4.2.Временная и частотные области сигнала
Слайд 17Page
Временная и частотные области сигнала
2/π
Слайд 18Page
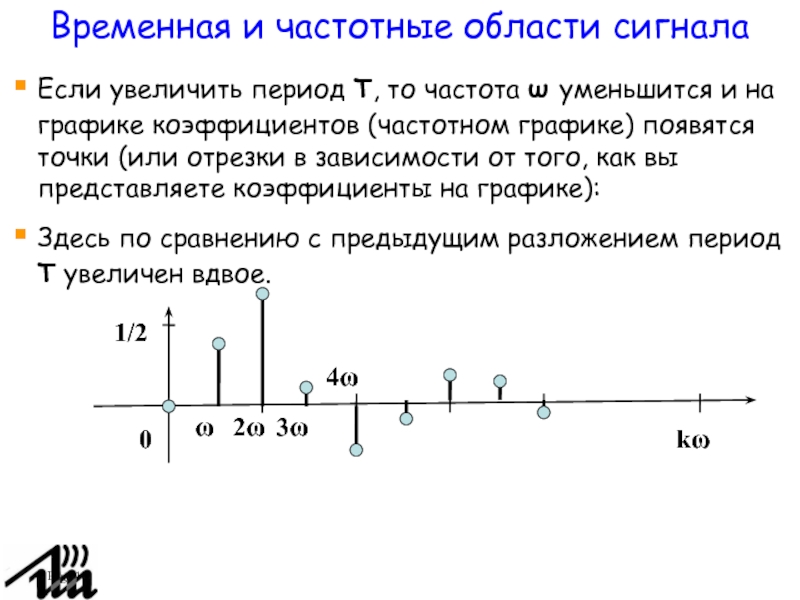
Если увеличить период T, то частота ω уменьшится и
на графике коэффициентов (частотном графике) появятся точки (или отрезки в
зависимости от того, как вы представляете коэффициенты на графике):
Здесь по сравнению с предыдущим разложением период T увеличен вдвое.
0
1/2
ω
2ω
3ω
4ω
kω
Временная и частотные области сигнала
Слайд 19Page
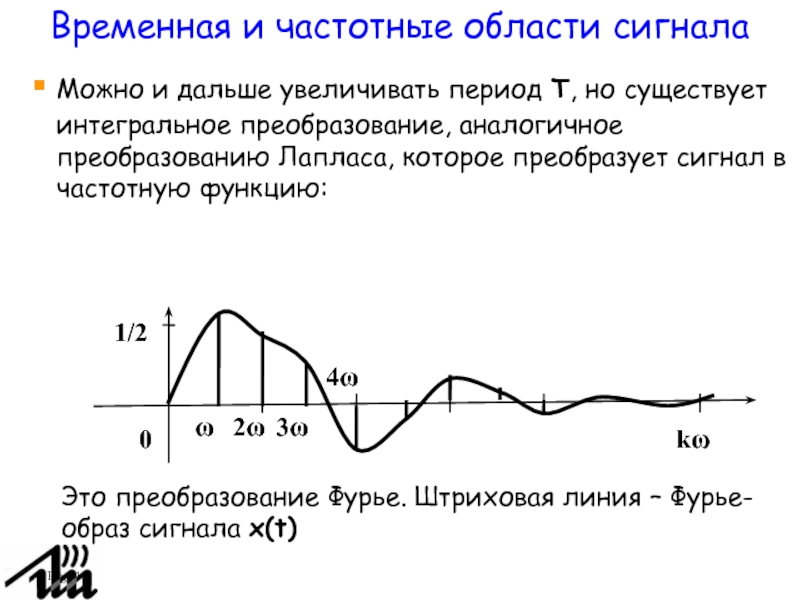
Можно и дальше увеличивать период T, но существует интегральное
преобразование, аналогичное преобразованию Лапласа, которое преобразует сигнал в частотную функцию:
0
1/2
ω
2ω
3ω
4ω
kω
Это
преобразование Фурье. Штриховая линия – Фурье-образ сигнала x(t)
Временная и частотные области сигнала
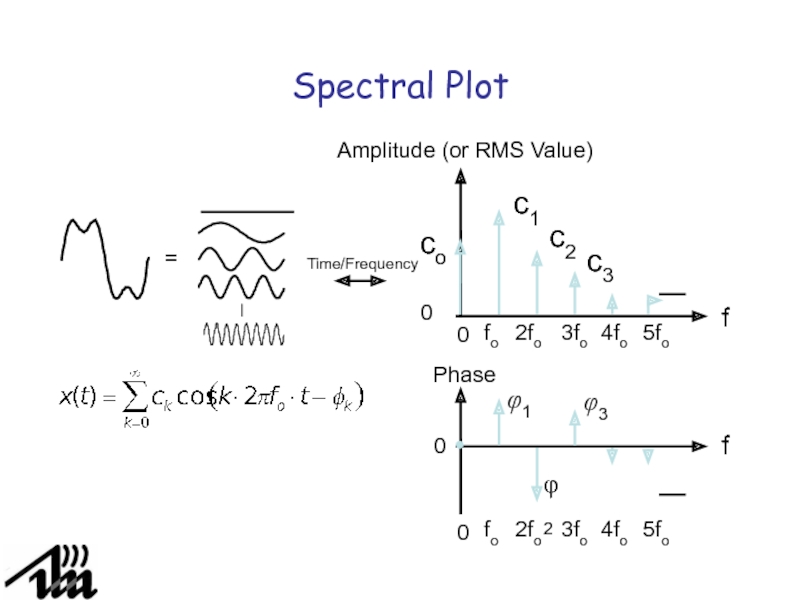
Слайд 20Spectral Plot
=
Phase
f
fo
2fo
3fo
4fo
5fo
0
0
φ1
φ2
φ3
Слайд 21Page
Известна формула Эйлера, связывающая экспоненту с тригонометрическими функциями.
4.3. Комплексная
форма ряда Фурье
Ряд Фурье принимает вид
Слайд 22Page
Введем новые обозначения
где Ck и C-k комплексные числа. Запишем
ряд Фурье в комплексной форме:
4.3. Комплексная форма ряда Фурье
Ck и
C-k комплексно сопряженные числа. Зная один из коэффициентов Ck или C-k, можно найти другой, поменяв знак мнимой части. Это означает, что в комплексной форме достаточно разложить сигнал x(t) только для k = 0, 1, 2, … или для k = 0, -1, -2, … и изменив знак мнимой части, получить остальные коэффициенты.
Слайд 23Page
Вещественные числа
называются спектром амплитуд сигнала.
4.3. Комплексная
форма ряда Фурье
- спектр фаз
- спектр мощности (или энергии) сигнала
(подробнее рассмотрим при изучении равенства Парсеваля).
Слайд 24Page
4.4. Интеграл Фурье
Разложение в ряд Фурье предполагает знание периода
T = 2π/ω разложения. Ряд Фурье в комплексной экспоненциальной форме
содержит амплитуды частот сигнала.
Преобразование Фурье (рассмотрим позже) не зависит от периода T и вместо последовательности амплитуд частот строит функцию амплитуд (плотность спектра).
Представим ряд Фурье в виде интеграла, это и будет интеграл Фурье.
Ряд Фурье имеет вид :
Слайд 25Page
Коэффициенты подставим в ряд
4.4. Интеграл Фурье
Функции
не зависят от переменной интегрирования u, как постоянные величины их можно внести под знак интеграла. По формуле
преобразуем подынтегральное выражение :
Слайд 26Page
4.4. Интеграл Фурье
Положим
Тогда сигнал x(t) разлагается в ряд:
и сумма
стремится к интегралу по z, при этом если в первом слагаемом интеграл
сходится, то первое слагаемое ряда стремится к нулю.
В пределе
4.4. Интеграл Фурье
Слайд 28Page
Ввиду четности cos(·) изменим предел интегрирования и в результате
окончательно получаем интеграл Фурье:
4.4. Интеграл Фурье
Вместе с интегралом Фурье рассмотрим
функцию
Если этот интеграл существует, то g(z) – нечетная функция по z. Если интегрировать эту функцию на интервале [A, -A]
Слайд 29Page
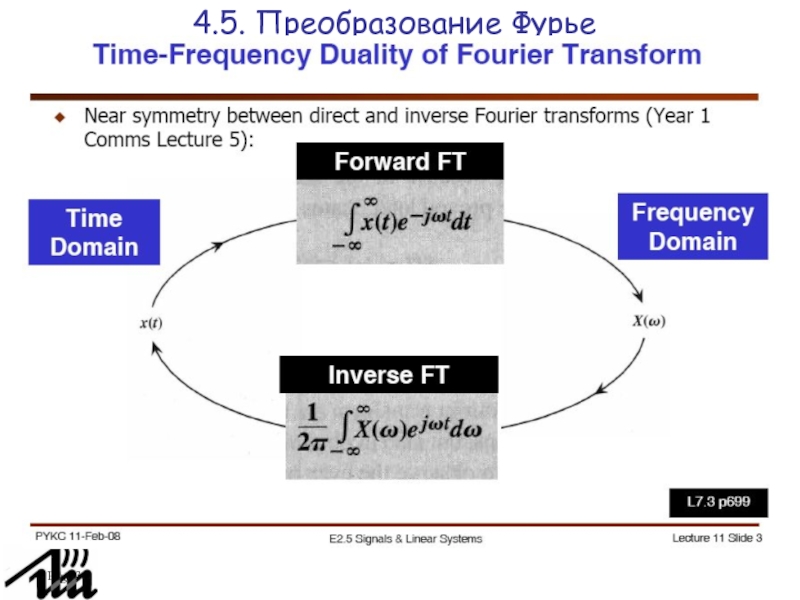
4.5. Преобразование Фурье
Умножим интеграл от sin(·) на i/2π
И сложим
с интегралом Фурье
Теперь после внесения под общий знак интеграла и
применения формулы Эйлера :
Слайд 30Page
4.5. Преобразование Фурье
или
Интегральное преобразование
Называется прямым преобразованием Фурье
Слайд 31Page
4.5. Преобразование Фурье
Интегральное преобразование
Называется обратным преобразованием Фурье.
Функция X(z) называется
Фурье-образом функции x(t), а функция x(t) называется Фурье-прообразом функции X(z).
По
аналогии со спектром амплитуд |X(z)|, называется амплитудной функцией, а Arg(X(z)) фазовой функцией для X(z).
Слайд 32Page
4.5. Преобразование Фурье
Из формулы вывода преобразования имеем
Мы получаем, что
Если
переставить в формуле интегралы, то
Слайд 33Page
4.5. Преобразование Фурье
При выводе формулы преобразования предполагалось, что переменная
t – вещественная, но подынтегральное выражение преобразования – функция комплексной
переменной, так как содержит мнимую единицу i
То есть вещественная функция вещественной переменной преобразуется в комплексную функцию от вещественной переменной.
В общем случае можно считать, что и t и z – комплексные переменные. Тогда преобразования Фурье – это преобразования на комплексной плоскости.
Слайд 35Page
4.6. Синус- и косинус-преобразования
Однако для некоторых вещественных функций x(t)
их Фурье-образ X(z) – тоже вещественная функция. При выводе преобразования
Фурье применялся интеграл Фурье
Представим cos z(t-u) как косинус суммы и получим
Второй интеграл по dz равен нулю как интеграл по симметричному отрезку от нечетной функции, поэтому
Слайд 36Page
4.6. Синус- и косинус-преобразования
Они называются соответственно прямым и обратным
косинус-преобразованием. Косинус-преобразования переводят вещественную функцию в вещественную.
Слайд 37Page
Аналогично из формулы
4.6. Синус- и косинус-преобразования
Вопрос. Почему формулы косинус-преобразований
содержат множитель ?
получаем прямое и
обратное синус-преобразование
Слайд 38Page
Синус-преобразования переводят вещественную функцию в вещественную.
Преобразование Фурье произвольной функции
x(t) можно представить как сумму ее косинус и синус-преобразований:
4.6. Синус-
и косинус-преобразования
Если функция x(t) четная, то ее преобразование Фурье равно косинус-преобразованию ( синус-преобразование такой функции равно нулю).
Если функция x(t) нечетная, то ее преобразование Фурье равно синус-преобразованию, умноженному на мнимую единицу ( косинус-преобразование равно нулю).
Слайд 39Page
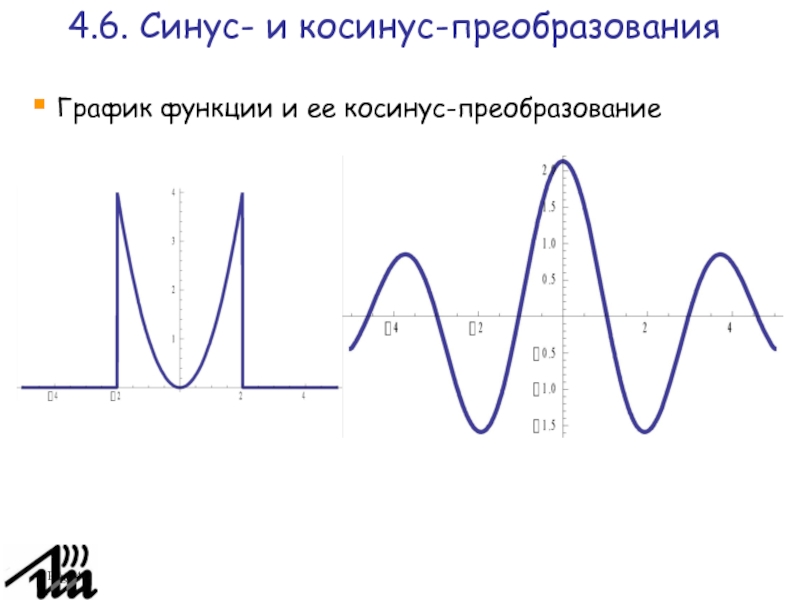
Пример. Найти преобразование Фурье функции
Функция четная, поэтому ее преобразование
Фурье сводится к косинус-преобразованию.
4.6. Синус- и косинус-преобразования
Слайд 40Page
График функции и ее косинус-преобразование
4.6. Синус- и косинус-преобразования
Слайд 41Page
Пример. Найти преобразование Фурье функции
Функция четная, ее преобразование Фурье
сводится к косинус-преобразованию.
4.7. Фурье-образ δ-функции
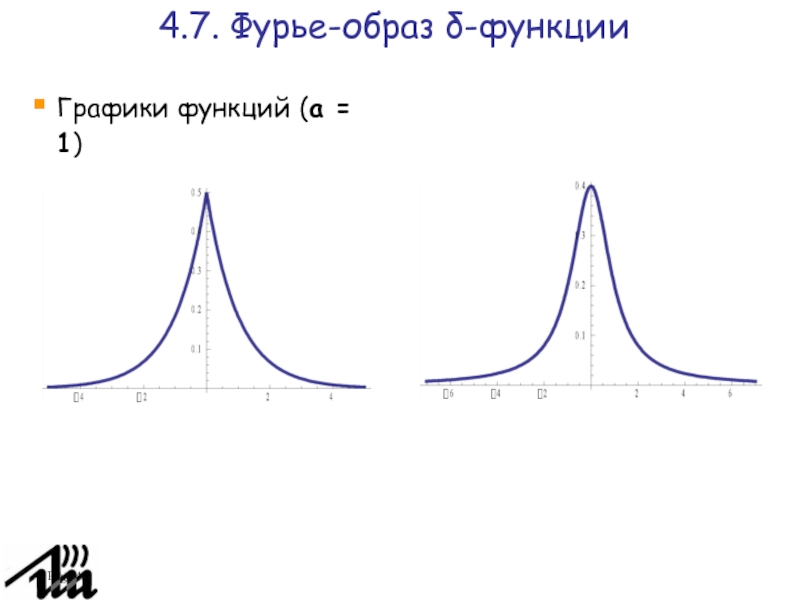
Слайд 42Page
Графики функций (а = 1)
4.7. Фурье-образ δ-функции
Слайд 43Page
Интеграл от функций
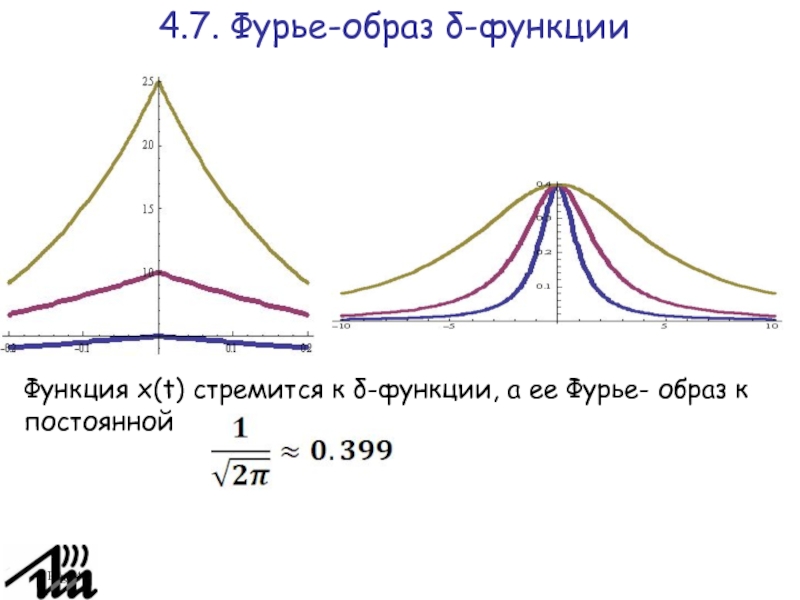
Функция x(t) стремится к δ-функции, а
ее Фурье – образ к постоянной
- (для
этого подобран множитель a/2 ).
При функция то есть в пределе получаем δ-функцию.
4.7. Фурье-образ δ-функции
Слайд 44Page
Функция x(t) стремится к δ-функции, а ее Фурье- образ
к постоянной
4.7. Фурье-образ δ-функции
Слайд 45Page
При исходная
функция стремится к δ – функции, а ее Фурье-образ к
постоянной
Доказывается, что преобразование Фурье δ–функции равно константе
Верно и то, что обратное преобразование Фурье от постоянной функции F(z) = c равно δ–функции с некоторым коэффициентом.
4.7. Фурье-образ δ-функции
Слайд 46Page
и найдем ее Фурье-образ.
Функция четная, поэтому достаточно вычислить ее
косинус-преобразование.
4.7. Фурье-образ δ-функции
Определим прямоугольную функцию
Слайд 47Page
Функция
4.7. Фурье-образ δ-функции
Часто встречается в физических приложениях, она
получила специальное обозначение sinc t.
График этой функции
Слайд 48Page
4.7. Фурье-образ δ-функции
Можно выразить Фурье-образ прямоугольной функции через функцию
sinc t.
Слайд 49Page
4.7. Фурье-образ δ-функции
Для a=1/ε получаем прямоугольный импульс, найдем его
Фурье-образ :
Если ε → 0, то эта функция стремится
к
То есть снова получено, что преобразование Фурье δ-функции равно
Слайд 50Page
Свойства преобразование Фурье похожи на свойства преобразования Лапласа :
1.
Линейность F(a·f(t) + b·g(t)) = a·F(f(t)) + b·F(g(t)).
2. Свойство
сдвига
3. Преобразование производной
4.8. Свойства преобразования Фурье
4. Преобразование интеграла
Слайд 51Page
Свойства 1 и 2 доказываются совершенно аналогично соответствующим свойствам
преобразования Лапласа :
Свойство 3 (преобразование производной) докажем применением замечательного предела
4.8.
Свойства преобразования Фурье
Слайд 52Page
Найти преобразования Фурье функции cos(t).
4.9. Преобразование Фурье тригонометрических функций
Слайд 53Page
4.9. Преобразование Фурье триг. функций
При z=+1 и z=-1
имеем особые точки, нужно показать, что
Это доказывается по определению
двойного предела, затем применяется замечательный предел для sin x/x.
Слайд 54Page
4.9. Преобр Фурье триг. функций– доказывал упрощенно! (НЕ НУЖНО
для экзамена)
Слайд 55Page
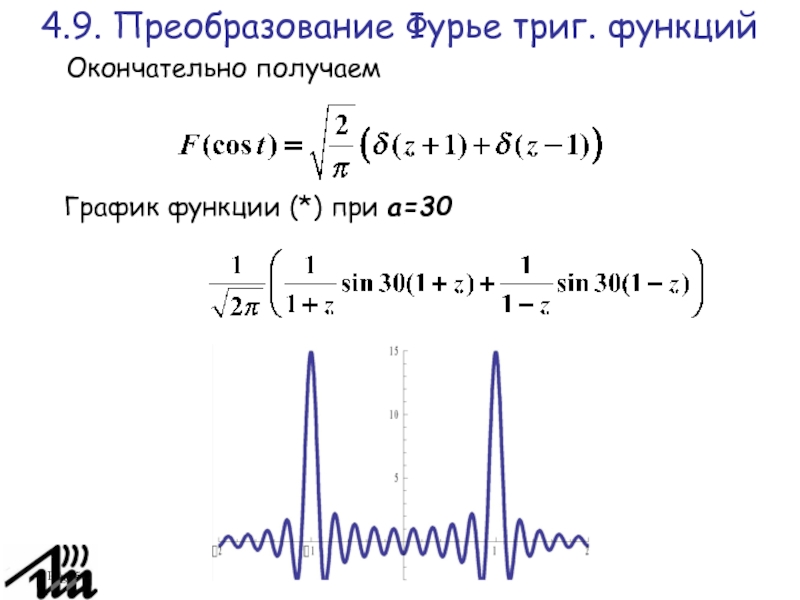
Окончательно получаем
4.9. Преобразование Фурье триг. функций
График функции (*)
при a=30
Слайд 56Page
Найти преобразования Фурье функции sin(t).
По формуле приведения
4.9. Преобразование Фурье
триг. функций
Тогда по свойству 2 (сдвиг)
По формуле Эйлера
Слайд 57Page
Найдем преобразования Фурье свертки сигналов f(t) и g(t).
4.10. Преобразование
Фурье для свертки
Слайд 58Pagе
Обратное преобразование Фурье от свертки функций
Вывод формулы основан на
свойстве сдвига
Доказательство проводится заменой переменной в интеграле :
4.10. Преобразование
Фурье для свертки
Слайд 59Page
Если к обеим частям равенства применить прямое преобразование Фурье,
то получим формулу для преобразования произведения сигналов
4.10. Преобразование Фурье для
свертки
Слайд 60Page
Исследование Фурье-образа сигнала называется спектральным анализом. Время наблюдения реального
сигнала ограничено. Для того, чтобы провести достоверный спектральный анализ сигнала,
во многих приложениях необходим бесконечный временной интервал t ϵ (-∞, + ∞). Поскольку в реальных ситуациях это невозможно, то для преобразования сигнала используются оконные функции.
В простейшем случае это просто ограничение сигнала на некотором интервале, это симметричный интервал с серединой в точке t, то есть используется прямоугольная функция
4.11. Оконные функции
Слайд 61Page
Произведение сигнала g(t) на эту функцию
4.11. Оконные функции
ограничивает
сигнал g(t) на интервале [-ε/2, ε/2]
Слайд 62Page
Наблюдаемый сигнал математически равен произведению
4.11. Оконные функции
Преобразование Фурье
этого произведения
В частности, если g(t) = cos(t), то
Слайд 63Page
4.11. Оконные функции
Так как свертка δ(t) с сигналом
g(t) равна
Слайд 64Page
4.11. Оконные функции
то
окончательно
Сравните с
Слайд 65Page
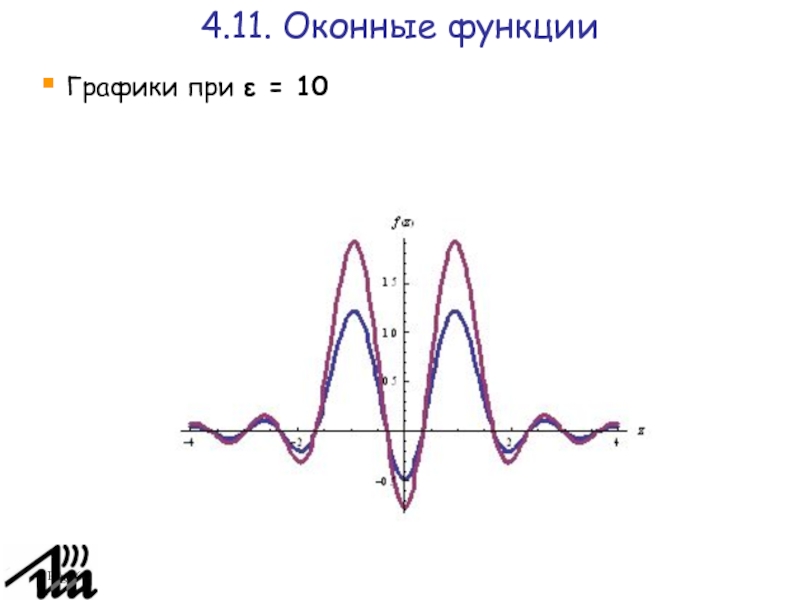
4.11. Оконные функции
Графики при ε = 10
Слайд 66Page
4.11. Оконные функции
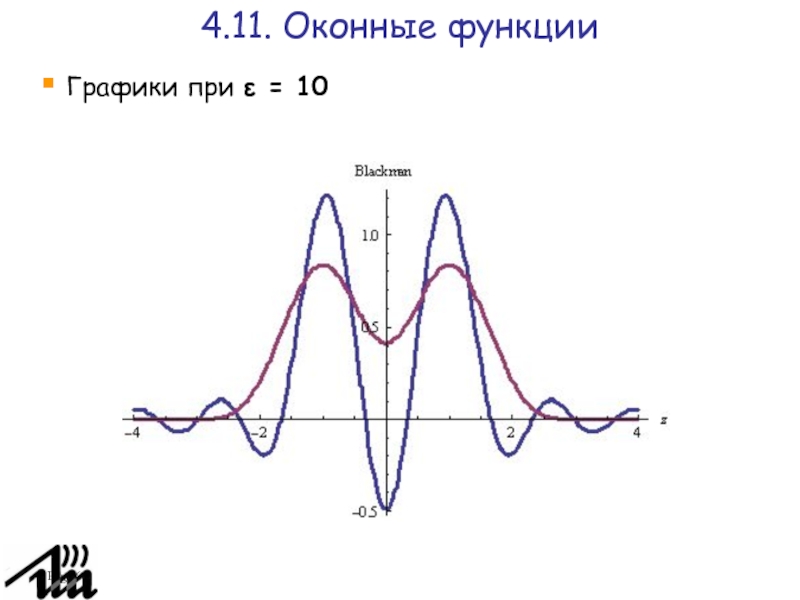
Для разных целей и разных сигналов
могут использоваться различные оконные функции. Так, при применении оконной функции
Блэкмана
получаем
- сложное аналитическое выражение, которое ближе к Фурье-образу сигнала cos(t), чем свертка с прямоугольной функцией.
Слайд 67Page
4.11. Оконные функции
Графики при ε = 10
Слайд 68Example 2.3.14 (2/2) Пример слайда по этой теме из другого
университета
Figure 2.38 Effect of modulation in both the time and
frequency domain.
Слайд 69Page
4.12. Равенство Парсеваля
Равенство Парсеваля (теорема Планшереля) – один
из основных инструментов, составляющих методы анализ сигнала. Позволяет оценить энергию
сигнала во временном и частотном представлении.
Энергия сигнала (мощность, работа, которую сигнал может совершить).
Пусть сигнал во временном представлении выражает зависимость напряжения от времени x(t).
Если ток, генерирующий сигнал, проходит по проводнику с сопротивлением R, то сила тока i(t) = x(t)/R, и тогда мощность электрического тока
w(t) = x(t)· i(t) = x(t)2/R.
Слайд 70Page
Следовательно, мощность сигнала
пропорциональна величине x(t)2 , а если R=1,
то равна этой величине. Тогда, по определению, работа, которую совершает
электрический ток, или которую он может совершить (энергия), пропорциональна (в исключительных случаях равна)
4.12. Равенство Парсеваля
Слайд 71Page
В общем случае, когда x(t) – комплексное выражение,
где
- комплексное сопряженное к
Преобразование Фурье позволяет
установить соответствие между энергией сигнала во временной и частотной областях.
4.12. Равенство Парсеваля
Слайд 72Page
Будем предполагать, что x(t) - вещественная функция от вещественной
переменной t, а ее Фурье–образ X(z) – комплексная функция от
вещественной переменной z.
При существовании интегралов для правой части верно соотношение
4.12. Равенство Парсеваля
Докажем равенство Парсеваля
Слайд 73Page
Представим квадрат модуля в удобном виде
4.12. Равенство Парсеваля
Запишем
Фурье-образы в последнем интеграле
Слайд 74Page
для комплексной функции X(z) от вещественного аргумента z
4.12.
Равенство Парсеваля
потому что в выражении через косинус- и синус-
преобразования
Слайд 75Page
Найдем Фурье-прообраз этой функции
4.12. Равенство Парсеваля
после замены w
= -z
Слайд 76Page
То есть
4.12. Равенство Парсеваля
Следовательно,
заменим переменную в последнем
интеграле
Слайд 77Page
вернемся к прямоугольному импульсу
4.12. Равенство Парсеваля
и изменим порядок
интегрирования
Выражение в скобках – это преобразование Фурье прямоугольного импульса
Слайд 78Page
Теперь внутренний интеграл (по переменной μ) является сверткой
4.12. Равенство Парсеваля
Перейдем к пределу
Слайд 79Page
После этого во внутреннем интеграле получаем свертку:
По свойству свертки
с импульсом
4.12. Равенство Парсеваля
Окончательно получили:
Слайд 80Page
4.13. Применение равенства Парсеваля
Пример. Найти энергию сигнала
где
параметр a>0.
Энергия, вычисленная во временной области,
в частотной области
Слайд 81Page
Тогда энергия, вычисленная в частотной области
4.13. Применение равенства
Парсеваля
То есть, действительно, энергия, вычисленная в частотной области совпадает
с энергией вычисленной во временной области
Слайд 82Page
Пример. Найти диапазон частот W=[-w, +w] такой, что 95%
энергии сигнала
излучается частотами этого диапазона.
Энергия в частотной области излучаемая частотами диапазона [-w, +w] равна
4.13. Применение равенства Парсеваля
Слайд 83Page
По предыдущему примеру
4.13. Применение равенства Парсеваля
Энергия, излучаемая
всем допустимом диапазоне частот, равна 1/2a. Составляем уравнение и находим
w (в радианах).
Перейдем к измерению частоты в Hz.Пусть a=1, 2π радиан – это 1 оборот, то есть
95% энергии сигнала потребляют (рассеивают) частоты диапазона от -2 Hz до 2 Hz , то есть сигнал x(t) низкочастотный.
Слайд 84Page
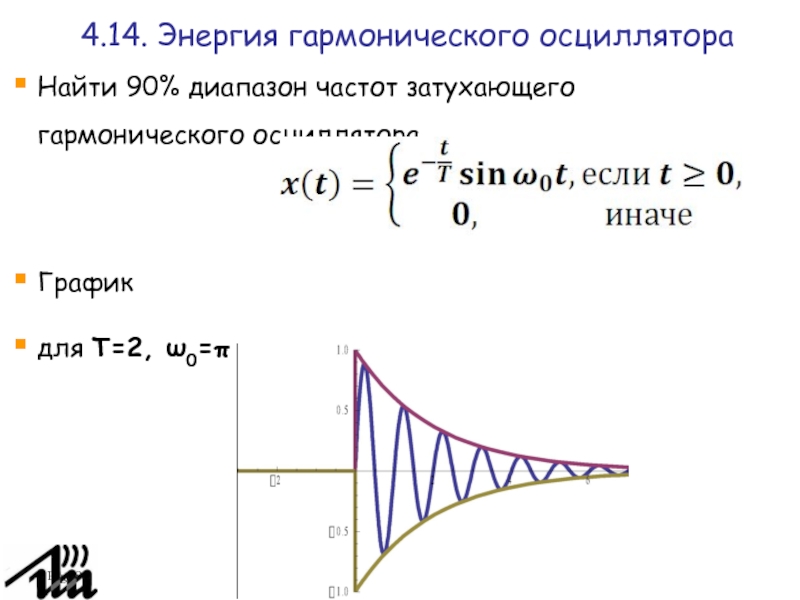
Найти 90% диапазон частот затухающего гармонического осциллятора
График
для T=2,
ω0=π
4.14. Энергия гармонического осциллятора
Слайд 85Page
Найдем Фурье-образ осциллятора и оценим его энергию. Интеграл находим
по частям, после нескольких интегральных и алгебраических преобразований получаем :
4.14. Энергия гармонического осциллятора
Слайд 86Page
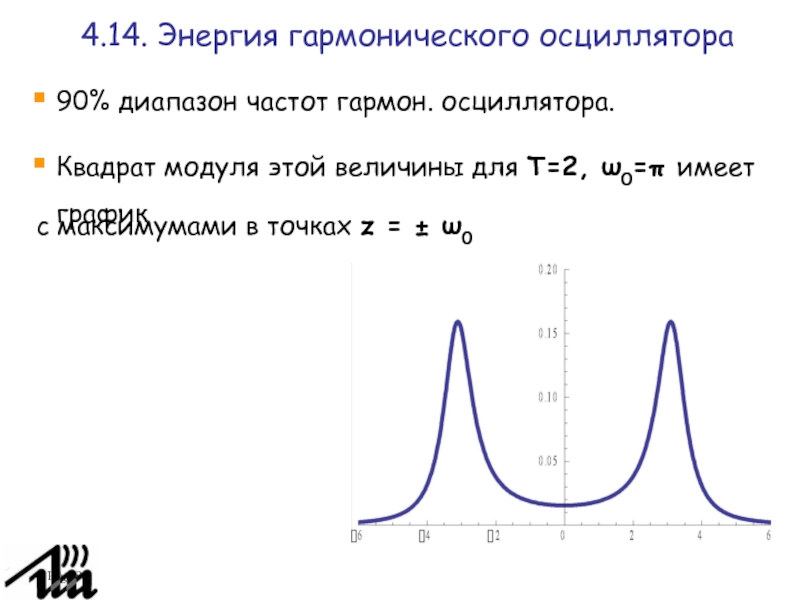
90% диапазон частот гармон. осциллятора.
Квадрат модуля этой величины для
T=2, ω0=π имеет график
c максимумами в точках z = ±
ω0
4.14. Энергия гармонического осциллятора
Слайд 87Page
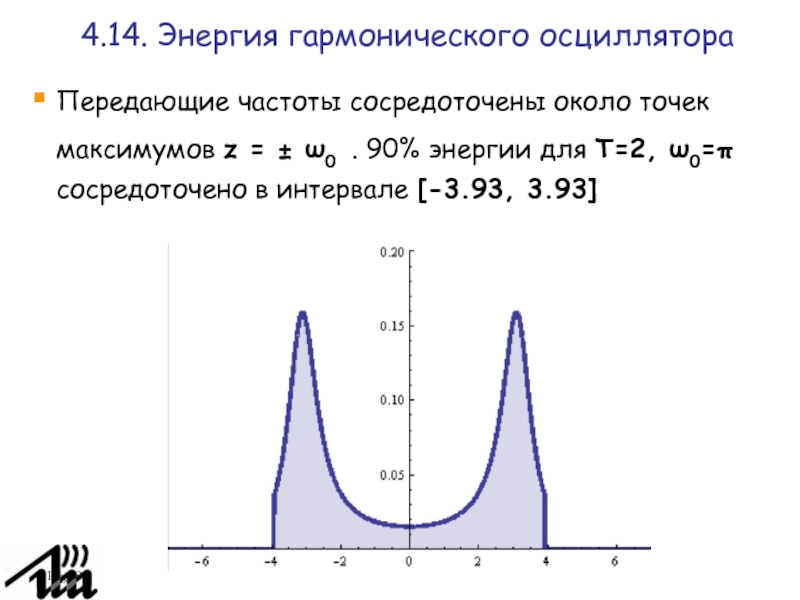
Передающие частоты сосредоточены около точек максимумов z = ±
ω0 . 90% энергии для T=2, ω0=π сосредоточено в интервале
[-3.93, 3.93]
4.14. Энергия гармонического осциллятора
Слайд 88Page
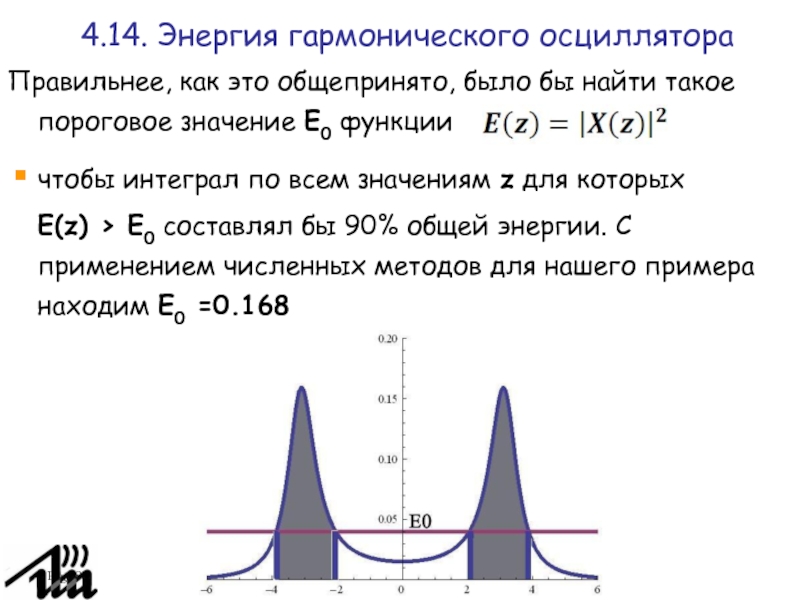
Правильнее, как это общепринято, было бы найти такое пороговое
значение E0 функции
чтобы интеграл по всем значениям z для которых
E(z) > E0 составлял бы 90% общей энергии. С применением численных методов для нашего примера находим E0 =0.168
4.14. Энергия гармонического осциллятора
Слайд 89Page
и получаем два интервала [-4.34, -0.72] и [0.72, 4.34]
(в радианах). В герцах это низкочастотный диапазон 0.110.69 Hz.
4.14.
Энергия гармонического осциллятора
Слайд 90Page
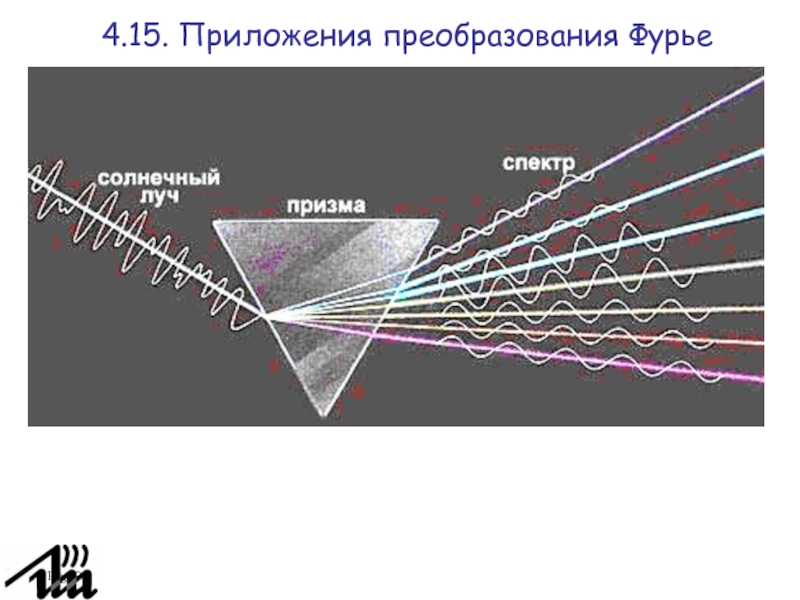
Преобразование Фурье вычисляется всякий раз, когда мы слышим звук.
Ухо автоматически выполняет вычисление, которое мы можем выполнить лишь после
нескольких лет обучения математике. Наш орган слуха представляет звук — колебательное движение частиц упругой среды, распространяющееся в виде волн в газообразной, жидкой или твёрдых средах — в виде спектра частот (низкие – высокие), каждому небольшому интервалу частот соответствует громкость – энергия на этом интервале. Мозг интерпретирует эту информацию как воспринимаемый звук.
4.15. Приложения преобразования Фурье
Слайд 91Page
Вопрос о сходимости рядов Фурье для тех или иных
классов функций привёл к появлению новых областей в математике. Одним
из примеров в этом смысле является теория обобщённых функций, в рамках этой теории была подведена теоретическая основа под такие функции, как ступенька Хевисайда и дельта-функция Дирака (последняя описывает область единичной площади, сконцентрированную в бесконечно малой окрестности точки). Благодаря этой теории преобразование Фурье стало применимым для решения уравнений, в которых фигурируют такие интуитивные понятия, как точечная масса, точечный заряд, магнитные диполи, сосредоточенная нагрузка на балке.
4.15. Приложения преобразования Фурье
Слайд 92Page
Ряды Фурье и преобразование Фурье были созданы для изучения
распространения тепла в твердых и жидких средах. Фурье всю жизнь
исследовал тепловые процессы. Один из опытов был посвящен распространению тепла по якорному кольцу (железному кольцу, к которому крепится якорь), погружаемому на некоторое время наполовину в раскаленные угли. Когда часть кольца раскаляется докрасна, его вынимают из огня. Чтобы тепло не успело уйти в воздух, кольцо сразу закапывают в мелкий песок, а затем измеряют температуру на той его части, которая огнём не нагревалась.
4.15. Приложения преобразования Фурье
Слайд 93Page
График изменения температуры плавно нарастает (в холодной части) и
убывает (в раскаленной части) в виде функции синуса (или косинуса).
Синусоида постепенно выравнивается и в конце концов температура по всему кольцу становится одинаковой. Фурье нашел, что первоначальное нерегулярное распределение можно разложить на множество простых синусоид, каждая из которых имеет свой максимум температуры и свою фазу, т.е. начальное положение на кольце. При этом каждая синусоидальная компонента должна изменяться от максимума к минимуму и обратно целое число раз на одном полном обороте по кольцу.
4.15. Приложения преобразования Фурье
Слайд 94Page
Составляющая, которая имеет ровно один период на кольце (время,
за которое тепло проходит полный круг, неизвестно, оно бралось достаточно
произвольно), была названа главной гармоникой, а составляющие с двумя, тремя и более периодами — соответственно второй, третьей и т.д. гармоникой. Так был построен ряд Фурье.
Фурье свёл функцию распределения тепла, трудно поддающуюся математическому описанию, к удобным для анализа суммам синусов и косинусов, эти суммы очень точно описывали распределение тепла.
4.15. Приложения преобразования Фурье
Слайд 95Page
4.15. Приложения преобразования Фурье
Слайд 96Page
В конце XIX века лорд Кельвин применил ряды Фурье как
основу аналогового вычислительного устройства, которое позволяло морякам оценивать высоту приливов
и отливов. Аналоговый вычислитель механически определял наборы амплитуд и фаз по наблюдениям приливных высот в зависимости от времени. Высоты замерялись на протяжении года в данной гавани.
Каждая амплитуда и фаза представляли синусоидальную компоненту функции высоты прилива и были одной из периодических составляющих. Результаты вводились в вычислительное устройство лорда Кельвина, которое синтезировало кривую, предсказывающую высоту прилива как функцию времени на следующий год. Метод оказался настолько успешным, что такие кривые приливов были составлены для всех портов мира.
4.15. Приложения преобразования Фурье
Слайд 97Page
Преобразованием Фурье можно фильтровать фотографии, спутниковые снимки, рентгеновские, магнитно-ядерные,
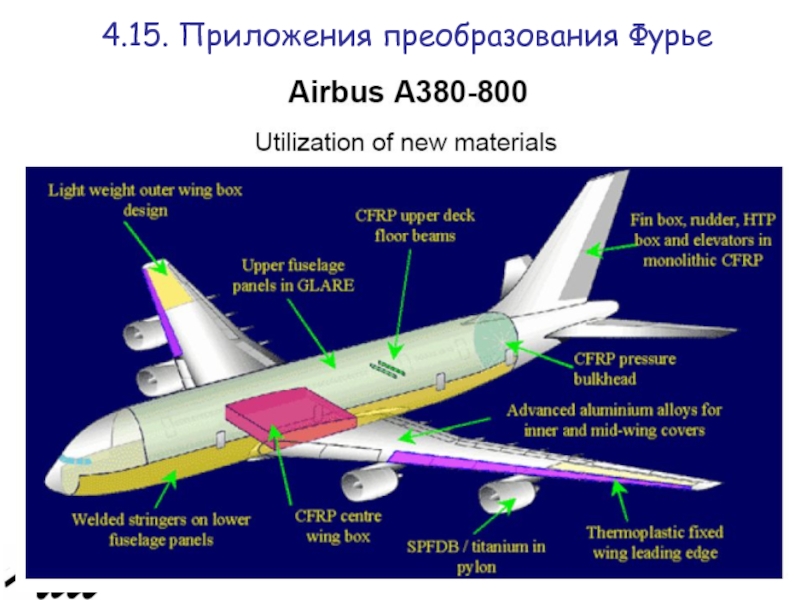
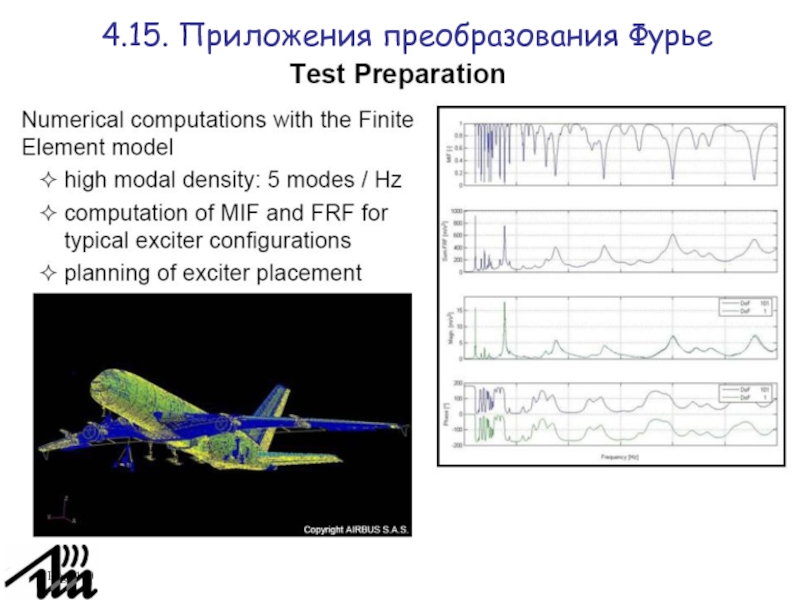
ультразвуковые сканирования органов тела.
Можно изучать вибрацию машин и механизмов, явление
флаттера технических сооружений.
4.15. Приложения преобразования Фурье
Слайд 98Page
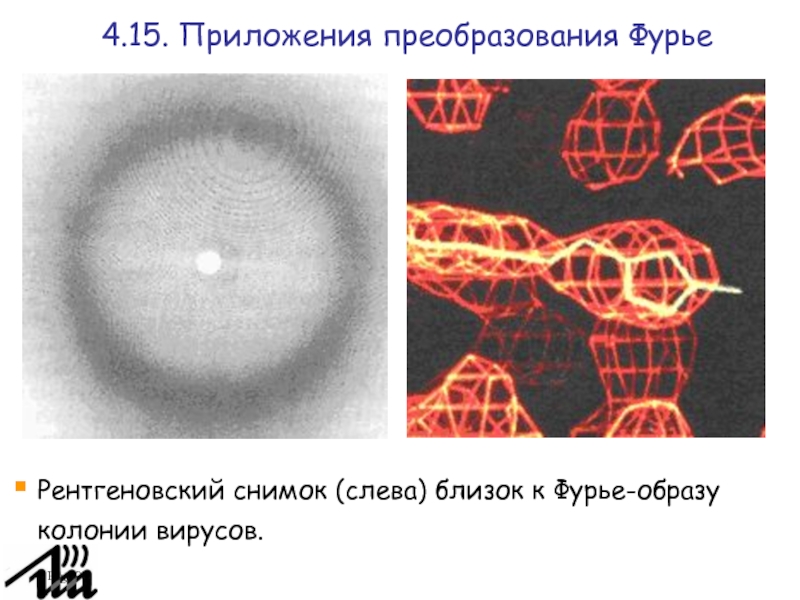
Рентгеновский снимок (слева) близок к Фурье-образу колонии вирусов.
4.15.
Приложения преобразования Фурье
Слайд 99Page
4.15. Приложения преобразования Фурье
Слайд 100Page
4.15. Приложения преобразования Фурье
Слайд 101Page
4.15. Приложения преобразования Фурье
Слайд 102Page
4.15. Приложения преобразования Фурье
Слайд 103Page
4.16. Приложение. Таблица
преобразования Фурье















































![Преобразование Фурье Page Произведение сигнала g(t) на эту функцию4.11. Оконные функции ограничивает сигнал g(t) на интервале [-ε/2, ε/2] Page Произведение сигнала g(t) на эту функцию4.11. Оконные функции ограничивает сигнал g(t) на интервале [-ε/2, ε/2]](/img/thumbs/19865c56068e3597467c80da45c8527e-800x.jpg)

















![Преобразование Фурье Page Пример. Найти диапазон частот W=[-w, +w] такой, что 95% энергии Page Пример. Найти диапазон частот W=[-w, +w] такой, что 95% энергии сигнала](/img/thumbs/3fe3a26b916620235c83e850453ac8c3-800x.jpg)


![Преобразование Фурье Page и получаем два интервала [-4.34, -0.72] и [0.72, 4.34] (в Page и получаем два интервала [-4.34, -0.72] и [0.72, 4.34] (в радианах). В герцах это низкочастотный диапазон](/img/thumbs/f2213fc538615de53ddf1c8b98846dfa-800x.jpg)