Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Презентация книг Редько В. Г. Эволюция, нейронные сети, интеллект. Модели и
Содержание
- 1. Презентация книг Редько В. Г. Эволюция, нейронные сети, интеллект. Модели и
- 2. ПланПроблема происхождения интеллектаКнига 1Модели предбиологической эволюцииМодели адаптивного
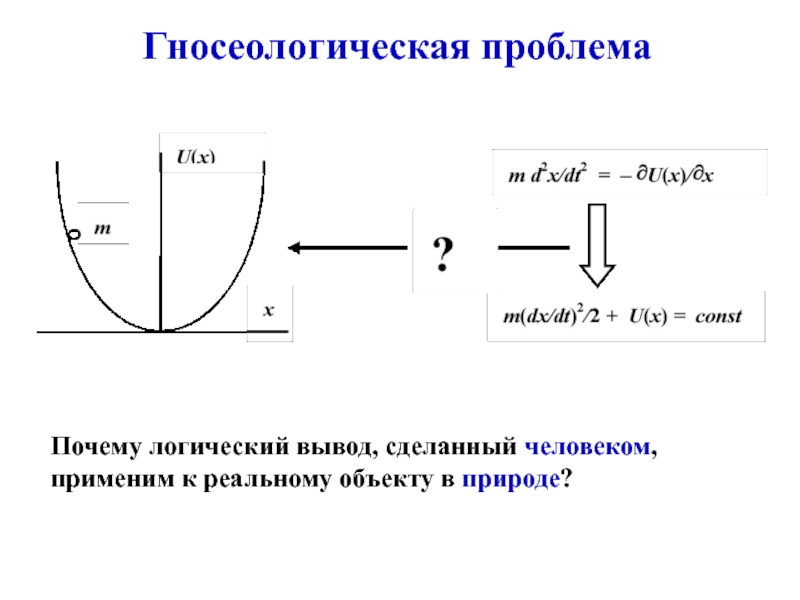
- 3. Гносеологическая проблема Почему логический вывод, сделанный человеком, применим к реальному объекту в природе?
- 4. Гносеологическая проблема « … хотя в начале
- 5. Гносеологическая проблема «Не является ли человеческий разум
- 6. Гносеологическая проблема Уравнения Максвелла Являются законы электродинамики законами природы?
- 7. Подход к исследованию гносеологической проблемыИсследовать происхождение интеллекта
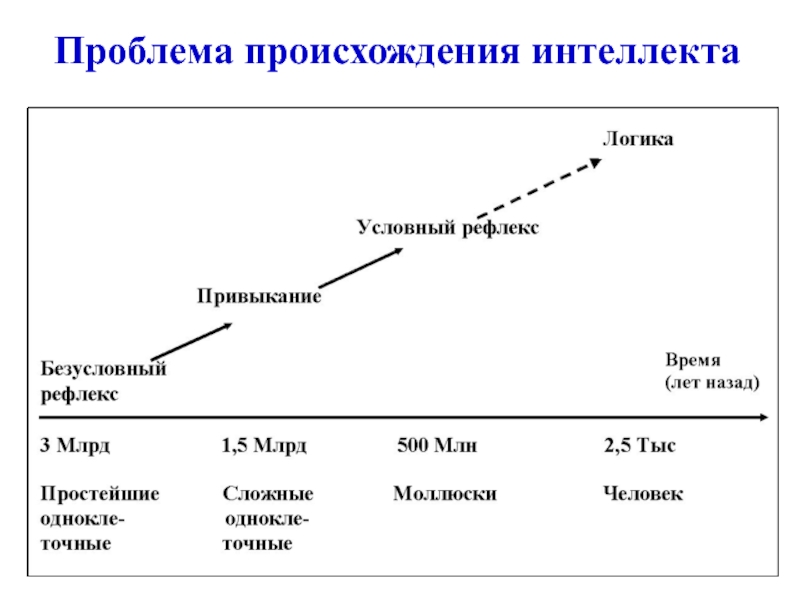
- 8. Проблема происхождения интеллекта
- 9. О биоинформатике (в широком смысле слова)БиологияИнформатикаЧистое
- 10. Три ключевые проблемы1. Проблема происхождения молекулярно-генетических систем
- 11. «Эволюция, нейронные сети, интеллект. Модели и концепции
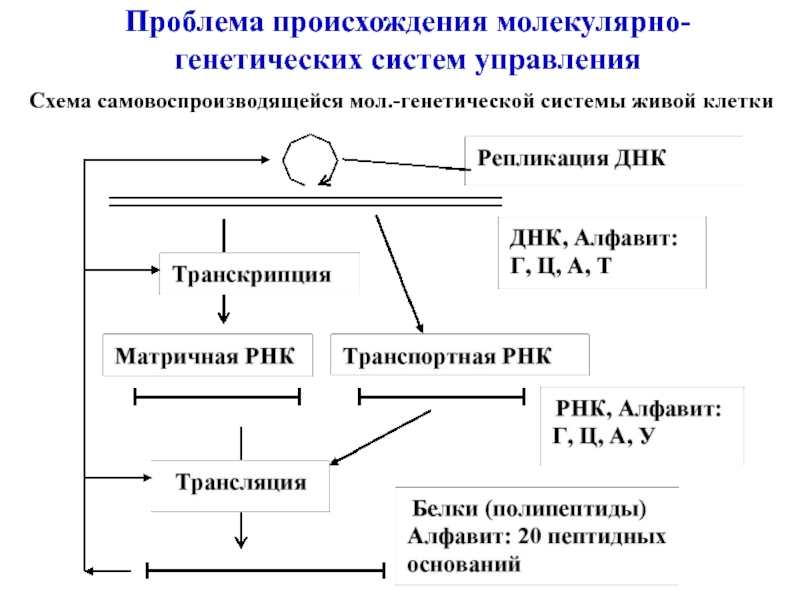
- 12. Проблема происхождения молекулярно-генетических систем управленияСхема самовоспроизводящейся мол.-генетической системы живой клетки
- 13. Проблема происхождения молекулярно-генетических систем управленияМодели происхождения молекулярно-генетических
- 14. Модель квазивидов – эволюция простейших модельных геномовМ.
- 15. Модель квазивидовРассматривается дарвиновская эволюция популяции последовательностей S1
- 16. Схема эволюции в модели квазивидовШаг 0. Формирование
- 17. Отбор пропорционально-вероятностный Доля k-го сектора рулетки qk
- 18. Параметры моделиN - длина последовательности, длина геномаn
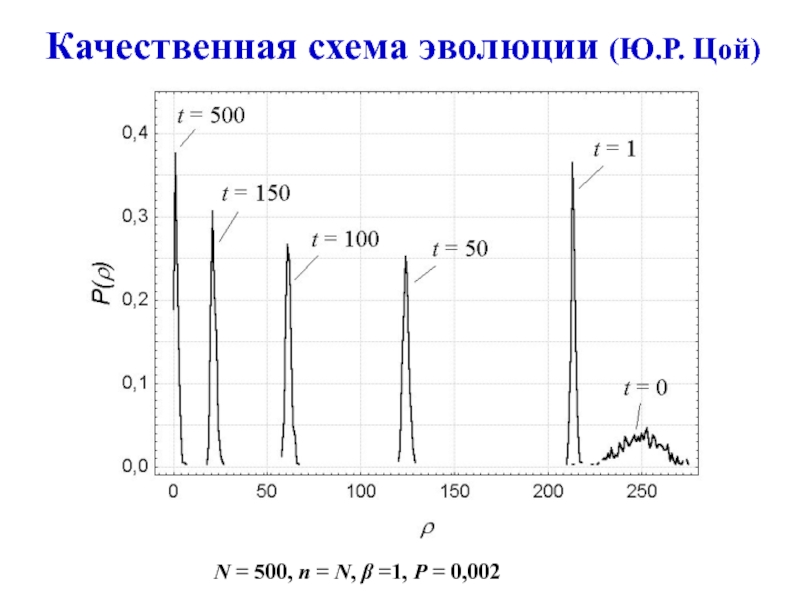
- 19. Качественная схема эволюции (Ю.Р. Цой)N = 500, n = N, =1, P = 0,002
- 20. Качественная схема эволюции Начальное распределение по
- 21. Качественная схема эволюции Для оценки скорости эволюции важна вторая, медленная стадияt1 < t2 < t3
- 22. Роль нейтрального отбора Если численность популяции n
- 23. Аналитическая оценка скорости эволюцииПредполагаем, что роль нейтрального
- 24. Итог оценок Для эволюционного поиска общее число
- 25. Зависимость среднего расстояния до оптимума от номера
- 26. Зависимости времени релаксации TR и времени выхода на стационар TS от N (Ю.Р. Цой, 2005)
- 27. Зависимости времени релаксации TR и времени выхода
- 28. Сравнение с другими алгоритмами Для эволюционного поиска
- 29. Связь с биологической эволюцией С биологической точки
- 30. Проблема происхождения молекулярно-генетических систем управленияМодели происхождения молекулярно-генетических
- 31. Модель гиперциклов – модель кооперации РНК и
- 32. Модель сайзеров – модель самовоспроизводящейся системы (В.А.
- 33. Адаптивный сайзер – модель возникновения адаптивного поведения
- 34. Возможный сценарий возникновения самовоспроизводящейся молекулярно-генетической системы живой клетки
- 35. Адаптивное Поведение From Animal to Animat
- 36. Адаптивное Поведение International Society for Adaptive Behavior
- 37. Исследователи адаптивного поведенияAnimatLab (Paris) (Париж, руководитель –
- 38. Исследователи адаптивного поведенияЛаборатория искусственного интеллекта в университете
- 39. Исследователи адаптивного поведенияЛаборатория искусственной жизни и роботики
- 40. Исследователи адаптивного поведенияЛаборатория интеллектуальных систем(Лозанна, Швейцария, руководитель
- 41. Исследователи адаптивного поведенияИнститут нейронаук Дж. Эдельмана (Калифорния)
- 42. NOMAD (Darwin-VII, способность к обобщению в реальной среде)
- 43. NOMAD (Darwin-X, моделирование поведения мыши в лабиринте
- 44. Исследователи адаптивного поведенияВ.А. Непомнящих. Моделирование спонтанной активности
- 45. Проект "Мозг Анимата". Архитектура многомодульной нейросетевой системы
- 46. Функциональная система по П.К. АнохинуПА – пусковая афферентация, ОА – обстановочная афферентация
- 47. Архитектуры Мозга аниматаВерсии: 2002 – Архитектура на
- 48. Системогенез и архитектура Мозга аниматаТеория системогенеза рассматривает
- 49. Схема обучения Происходит самообучение в соответствии с
- 50. Познание законов природы и Модели «Мозга анимата»Нейронные
- 51. Модели адаптивного поведения в междисциплинарном контекстеМодели адаптивного
- 52. ОТ МОДЕЛЕЙ ПОВЕДЕНИЯ К ИСКУССТВЕННОМУ ИНТЕЛЛЕКТУ(коллективная монография,
- 53. Робот АРНЭ (Л.А.Станкевич, СПГТУ, ОАО «Новая ЭРА», С-Петербург)
- 54. SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06) 25-30 September
- 55. SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06) 25-30 September
- 56. SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06) 25-30 September
- 57. SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06) 25-30 September
- 58. Контуры плана будущих исследованийИсследование нейросетевых схем адаптивного
- 59. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1 Институт оптико-нейронных технологий РАН, Редько Владимир Георгиевич
vgredko@gmail.com
Презентация книг
Редько
Слайд 2План
Проблема происхождения интеллекта
Книга 1
Модели предбиологической эволюции
Модели адаптивного поведения
Книга 2
Впечатление о
конференции Simulation of Adaptive Behavior (SAB’06), Рим, 25 сент. -1
окт. 2006.Слайд 3Гносеологическая проблема
Почему логический вывод, сделанный человеком, применим к реальному
объекту в природе?
Слайд 4Гносеологическая проблема
« … хотя в начале это звучит странно,
но, тем не менее, верно, если я скажу: рассудок не
черпает свои законы (apriori) из природы, а предписывает их ей».
И. Кант. Пролегомены ко всякой будущей метафизике, могущей появиться как наука, 1783 г.
«Наши категории и формы восприятия, данные до индивидуального опыта, адаптированы к внешнему миру точно по той же причине, по какой копыто лошади адаптировано к почве степи и плавник рыбы адаптирован к воде до того, как рыба вылупится из икринки»
К. Лоренц. Кантовская доктрина априорного в свете современной биологии, 1941 г.
Слайд 5Гносеологическая проблема
«Не является ли человеческий разум чем-то таким, что
органически возникло в неразрывной и постоянной причинно-следственной связи с законами
окружающей природы, — точно так же, как это было с человеческим мозгом?Не были бы законы разума, необходимые для априорного мышления, иными, если бы они сформировались иным историческим способом и если бы мы, следовательно, были оснащены иным типом нервной системы?
И вообще, возможно ли, чтобы законы нашего когнитивного аппарата не были связаны с законами реального внешнего мира?
Остается ли орган, развившийся в постоянном взаимодействии с законами природы, настолько независимым, чтобы можно было строить теорию явлений независимо от существования вещи в себе?»
К. Лоренц. Кантовская доктрина априорного в свете современной биологии, 1941 г.
Слайд 6Гносеологическая проблема
Уравнения Максвелла
Являются законы электродинамики законами природы?
Слайд 7Подход к исследованию гносеологической проблемы
Исследовать происхождение интеллекта путем построения математических
и компьютерных моделей когнитивной эволюции, эволюции познавательных свойств биологических организмов
Проследить весь путь биологической эволюции от простейших до человека, анализируя c помощью моделей, как на этом пути возникали свойства познания закономерностей природы в результате развития систем управления адаптивным поведением организмов.
Разумно использовать задел направлений исследований «Адаптивное поведение»
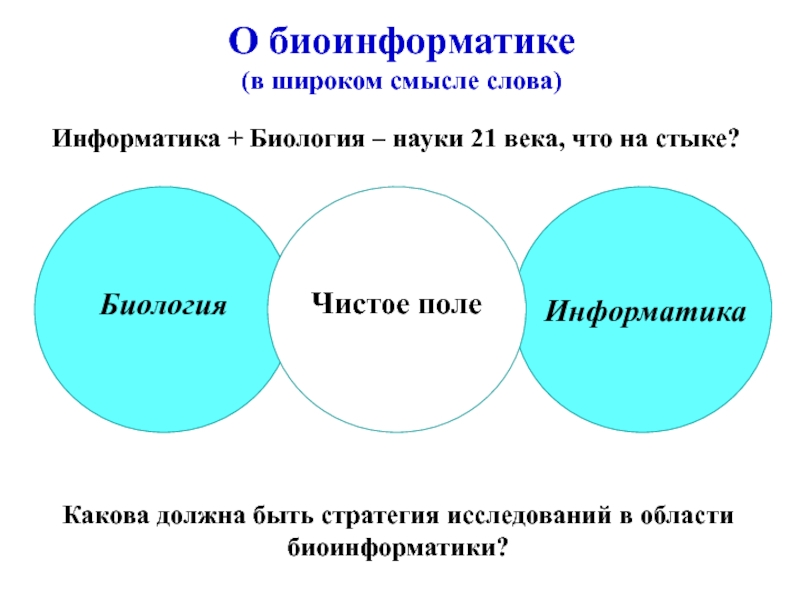
Слайд 9О биоинформатике
(в широком смысле слова)
Биология
Информатика
Чистое поле
Какова должна быть
стратегия исследований в области биоинформатики?
Информатика + Биология – науки 21
века, что на стыке?Слайд 10Три ключевые проблемы
1. Проблема происхождения молекулярно-генетических систем управления – информационно-кибернетические
аспекты проблемы происхождения жизни 2. Проблема происхождения интеллекта человека. Гносеологический
аспект – почему мышление человека применимо к познанию природы, почему в принципе возможна наука? 3. Проблема эволюции человечества в информационном сообществе (применение многоагентного моделирования). Проблема формирования ноосферы Первые две проблемы – фундаментальные, третья – прикладнаяСлайд 11«Эволюция, нейронные сети, интеллект. Модели и концепции эволюционной кибернетики»
Глава 1.
Философские предпосылки эволюционной кибернетики Глава 2. Модели возникновения молекулярно-генетических кибернетических
систем Глава 3. Общие модели молекулярно-генетической эволюции Глава 4. Прикладное эволюционное моделирование Глава 5. Искусственные нейронные сети Глава 6. Направление исследований "Искусственная жизнь" – эволюционные и нейросетевые методы Глава 7. Направление исследований "Адаптивное поведение"Слайд 12Проблема происхождения молекулярно-генетических систем управления
Схема самовоспроизводящейся мол.-генетической системы живой клетки
Слайд 13Проблема происхождения молекулярно-генетических систем управления
Модели происхождения молекулярно-генетических систем управления
Модель квазивидов
– эволюция простейших РНК-цепочек (М. Эйген, 1971) Модель гиперциклов –
модель кооперации РНК и ферментов (М. Эйген, П. Шустер, 1979) Модель сайзеров – модель самовоспроизводящейся системы, модель простейшей протоклетки (В.А. Ратнер, В.В. Шамин, 1980) Адаптивный сайзер – модель молекулярно-генетической системы управления на предбиологическом уровне (В.Г. Редько, 1986) Возможный сценарий возникновения самовоспроизводящейся молекулярно-генетической системы живой клетки:Слайд 14Модель квазивидов – эволюция простейших модельных геномов
М. Эйген, Г. Кун,
Дж. Эдельман
Рассматривается дарвиновская эволюция популяции модельных геномов. Длина генома
равна N, учитываются точечные мутации, скрещивания нетИмеется один оптимум. Рассматривается процесс, который сходится к квазивиду – распределению особей в окрестности оптимума.
Сделаны аналитические оценки, которые демонстрируют, что в эволюционном процессе «оптимальный» геном длины N можно найти при испытании порядка N 2 особей
Оценки проверены путем компьютерного моделирования.
Слайд 15Модель квазивидов
Рассматривается дарвиновская эволюция популяции последовательностей S1 , S2 ,
... , Sn .
Ski = 1, -1; k =
1,2,…, n; i = 1,2,…, N. Длина последовательностей N и численность популяции n велики: N, n >> 1. N = const, n = const.
Имеется оптимальная последовательность Sm , имеющая максимальную приспособленность. Приспособленность произвольной особи S определяется расстоянием по Хеммингу (S, Sm) между S и Sm (числом несовпадающих символов в соответствующих позициях последовательностей):
f(S) = exp[-(S, Sm)], (1)
– интенсивность отбора.
Слайд 16Схема эволюции в модели квазивидов
Шаг 0. Формирование начальной популяции {Sk
(0)}. Для каждого k = 1, ..., n, и для
каждого i = 1 , ..., N , выбираем случайно символ Ski , полагая его равным +1 либо -1.Шаг 1. Отбор
Подшаг 1.1. Расчет приспособленностей. Для каждого Sk из {Sk(t)} вычисляем величину f(Sk), t – номер поколения, k =1, ..., n.
Подшаг 1.2. Формирование новой популяции {Sk(t+1)}. Отбираем n особей в новую популяцию {Sk(t+1)} с вероятностями, пропорциональными f(Sk).
Шаг 2. Мутации особей в новой популяции. Для каждого k = 1, ..., n, для каждого i = 1, ..., N, меняем знак Ski(t+1) на противоположный с вероятностью P .
P - интенсивность мутаций.
Слайд 17Отбор пропорционально-вероятностный
Доля k-го сектора рулетки
qk = fk [S
l fl ]-1 , fk = f(Sk) .
Ровно n
раз крутим рулетку, номер сектора определяет номер особи, выбираемой в популяцию следующего поколения. Для каждого вращения вероятность k-й особи попасть в следующее поколение пропорциональна ее приспособленности fk .
Показан пример, для которого n = 4,
f1 = 1/2, f2 = 1, f3 = 1/4, f4 = 1/4.
Слайд 18Параметры модели
N - длина последовательности, длина генома
n - численность популяции
- интенсивность отбора
P - интенсивность мутаций
N, n >> 1,
> PN, PN < 1Слайд 20Качественная схема эволюции
Начальное распределение по в популяции близко
к нормальному, = N/2, D = N/4.
На первой
стадии происходит отбор особей, расположенных "на левом крыле" исходного распределения, и распределение сжимается.На второй стадии появление новых особей в популяции ограничено мутациями.
Окончательное распределение есть квазивид - распределение в окрестности = 0.
При малых интенсивностях отбора и мутаций (1 >> > PN) распределение в квазивиде близко к распределению Пуассона, <> = D = PN/ .
Слайд 21Качественная схема эволюции
Для оценки скорости эволюции важна вторая, медленная
стадия
t1 < t2 < t3
Слайд 22Роль нейтрального отбора
Если численность популяции n мала, то эволюционный
процесс существенно стохастический и особи могут фиксироваться в популяции случайно,
независимо от их приспособленностей.Роль нейтрального отбора исследовалась в работах М. Кимуры [1], было показано, что характерное время Tn (число поколений) нейтрального отбора составляет порядка численности популяции n
1. Кимура М. Молекулярная эволюция: теория нейтральности. М.: Мир, 1985, 400 с.
Слайд 23Аналитическая оценка скорости эволюции
Предполагаем, что роль нейтрального отбора невелика:
Tn >~
T , (2)
T - характерное время эволюции, Tn ~ n .
Характерное
время t-1, за которое среднее по популяции расстояние до оптимума <> уменьшается на 1, составляет: t-1 ~ tм + tот , tм ~ (NP) -1 , tот ~ b -1
tм – характерное время мутаций , tот - характерное время отбора.
Отсюда для T ~ t-1 N имеем:
T ~ P -1 + N -1. (3)
Считаем отбор достаточно интенсивным: T ~ P -1 и мутации «оптимальными» (одна мутация на геном) P ~ N -1. Тогда T ~ N.
Пусть (2) выполняется на пределе Tn ~ T , тогда n ~ Tn ~ T ~ N.
Общее число особей, участвующих в эволюции, равно n T ~ N 2
Слайд 24Итог оценок
Для эволюционного поиска общее число особей, участвующих в
процессе поиска оптимального генома, составляет nобщ = n T ~
N 2Оценки были сделаны при достаточно разумном выборе параметров:
1) >= 1 - интенсивность отбора достаточно велика
2) P ~ N -1 - мутации «оптимальны» (одна мутация на геном)
3) n ~ N - условие пренебрежения нейтральным отбором выполняется «на пределе»
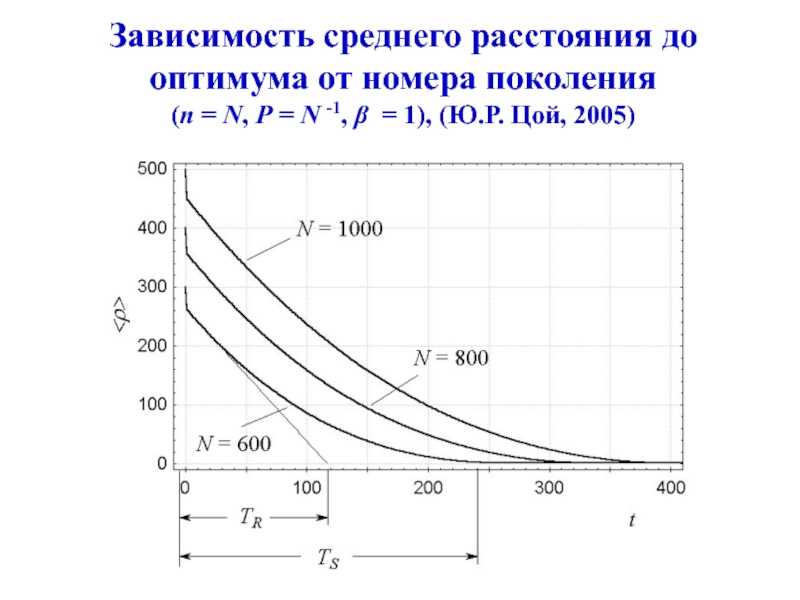
Слайд 25Зависимость среднего расстояния до оптимума от номера поколения
(n = N,
P = N -1, = 1), (Ю.Р. Цой, 2005)
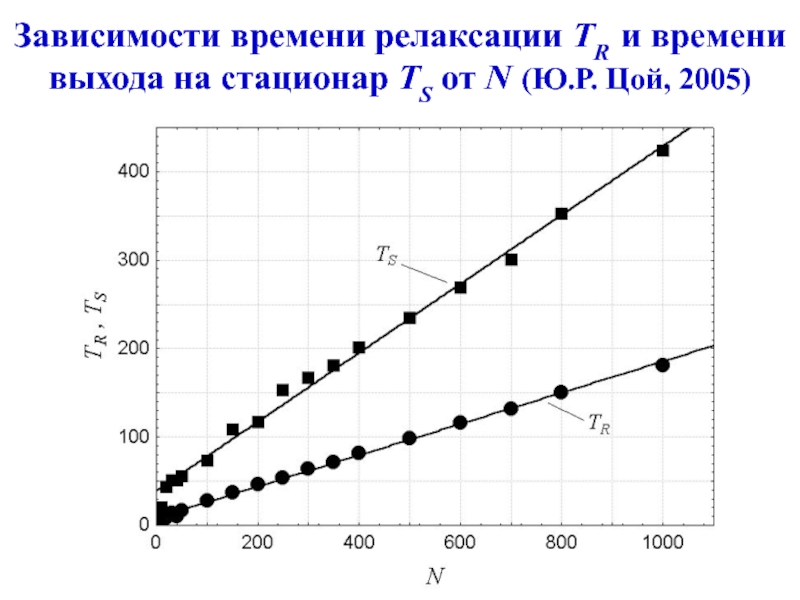
Слайд 27Зависимости времени релаксации TR и времени выхода на стационар TS
от N
При достаточно больших N имеем:
TR (N) = kRN
+ TR0TS (N) = kSN + TS0,
где kR = 0,1772, kS = 0,3903
TR0 = 8.2709, TS0 = 38.7356
Аналитическая оценка T ~ N
Слайд 28Сравнение с другими алгоритмами
Для эволюционного поиска общее число особей,
участвующих в процессе поиска оптимального генома, составляет nобщ = n
T ~ N 2(n ~ N, P ~ N -1, >= 1)
Для последовательного поиска (последовательный перебор символов одной последовательности) nобщ = N.
Для случайного перебора nобщ = 2N .
Слайд 29Связь с биологической эволюцией
С биологической точки зрения модель квазивидов
может рассматриваться только как очень грубое приближение. Тем не менее,
сопоставим цифры.Для бактерии E-coli число нуклеотидов равно 4·106, т.е. порядка N =107 бит, для человека число нуклеотидов равно 3·109, т.е. порядка N =1010 бит.
Жизнь бактерии ~ 1 час.
«Оптимальную» бактерию в популяции 107 особей можно найти за 1000 лет.
Жизнь млекопитающего ~ 1 год.
«Оптимального» млекопитающего в популяции 1010 особей можно найти за 1010 лет.
Полученные оценки дают аргументы в пользу возможности происхождения организмов путем дарвиновской эволюции.
Слайд 30Проблема происхождения молекулярно-генетических систем управления
Модели происхождения молекулярно-генетических систем управления
Модель квазивидов
– эволюция простейших РНК-цепочек (М. Эйген, 1971) Модель гиперциклов –
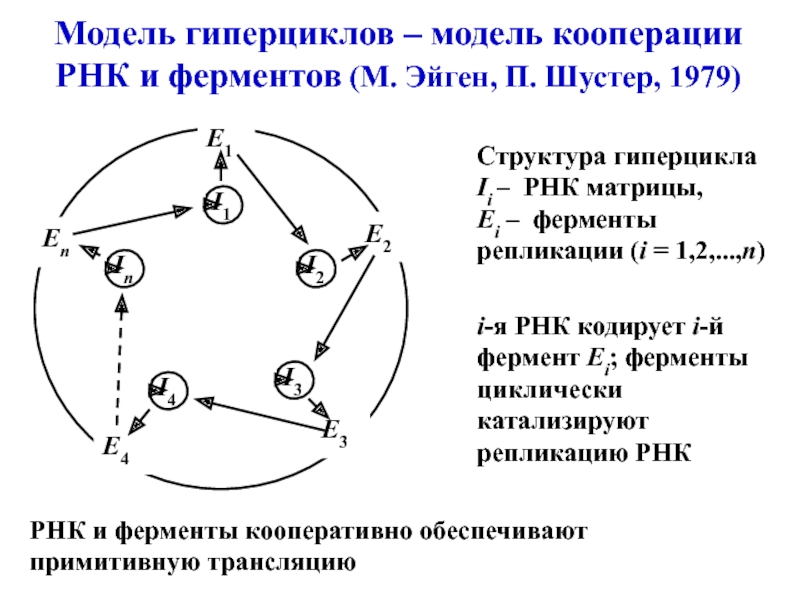
модель кооперации РНК и ферментов (М. Эйген, П. Шустер, 1979) Модель сайзеров – модель самовоспроизводящейся системы, модель простейшей протоклетки (В.А. Ратнер, В.В. Шамин, 1980) Адаптивный сайзер – модель молекулярно-генетической системы управления на предбиологическом уровне (В.Г. Редько, 1986) Возможный сценарий возникновения самовоспроизводящейся молекулярно-генетической системы живой клетки:Слайд 31Модель гиперциклов – модель кооперации РНК и ферментов (М. Эйген,
П. Шустер, 1979)
Структура гиперцикла
Ii – РНК матрицы,
Ei
– ферменты репликации (i = 1,2,...,n)i-я РНК кодирует i-й фермент Ei; ферменты циклически катализируют репликацию РНК
РНК и ферменты кооперативно обеспечивают примитивную трансляцию
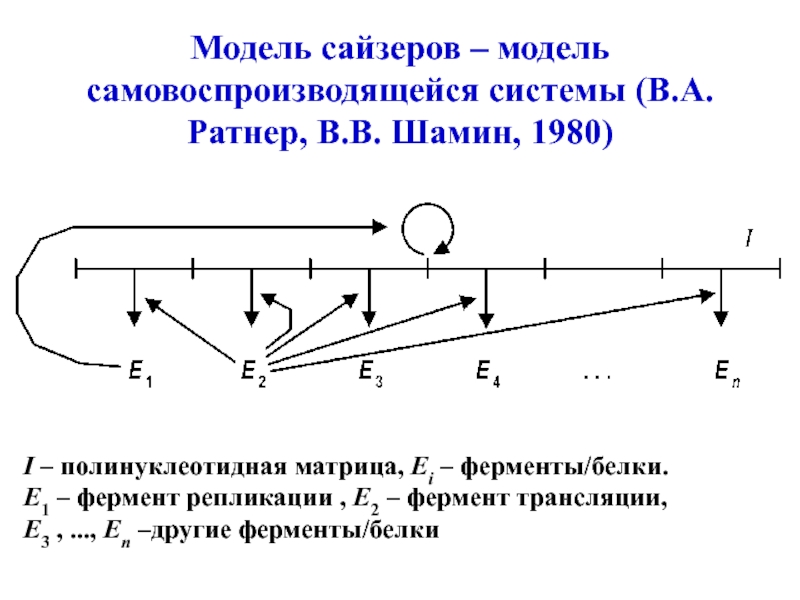
Слайд 32Модель сайзеров – модель самовоспроизводящейся системы (В.А. Ратнер, В.В. Шамин,
1980)
I – полинуклеотидная матрица, Ei – ферменты/белки.
E1 – фермент
репликации , E2 – фермент трансляции,
E3 , ..., En –другие ферменты/белки
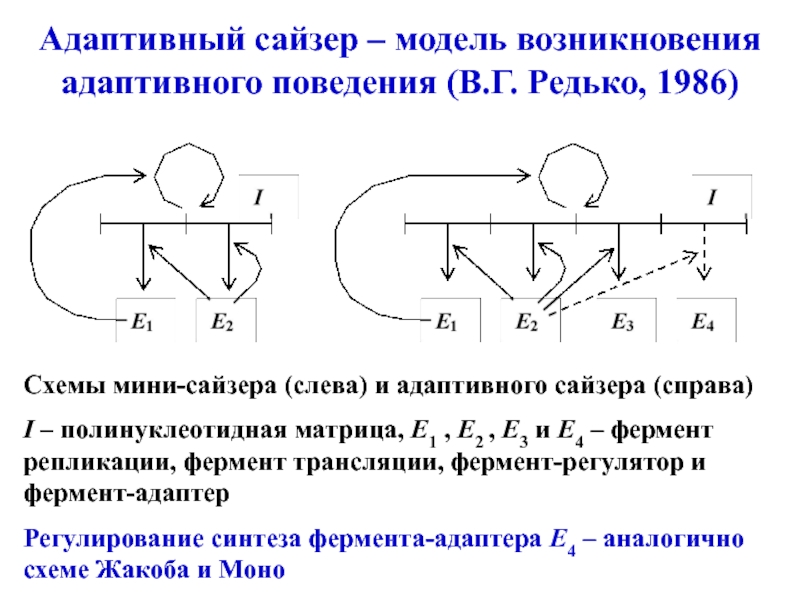
Слайд 33Адаптивный сайзер – модель возникновения адаптивного поведения (В.Г. Редько, 1986)
Схемы
мини-сайзера (слева) и адаптивного сайзера (справа) I – полинуклеотидная матрица, E1
, E2 , E3 и E4 – фермент репликации, фермент трансляции, фермент-регулятор и фермент-адаптер Регулирование синтеза фермента-адаптера E4 – аналогично схеме Жакоба и МоноСлайд 34Возможный сценарий возникновения самовоспроизводящейся молекулярно-генетической системы живой клетки
Слайд 35Адаптивное Поведение From Animal to Animat – модели адаптивного поведения
животного и робота
Первая конференция: Париж, 1990 г. (Ж.-А.
Мейер, С. Вильсон)Основной подход – конструирование и исследование искусственных (в виде компьютерной программы или робота) "организмов" (аниматов, агентов), способных приспосабливаться к внешней среде.
ANIMAL + ROBOT = ANIMAT
Программа-минимум – исследовать архитектуры и принципы функционирования, которые позволяют животным или роботам жить и действовать в переменной внешней среде.
Программа-максимум – попытаться проанализировать эволюцию когнитивных способностей животных и эволюционное происхождение человеческого интеллекта.
Предшественники: М.Л. Цетлин, М.М. Бонгард. Гаазе-Рапопорт М.Г., Поспелов Д.А. От амебы до робота: модели поведения. М.: Наука, 1987.
Слайд 36Адаптивное Поведение
International Society for Adaptive Behavior
http://www.isab.org/
Журнал Adaptive Behavior
Конференции
SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06)
25-30 September 2006, Roma, Italy
Слайд 37Исследователи адаптивного поведения
AnimatLab (Paris)
(Париж, руководитель – один из инициаторов
анимат-подхода Ж.-А. Мейер)
Широкий спектр исследований адаптивных роботов и адаптивного поведения
животных. Подход AnimatLab предполагает, что система управления анимата может формироваться и модифицироваться посредством
1) обучения,
2) индивидуального развития (онтогенеза) и
3) эволюции.
http://animatlab.lip6.fr/index.en.html
Слайд 38Исследователи адаптивного поведения
Лаборатория искусственного интеллекта в университете Цюриха (руководитель Рольф
Пфейфер)
Основной подход – познание природы интеллекта путем его создания
("understanding by building"). Подход включает в себя
1) построение моделей биологических систем,
2) исследование общих принципов естественного интеллекта животных и человека,
3) использование этих принципов при конструировании роботов и других искусственных интеллектуальных систем.
Pfeifer R., Scheier C., Understanding Intelligence. MIT Press, 1999.
http://www.ifi.unizh.ch/groups/ailab/
Слайд 39Исследователи адаптивного поведения
Лаборатория искусственной жизни и роботики в
Институте когнитивных
наук и технологий
(Рим, руководитель Стефано Нолфи)
Исследования в области
эволюционной роботики и принципов формирования адаптивного поведения.Nolfi S., Floreano D. Evolutionary Robotics: The Biology, Intelligence, and Technology of Self-Organizing Machines. Cambridge, MA: MIT Press/Bradford Books, 2000.
http://gral.ip.rm.cnr.it/
Слайд 40Исследователи адаптивного поведения
Лаборатория интеллектуальных систем
(Лозанна, Швейцария, руководитель Дарио Флориано)
Миссия
лаборатории – исследовать и воспроизвести принципы, которые позволяют живым и
искусственным организмам приспосабливаться к переменной и неизвестной внешней средеОсобый акцент на исследование взаимодействий в коллективах роботов
http://lis.epfl.ch
Слайд 41Исследователи адаптивного поведения
Институт нейронаук Дж. Эдельмана (Калифорния)
http://www.nsi.edu/
Направление исследований -
поколения моделей мозга:
Darwin-1, Darwin-2, …, Darwin-XI
NOMAD: Neurally Organized Mobile
Adaptive Device:http://vesicle.nsi.edu/nomad/
1. The device needs to be situated in a physical environment
2. The device needs to engage in a behavioral task
3. The device’s behavior must be controlled by a simulated nervous system having a design that reflects the brain’s architecture and dynamics
4. The behavior of the device and the activity of its simulated nervous system must allow comparisons with empirical data
Слайд 43NOMAD (Darwin-X, моделирование поведения мыши в лабиринте Морриса)
50 нейронных областей,
90000 нейронов,
1.4·106 синапсов
Neuroinformatics, 2005, Vol.3, No 3, PP. 197-221
Слайд 44Исследователи адаптивного поведения
В.А. Непомнящих. Моделирование спонтанной активности животных на основе
анимат-подхода
А.А. Жданов. Схемы и модели автономного адаптивного управления на базе
аппарата эмоций. Накопление знаний - одна главных компонент адаптивного управленияА.И. Самарин. Самообучающиеся роботы (с 1970-х годов)
К.В. Анохин. Нейробиологические подходы к исследованию аниматов
Л.А. Станкевич. Первые в России антропоморфные роботы. Нейрологические архитектуры систем управления гуманоидных роботов на базе когнитивных агентов
В.Г. Редько, М.С. Бурцев, О.П. Мосалов. Модели адаптивного поведения на базе эволюционных и нейросетевых подходов
Слайд 45Проект "Мозг Анимата".
Архитектура многомодульной нейросетевой системы управления анимата на
базе теории ФС
П.К. Анохина
(Редько В.Г., Анохин К.В., Бурцев М.С.,
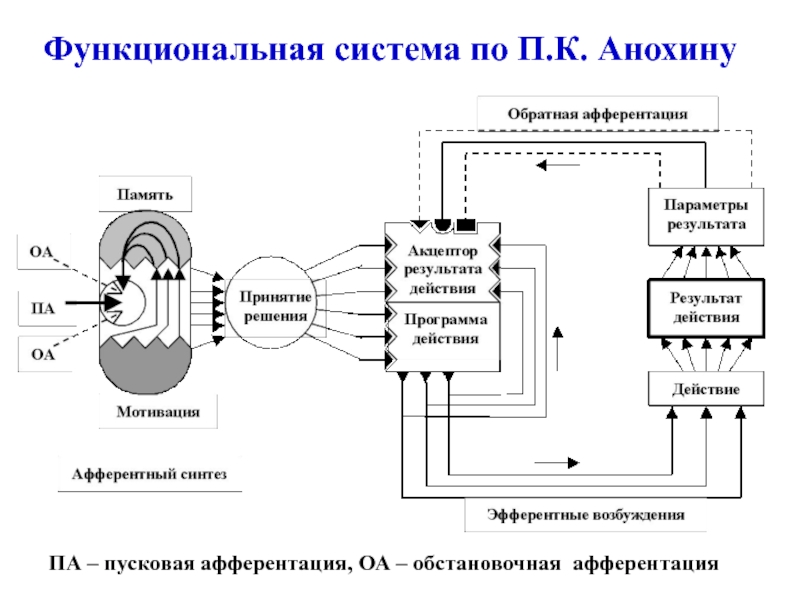
Манолов А.И., Мосалов О.П., Непомнящих В.А., Прохоров Д.В.)Слайд 46Функциональная система по П.К. Анохину
ПА – пусковая афферентация, ОА –
обстановочная афферентация
Слайд 47Архитектуры Мозга анимата
Версии:
2002 – Архитектура на основе метода обратного
распространения ошибки. Есть предсказание будущих ситуаций, обучение – уточнение предсказаний
2004
– Архитектура на основе метода нейросетевых адаптивных критиков. Есть предсказание будущих ситуаций, есть оценка качества предсказываемых ситуаций. Обучение – на основе методов теории обучения с подкреплением2006 – Архитектура на основе нейросетевых модулей, каждый из которых состоит из 1) Контроллера и 2) Модели. Контроллер формирует действия, Модель обеспечивает предсказание. Адаптация происходит путем 1) обучения и эволюции.
Слайд 48Системогенез и архитектура Мозга анимата
Теория системогенеза рассматривает закономерности формирования функциональных
систем (ФС) в эволюции, индивидуальном развитии и обучении
В нашей
модели: Эволюция – источник «первичного» репертуара адаптивного поведения
Обучение – источник «вторичного» репертуара адаптивного поведения
Архитектура системы управления модульная, каждый модуль – отдельная ФС, каждый такт времени t (t = 0,1,2,…) активна только одна ФС, в которой формируется текущее действие и прогноз результата действия. После выполнения действия и прогноза активная ФС передает управление другой ФС.
Слайд 49Схема обучения
Происходит самообучение в соответствии с наградами (положительное подкрепление)
и наказаниями (отрицательное подкрепление).
Есть два режима обучения: грубый поиск и
тонкая доводка.Грубый поиск происходит при существенном рассогласовании прогноза и результата. Тонкая доводка – в остальных случаях.
При грубом поиске происходит реорганизация связей между ФС и формирование новых ФС, этот режим включает существенную случайную составляющую.
В режиме тонкой доводки обучение происходит путем настройки весов синапсов нейронных сетей в ФС, активной в текущий момент времени, и в ФС, бывших активными несколько предыдущих тактов времени. При этом усиливаются/ослабляются связи между входом и выходом в нейронных сетях Контроллеров при положительном/отрицательном подкреплении. Также происходит уточнение прогнозов, формируемых в нейронных сетях Моделей.
Слайд 50Познание законов природы и Модели «Мозга анимата»
Нейронные сети Модели в
архитектуре «Мозга анимата» предназначены для познания закономерностей взаимодействия анимата с
внешней средой.В науке мы строим модели Природы. Пример: уравнения Максвелла – модель электродинамический явлений.
Как перейти от познания простых закономерностей к познанию законов природы?
Возможно ли проследить генезис научных моделей на основе исследований архитектур, подобных «Мозгу анимата»?
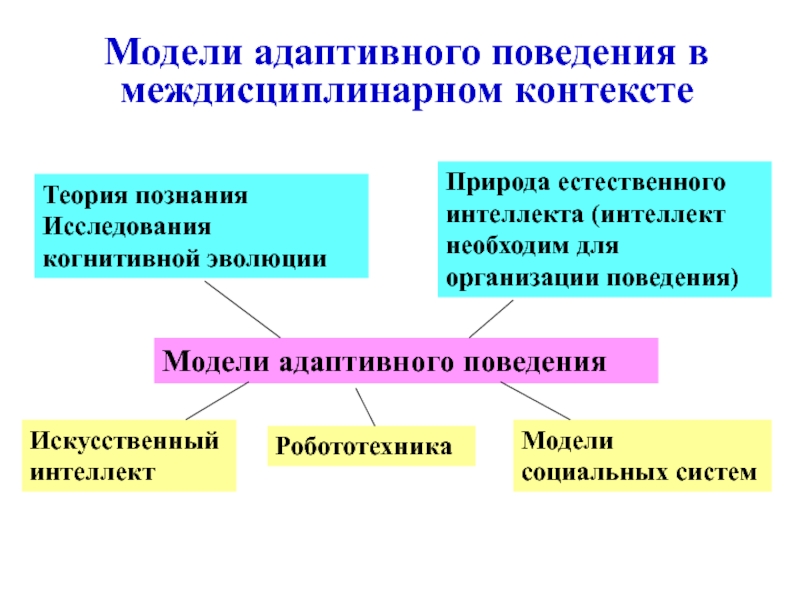
Слайд 51Модели адаптивного поведения в междисциплинарном контексте
Модели адаптивного поведения
Теория познания Исследования
когнитивной эволюции
Природа естественного интеллекта (интеллект необходим для организации поведения)
Модели социальных
системРобототехника
Искусственный интеллект
Слайд 52ОТ МОДЕЛЕЙ ПОВЕДЕНИЯ К ИСКУССТВЕННОМУ ИНТЕЛЛЕКТУ
(коллективная монография, под редакцией В.Г.
Редько, УРСС, 2006)
Часть I. Ретроспектива
П.К. Анохин. Принципиальные вопросы общей теории
функциональных системМ.М. Бонгард и сотр. Проект модели организации поведения - «Животное»
М.Н. Вайцвайг, М.Н. Полякова. Об одном подходе к проблеме создания искусственного интеллекта
А.И. Самарин. Мобильные роботы и самоорганизация в нейронных структурах - ретроспективный взгляд
Часть II. Современные исследования
В.Г. Редько. From Animal to Animat - направление исследований адаптивное поведение
В.А. Непомнящих. Модели автономного поискового поведения
В.Ю. Рощин, А.А. Фролов. Нейросетевая модель выработки пространственной координации на основе сенсомоторного опыта
Д. В. Прохоров. Адаптивные критики и нейронные сети
М.Н. Вайцвайг, М.Н. Полякова. О моделировании мышления
С.В. Корниенко, О.А. Корниенко. Искусственная самоорганизация и коллективный искусственный интеллект: на пути от индивидуума к социуму
А.А. Жданов. Бионический метод автономного адаптивного управления
Л.А. Станкевич. Когнитивный подход к управлению гуманоидными роботами
Слайд 54SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06)
25-30 September 2006, Roma, Italy
Пленарные доклады
Christian
Balkenius "Building Large-Scale Models of Learning and Attention"
Guy Theraulaz "Collective
behaviours in animal societies: a computational approach" George Jeronimis "Biological sensors: Paradigms for Technological Innovation"
Deb Roy "The Whole Linguana"
J. Kevin O'Regan "Why feels feel the way they do: examples from space, color, and touch"
Слайд 55SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06)
25-30 September 2006, Roma, Italy
Секции:
Perception and
Control
The Animat Approach to Adaptive Behavior + Perception and
Control Collective and Social Behaviours
(Neuro)Evolution
Action Selection and Behavioral Sequences + Navigation and Internal World Models
Learning and Adaptation
Adaptive Behaviour in Language and Communication
Special Session: Colette Maloney, Head of Unit E5: Cognition, European Commission, DG Information Society and Media
Слайд 56SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06)
25-30 September 2006, Roma, Italy
Семинары:
1. Swarm
Robotics
2. Behaviour And Mind As A Complex Adaptive System (Fred
Keijzer, Stefano Nolfi, Randal Beer, Frank Pasemann, Dario Floreano, Takashi Ikegami, Jun Tani, Ezequiel di Paolo, Marieke Rohde, Peter Paul Pichler) 3. Evolution And Emergence Of Linguistic Communication
5. Anticipatory Behavior In Adaptive Learning Systems (ABiALS 2006)
4. Bio-inspired Cooperative and Adaptive Behaviours in Robots
6. Adaptive Approaches For Optimizing Player Satisfaction In Computer And Physical Games
7. Multisensory Integration And Concurrent Parallel Memory Systems For Spatial Cognition (Jason G. Fleischer, NSI – “Darwin XI”)
Слайд 57SIMULATION OF ADAPTIVE BEHAVIOR (SAB'06)
25-30 September 2006, Roma, Italy
Workshop 2.
Behaviour And Mind As A Complex Adaptive System
Fred Keijzer. What
are agents anyway? On life, mind and sensorimotor surfacesStefano Nolfi. On the Multi-Level Organization of Behaviour
Randal Beer. Transient dynamics and multiple timescales in brain-body-environment systems
Frank Pasemann. Emergent Neurodynamics and the Accretion of Embodied Cognitive Capacity
Dario Floreano. Enactive Robot Vision
Takashi Ikegami. Homeochaos and Emergence of Sensory motor Couplings
Jun Tani. On the interactions between top-down anticipation and bottom-up regression in cognitive behavior
Ezequiel di Paolo. Sense-making and agency: Being and doing intertwined
Marieke Rohde and Ezequiel Di Paolo. An Evolutionary Robotics Simulation of Human Minimal Social Interaction
Peter Paul Pichler. Towards Minimising Design in a Complex Evolving Ecosystem
Слайд 58Контуры плана будущих исследований
Исследование нейросетевых схем адаптивного поведения на базе
проекта «Мозг Анимата»
Исследование перехода от физического уровня обработки информации в
нервной системе животных к уровню обобщенных образов, уровню понятий (аналогов слов) Исследование процессов формирования причинной связи в памяти животных. Например, связи между условным стимулом (УС) и следующим за ним безусловным стимулом (БС). Анализ роли прогнозов в адаптивном поведении
Исследование процессов формирования логических выводов в «сознании» животных. {УС, УС --> БС} => БС – аналог modus ponens
Исследование коммуникаций, процессов возникновения языка












![Презентация книг Редько В. Г. Эволюция, нейронные сети, интеллект. Модели и Отбор пропорционально-вероятностный Доля k-го сектора рулетки qk = fk [S l Отбор пропорционально-вероятностный Доля k-го сектора рулетки qk = fk [S l fl ]-1 , fk = f(Sk)](/img/thumbs/02181e12465328cf1f8341fa0c065268-800x.jpg)