Презентацию подготовил доцент кафедры Физика РУТ (МИИТ) к.ф.-м.н. Портнов

Иосифович
Рекомендуется в качестве справочного материала для лекторов и ведущих практические

занятия, для проведения физического кружка и
факультативных занятий со студентами,
интересующимися физикой.

Москва, февраль 2018

ЭЛЕКТРОСТАТИКА ДИЭЛЕКТРИКОВ

есть множество исключений, которые будут рассмотрены позже.
Схема а) электронной, б)

ионной и в) дипольно-релаксационной поляризации

Поверхностный заряд, воз-никающий на границе ди-электрика равен потоку вектора поляризации через эту границу.

Поляризация – дипольный момент единицы объёма

σсвяз = ϸn

E = Eo – σ/εo

В идеальном диэлектрике поляриза-ция линейно зависит от поля: ϸ = ϰE

Вводится физическая величина электрическая индукция D = εoEo + ϸ = εoεE , где ε = 1 + ϰ/εo

Граничные условия для поля в диэлектрике:

E1τ = E2τ

D1n = D2n

Диэлектрики

«своб» опускается)
Суммарный связанный заряд диэлектрического тела без включений равен 0
В

дифференциальной форме

Объёмный распределённый связанный заряд возможен лишь для диэлектриков с плавно меняющейся поляризуемостью

εo div E = ρсвоб + ρсвяз

div εoεE =
div D = ρсвоб

- уравнение Максвелла

ρсвяз = – (1 – 1/ε) ρсвоб – εo E grad(ln ε)

Линии D (смеще-ния, индукции) на границе диэлект-рика непрерывны в отличие от линий электрического поля E

Закон преломления линий смещения D на
границе двух диэлектриков

Задачи о поле в диэлектрике инвариантны относительно замены ε → nε

Электрическое поле в диэлектрике

это выражение в СИ
Если эллипсоид имеет полуось a вдоль оси

x. Тогда поле внутри:

где

Дипольный момент:
d = ϸV =4/3πabc εo(ε-1)E (для проводящего эл. ε→∞)

(поперечный разрез)

Расчёт электрических полей в диэлектриках

линейной:

ϸ = ϸo + ϰE

Поляризация в сегнетоэлектриках происходит за счёт увеличения доме-нов, расположенных по полю и уменьшения доменов с поляриза-цией против E.

Сегнетоэлектрики

от поляри-зации P и от E.
Зависимость поляризации  от электрического поля E для

сегнетоэлектрического крис-
талла в полярной фазе; 
а - идеальный кристалл, 
б - реальный сегнетоэлектрик.
Примерный термодинами-ческий потенциал:

В незакороченных образцах разбие-ние на домены энергетически выгодно, т. к. возрастание энергии доменных стенок компенсируется уменьшением энергии электроста-тич. взаимодействия между различ-ными частями кристалла.

механизму фазового перехода сегнетоэлектрики можно разделить на два типа:
1) Сегнетоэлектрики

типа порядок-беспорядок. В кристаллах этого типа имеются дипольные группы, способные вращаться. Фазовый переход и появление спонтанной поляризации связаны с упорядочением диполей, поэтому его называют переходом типа порядок– беспорядок;
2) Сегнетоэлектрики типа смещения. Кристаллы этого типа не содержат атомных групп, обладающих постоянным дипольным моментом. Фазовый переход происходит в результате смещения ионов из некоторого нулевого положения в другое, приводящее к появлению электрических моментов и возникновению спонтанной поляризации. Такой переход называют фазовым переходом типа — смещения. Классическим примером сегнетоэлектрика такого типа является ВаТiO3. На его основе создан большой класс керамических (немонокристаллических) сегнетоэлектриков, имеющих промышленное применение.
Появление большого числа новых материалов, сочетающих в себе различные свойства и получаемых как в виде твердых химических соединений, так и в виде твердых растворов и смесей, позволяет классифицировать сегнетоэлектрики по группам. Это вещества с четко выраженным фазовым переходом, с размытым фазовым переходом, с резко выраженными нелинейными свойствами (вариконды), с полупроводниковыми свойствами, с магнитным упорядочением, сегнетоэлектрики-фотопроводники и т.д.

Расчёт равновесной доменной структуры в сегнетоэлектриках, даже для образцов простейших форм, представляет собой сложную задачу, пока окончательно не решённую. Сложен и ожидаемый характер доменной структуры, согласно теории, она должна измельчаться («ветвиться») вблизи поверхности кристалла.
Однако доменная структура, отвечающая предсказаниям теории для идеального сегнетоэлектрика, практически никогда не наблюдается. При образовании доменной структуры важную роль играет предыстория образца, напр. условия прохождения через точку Кюри Ткв неравновесных условиях при первом охлаждении кристалла после его выращивания при повыш. темп-pax, а также дефекты кристаллич. структуры. Кроме того, во многих сегнетоэлектриках на характер доменной структуры сильное влияние оказывает экранирование электрич. поля за счёт перераспределения свободных носителей заряда и перезарядки локальных центров.

Виды сегнетоэлектриков

ϸx = ϰxxEx +ϰxyEy +ϰxzEz
ϸy = ϰyxEx +ϰyyEy

+ϰyzEz
ϸz = ϰzxEx +ϰzyEy +ϰzzEz

Аналогично записывается связь напряжённости и индукции Dx = εoεxxEx + εoεxyEy + εoεxzEz … и т.д.
В главных осях (если оси координат направлены вдоль главных осей) тензор диэлектрической проницаемости диагональный, т.е. εxx= ε1 , εyy= ε2 , εzz= ε3 , а все остальные – нули. Вычисление индукции проще всего производить в главных осях, а затем переходить обратно в исходную систему координат.

Анизотропные диэлектрики

напряжённости
варикап
Поляризация для системы жёстких незакреплённых диполей описыва-ется функцией Ланжевена:
P =

no po , где

Здесь no - число диполей в едини-
це объёма, po – дипольный момент
жёсткого диполя

С ростом напря-
жения толщина
обеднённого
слоя на p-n
переходе растёт и ёмкость
уменьшается

Пример насыщения диэлектрической проницаемости в воде вблизи йона

вариконды

Диэлектрическое насыщение

1
Диэлектрическая проницаемость смеси веществ с близкими по величине ε,

- аддитивным оказывается кубический корень из ε

Формулы, приведённые в курсе Ландау и Лифшица:

Для мелкодисперсных сильно неоднородных хаотических смесей, а также пористых материалов, используется формула Лихтенэкера

Тензор эффективной диэлектрической про-ницаемости слоистой смеси в главных осях

Не годится для смесей с металлическими включениями

Теория Клаузиуса – Моссотти – Лорентца - Лоренца

Сферические примеси в приближении самосогла-сованного поля

Неравенства для смесей: εсредн.гарм < εeff < εсредн.арифм

, где

При значительном отличии проницаемостей компонен-тов смеси применяется формула Оделевского:

Диэлектрические свойства смесей

в жидком и газообразном диэлектрике
Сила и момент сил, действующие на

диэлектрик, определяются поляризацией

Должно соблюдаться локальное равновесие =>

+ дипольный момент х Е

Пондеромоторные силы

из обкладок. Это приводит к появлению некоторого постоянного заряда конденсатора.

При изменении ёмкости, вследствие смеще-ния мембраны, на конденсаторе появляется изменение на-пряжения, соответствующее акустическому сигналу.

Время,сут
Экспериментальные данные по внутренней релаксации заряда в плёночных электретах
в нормальных условиях:  1 Политетрафтор-этилен, h=50 мкм; 2 Поликарбонат, h=25 мкм 3 Полипропилен, h=20 мкм; 4 Полиэтилен-терефталат,h=25мкм

Электреты

Спектр тока термостимулированной деполяризации фольгирован- ного ФЭП-электрета (алюминий с одной стороны) сразу после поляризации: 1 - заряд электрическим разрядом; 2 - заряд электрическим пучком. Скорость нагрева 4 °С×мин-1 Source: https://worldofmaterials.ru/spravochnik/dielectrics/195-elektrety

стёкол,

под действием дефор-
мации индуцировать электрический за-
ряд на своей поверхности (прямой пье-
зоэффект), либо под влиянием

внешне-
го электрического поля деформировать-
ся (обратный пьезоэффект). Оба эффек-
та открыты братьями Жаком и Пьером
Кюри в 1880—1881 гг.
Пьезоэлектрики широко используются
в современной технике в качестве элемента
 датчика давления.
Существуют пьезоэлектрические детонаторы, источники звука огромной мощности, миниатюрные трансформа-торы, кварцевые резонаторы для высокостабильных генераторов частоты, пьезокерамические фильтры, ультра-звуковые линии задержки и др. Наиболее широкое применение в этих целях кроме кристаллического кварца получила поляризованная пьезокерамика, изготовленная из поликристаллических сегнетоэлектриков, например, из цирконата-титаната свинца.
В быту можно наблюдать пьезоэффект, например, в зажигалке, где искра образуется от нажима на пьезопластинку, а также при медицинской диагностике с помощью УЗИ, в которой используются пьезоэлектрические источник и датчик ультразвука. Передовой областью использования пьезоэлектриков является сканирующая зондовая микроскопия (СЗМ). Из пьезоэлектриков изготавливаются сканирующие элементы зондовых микроскопов, перемещающие зонд в плоскости образца. Наибольшее распространение в ней имеют трубчатые пьезоэлементы. Они позволяют получать достаточно большие перемещения объектов при сравнительно небольших управляющих напряжениях. Они представляют собой полые тонкостенные цилиндры, изготовленные из пьезоэлектрических ма-териалов. Соединение трех таких трубок в единый узел позволяет организовать перемещение зонда в трех орто-гональных направлениях, такой сканирующий элемент называется триподом.
В 1964 г. Ю. В. Гуляев и В. И. Пустовойт предложили слоистую структуру «пьезоэлектрик-полупроводник» в качестве базовой конструкции акустоэлектронных приборов, использующих поверхностно-акустические волны.

Пьезоэлектрики

по частям:

1й интеграл
стремится к 0 (если
это обычный провод
ник), а 2й - пропорционален дипольному моменту области контакта.

Вблизи ребра раздела потенциал зависит толь-ко от угла

Причина образования двойного слоя – неэлектрические сто-ронние силы
Ze φab = Wa – Wb
W – потенциальная энергия

Контактная разность потенциалов

раздвигания тел каждое из них оказывается заряженным
Электризация воды и парафинового

шарика, погруженного в нее

Электризация трением

подобен плоскому конденсатору с постоян-ными характеристиками.
Теория

Гуи-Чепмена:
противо-йоны, благодаря тепло-вому движению, образуют вбли-зи электрода диффузную ионную
атмосферу

Теория Штерна:
учёт и того, и другого

Толщина адсорб-ционного слоя d определяется раз-мерами противо-ионов, обычно она незначительна и не превышает 1 нм. 

Строение коллоидной ми-целлы по Н.И. Горбунову

Уравнение Гуи

В адсорбци-онном слое находятся дегидрати-рованные ионы

ze – заряд частиц
со - концентрация

Электролиты в электрическом поле

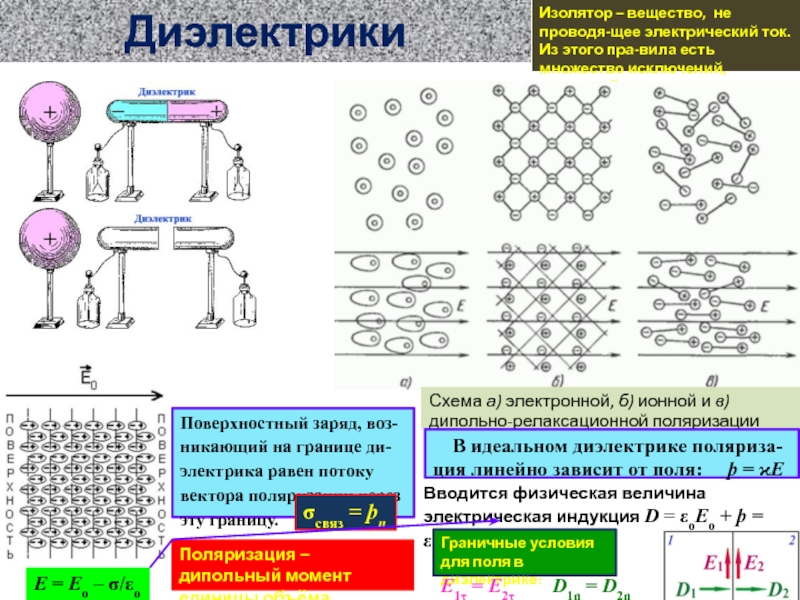
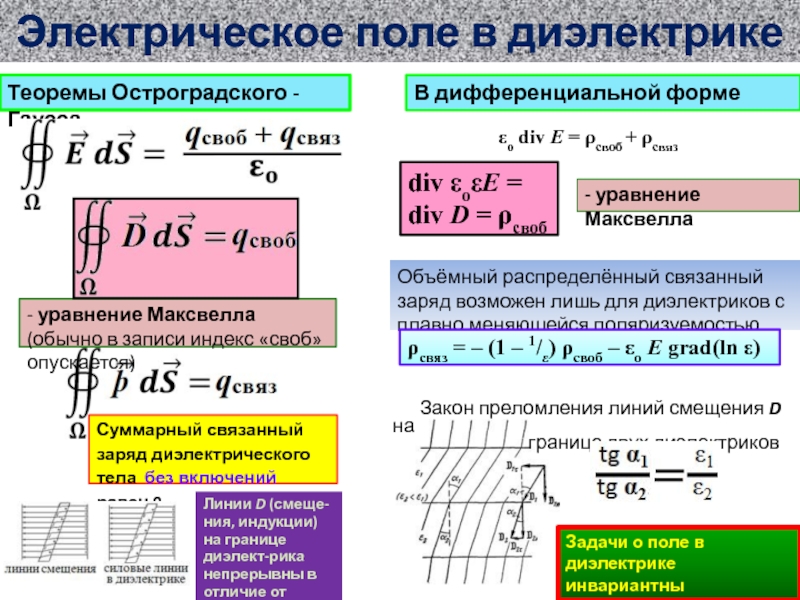
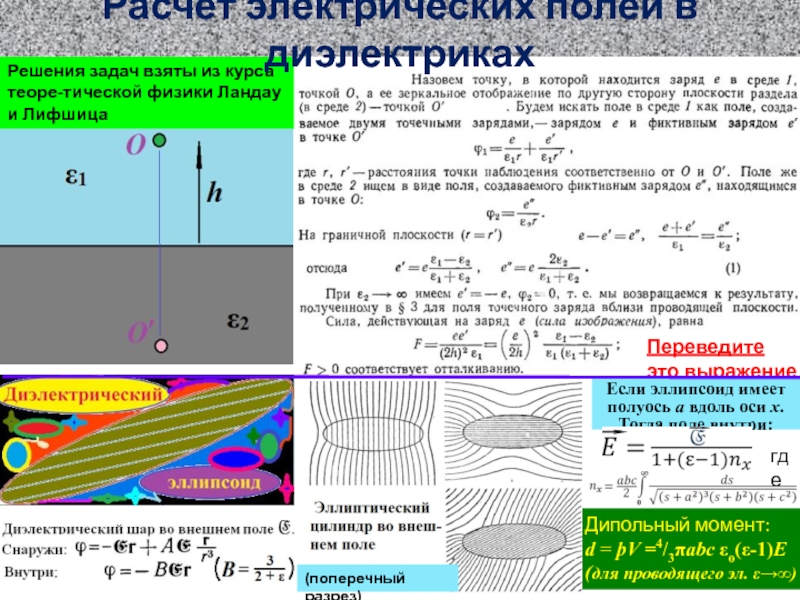
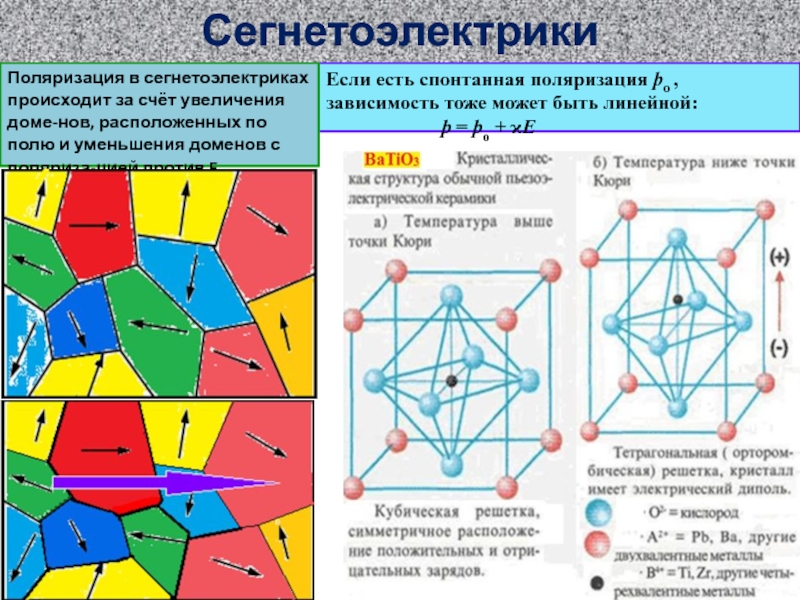
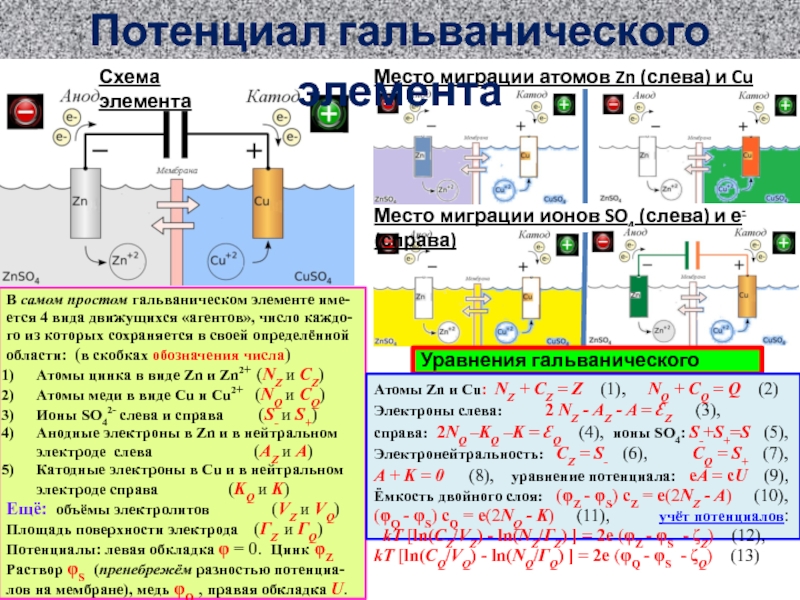
ионов SO4 (слева) и е- (справа)
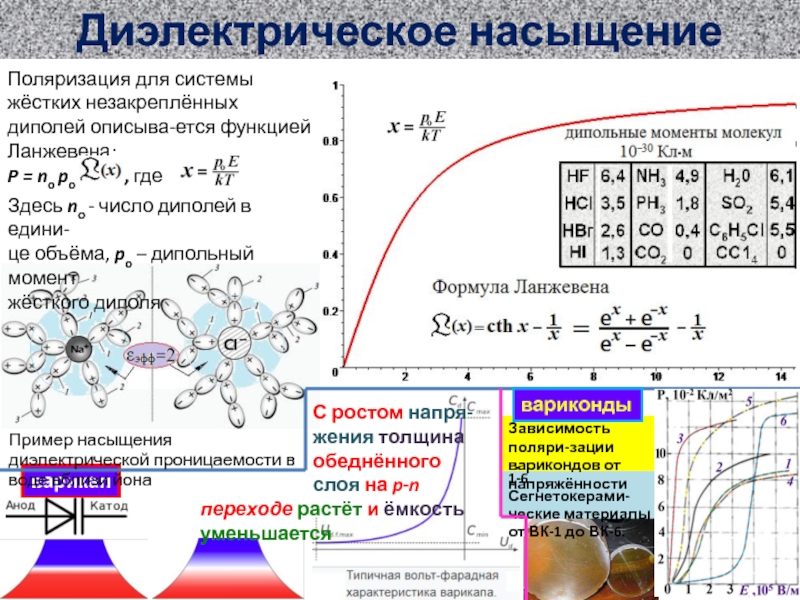
В самом простом гальваническом элементе

име-ется 4 вида движущихся «агентов», число каждо-го из которых сохраняется в своей определённой области: (в скобках обозначения числа)
Атомы цинка в виде Zn и Zn2+ (NZ и CZ)
Атомы меди в виде Cu и Cu2+ (NQ и CQ)
Ионы SO42- слева и справа (S- и S+)
Анодные электроны в Zn и в нейтральном электроде слева (AZ и A)
Катодные электроны в Cu и в нейтральном электроде справа (KQ и K)
Ещё: объёмы электролитов (VZ и VQ)
Площадь поверхности электрода (ГZ и ГQ)
Потенциалы: левая обкладка φ = 0. Цинк φZ
Раствор φS (пренебрежём разностью потенциа-лов на мембране), медь φQ , правая обкладка U. Ёмкость конденсатора c, дв.эл.слоёв cZ и cQ
хим.потенциалы ζZ и ζQ

Уравнения гальванического элемента

Атомы Zn и Cu: NZ + CZ = Z (1), NQ + CQ = Q (2)
Электроны слева: 2 NZ - AZ - A = ƐZ (3),
справа: 2NQ –KQ –K = ƐQ (4), ионы SO4: S-+S+=S (5),
Электронейтральность: CZ = S- (6), CQ = S+ (7),
A + K = 0 (8), уравнение потенциала: eA = cU (9),
Ёмкость двойного слоя: (φZ - φS) cZ = e(2NZ - A) (10),
(φQ - φS) cQ = e(2NQ - K) (11), учёт потенциалов:
kT [ln(CZ/VZ) - ln(NZ/ГZ) ] = 2e (φZ - φS - ζZ) (12),
kT [ln(CQ/VQ) - ln(NQ/ГQ) ] = 2e (φQ - φS - ζQ) (13)

Потенциал гальванического элемента

премии по химии (1920 г.) «в признание его работ по термодинамике».
Занимался изучением

смешанного воздействия магнетизма и теплоты на электрический ток.

Луиджи Гальвани 1737-1798 г.г.

Алессандро Вольта 1745-1827 г.г.
Итальянский физик,химик и физиолог, один из основоположников учения об электричестве.
Вольта впервые поместил пластины из цинка и меди в кислоту, чтобы получить непрерывный электрический ток, создав первый в мире химический источник тока.

Итальянский анатом,физиолог ифизик, один из основателей электрофизиологии и учения об электричестве, основоположник экспериментальной электрофизиологии. Обнаружил возникновение разности потенциалов при контакте разных видов металла и электролита.

сохранения энергии, показав его всеобщий характер.
Пьер Кюри 1859-1906 г.г.
Французский учёный-физик,

один из первых исследователей радиоактивности, лауреат Нобелевской премии по физике за 1903 год. 
Открыл пьезоэлектрический эффект, полоний и радий.

Лев Давидович Ландау 1908-1968 г.г.
Советский физик-теоретик, лауреат Нобелевской премии по физике 1962 года за основополагающие теории конденсированной материи, в особенности жидкого гелия. Объяснил сверхтекучесть используя математический аппарат.

Йоханнес Дидерик Ван дер Ваальс 1837-1923 г.г.
Голландский физик, лауреат Нобелевской премии по физике в 1910 г. за работу над уравнением состояния газов и жидкостей.