Приближение функции

Содержание

1. Приближение функции
2. и тогда многочлен (1) примет вид:Многочлен, который
3. Пример. По заданным точкамОпределить интерполяционный многочлен L(x).L(x)=x2
4. functionyr=lagrange(x,y,xz)n=length(x)nz=length(xz)i=1 шаг 1 до nzk=1 шаг 1 до nj=1 шаг 1 до nyr(i)=0pr=1pr=pr*(xz(i)-x(j))/(x(k)-x(j))j~=kyr(i)=yr(i)+pr*y(k)EndBeginEndx,y,xzyzyz=lagrange(x,y,xz)lagrange(x,y,xz)
5. Метод наименьших квадратовПусть данные некоторого эксперимента представлены
6. Функцию f(x,a0,a1,…,am) определим как полином степени m
7. илиНеобходимые условия минимума критерия R имеют вид:
8. Полученную линейную относительно искомых параметров a0,a1,a2, систему
9. При аппроксимации полиномами высших порядков матрица
10. Слайд 10
11. Слайд 11
12. BeginEndm,n,x,ya,dy,ra=inv(F’*F)*F’*yi=1 шаг 1 до nj=1 шаг 1 до mF(i,j)=x(i)^(j-1)yr=F*a; dy=y-yrr=dy’*dycloseplot(x,y,’ko’)hold on plot(xt,yt,’k-’)
13. Скачать презентанцию

и тогда многочлен (1) примет вид:Многочлен, который в n+1 узловой точке будет принимать заданные значения, можно представить как сумму многочленов вида (2).где i = 0,1,2,3,…….,n, который только в точке xi принимает

Слайды и текст этой презентации

Слайд 1Интерполяция.
Метод с использование многочлена Лагранжа.
Пусть в n+1 узловой точке

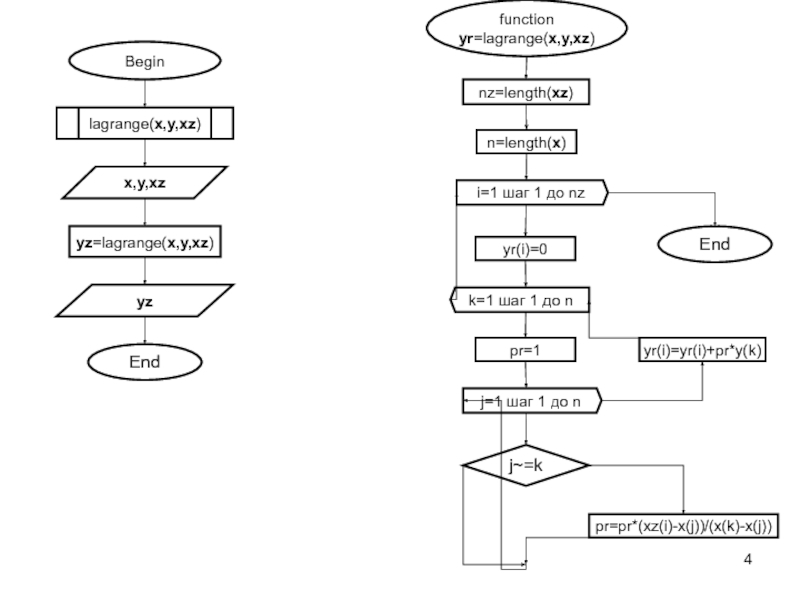
x0, x1, x2, …, xn определены значения y0, y1, y2,

…, yn. Требуется построить многочлен L(x) степени не выше n, который принимает в узловых точках заданные значения, т.е. L(x0)=y0, L(x1)=y1, L(x2)=y2, …, L(xn)=yn.

Определение аналитической зависимости функции, между x и y в виде некоторой функции f(x), которая в узловых точках принимает заданные значения.
f(xi)=yi, где i=0,1,2,…,n .
Интерполяция используется для замены реальной сложной функции более простой на небольшом интервале области определения функции, а также для вычислений промежуточных значений функции заданной таблично.

Приближение функции.

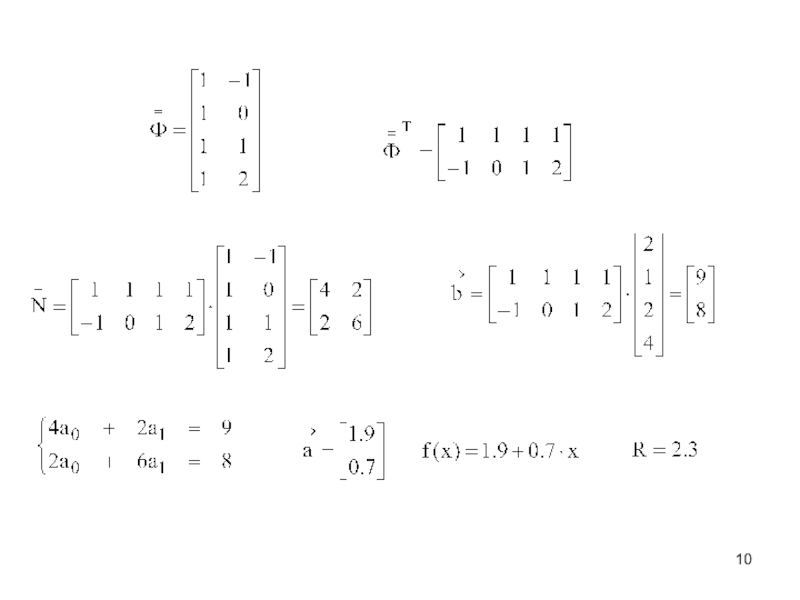
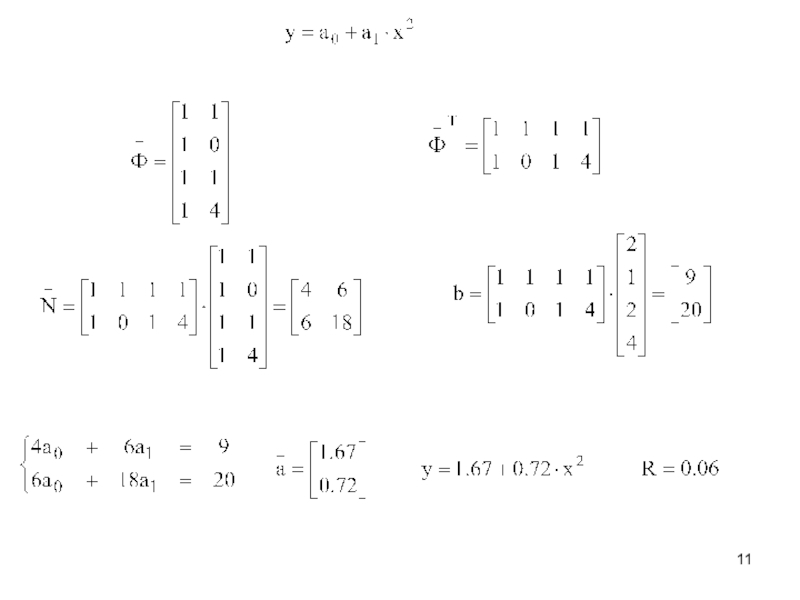
Для заданных значениях независимой переменной xi и соответствующих им значениях зависимой переменной yi (i=0,1,2,…,n) определить аналитическую зависимость. y=f(x)

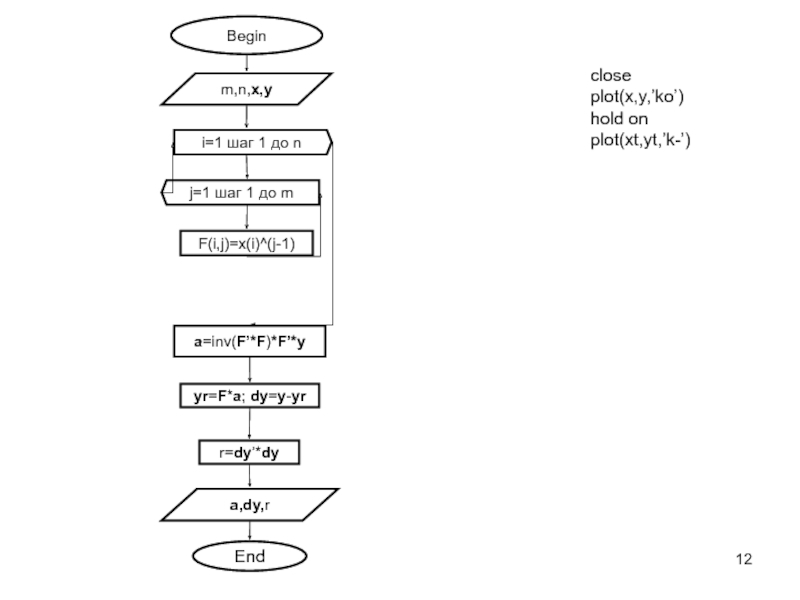
Основные этапы при приближение функции.

Выбор вида зависимости
Выбор критерия
Выбор узловых точек
Оценка точности

Интерполяция.Метод с использование многочлена Лагранжа. Пусть в n+1 узловой точке x0, x1, x2, …, xn определены значения

Слайд 2и тогда многочлен (1) примет вид:

Многочлен, который в n+1 узловой

точке будет принимать заданные значения, можно представить как сумму многочленов

вида (2).

где i = 0,1,2,3,…….,n, который только в точке xi принимает значение yi , а в остальных равен нулю.

из этого условия можно определить ci:

Рассмотрим многочлен вида

и тогда многочлен (1) примет вид:Многочлен, который в n+1 узловой точке будет принимать заданные значения, можно представить

Слайд 3Пример. По заданным точкам
Определить интерполяционный многочлен L(x).

L(x)=x2

Слайд 4function
yr=lagrange(x,y,xz)
n=length(x)
nz=length(xz)
i=1 шаг 1 до nz
k=1 шаг 1 до n
j=1 шаг

1 до n
yr(i)=0
pr=1
pr=pr(xz(i)-x(j))/(x(k)-x(j))
j~=k
yr(i)=yr(i)+pry(k)
End
Begin
End
x,y,xz
yz
yz=lagrange(x,y,xz)
lagrange(x,y,xz)

functionyr=lagrange(x,y,xz)n=length(x)nz=length(xz)i=1 шаг 1 до nzk=1 шаг 1 до nj=1 шаг 1 до nyr(i)=0pr=1pr=pr*(xz(i)-x(j))/(x(k)-x(j))j~=kyr(i)=yr(i)+pr*y(k)EndBeginEndx,y,xzyzyz=lagrange(x,y,xz)lagrange(x,y,xz)

Слайд 5Метод наименьших квадратов
Пусть данные некоторого эксперимента представлены в виде таблицы

значений независимой переменной x и зависимой переменной y:
Требуется отыскать аналитическую

зависимость f(x,a0,a1,…,am), являющуюся функцией одной независимой переменной x и параметров a0,a1,a2,…,am, которая наилучшим образом описывала бы эти экспериментальные данные в смысле минимума квадратичного критерия рассогласования R(a0,a1,…,am):

Аппроксимация.

Метод наименьших квадратовПусть данные некоторого эксперимента представлены в виде таблицы значений независимой переменной x и зависимой переменной

Слайд 6Функцию f(x,a0,a1,…,am) определим как полином степени m вида:
Надо найти такие

значения параметров, при которых квадратичный критерий рассогласования имел бы минимальное

значение

Тогда критерий R будет являться функцией трёх переменных a0,a1,a2 :

Вывод формулы для определения параметров в матричном виде рассмотрим на примере полинома второй степени (m=2).

Функцию f(x,a0,a1,…,am) определим как полином степени m вида:Надо найти такие значения параметров, при которых квадратичный критерий рассогласования

Слайд 7или
Необходимые условия минимума критерия R имеют вид:

Слайд 8Полученную линейную относительно искомых параметров a0,a1,a2, систему уравнений запишем в

матричном виде:
где
Для удобства формирования матрицы коэффициентов
и столбца свободных

членов

элементы которой определяются

введем матрицу

тогда

через значения независимой переменной xi, i=0,1,2,…,n

Полученную линейную относительно искомых параметров a0,a1,a2, систему уравнений запишем в матричном виде: гдеДля удобства формирования матрицы коэффициентов

Слайд 9При аппроксимации полиномами высших порядков матрица

будет иметь вид:
Пример. Определить параметры зависимости вида
используя метод наименьших

квадратов, по следующим экспериментальным данным:

В общем случае
количество строк в матрицы равно количеству точек, а количество столбцов равно количеству параметров, где строка состоит из значений частных производных от функции f(x,a0,a1,…,am) по соответствующему параметру.

При аппроксимации полиномами высших порядков матрица будет иметь вид:Пример. Определить параметры зависимости вида

Слайд 10

Слайд 11

Слайд 12Begin
End
m,n,x,y
a,dy,r
a=inv(F’F)F’y
i=1 шаг 1 до n
j=1 шаг 1 до m
F(i,j)=x(i)^(j-1)
yr=Fa; dy=y-yr
r=dy’*dy
close
plot(x,y,’ko’)
hold

on
plot(xt,yt,’k-’)

Скачать презентацию

Разделы презентаций

Приближение функции

Содержание

Слайды и текст этой презентации

Слайд 1Интерполяция.
Метод с использование многочлена Лагранжа.
Пусть в n+1 узловой точке

x0, x1, x2, …, xn определены значения y0, y1, y2,

Слайд 2и тогда многочлен (1) примет вид:

Многочлен, который в n+1 узловой

точке будет принимать заданные значения, можно представить как сумму многочленов

Слайд 3Пример. По заданным точкам
Определить интерполяционный многочлен L(x).

L(x)=x2

Слайд 4function
yr=lagrange(x,y,xz)
n=length(x)
nz=length(xz)
i=1 шаг 1 до nz
k=1 шаг 1 до n
j=1 шаг

1 до n
yr(i)=0
pr=1
pr=pr(xz(i)-x(j))/(x(k)-x(j))
j~=k
yr(i)=yr(i)+pry(k)
End
Begin
End
x,y,xz
yz
yz=lagrange(x,y,xz)
lagrange(x,y,xz)

Слайд 5Метод наименьших квадратов
Пусть данные некоторого эксперимента представлены в виде таблицы

значений независимой переменной x и зависимой переменной y:
Требуется отыскать аналитическую

Слайд 6Функцию f(x,a0,a1,…,am) определим как полином степени m вида:
Надо найти такие

значения параметров, при которых квадратичный критерий рассогласования имел бы минимальное

Слайд 7или
Необходимые условия минимума критерия R имеют вид:

Слайд 8Полученную линейную относительно искомых параметров a0,a1,a2, систему уравнений запишем в

матричном виде:
где
Для удобства формирования матрицы коэффициентов
и столбца свободных

Слайд 9При аппроксимации полиномами высших порядков матрица

будет иметь вид:
Пример. Определить параметры зависимости вида
используя метод наименьших

Слайд 10

Слайд 11

Слайд 12Begin
End
m,n,x,y
a,dy,r
a=inv(F’F)F’y
i=1 шаг 1 до n
j=1 шаг 1 до m
F(i,j)=x(i)^(j-1)
yr=Fa; dy=y-yr
r=dy’*dy
close
plot(x,y,’ko’)
hold

on
plot(xt,yt,’k-’)

Обратная связь

Что такое TheSlide.ru?

Разделы презентаций

Приближение функции

Содержание

Слайды и текст этой презентации

Слайд 1Интерполяция.Метод с использование многочлена Лагранжа. Пусть в n+1 узловой точке

x0, x1, x2, …, xn определены значения y0, y1, y2,

Слайд 2и тогда многочлен (1) примет вид:Многочлен, который в n+1 узловой

точке будет принимать заданные значения, можно представить как сумму многочленов

Слайд 3Пример. По заданным точкамОпределить интерполяционный многочлен L(x).L(x)=x2

Слайд 4functionyr=lagrange(x,y,xz)n=length(x)nz=length(xz)i=1 шаг 1 до nzk=1 шаг 1 до nj=1 шаг

1 до nyr(i)=0pr=1pr=pr*(xz(i)-x(j))/(x(k)-x(j))j~=kyr(i)=yr(i)+pr*y(k)EndBeginEndx,y,xzyzyz=lagrange(x,y,xz)lagrange(x,y,xz)

Слайд 5Метод наименьших квадратовПусть данные некоторого эксперимента представлены в виде таблицы

значений независимой переменной x и зависимой переменной y:Требуется отыскать аналитическую

Слайд 6Функцию f(x,a0,a1,…,am) определим как полином степени m вида:Надо найти такие

значения параметров, при которых квадратичный критерий рассогласования имел бы минимальное

Слайд 7илиНеобходимые условия минимума критерия R имеют вид:

Слайд 8Полученную линейную относительно искомых параметров a0,a1,a2, систему уравнений запишем в

матричном виде: гдеДля удобства формирования матрицы коэффициентов и столбца свободных

Слайд 9При аппроксимации полиномами высших порядков матрица

будет иметь вид:Пример. Определить параметры зависимости вида используя метод наименьших

Слайд 10

Слайд 11

Слайд 12BeginEndm,n,x,ya,dy,ra=inv(F’*F)*F’*yi=1 шаг 1 до nj=1 шаг 1 до mF(i,j)=x(i)^(j-1)yr=F*a; dy=y-yrr=dy’*dycloseplot(x,y,’ko’)hold

on plot(xt,yt,’k-’)

Похожие презентации

Обратная связь

Что такое TheSlide.ru?

Слайд 1Интерполяция.
Метод с использование многочлена Лагранжа.
Пусть в n+1 узловой точке

Слайд 2и тогда многочлен (1) примет вид:

Многочлен, который в n+1 узловой

Слайд 3Пример. По заданным точкам
Определить интерполяционный многочлен L(x).

L(x)=x2

Слайд 4function
yr=lagrange(x,y,xz)
n=length(x)
nz=length(xz)
i=1 шаг 1 до nz
k=1 шаг 1 до n
j=1 шаг

1 до n
yr(i)=0
pr=1
pr=pr(xz(i)-x(j))/(x(k)-x(j))
j~=k
yr(i)=yr(i)+pry(k)
End
Begin
End
x,y,xz
yz
yz=lagrange(x,y,xz)
lagrange(x,y,xz)

Слайд 5Метод наименьших квадратов
Пусть данные некоторого эксперимента представлены в виде таблицы

значений независимой переменной x и зависимой переменной y:
Требуется отыскать аналитическую

Слайд 6Функцию f(x,a0,a1,…,am) определим как полином степени m вида:
Надо найти такие

Слайд 7или
Необходимые условия минимума критерия R имеют вид:

матричном виде:
где
Для удобства формирования матрицы коэффициентов
и столбца свободных

будет иметь вид:
Пример. Определить параметры зависимости вида
используя метод наименьших

Слайд 12Begin
End
m,n,x,y
a,dy,r
a=inv(F’F)F’y
i=1 шаг 1 до n
j=1 шаг 1 до m
F(i,j)=x(i)^(j-1)
yr=Fa; dy=y-yr
r=dy’*dy
close
plot(x,y,’ko’)
hold

on
plot(xt,yt,’k-’)