Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приложения определенного интеграла
Содержание
- 1. Приложения определенного интеграла
- 2. Вычисление площади плоских фигурПлощадь криволинейной трапеции, ограниченной
- 3. Слайд 3
- 4. Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x)
- 5. Если кривая y=f(x) на отрезке [a,b] –
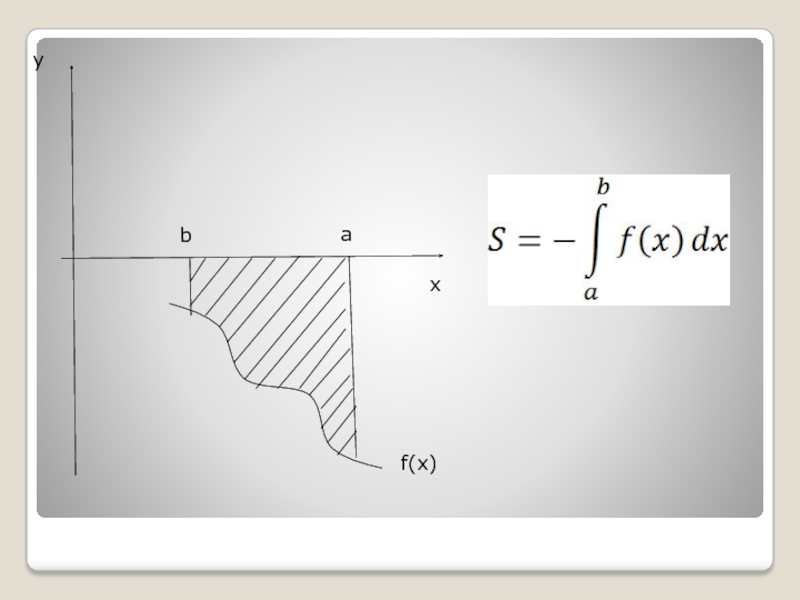
- 6. Если криволинейная трапеция, ограниченная кривой y=f(x) и
- 7. Если криволинейная трапеция, ограниченная кривой x=φ(y) и
- 8. Если фигура, ограниченная кривыми y1=f1(x) и y2=f2(x)
- 9. Задача 1: Найти площади фигуры, ограниченной линиями:y=x2 и y=2x-x2
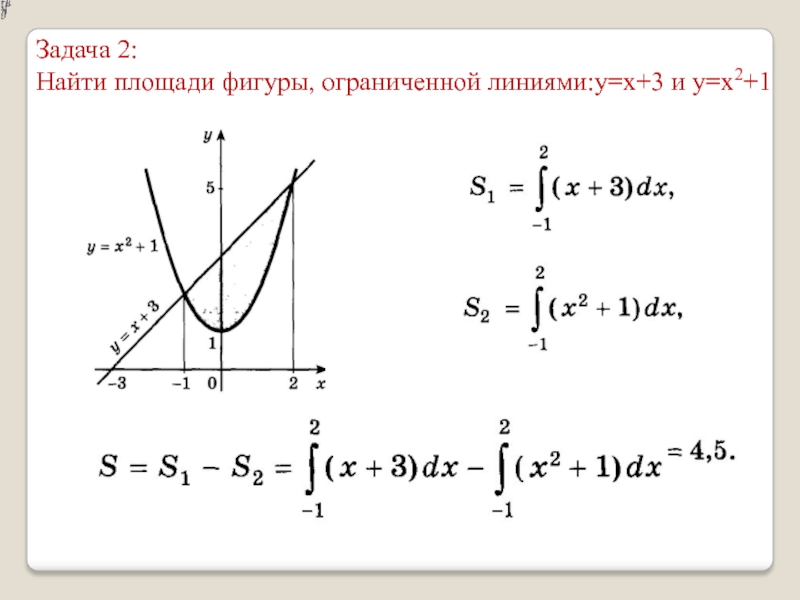
- 10. Задача 2: Найти площади фигуры, ограниченной линиями:y=x+3 и y=x2+1
- 11. Слайд 11
- 12. Скачать презентанцию
Вычисление площади плоских фигурПлощадь криволинейной трапеции, ограниченной кривой y=f(x), f(x)≥0, прямыми x=a и x=b и отрезком [a,b] оси Ox, вычисляется по формуле:
Слайды и текст этой презентации
Слайд 2Вычисление площади плоских фигур
Площадь криволинейной трапеции, ограниченной кривой y=f(x), f(x)≥0,
Слайд 4Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x) [f1(x) ≤ f2(x)]
и прямыми x=a и x=b, находится по формуле:
Слайд 5Если кривая y=f(x) на отрезке [a,b] – гладкая (т.е. производная
f’(x) непрерывна), то длина соответствующей дуги этой кривой находится по
формуле:Вычисление длины дуги плоской кривой
Слайд 6Если криволинейная трапеция, ограниченная кривой y=f(x) и прямыми y=0, x=a,
x=b, вращается вокруг оси Ox, то объем тела вращения вычисляется
по формуле:Вычисление объема тела вращения

![Приложения
определенного
интеграла Вычисление площади плоских фигурПлощадь криволинейной трапеции, ограниченной кривой y=f(x), f(x)≥0, прямыми Вычисление площади плоских фигурПлощадь криволинейной трапеции, ограниченной кривой y=f(x), f(x)≥0, прямыми x=a и x=b и отрезком [a,b]](/img/thumbs/5b568a7a1d329f363ed96c9d1361e7dd-800x.jpg)
![Приложения
определенного
интеграла Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x) [f1(x) ≤ f2(x)] и Площадь фигуры, ограниченной кривыми y=f1(x) и y=f2(x) [f1(x) ≤ f2(x)] и прямыми x=a и x=b, находится по](/img/thumbs/8bf16c3386fef7a5f1a5315ef7436d69-800x.jpg)
![Приложения
определенного
интеграла Если кривая y=f(x) на отрезке [a,b] – гладкая (т.е. производная f’(x) Если кривая y=f(x) на отрезке [a,b] – гладкая (т.е. производная f’(x) непрерывна), то длина соответствующей дуги этой](/img/thumbs/df5863673216802850bab86c91cbab4e-800x.jpg)


![Приложения
определенного
интеграла Если фигура, ограниченная кривыми y1=f1(x) и y2=f2(x) [0≤f1(x)≤f2(x)] и прямыми x=a, Если фигура, ограниченная кривыми y1=f1(x) и y2=f2(x) [0≤f1(x)≤f2(x)] и прямыми x=a, x=b, вращается вокруг оси Ox, то](/img/thumbs/c2afe4560de1f9dc30995822f3ad72d3-800x.jpg)