Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение Законов сохранения энергии
Содержание
- 1. Применение Законов сохранения энергии
- 2. Слайд 2
- 3. Слайд 3
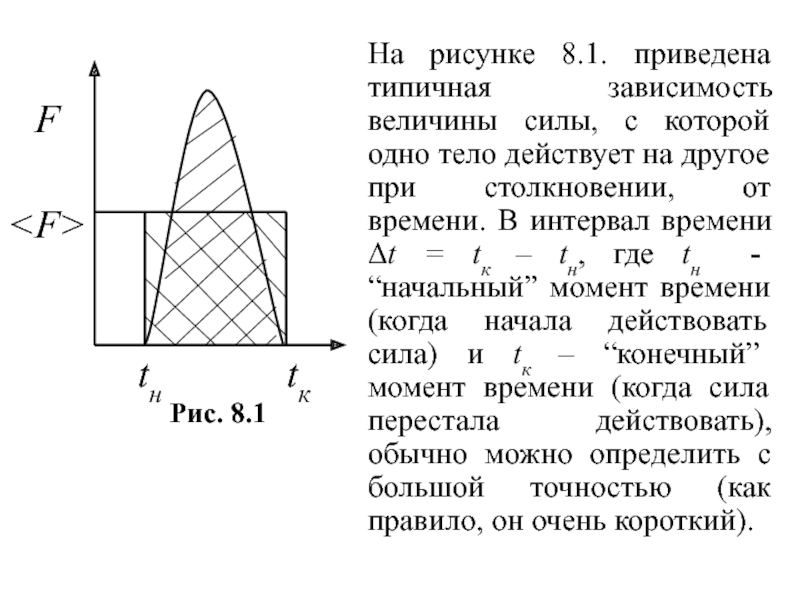
- 4. На рисунке 8.1. приведена типичная зависимость величины
- 5. Слайд 5
- 6. Интеграл от силы по времени в течение
- 7. Поскольку импульс силыравен площади под кривой, описывающей
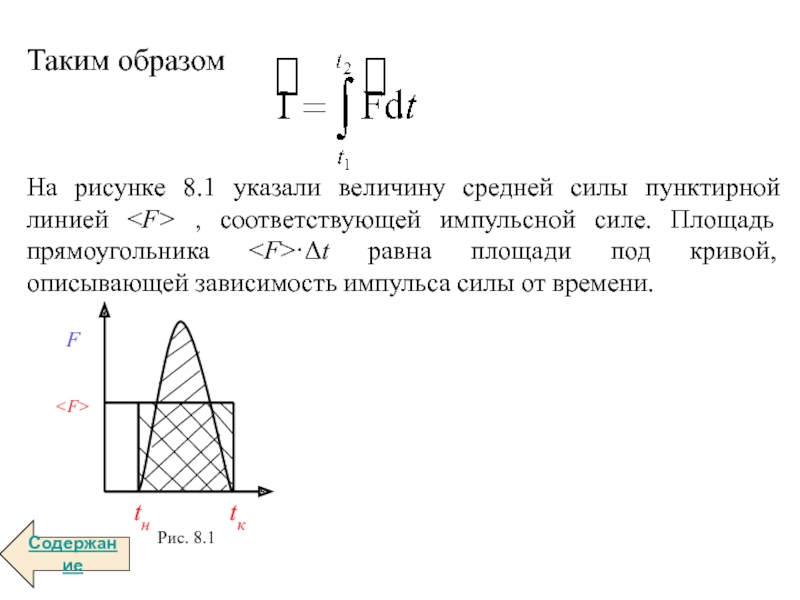
- 8. Таким образом На рисунке 8.1 указали величину
- 9. Задача. а) Вычислите импульс силы, который испытал
- 10. Применим теперь законы сохранения энергии и импульса
- 11. Отношение нормальных составляющих относительной скорости тел после
- 12. Слайд 12
- 13. 8.2.а). Абсолютно упругий удар – столкновение двух
- 14. Обозначим скорости частиц до удара через V1
- 15. Слайд 15
- 16. Разделив (8.6) на (8.4), получим
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Массивное тело практически остается в покое, тогда
- 21. д) V2=0, m1
- 22. Слайд 22
- 23. Слайд 23
- 24. Вследствие деформации происходит “потеря” кинетической энергии ,
- 25. Когда m2>>m1 (масса неподвижного тела очень большая),
- 26. Слайд 26
- 27. Скачать презентанцию
На рисунке 8.1. приведена типичная зависимость величины силы, с которой одно тело действует на другое при столкновении, от времени. В интервал времени Δt = tк – tн, где tн - “начальный”
Слайды и текст этой презентации
Слайд 1
8.1. Импульс силы
8.2. Удар абсолютно упругих и неупругих тел
8.3. Уравнение
движения системы с переменной массой
Слайд 4На рисунке 8.1. приведена типичная зависимость величины силы, с которой
одно тело действует на другое при столкновении, от времени. В
интервал времени Δt = tк – tн, где tн - “начальный” момент времени (когда начала действовать сила) и tк – “конечный” момент времени (когда сила перестала действовать), обычно можно определить с большой точностью (как правило, он очень короткий).Слайд 6Интеграл от силы по времени в течение которого она действует,
называется импульсом силы:
Таким образом, изменение импульса тела равно импульсу силы,
действующей на него:(8.1)
Единицы измерения импульса силы и импульса тела совпадают, т.е. в системе СИ мы имеем единицы кг⋅м/с (или Н/с).
Слайд 7Поскольку импульс силы
равен площади под кривой, описывающей зависимость величины силы
от t (рис. 8.1), формула (8.1) справедлива, только, если сила
есть равнодействующая всех сил, действующих на тело. Она справедлива для любой равнодействующей силы , причем импульсы pн и pк точно соответствуют моментам времени tн и tк. В некоторых случаях удобно использовать среднюю силу Fср, действующую во время столкновения. Она определяется как такая постоянная сила, которая действует в течение того же промежутка времени Δt=tк-tн, что и реальная сила, создает тот же импульс силы и, следовательно, тоже изменение импульса.Слайд 8Таким образом
На рисунке 8.1 указали величину средней силы пунктирной
линией , соответствующей импульсной силе. Площадь прямоугольника ·Δt равна
площади под кривой, описывающей зависимость импульса силы от времени.Содержание
Слайд 9Задача. а) Вычислите импульс силы, который испытал человек массой 70
кг, приземлившись на твёрдую землю после прыжка с высоты 5,0
м. Найдите при этом среднюю силу, действовавшую на ноги человека, если он приземлился б) на прямые ноги и в) на согнутых ногах. Предположим, что в случае п. б) центр масс тела во время удара о землю переместился на 1,0 см, а в случае п. в) на 50 см.Примечание: Предел прочности (предельные напряжения) кости (конечности) на растяжение – 130·106 Н/м2, на сжатие – 170·106 Н/м2
Слайд 10Применим теперь законы сохранения энергии и импульса к лобовому упругому
и неупругому удару. Тела во время удара претерпевают деформацию. Сущность
удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел на короткое время преобразуется в энергию упругой деформации. Во время удара происходит перераспределение энергии между соударяющимися телами. Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего значения. Это объясняется тем, что нет идеально упругих тел и идеально гладких поверхностей.Слайд 11Отношение нормальных составляющих относительной скорости тел после и до удара
называется коэффициентом восстановления k:
Если для сталкивающихся тел k = 0,
то такие тела называются абсолютно неупругими, если k = 1 – абсолютно упругими. На практике для тел 0 < k < 1 (например, для стальных шаров k ≈ 0,56, для шаров из слоновой кости k ≈ 0,89, для свинца k ≈ 0). Однако в некоторых случаях тела можно рассматривать с большой степенью точности как абсолютно упругие, либо как абсолютно неупругие.Слайд 138.2.а). Абсолютно упругий удар – столкновение двух тел, в результате
которого в обоих взаимодействующих телах не остается никаких деформаций и
кинетическая энергия, которой обладали тела до удара, после удара снова превращается в кинетическую энергию (это идеальный случай). Для абсолютно упругого удара выполняется закон сохранения импульса и закон сохранения кинетической энергии.Слайд 14Обозначим скорости частиц до удара через V1 и V2, а
после удара и . При любом значении
V > 0 частица движется вправо (координата х возрастает), в то время как при V < 0 частица движется влево и координата х уменьшается. Напоминаю, мы рассматриваем центральный удар.Слайд 16Разделив (8.6) на (8.4), получим
или (8.7)
Итак, мы получили, что
относительная скорость двух частиц после столкновения в точности равна их относительной скорости до столкновения.
!Это верно для любого лобового удара, независимо от того, какие массы имеют частицы!
Слайд 20Массивное тело практически остается в покое, тогда как очень легкое
тело отскакивает практически с той же по величине (но противоположно
направленной) скоростью.г) V2=0, m1>m2. Первый шар продолжает двигаться в том же направлении, как и до удара, но с меньшей скоростью . Скорость второго шара после удара больше, чем скорость первого после удара .
Слайд 21д) V2=0, m1
отскакивает обратно. Второй шар движется в ту же сторону, в
которую двигался первый шар до удара, но с меньшей скоростью, т.е. .Слайд 24Вследствие деформации происходит “потеря” кинетической энергии , перешедшей в тепловую
или другие формы энергии. Эту “потерю” можно определить по разности
кинетических энергий до и после удара:Используя (8.9), получаем
Если ударяемое тело было первоначально неподвижно (V2=0), то
,
Слайд 25Когда m2>>m1 (масса неподвижного тела очень большая), то V
почти вся кинетическая энергия при ударе переходит в другие формы
энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка.Когда m1>>m2, тогда V≈V1 и практически вся энергия затрачивается на возможно большее перемещение, а не на остаточную деформацию (пример, молоток - гвоздь).
Абсолютно неупругий удар – пример того, как происходит “потеря” механической энергии под действием диссипативных сил.
Содержание