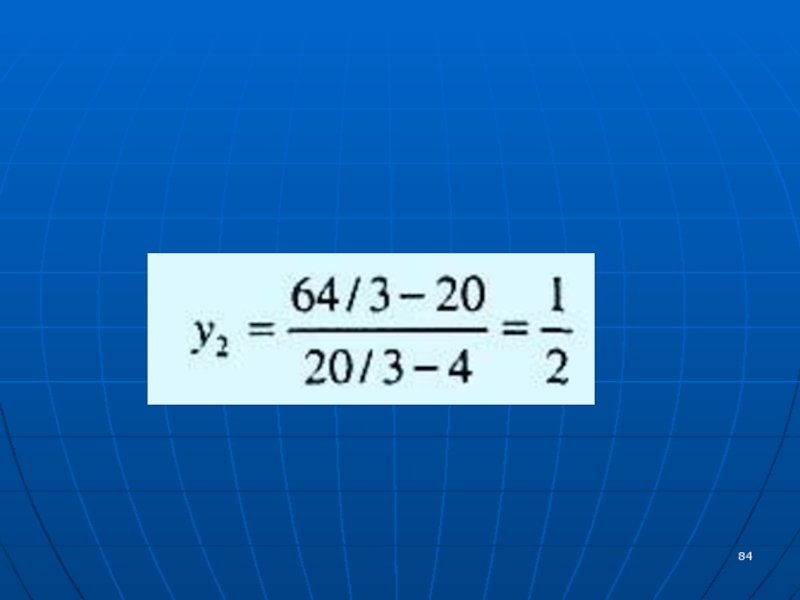Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Пример задачи линейного программирования
Содержание
- 1. Пример задачи линейного программирования
- 2. Слайд 2
- 3. Отдел маркетинга компании ограничил ежедневное производство краски
- 4. Задача (модель) линейного программирования, как и любая
- 5. В нашем примере необходимо определить ежедневные объемы
- 6. Используя эти переменные, далее строим целевую функцию.
- 7. ОграниченияИспользуемый объем сырья Ml = 6x1 +
- 8. Существует еще два ограничения по спросу на
- 9. Второе можно сформулировать так: разность между ежедневными
- 10. Окончательно задача будет записана следующим образом: Максимизировать
- 11. Графический метод решения задач линейного программирования. Графически
- 12. Формализация для двух переменныхцелевая функция: Zmax =
- 13. Этап 1. Построение пространства допустимых решений.Сначала проведем
- 14. Теперь рассмотрим, как графически интерпретируются неравенства. Каждое
- 15. Например, эта точка удовлетворяет первому неравенству 6х1
- 16. Слайд 16
- 17. Этап 2. Нахождение оптимального решения. Точки пространства
- 18. Нахождение оптимального решения требует определения направления возрастания
- 19. Слайд 19
- 20. Целевая функция может возрастать до тех пор,
- 21. 6x1 + 4x2 = 24, x1 +
- 22. Применение метода графического решения задач линейного программирования
- 23. Слайд 23
- 24. Диетологи требуют, чтобы в пищевой добавке было
- 25. Целевая функция равна обшей стоимости пищевой добавки,
- 26. Общее количество белка в смеси, состоящей из
- 27. В последних двух неравенствах переменные x1 и
- 28. Слайд 28
- 29. Оптимальное решение находится на пересечении прямых x1
- 30. Понятие дополнительной переменной в задачах линейного программирования. Анализ чувствительности решений.
- 31. Остаточные и избыточные переменные В ранее рассмотренных
- 32. Пример из задачи «Русские краски»Максимизировать z =
- 33. Введем два типа дополнительных неотрицательных переменных (назовем
- 34. Остаточная переменная. Неравенства типа "≤" обычно можно
- 35. В примере с компанией "Русские краски" неравенство
- 36. Избыточная переменная. Неравенство типа "≥" показывает, что
- 37. В модели "диеты" неравенство x1 + х2
- 38. Свободная переменная. В приведенных выше примерах условие
- 39. Ресторан быстрого обслуживания Ресторан быстрого обслуживания торгует
- 40. Ресторан имеет доход 20 руб. от одной
- 41. РешениеСначала рассмотрим ограничения. Обозначим через х1 и
- 42. Так как мы не знаем, какое из
- 43. Далее построим целевую функцию. Ресторан хочет максимизировать
- 44. Для того чтобы раскрыть "двойственную" природу переменной
- 45. Итак, теперь ограничение можно записать в виде
- 46. Представление задачи линейного программирования в канонической форме.
- 47. Любую задачу линейного программирования можно свести к
- 48. Правило приведения задачи линейного программирования к каноническому
- 49. если некоторая переменная xj не имеет ограничений
- 50. Пример приведения к канонической форме min L
- 51. Введем в каждое уравнение системы ограничений выравнивающие
- 52. 2x2 - x3 + x4 = 5;
- 53. В канонической форме записи задач линейного программирования
- 54. Подставляя данное выражение в систему ограничений и
- 55. Lmin = 2x1' + x2 - x3
- 56. Графический анализ чувствительности модели задачи линейного программирования.
- 57. Анализ моделей на чувствительность — это процесс,
- 58. Рассмотрим два случая: изменение коэффициентов целевой функции.изменение значений констант в правой части неравенств ограничений.
- 59. Анализ модели на чувствительность к изменению значений
- 60. Графический способ решения задачи ЛП показывает, что
- 61. Задача анализа чувствительности и состоит в получении
- 62. Пример Применим процедуру анализа чувствительности к модели
- 63. Слайд 63
- 64. При изменении коэффициентов целевой функции z =
- 65. Алгебраически это можно записать следующим образом:или
- 66. В первой системе неравенств условие c1 0
- 67. Из рис. видно, что интервал оптимальности данной
- 68. Итак, если коэффициенты c1 и c2 удовлетворяют
- 69. Приведенные выше неравенства можно использовать при определении
- 70. Подставим с2=4, получим 2 ≤ с1 ≤
- 71. получаем интервал оптимальности для коэффициента с2: 10/3 ≤ с2 ≤ 10.
- 72. Изменение значений констант в правой части неравенств
- 73. Такой анализ задачи ЛП предлагает простую меру
- 74. В модели для компании "Русские краски" первые
- 75. Слайд 75
- 76. При изменении уровня доступности материала M1 (увеличение
- 77. Аналогично количество сырья, соответствующего точке G =
- 78. Это означает, что текущий уровень ресурса M1
- 79. Слайд 79
- 80. Если точка С совпадает с точкой D
- 81. Этот результат показывает, что изменение количества ресурса
- 82. Слайд 82
- 83. Видно, что интервал осуществимости для ресурса М2
- 84. Слайд 84
- 85. Скачать презентанцию
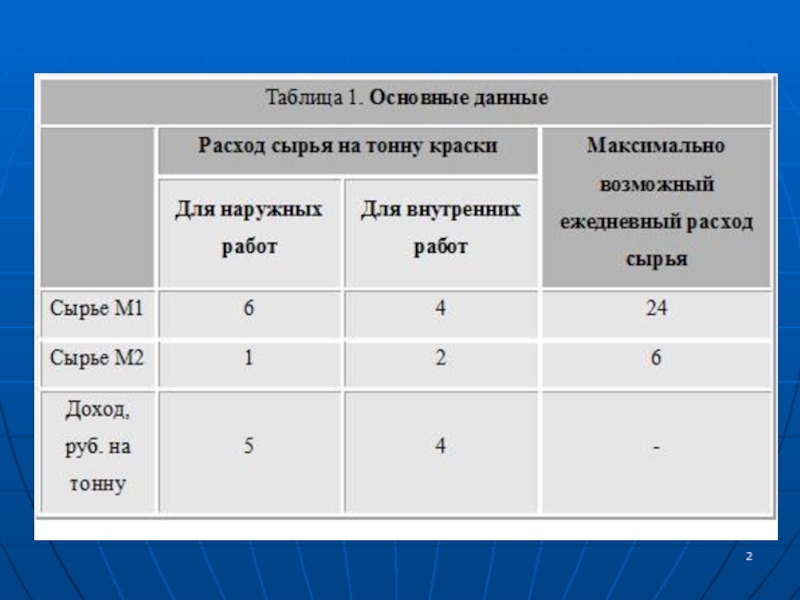
Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ до 2 т (из-за отсутствия надлежащего спроса), а также поставил условие, чтобы ежедневное производство краски для внутренних работ не превышало более
Слайды и текст этой презентации
Слайд 3Отдел маркетинга компании ограничил ежедневное производство краски для внутренних работ
до 2 т (из-за отсутствия надлежащего спроса), а также поставил
условие, чтобы ежедневное производство краски для внутренних работ не превышало более чем на тонну аналогичный показатель производства краски для внешних работ. Компания хочет определить оптимальное (наилучшее) соотношение между видами выпускаемой продукции для максимизации общего ежедневного дохода.Слайд 4Задача (модель) линейного программирования, как и любая задача исследования операций,
включает три основных элемента.
Переменные, которые следует определить.
Целевая функция,
подлежащая оптимизации. Ограничения, которым должны удовлетворять переменные.
Слайд 5
В нашем примере необходимо определить ежедневные объемы производства краски для
внутренних и наружных работ. Обозначим эти объемы как переменные модели:
x1 — ежедневный объем производства краски для наружных работ;
х2 — ежедневный объем производства краски для внутренних работ.
Слайд 6Используя эти переменные, далее строим целевую функцию. Логично предположить, что
целевая функция, как суммарный ежедневный доход, должна возрастать при увеличении
ежедневных объемов производства красок. Обозначим эту функцию через z (она измеряется в тысячах руб) и положим, что Z = 5x1 + 4x2.В соответствии с целями компании получаем задачу:
Максимизировать Z = 5x1 + 4x2.
Слайд 7Ограничения
Используемый объем сырья Ml = 6x1 + 4х2 (т)
Используемый
объем сырья М2 = 1x1 + 2х2 (т)
Так как
ежедневный расход сырья Ml и М2 ограничен соответственно 24 и 6 тоннами, получаем следующие ограничения. 6x1 + 4х2 ≤ 24 (сырье Ml) x1 + 2x2 ≤ 6 (сырье М2) Слайд 8Существует еще два ограничения по спросу на готовую продукцию: (1)
максимальный ежедневный объем производства краски для внутренних работ не должен
превышать 2 т и (2) ежедневный объем производства краски для внутренних работ не должен превышать ежедневный объем производства краски для наружных работ более чем на одну тонну. Первое ограничение простое и записывается как х2 ≤ 2.Слайд 9Второе можно сформулировать так: разность между ежедневными объемами производства красок
для внутренних и наружных работ не должна превышать одной тонны,
т.е. х2 – x1 ≤ 1.Еще одно неявное ограничение состоит в том, что переменные x1 и х2 должны быть неотрицательными. Таким образом, к сформулированным выше ограничениям необходимо добавить условие неотрицательности переменных.
Слайд 10Окончательно задача будет записана следующим образом: Максимизировать z = 5х1 +
4х2 при выполнении ограничений 6х1 + 4х2 ≤ 24, x1 +
2х2 ≤ 6, -x1 + 2x2 ≤1 х2 ≤ 2, х1 ≥ 0, х2 ≥ 0.Слайд 11Графический метод решения задач линейного программирования.
Графически способ решения задач
линейного программирования целесообразно использовать:
Для решения задач с двумя переменными,
когда ограничения выражены неравенствами; Решения задач со многими переменными при условии, что в их канонической записи содержится не более двух свободных переменных.
Слайд 12Формализация для двух переменных
целевая функция: Zmax = c1x1 + c2x2
(1)
Ограничения:x1 ≥ 0, x2 ≥ 0.
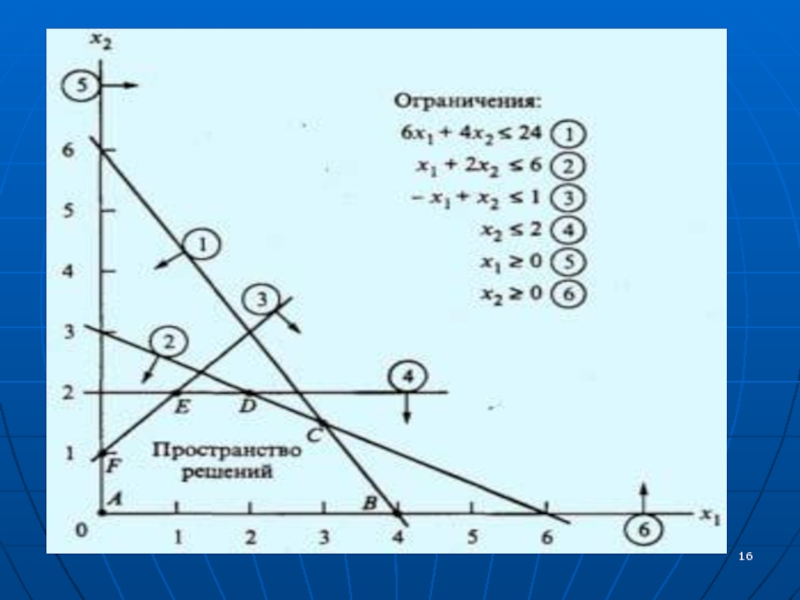
Слайд 13Этап 1. Построение пространства допустимых решений.
Сначала проведем оси: на горизонтальной
будут указываться значения переменной х1, а на вертикальной — х2.
Далее рассмотрим условие неотрицательности переменных: х1 ≥ 0 и х2 ≥ 0. Эти два ограничения показывают, что пространство допустимых решений будет лежать в первом квадранте.Чтобы учесть оставшиеся ограничения заменим неравенства на равенства, в результате чего получим уравнения прямых, а затем на плоскости проведем эти прямые.
Слайд 14Теперь рассмотрим, как графически интерпретируются неравенства. Каждое неравенство делит плоскость
(х1 , х2) на два полупространства, которые располагаются по обе
стороны прямой, которая соответствует данному неравенству. Точки плоскости, расположенные по одну сторону прямой, удовлетворяют неравенству (допустимое полупространство), а точки, лежащие по другую сторону, — нет. "Тестовой" точкой, проверяющей, точки какого полупространства удовлетворяют неравенству, а какого — нет, может служить точка (0, 0).Слайд 15Например, эта точка удовлетворяет первому неравенству 6х1 + 4х2
24 (здесь 6*0 + 4*0 = 0 < 24). Это
означает, что точки полупространства, содержащего начальную точку (0,0), удовлетворяют этому неравенству. На рис. на следующем слайде допустимые полупространства показаны стрелочками.Слайд 17Этап 2. Нахождение оптимального решения.
Точки пространства допустимых решений, показанного
на рис., удовлетворяют одновременно всем ограничениям. Это пространство ограничено отрезками
прямых, которые соединяются в угловых точках А, В, С, D, Е и F. Любая точка, расположенная внутри или на границе области, ограниченной ломаной ABCDEF, является допустимым решением, т.е. удовлетворяет всем ограничениям.Слайд 18Нахождение оптимального решения требует определения направления возрастания целевой функции z
= 5х1 + 4х2. Мы можем приравнять z к нескольким
возрастающим значениям, например 10 и 15. Эти значения, подставленные вместо z в выражение целевой функции, порождают уравнения прямых; для значений 10 и 15 получаем уравнения прямых 5х1 + 4х2= 10 и 5х1 + 4х2= 15. На рис. эти прямые показаны штриховыми линиями, а направление возрастания целевой функции — толстой стрелкой.Слайд 20Целевая функция может возрастать до тех пор, пока прямые, соответствующие
возрастающим значениям этой функции, пересекают область допустимых решений. Точка пересечения
области допустимых решений и прямой, соответствующей максимально возможному значению целевой функции, и будет точкой оптимума.На рис. 2 видно, что оптимальное решение соответствует точке С. Эта точка является местом пересечения прямых (1) и (2), поэтому ее координаты x1 и х2 находятся как решение системы уравнений, задающих эти прямые:
Слайд 216x1 + 4x2 = 24,
x1 + 2x2 = 6
Решением
этой системы будет х1 = 3 и х2 = 1.5,
при этом значение целевой функции равно z = 21. Полученное решение означает, что для компании "Русские краски" оптимальным выбором будет ежедневное производство 3 т краски для наружных работ и 1.5 т — для внутренних работ с ежедневным доходом в 21000.Слайд 22Применение метода графического решения задач линейного программирования для случая минимизации
целевой функции.
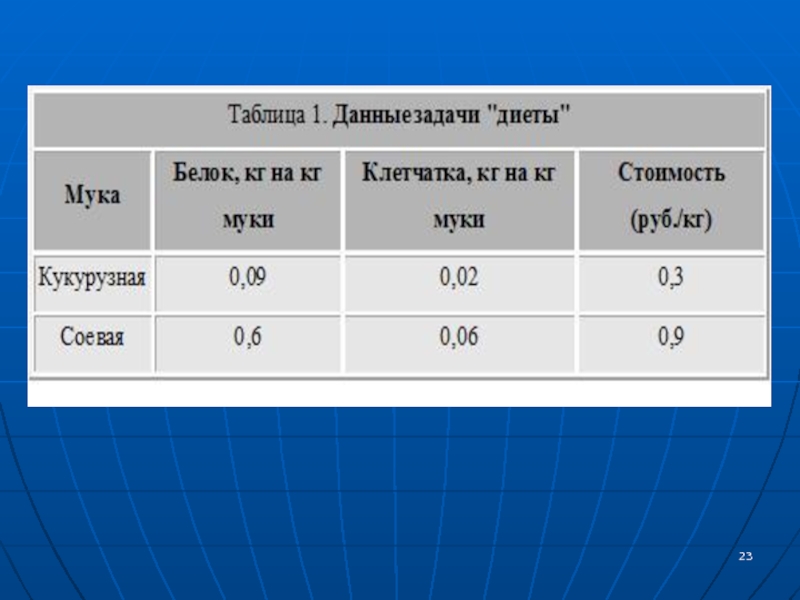
Фармацевтическая фирма ежедневно производит не менее 800 кг
некой пищевой добавки, которая состоит из смеси кукурузной и соевой муки, состав которой представлен в следующей таблице. Слайд 24Диетологи требуют, чтобы в пищевой добавке было не менее 30%
белка и не более 5% клетчатки. Фирма хочет определить рецептуру
смеси наименьшей стоимости с учетом требований диетологов.Поскольку пищевая добавка состоит только из кукурузной и соевой муки, переменными для этой задачи, очевидно, будут x1 — количество (в кг) кукурузной муки, используемой в дневном производстве пищевой добавки; х2 — количество (в кг) соевой муки, используемой в дневном производстве пищевой добавки.
Слайд 25Целевая функция равна обшей стоимости пищевой добавки, производимой за один
день, и должна быть минимальной. В данном случае это можно
записать следующим образом:Минимизировать z = 0,3 x1+ 0,9x2.
Ограничения модели должны отражать производственные требования и рекомендации диетологов. Фирма должна выпускать не менее 800 кг смеси в день.Соответствующее ограничение будет записано следующим образом: x1+ x2 ≥ 800.
Слайд 26Общее количество белка в смеси, состоящей из х1 кг кукурузной
муки и х2 кг соевой муки, равно 0.09x1 + 0.6х2
(кг). Это количество должно составлять не менее 30% от общего объема смеси х1 + х2. Отсюда получаем следующее неравенство0.09х1 + 0.6x2 ≥ 0.3(x1 + х2).
Аналогично строится ограничение для клетчатки:
0.02x1 + 0.06х2 ≤ 0.05(х1 + х2).
Слайд 27В последних двух неравенствах переменные x1 и х2 надо перенести
из правых частей неравенств в левые. Окончательно модель примет следующий
вид:Минимизировать z = 0.3x1 + 0.9x2 при ограничениях x1 + x2 ≥ 800, 0.21х1 - 0.3x2 ≤ 0, 0.03x1 - 0.01x2 ≥ 0, x1, x2 ≥ 0.
На рис. показано графическое решение этой задачи.
Слайд 29Оптимальное решение находится на пересечении прямых x1 + х2 =
800 и 0.21x1 - 0.30x2 = 0, откуда получаем х1
= 470.59 (кг) и х2 = 329.41 (кг). При этих значениях переменных минимальная стоимость производимой ежедневно пищевой добавки составляет z = 0.3 * 470.59 + 0.9 * 329.41 = 437.65 руб.Слайд 30Понятие дополнительной переменной в задачах линейного программирования.
Анализ чувствительности решений.
Слайд 31Остаточные и избыточные
переменные
В ранее рассмотренных примерах мы использовали неравенства
типа "меньше или равно" и "больше или равно". В этих
примерах также предполагалась не отрицательность всех переменных.Слайд 32Пример из задачи «Русские краски»
Максимизировать z = 5х1 + 4х2
при выполнении ограничений 6х1 + 4х2 ≤ 24, x1 + 2х2
≤ 6, -x1 + 2x2 ≤1 х2 ≤ 2, х1 ≥ 0, х2 ≥ 0.Слайд 33Введем два типа дополнительных неотрицательных переменных (назовем их остаточными и
избыточными, которые связаны с неравенствами, типа "≤" и "≥" соответственно.
Введем также понятие свободной переменной, которая может принимать как положительные, так и отрицательные значения (и, конечно, значение 0).Слайд 34Остаточная переменная.
Неравенства типа "≤" обычно можно интерпретировать как ограничения
на использование некоторых ресурсов (представленных в левой части неравенств переменными
модели). В такой интерпретации остаточная переменная показывает количество неиспользованных ресурсов.Слайд 35В примере с компанией "Русские краски" неравенство 6x1 + 4х2
≤ 24 связано с использованием сырья M1.
Это неравенство эквивалентно
равенству 6x1 + 4х2 + s1 = 24, где s1 ≥ 0. Здесь остаточная переменная s1 (= 24 - 6x1 - 4х2) равна неиспользуемому количеству сырья M1. Слайд 36Избыточная переменная.
Неравенство типа "≥" показывает, что "что-то" должно быть
не меньше определенной величины. Избыточная переменная определяет превышение значения левой
части неравенства над этой величиной.Пример из «Диеты» из прошлой лекции:
Слайд 37В модели "диеты" неравенство x1 + х2 ≥ 800 показывает,
что суточное производство пищевой добавки не должно быть меньше 800
кг. Математически это неравенство эквивалентно равенству x1 + х2 – S1 = 800, где S1 > 0. Положительное значение избыточной переменной S1 показывает превышение суточного производства добавки над минимальным значением в 800 кг.Слайд 38Свободная переменная.
В приведенных выше примерах условие не отрицательности переменных
является естественным. Но, конечно, возможны ситуации, когда переменные могут принимать
любые действительные значения. Такая ситуация показана в следующем примере.Слайд 39Ресторан быстрого обслуживания
Ресторан быстрого обслуживания торгует порционными мясными пирогами
и чизбургерами. На порцию мясного пирога идет четверть кг мяса,
а на чизбургер — только 0.2 кг. В начале рабочего дня в ресторане имеется 200 кг мяса, можно еще прикупить мясо в течение дня, но уже с наценкой в 25 руб. Мясо, оставшееся в конце рабочего дня, жертвуется благотворительной организации.Слайд 40Ресторан имеет доход 20 руб. от одной порции мясного пирога
и 15 руб. — от одного чизбургера. Как и многие
другие, этот ресторан не может продать в день более 900 бутербродов. Какова должна быть доля каждого из бутербродов (т.е. сколько порций мясного пирога и сколько чизбургеров) в ежедневном производстве ресторана, чтобы максимизировать его доход?Слайд 41Решение
Сначала рассмотрим ограничения. Обозначим через х1 и х2 соответственно количество
порций мясного пирога и чизбургеров, производимых рестораном. Для их производства
ресторан может ограничиться 200 кг мяса или может прикупить еще. В первом случае получаем ограничение в виде неравенства 0.25x1 + 0.2x2 ≤ 200, а во втором — 0.25x1 + 0.2x2 ≥ 200. Естественно, выбор одного из этих неравенств будет существенно влиять на возможное оптимальное решение.Слайд 42Так как мы не знаем, какое из них необходимо, логично
заменить их одним равенством 0.25x1 + 0.2x2 + x3 =
200, где x3 — свободная переменная. Фактически свободная переменная x3 в данной ситуации одновременно играет роль как остаточной, так и избыточной переменных.Слайд 43Далее построим целевую функцию. Ресторан хочет максимизировать свой доход. Очевидно,
что для максимизации дохода желательно как можно больше продавать своей
продукции, но для этого необходимы дополнительные закупки мяса. В этом случае переменная x3 должна быть отрицательной, т.е. должна играть роль избыточной переменной.Слайд 44Для того чтобы раскрыть "двойственную" природу переменной x3, используем стандартный
математический прием, а именно представим ее в следующем виде
x3
= x3+ - x3-, где x3+, x3- ≥ 0. Если x3+ > 0 и х3- = 0, тогда переменная x3 играет роль остаточной.
Если, напротив, x3+ = 0 и х3- > 0, тогда переменная x3 выступает в роли избыточной.
Слайд 45Итак, теперь ограничение можно записать в виде равенства 0.25х1 +
0.2х2 + x3+ - х3- = 200. Целевая функция получает
следующее выражение.Максимизировать z = 0.20x1 + 0.15х2 - 0.25 х3-
Слайд 46Представление задачи линейного программирования в канонической форме.
Если математическая модель
задачи линейного программирования имеет вид:
то говорят, что задача представлена
в канонической форме. Слайд 47Любую задачу линейного программирования можно свести к задаче линейного программирования
в канонической форме. Для этого в общем случае нужно уметь
сводить задачу максимизации к задаче минимизации; переходить от ограничений неравенств к ограничениям равенств и заменять переменные, которые не подчиняются условию неотрицательности. Максимизация некоторой функции эквивалента минимизации той же функции, взятой с противоположным знаком, и наоборот.Слайд 48Правило приведения задачи линейного программирования к каноническому виду
если в
исходной задаче требуется определить максимум линейной функции, то следует изменить
знак и искать минимум этой функции;если в ограничениях правая часть отрицательна, то следует умножить это ограничение на -1;
если среди ограничений имеются неравенства, то путем введения дополнительных неотрицательных переменных они преобразуются в равенства;
Слайд 49если некоторая переменная xj не имеет ограничений по знаку, то
она заменяется (в целевой функции и во всех ограничениях) разностью
между двумя новыми неотрицательными переменными: x3 = x3+ - x3-, где x3+, x3- ≥ 0.Слайд 50Пример приведения к канонической форме
min L = 2x1 +
x2 - x3; 2x2 - x3 ≤ 5; x1 + x2 -
x3 ≥ -1; 2x1 - x2 ≤ -3; x1 ≤ 0; x2 ≥ 0; x3 ≥ 0.Слайд 51Введем в каждое уравнение системы ограничений выравнивающие переменные x4, x5,
x6. Система запишется в виде равенств, причем в первое и
третье уравнения системы ограничений переменные x4, x6 вводятся в левую часть со знаком "+", а во второе уравнение переменная x5 вводится со знаком "-".Слайд 522x2 - x3 + x4 = 5; x1 + x2 -
x3 - x5 = -1; 2x1 - x2 + x6 =
-3; x4 ≥ 0; x5 ≥ 0; x6 ≥ 0.Свободные члены в канонической форме должны быть положительными, для этого два последних уравнения умножим на -1:
2x2 - x3 + x4 = 5; -x1 - x2 + x3 + x5 = 1; -2x1 + x2 - x6 = 3.
Слайд 53В канонической форме записи задач линейного программирования все переменные, входящие
в систему ограничений, должны быть отрицательными. Допустим, что x1 =
x1' - x7, где x1' ≥ 0, x7 ≥ 0.Слайд 54Подставляя данное выражение в систему ограничений и целевую функцию и,
записывая переменные в порядке возрастания индекса, получим задачу линейного программирования,
представленную в канонической форме:Слайд 55Lmin = 2x1' + x2 - x3 - 2x7; 2x2 -
x3 + x4 = 5; -x1' - x2 + x3 +
x5 + x7 = 1; -2x1' + x2 - x6 + 2x7 = 3; x1' ≥ 0; xi ≥ 0, i=2, 3, 4, 5, 6, 7.Слайд 56Графический анализ чувствительности модели задачи линейного программирования.
Модель линейного программирования
является как бы "моментальным снимком" реальной ситуации, когда параметры модели
(коэффициенты целевой функции и неравенств ограничений) предполагаются неизменными. Естественным стремлением является изучить влияние изменения параметров модели на полученное оптимальное решение задачи ЛП. Такое исследование называется анализом чувствительности.Слайд 57Анализ моделей на чувствительность — это процесс, реализуемый после получения
оптимального решения. В рамках такого анализа выявляется чувствительность оптимального решения
к определенным изменениям исходной модели.Например, в задаче об ассортименте продукции может представлять интерес вопрос о том, как повлияет на оптимальное решение увеличение и уменьшение спроса на продукцию или запасов исходного сырья.
Слайд 58Рассмотрим два случая:
изменение коэффициентов целевой функции.
изменение значений констант в
правой части неравенств ограничений.
Слайд 59Анализ модели на чувствительность к изменению значений коэффициентов целевой функции.
В общем виде целевую функцию задачи ЛП с двумя переменными
можно записать следующим образом: z = с1x1 + с2х2 Изменение значений коэффициентов c1 и c2 приводит к изменению угла наклона прямой z.
Слайд 60Графический способ решения задачи ЛП показывает, что это может привести
к изменению оптимального решения: оно будет достигаться в другой угловой
точке пространства решений. Вместе с тем, очевидно, существуют интервалы изменения коэффициентов c1 и c2, когда текущее оптимальное решение сохраняется.Слайд 61Задача анализа чувствительности и состоит в получении такой информации. В
частности, представляет интерес определение интервала оптимальности для отношения c1/c2 (или,
что то же самое, для c2/c1); если значение отношения c1/c2 не выходит за пределы этого интервала, то оптимальное решение в данной модели сохраняется неизменным.Слайд 62Пример
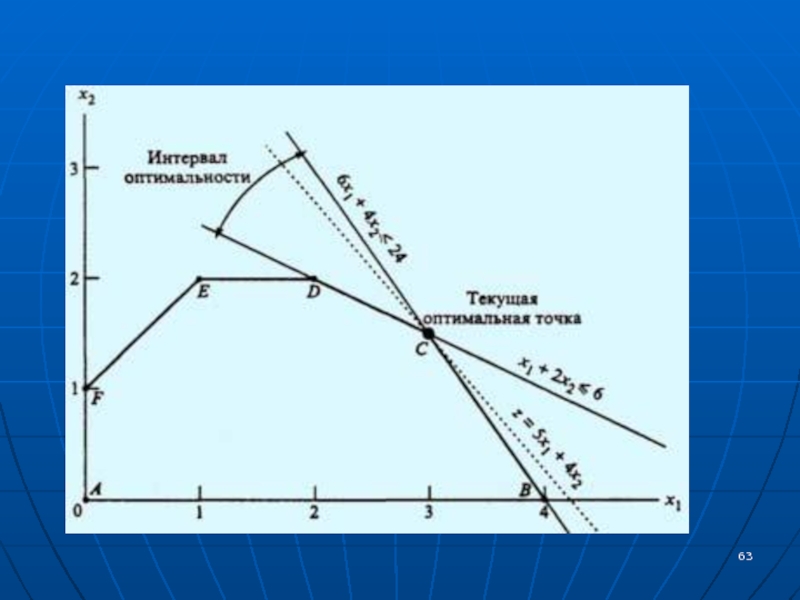
Применим процедуру анализа чувствительности к модели для компании "Русские
краски". На рис. на следущем слайде будет видно, что функция
z = 5х1 + 4х2 достигает максимального значения в угловой точке С.Слайд 64При изменении коэффициентов целевой функции z = с1x1 + с2х2
точка С останется точкой оптимального решения до тех пор, пока
угол наклона линии z будет лежать между углами наклона двух прямых, пересечением которых является точка С. Этими прямыми являются 6х1 + 4х2 = 24 (ограничение на сырье M1) и х1 + 2х2 = 6 (ограничение на сырье М2).Слайд 66В первой системе неравенств условие c1 0 означает, что
прямая, соответствующая целевой функции, не может быть горизонтальной.
Аналогичное условие
в следующей системе неравенств означает, что эта же прямая не может быть вертикальной. Слайд 67Из рис. видно, что интервал оптимальности данной задачи (он определяется
двумя прямыми, пересекающимися в точке С) не разрешает целевой функции
быть ни горизонтальной, ни вертикальной прямой. Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности в нашем примере.Слайд 68Итак, если коэффициенты c1 и c2 удовлетворяют приведенным выше неравенствам,
оптимальное решение будет достигаться в точке С.
Отметим, если прямая
z = с1x1 + с2х2 совпадет с прямой х1 + 2х2 = 6, то оптимальным решением будет любая точка отрезка CD. Аналогично, если прямая, соответствующая целевой функции, совпадет с прямой 6x1 + 4х2 = 24, тогда любая точка отрезка ВС будет оптимальным решением. Однако заметим, что в обоих случаях точка С остается точкой оптимального решения.
Слайд 69Приведенные выше неравенства можно использовать при определении интервала оптимальности для
какого-либо одного коэффициента целевой функции, если предположить, что другой коэффициент
остается неизменным. Например, если в нашей модели зафиксировано значение коэффициента с2 (пусть с2 = 4), тогда интервал оптимальности для коэффициента с1 получаем из неравенствСлайд 70Подставим с2=4, получим 2 ≤ с1 ≤ 6
Аналогично, если
зафиксировать значение коэффициента с1 (например, с1 = 5), тогда из
неравенствСлайд 72Изменение значений констант в правой части неравенств ограничений.
Во многих моделях
линейного программирования ограничения трактуются как условия ограниченности ресурсов. В таких
ограничениях правая часть неравенств является верхней границей количества доступных ресурсов. Рассмотрим чувствительность оптимального решения к изменению ограничений, накладываемых на ресурсы.Слайд 73Такой анализ задачи ЛП предлагает простую меру чувствительности решения, называемую
стоимостью единицы ресурса; при изменении количества доступных ресурсов (на единицу)
значение целевой функции в оптимальном решении изменится на стоимость единицы ресурса.Проиллюстрируем этот вид анализа задачи ЛП на следующем примере.
Слайд 74В модели для компании "Русские краски" первые два неравенства представляют
собой ограничения на использование сырья M1 и М2 соответственно. Определим
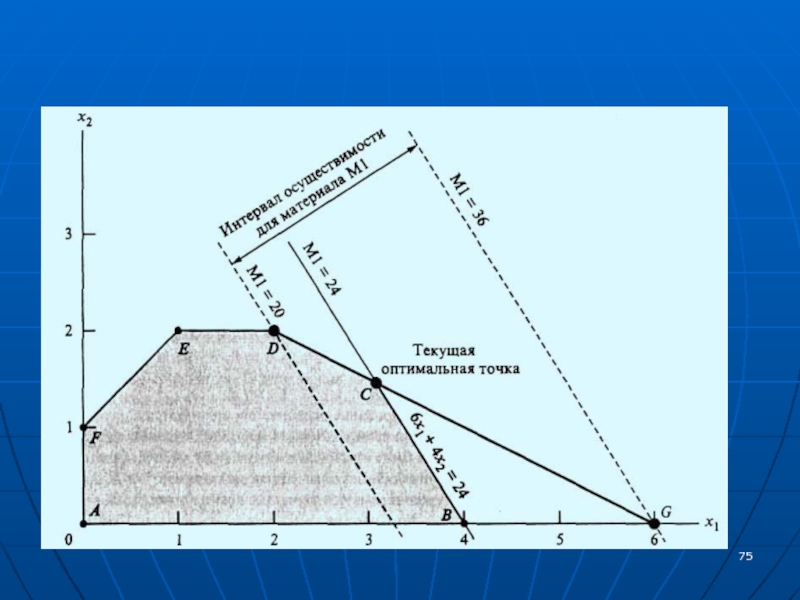
стоимость единиц этих ресурсов.Начнем с ограничения для сырья M1. Напомним, что в данной задаче оптимальное решение достигается в угловой точке С, являющейся точкой пересечения прямых, соответствующих ограничениям на сырье M1 и М2 (см. рис.)
Слайд 76При изменении уровня доступности материала M1 (увеличение или уменьшение текущего
уровня, равного 24 т) точка С оптимального решения "плывет" вдоль
отрезка DG. Любое изменение уровня доступности материала M1, приводящее к выходу точки пересечения С из этого отрезка, ведет к неосуществимости оптимального решения в точке С. Поэтому можно сказать, что концевые точки D = (2, 2) и G = (6, 0) отрезка DG определяют интервал осуществимости для ресурса M1. Количество сырья M1, соответствующего точке D = (2, 2), равно 6x1 + 4x2 = 6*2 + 4*2 = 20 т.Слайд 77Аналогично количество сырья, соответствующего точке G = (6, 0), равно
36 т.
Таким образом, интервал осуществимости для ресурса M1 составляет
20 ≤ M1 ≤ 36 (здесь через M1 обозначено количество материала M1). Если мы определим М1 как M1 = 24 + D1, где D1 — отклонение количества материала М1 от текущего уровня в 24 т, тогда последние неравенства можно переписать как 20 ≤ 24 + D1 ≤ 36 или -4 ≤ D1 ≤ 12. Слайд 78Это означает, что текущий уровень ресурса M1 может быть уменьшен
не более чем на 4 т и увеличен не более
чем на 12 т. В этом случае гарантируется, что оптимальное решение будет достигаться в точке С — точке пересечения прямых, соответствующих ограничениям на ресурсы M1 и М2.Теперь вычислим стоимость единицы материала M1. При изменении количества сырья M1 от 20 до 36 тонн, значения целевой функции z будут соответствовать положению точки С на отрезке DG. Обозначив через y1 стоимость единицы ресурса M1, получим следующую формулу:
Слайд 80Если точка С совпадает с точкой D = (2, 2),
то z = 5*2 + 4*2 = 18 (тысяч д.e.),
если же точка С совпадает с точкой G = (6, 0), тогда z = 5*6 + 4*0= 30 (тысяч д.e.). Отсюда следует, чтоСлайд 81Этот результат показывает, что изменение количества ресурса M1 на одну
тонну (если общее количество этого ресурса не меньше 20 и
не больше 36 тонн) приводит к изменению в оптимальном решении значения целевой функции на 750 д.е.Теперь рассмотрим ресурс М2.