Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Примеры спектров непериодических сигналов
Содержание
- 1. Примеры спектров непериодических сигналов
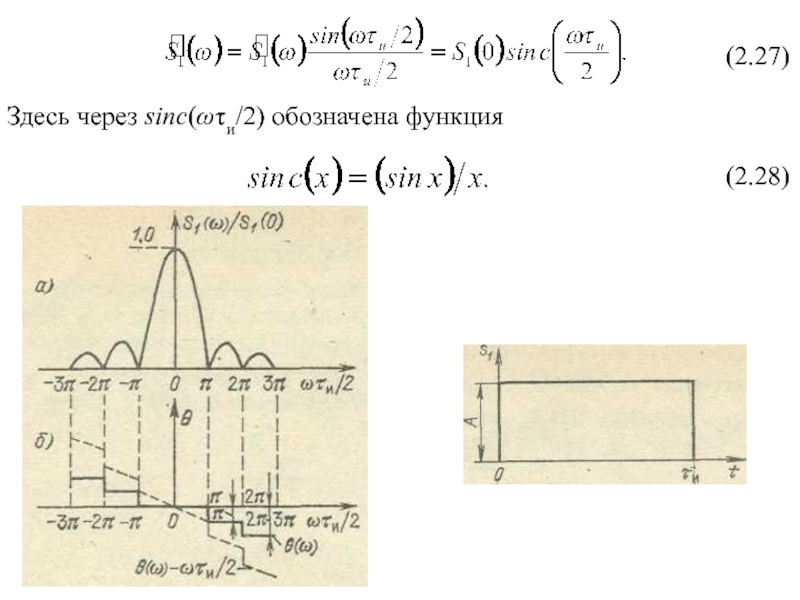
- 2. Здесь через sinc(ωτи/2) обозначена функция(2.27)(2.28)
- 3. Треугольный импульс(2.29)
- 4. Спектральная плотность положительного прямоугольного импульса длительностью по
- 5. Колоколообразный (гауссовский) импульс(2.32)(2.33)Дополним показатель степени до квадрата
- 6. Переходя к новой переменной , получаем Учитывая,
- 7. соответствует гауссовский импульсс длительностью и амплитудой Гауссовский
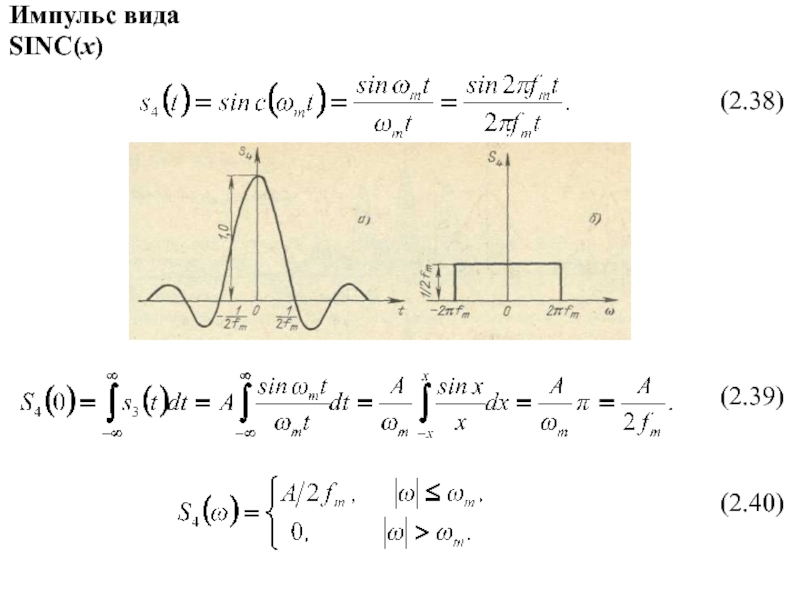
- 8. Импульс вида SINC(x)(2.38)(2.39)(2.40)
- 9. Бесконечно короткий импульс с единичной площадью(дельта-функция)Амплитуды импульсов
- 10. при одновременном условии(2.43)(2.44)Для импульса sin(2πfmx)/πx , площадь
- 11. Применительно к исходным функциям, дельта-функция должна быть
- 12. (2.49)В математике соотношение (2.49) называется фильтрующим(стробирующим) свойством
- 13. Спектральная плотность дельта-функции может быть получена и
- 14. (2.52)(2.53)Энергия единичного импульса бесконечно велика. При спектральномрассмотрении
- 15. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Примеры спектров непериодических сигналов
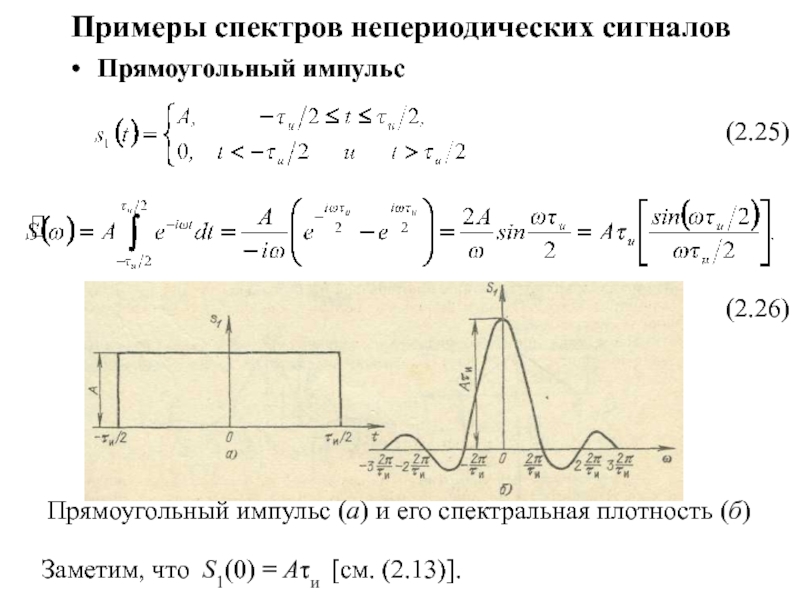
Прямоугольный импульс
(2.25)
(2.26)
Прямоугольный импульс (а) и его спектральная
плотность (б)
Слайд 4Спектральная плотность положительного прямоугольного импульса
длительностью по аналогии с формулой
(2.26) и с учетом сдвига
середины импульса на время τи/4 относительно
точки t=0Спектральная плотность отрицательного импульса
Суммарная спектральная плотность двух импульсов
(2.30)
Спектральная плотность треугольного импульса [интеграл от s'2(t)]
Множитель Aτи/2=S2(0) – площадь треугольного импульса.
(2.31)
Слайд 5Колоколообразный (гауссовский) импульс
(2.32)
(2.33)
Дополним показатель степени до квадрата суммы
где d определяется
из условия
, откуда
Таким образом, (2.33) можно привести к виду
(2.34)
Слайд 6Переходя к новой переменной
, получаем
Учитывая, что входящий в
это выражение интеграл равен ,
окончательно получаем
(2.35)
Колоколообразный (гауссовский)
импульс (а) и его спектральная плотность (б)Слайд 7соответствует гауссовский импульс
с длительностью
и амплитудой
Гауссовский импульс и его
спектр выражаются одинаковыми
функциями и обладают свойством симметрии: для получения
одной
из них по заданной другой достаточно заменить t на ω или наоборот.
Полоса, определяемая на уровне е−1/2 от максимального значения,
равна 2b=2/а=2∙2τи=4/τи, а коэффициент
.
(2.36)
(2.37)
Гауссовскому спектру
.
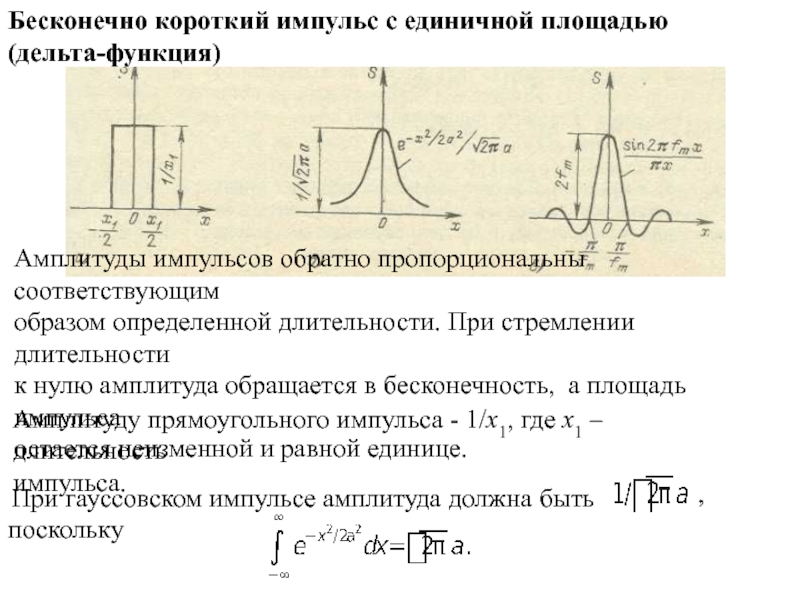
Слайд 9Бесконечно короткий импульс с единичной площадью
(дельта-функция)
Амплитуды импульсов обратно пропорциональны соответствующим
образом
определенной длительности. При стремлении длительности
к нулю амплитуда обращается в бесконечность,
а площадь импульсаостается неизменной и равной единице.
Амплитуду прямоугольного импульса - 1/x1, где x1 –длительность
импульса.
При гауссовском импульсе амплитуда должна быть
поскольку
,
Слайд 10
при одновременном условии
(2.43)
(2.44)
Для импульса sin(2πfmx)/πx , площадь которого равна единице,
амплитуда
равна 2fm (при х=0). Длительность импульса (главного лепестка) обратно пропорциональна
параметру fm.При устремлении параметров x1 и а к нулю, а fm к бесконечности
все три функции можно определить следующим образом:
Функция δ(х), обладающая указанными свойствами, называется
единичным импульсом, импульсной функцией или
дельта-функцией (а также функцией Дирака).
Слайд 11Применительно к исходным функциям, дельта-функция должна
быть определена выражениями
При сдвиге
импульса по оси х на величину х0
(2.45)
(2.46)
(2.51)
(2.47)
(2.48)
Слайд 12
(2.49)
В математике соотношение (2.49) называется фильтрующим
(стробирующим) свойством дельта-функции.
Спектральная плотность дельта-функции
вещественна и равна
единице для всех частот. Из этого также
вытекает, что ФЧХ спектрадельта-функции δ(х) равна нулю для всех частот. Это означает, что
все гармонические составляющие единичного импульса при нулевых
начальных фазах, суммируясь, образуют пик бесконечно большой
величины, в момент времени t=0.
Аналогично функция δ(t−t0) имеет спектральную плотность
Свойства функции δ(х)
Слайд 13
Спектральная плотность дельта-функции может быть получена и с помощью преобразования
Фурье:
Используя свойство (2.49), находим
:
Правая часть равенства S(ω)=1 является размерной
единицей:это площадь импульса, численно равная единице. Если под δ(t0)
подразумевается импульс напряжения, то размерность S(ω) есть
вольт∙секунда (В∙с).
(2.50)
δ(t−t0) представить в виде обратного преобразования Фурье
(2.51)
Слайд 14(2.52)
(2.53)
Энергия единичного импульса бесконечно велика. При спектральном
рассмотрении это вытекает из
равенства Парсеваля [см. (2.24)],
правая часть которого при S(ω)=1 обращается
в бесконечность.
Рассмотрим теперь свойства δ(ω).
Все, что ранее было сказано относительно δ(t), справедливо и для
δ(ω) при замене t на ω и ω на t. По аналогии с выражением (2.51)
можем написать









![Примеры спектров непериодических сигналов (2.52)(2.53)Энергия единичного импульса бесконечно велика. При спектральномрассмотрении это вытекает из равенства (2.52)(2.53)Энергия единичного импульса бесконечно велика. При спектральномрассмотрении это вытекает из равенства Парсеваля [см. (2.24)], правая часть которого](/img/thumbs/a104e6b7c0440bcfd911ce73162e2c70-800x.jpg)



















