Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Принятие решений в интеллектуальных системах
Содержание
- 1. Принятие решений в интеллектуальных системах
- 2. ИсточникиЛаричев О.И. Теория и методы принятия решений.
- 3. Модели ПРМодели которые строит экономист, отличается от
- 4. Задачи исследования операцийПод ИО понимают применение математических,
- 5. Задачи ИО обычно сводятся к задачам линейного программирования
- 6. Пример.Задача о пищевом рационеИмеется 4 вида продуктов
- 7. Столы и стульяЦех может производить столы и
- 8. Транспортные задачи (модели) Транспортные модели описывают перемещение
- 9. Ограничения1.Суммарное количество груза, направляемое из каждого пункта
- 10. Решение3. Суммарная стоимость всех перевозокЭто типичная задача линейного программирования
- 11. Виды моделейТМ могут быть закрытыми или открытыми
- 12. Методы решения:Метод северо-западного угла.Метод наименьшей стоимости.Метод штрафных функций.Метод циклических перестановок.Метод потенциалов.
- 13. ПримерС трех кирпичных заводов перевозятся кирпичи
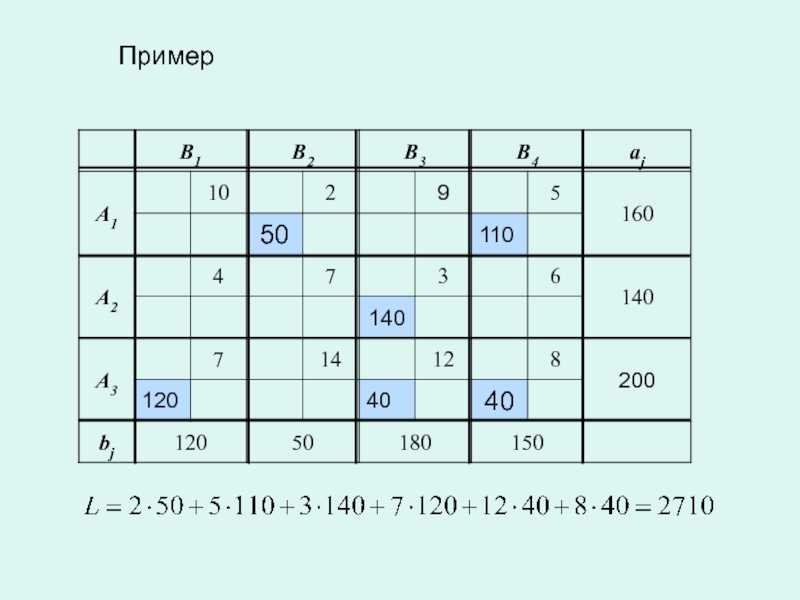
- 14. Пример
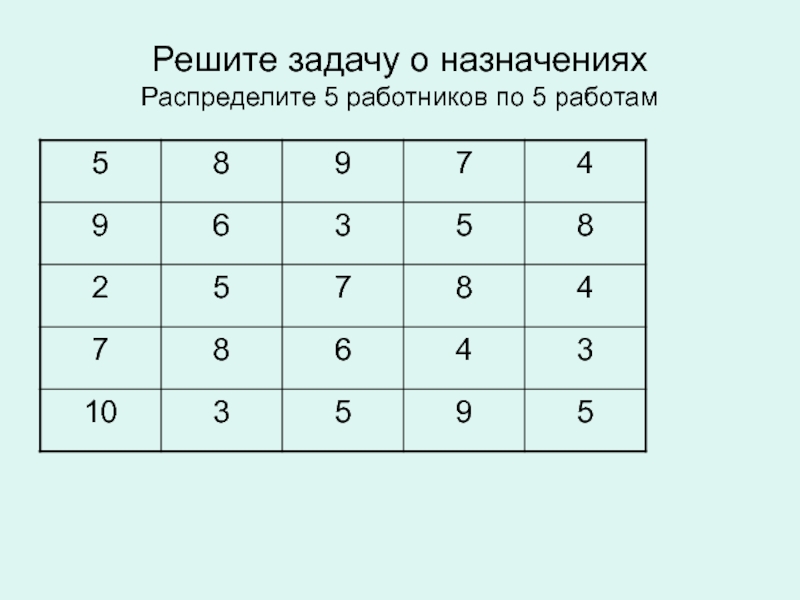
- 15. Решите задачу о назначениях Распределите 5 работников по 5 работам
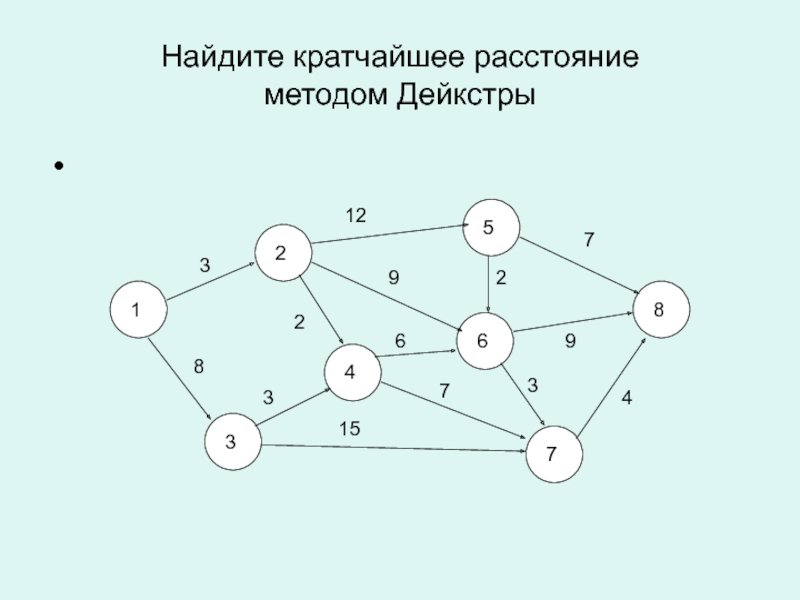
- 16. Найдите кратчайшее расстояние методом Дейкстры 125346873812297152967343
- 17. Даны 7 предметов с объемами:5, 10, 6,
- 18. Продажа сельхозпродуктовФермер вырастил урожай и ему надо
- 19. Далееg1x1+g2x2+…+gnxn=Σgixic1x1+c2x2+…+cnxn=Σcixi, Σgixi=0
- 20. Комбинаторные задачи К этой группе задач относятся:Задача
- 21. Задача коммивояжераИзвестна как задача о бродячем торговце.
- 22. Задача коммивояжера часто встречается на практике Определение
- 23. Математическая модель задачиИмеется N городов, которые должен
- 24. Далее 1, если коммивояжер следует из i в
- 25. Завдача может быть решена методом перебора, Количество вариантов будет составлять (n-1)! Так при n=4 (4-1)!=2*3=6
- 26. Методы решения1. Метод перебора.2. Жадный алгоритм.3. Метод ветвей и границ.4. Деревянный алгоритм.5. Генетический алгоритм.
- 27. Жадный алгоритм Заключается в нахождении наикратчайшего расстояния
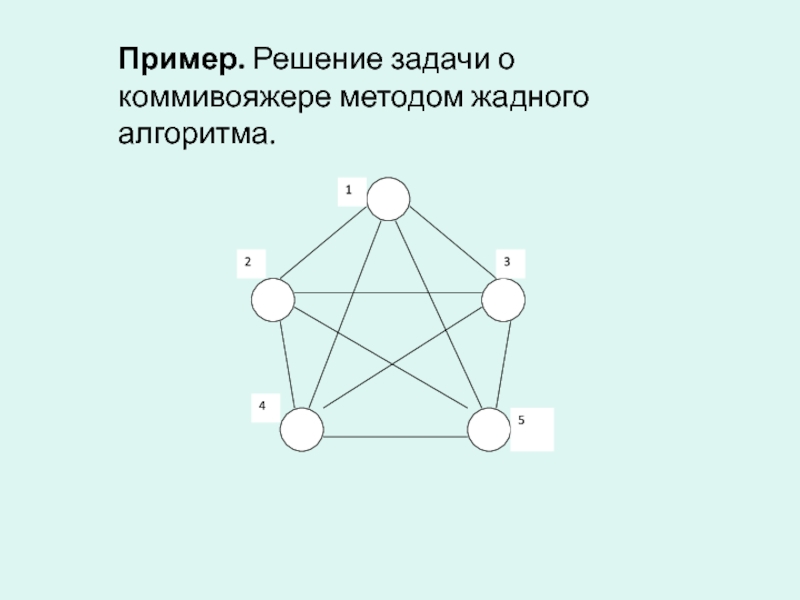
- 28. Пример. Решение задачи о коммивояжере методом жадного алгоритма.
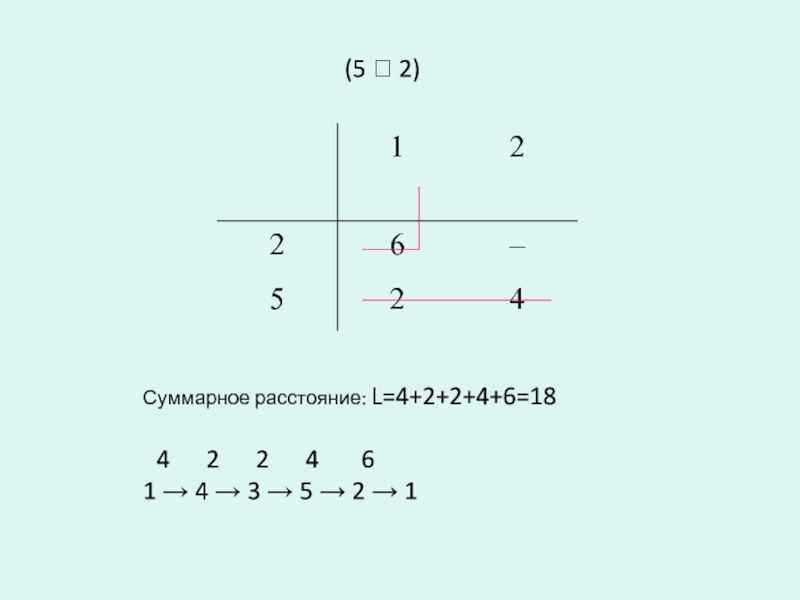
- 29. Матрица расстояний(1 4)
- 30. (4 3)(3 5)
- 31. Суммарное расстояние: L=4+2+2+4+6=18 4
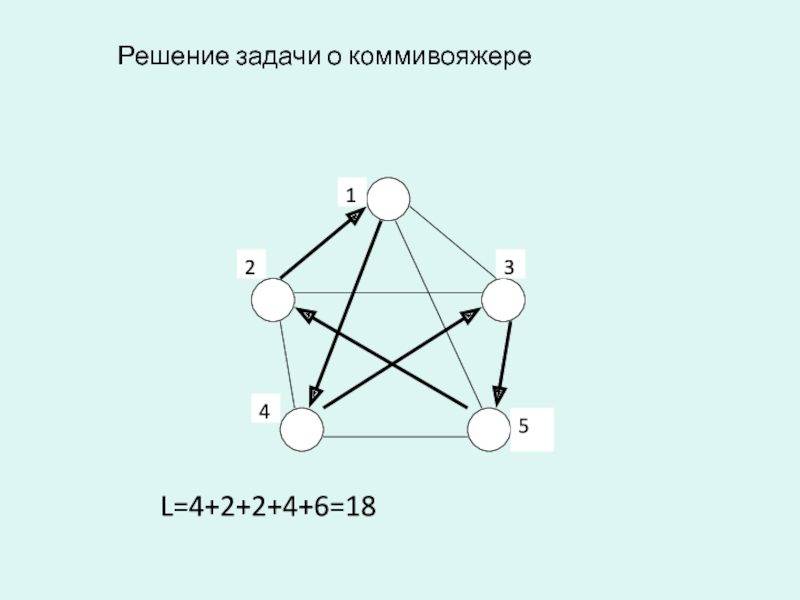
- 32. Решение задачи о коммивояжере L=4+2+2+4+6=18
- 33. Появление многокритериальностиПри широком применении
- 34. КлассификацияПодходы ИО и принятия решений (ПР) существенно
- 35. Два пространства пространство переменных (x1, x2) и
- 36. Критериис1с2С1 – уменьшение безработицы (%);С2 – увеличение ВНП (%).110.50.5С1=0.1*Х1 + 0.9*Х2С2=0.5*Х1 + 0.5*Х2S
- 37. Методы решения многокритер. задач ПРСведения к однокр-ой задачиОптимизация по ПаретоСвертка критериевМетод контр.пок.Выдел.осн.критер
- 38. ПримерПредположим, что приоритет первого критерия – 60%, второго – 40%.
- 39. Множество ПаретоЧто касается точек дуги АВ, то
- 40. Методы решения:Метод уступок.Метод идеальной точки.Метод ограничений.Метод анализа иерархий.
- 41. Пример. Строительство нового аэропорта около города М.
- 42. Оценка многокритериальных альтернатив. Подход аналитической иерархииПостановка задачи:Дано:
- 43. СтруктуризацияЦельКритерииПлощадкиСтроительство аэропортаСтоимость
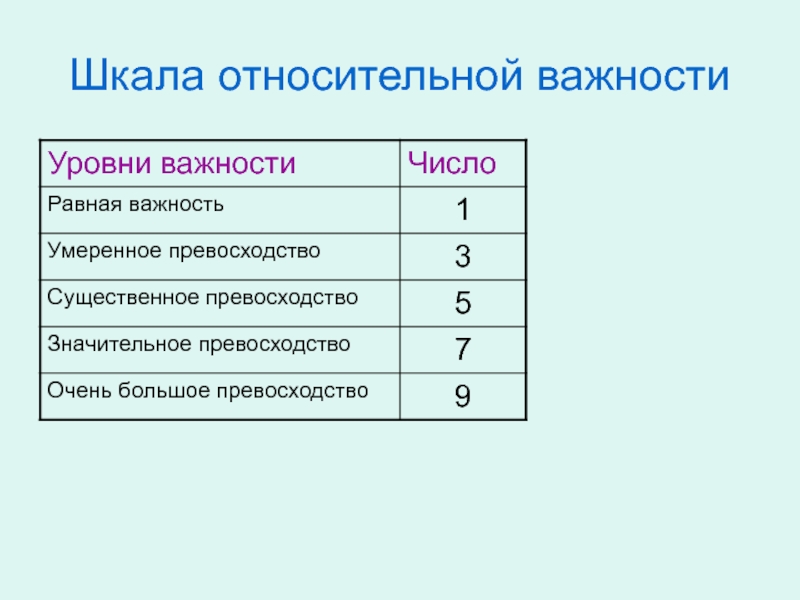
- 44. Шкала относительной важности
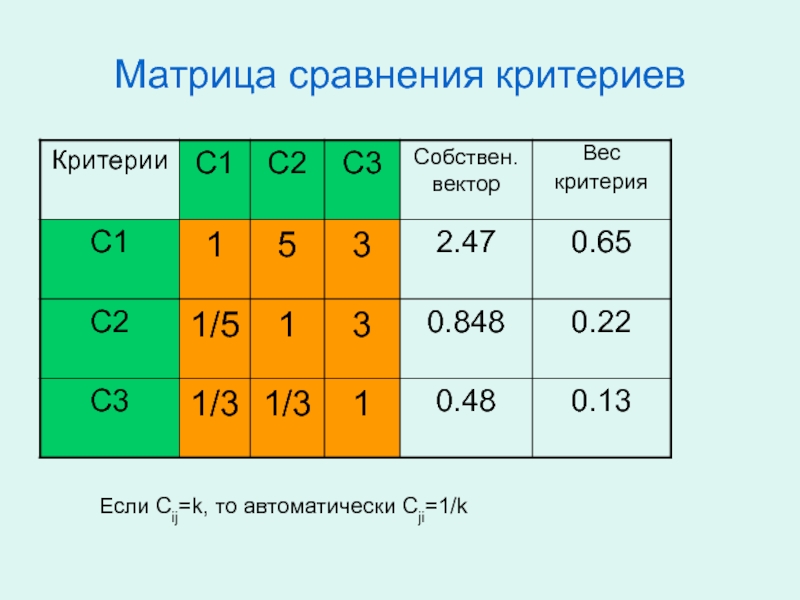
- 45. Матрица сравнения критериевЕсли Сij=k, то автоматически Сji=1/k
- 46. Расчет собственного вектора
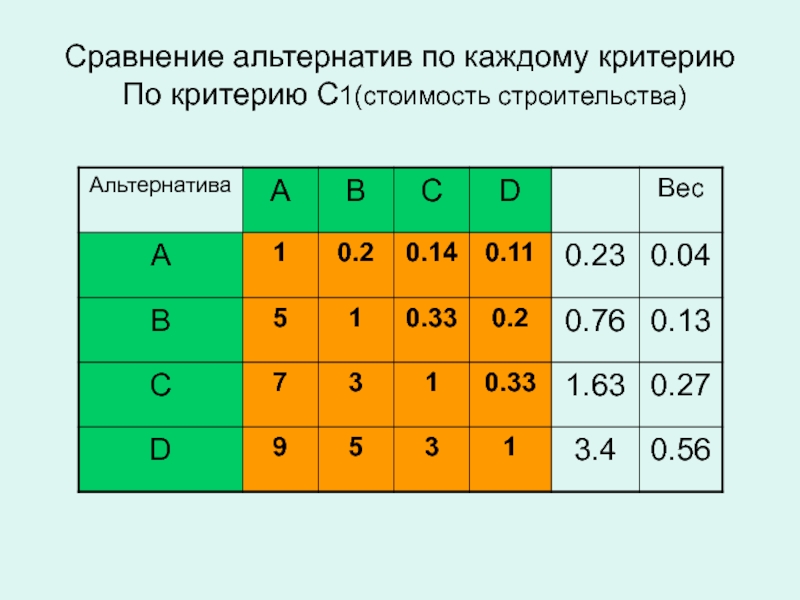
- 47. Сравнение альтернатив по каждому критерию По критерию C1(стоимость строительства)
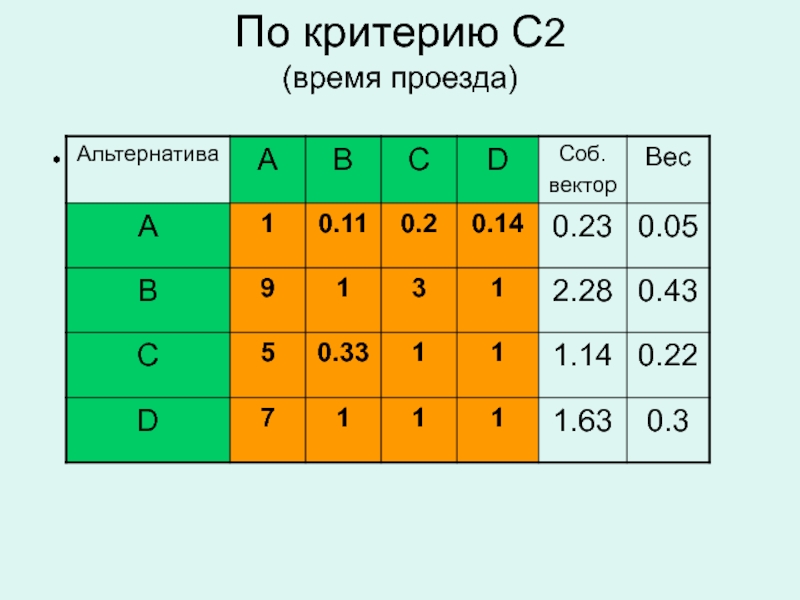
- 48. По критерию С2 (время проезда)
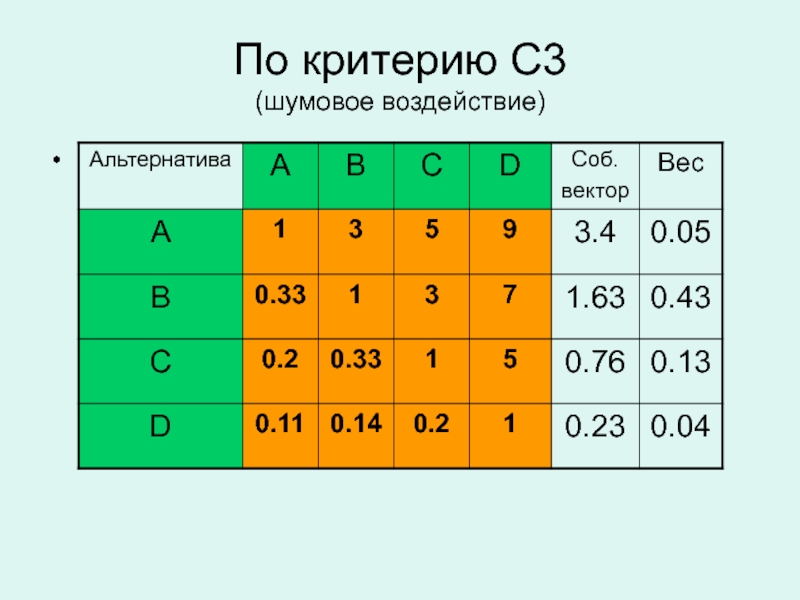
- 49. По критерию С3 (шумовое воздействие)
- 50. Синтез коэффициентов важностиОсуществляется по формуле:
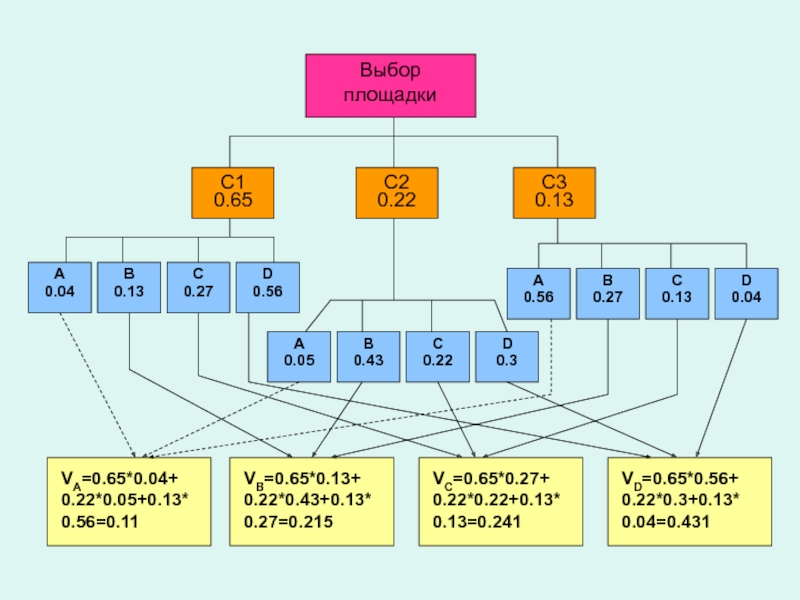
- 51. Выбор площадкиС10.65С20.22С30.13А0.04В0.13С0.27D0.56A0.05B0.43C0.22D0.3A0.56B0.27C0.13D0.04VA=0.65*0.04+ 0.22*0.05+0.13*0.56=0.11VB=0.65*0.13+ 0.22*0.43+0.13*0.27=0.215VC=0.65*0.27+ 0.22*0.22+0.13*0.13=0.241VD=0.65*0.56+ 0.22*0.3+0.13* 0.04=0.431
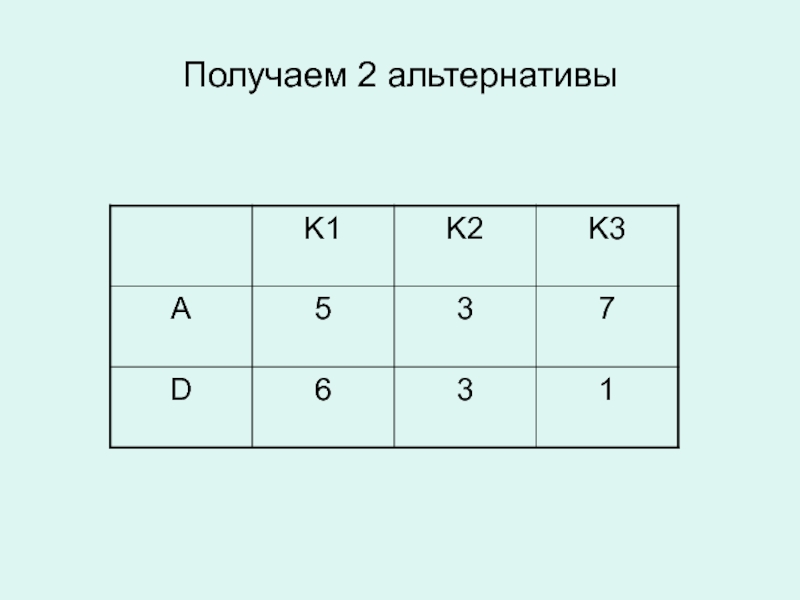
- 52. Получаем 2 альтернативы
- 53. Проверим остаточные знанияКлассификация методов принятия решений.Могут ли
- 54. ПродолжениеВ чем отличие метода наименьшей стоимости от
- 55. Слайд 55
- 56. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Принятие решений в интеллектуальных системах
Принятие решений это особый процесс человеческой
деятельности, направленный на выбор наилучшего варианта действий
Слайд 2Источники
Ларичев О.И. Теория и методы принятия решений. – М.:Логос, 2002
Моисеев
В.С. и др. Теория принятия решений: Учебное пособие, 2006
Орлов А.И.
Теория принятия решений. 2005Черноруцкий И.Г. Методы принятия решений, 2005
Таха, Хэмди А. Введение в исследование операций. 2001
Матвеев М.Г. И др. Модели и методы искусственного интеллекта. Применение в экономике. 2008
Слайд 3Модели ПР
Модели которые строит экономист, отличается от модели физика, математика,
инженера.
Физик, описывающий уравнениями состояние газа в закрытой камере, создает математическую
модель процесса.Модель экономиста описывает процессы, в которых важную роль играют люди: рабочие, продавцы, водители и т.д.
В жизни человеческое поведение в значительной степени непредсказуемо и сложно для моделирования
Модели, описывающие поведение людей, активно используются в исследовании операций (ИО), но в этом случае, люди не имеют свободы поведения.
Слайд 4Задачи исследования операций
Под ИО понимают применение математических, количественных методов для
обоснования решений во всех областях целенаправленной человеческой деятельности (Е.С.Вентцель)
Основными этапами
решения любой задачи в ИО являются: 1)построение модели;
2)выбор критерия оптимальности;
3)нахождение оптимального решения.
Классические задачи ИО: транспортная задача, задача о назначениях, сетевые модели, комбинаторные задачи и т.д.
Словесному описанию этих задач соответствует четкое математическое описание, представляющее собой математическую модель
Слайд 6Пример.Задача о пищевом рационе
Имеется 4 вида продуктов питания:
P1, P2,
P3, P4
Известна стоимость продуктов питания:
c1, c2, c3, c4 соответственно . Из этих продуктов необходимо составить пищевой рацион, который должен содержать:
- белков не менее b1 углеводов не менее b2 жиров не менее b3
Слайд 7Столы и стулья
Цех может производить столы и стулья.
На производство стула
идет 5 ед.материала, на производство стола – 20 ед.Стул требует 10 человеко-часов, стол – 15. Имеется 400 единиц материала (красного дерева) и 450 человеко-часов.
Прибыль при производстве стула – 45 у.е., стола – 80 у.е.
Сколько надо сделать стульев (x1) и столов (x2), чтобы получить максимальную прибыль?
Слайд 8Транспортные задачи (модели)
Транспортные модели описывают перемещение (перевозку) какого-либо товара
из пункта отправления (ПО) в пункт назначения (ПН).
В качестве
ПН могут быть магазины, рынки, склады и т.д. Назначение транспортной задачи – определение объемов перевозок из ПО в ПН с минимальной суммарной стоимостью перевозок.
Слайд 9Ограничения
1.Суммарное количество груза, направляемое из каждого пункта отправления во все
пункты назначения, должно быть равно запасу груза в данном пункте.
Это дает m условий равенств.2. Суммарное количество груза, доставляемое в каждый пункт назначения из всех пунктов отправления, должно быть равно заявке. Это дает n условий равенств
Слайд 11Виды моделей
ТМ могут быть закрытыми или открытыми
Закрытая модель –
это модель, в которой суммарная мощность поставщиков равна суммарному спросу
потребителей.В противном случае модель наз. открытой
Слайд 12Методы решения:
Метод северо-западного угла.
Метод наименьшей стоимости.
Метод штрафных функций.
Метод циклических перестановок.
Метод
потенциалов.
Слайд 13Пример
С трех кирпичных заводов перевозятся кирпичи на
4 строительные площадки.
Заданы: ежедневный объем выпуска (тыс.шт.)
Ежедневная потребность (тыс.шт.)
Надо
обеспечить минимальную стоимость перевозокСлайд 17Даны 7 предметов с объемами:
5, 10, 6, 8, 4, 12,
9 единиц (кг)
И ценностями:
2, 6, 4, 3, 5, 8, 7
единицОбъем рюкзака не должен превышать 40 кг
Загрузите рюкзак наилучшим образом.
Слайд 18Продажа сельхозпродуктов
Фермер вырастил урожай и ему надо вывезти его на
ярмарку. Продукты: картофель, капуста, морковь, свекла, огурцы, помидоры, яблоки.
Всего
7 видов с объемами:0.5, 1.0, 0.6, 0.8, 0.4, 1.2, 0.9
И ценностями:
2, 6, 4, 3, 5, 8, 7 тыс.руб.
Объем автофургона не должен превышать 4.0 т
Надо загрузить автофургон наилучшим образом.
Слайд 20Комбинаторные задачи
К этой группе задач относятся:
Задача теории расписаний.
Задача о коммивояжере
(задача о бродячем торговце).
Например, составление расписания по оптимальной обработке деталей.
Пусть имеется n – деталей и два станка токарный и фрезерный. Каждая деталь должна быть последовательно обработана на каждом из этих станков.
Как загрузить эти детали, чтобы время было минимальным? От выбора порядка обработки деталей зависят простои оборудования.
Слайд 21Задача коммивояжера
Известна как задача о бродячем торговце. Район, который должен
посетить бродячий торговец, содержит некоторое количество городов, расстояние между которыми
являются известными. Требуется найти маршрут, проходящий через все пункты по одному разу и возвращающийся в исходный. Если таких маршрутов много, требуется найти кратчайший из них.Слайд 22Задача коммивояжера часто встречается на практике
Определение маршрута развозки продуктов по
торговым точкам города так, чтобы суммарная длина пробега машины была
бы минимальной.Выбор минимальной по протяженности автобусной линии в городе, на ряде улиц которого возможно лишь одностороннее движение и фиксировано местоположение остановок автобусов.
Расстановка указателей в музее , когда известно местоположение каждого экспоната и расстояние между ними и требуется установить такой порядок осмотра, при котором затрачивается минимум времени на переходы между экспонатами.
Задача определения оптимального порядка обработки деталей.
Развозка почты.
Задача соединения отдельных пунктов линиями электропередач, водопровода и т.д.
Слайд 23Математическая модель задачи
Имеется N городов, которые должен обойти коммивояжер с
минимальными затратами. При этом на его маршрут накладываются два ограничения:
-
маршрут должен быть замкнутым, т.е. коммивояжер должен вернуться в тот город откуда начал движение;- в каждом из городов коммивояжер должен побывать точно один раз, т.е. надо обязательно обойти все города, при этом не побывав ни в одном городе дважды.
N – число городов,
dij – расстояние между i и j,
xij – матрица переходов,
Слайд 24Далее
1, если коммивояжер следует из i в j
хij=
0, иначе
Σxij=1 – выезжает
из каждого города 1 раз i
Σxij=1 – въезжает в каждый город 1 раз
j
xij>=0 xij={0,1} i,j=1,N
Слайд 25Завдача может быть решена методом перебора, Количество вариантов будет составлять
(n-1)!
Так при n=4 (4-1)!=2*3=6
Слайд 26Методы решения
1. Метод перебора.
2. Жадный алгоритм.
3. Метод ветвей и границ.
4.
Деревянный алгоритм.
5. Генетический алгоритм.
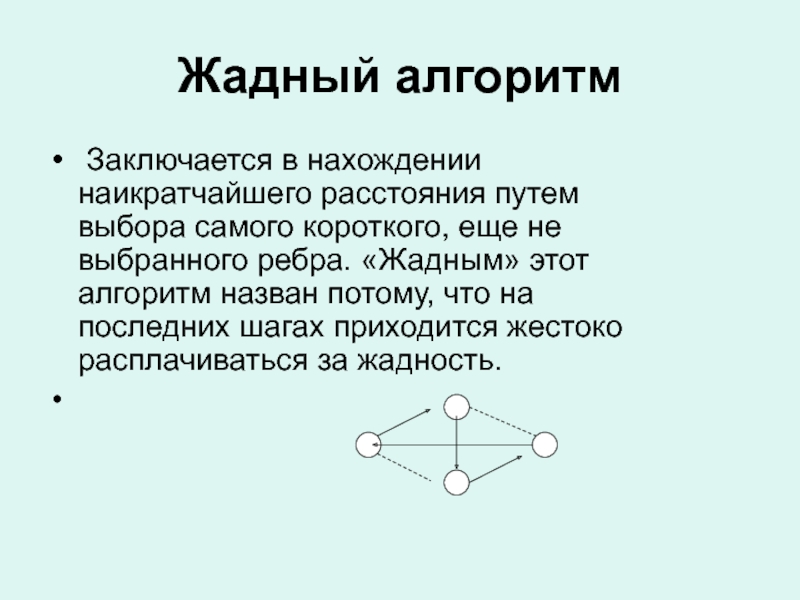
Слайд 27Жадный алгоритм
Заключается в нахождении наикратчайшего расстояния путем выбора самого
короткого, еще не выбранного ребра. «Жадным» этот алгоритм назван потому,
что на последних шагах приходится жестоко расплачиваться за жадность.Слайд 33
Появление многокритериальности
При широком применении методов исследования операций (ИО) аналитики
стали сталкиваться с задачами, где имеется не один, а несколько
критериев оценки качества решения.Слайд 34Классификация
Подходы ИО и принятия решений (ПР) существенно различаются, так как
они направлены на принципиально разные проблемы ПР.
Выделяют следующие проблемы:
Хорошо
структуризованные, или количественно сформулированные проблемы, - те, в которых существенные зависимости выявлены настолько хорошо, что могут быть выражены в числах или символах, получающих в конце концов численные оценки.Слабоструктуризованные, или смешанные проблемы, - те, которые содержат как качественные, так и количественные элементы, причем качественные, малоизвестные и неопределенные стороны проблем имеют тенденцию доминировать.
Слабоструктуризованные и неструктуризованные проблемы исследуются в рамках научного направления, называемого принятием решений при многих критериях.
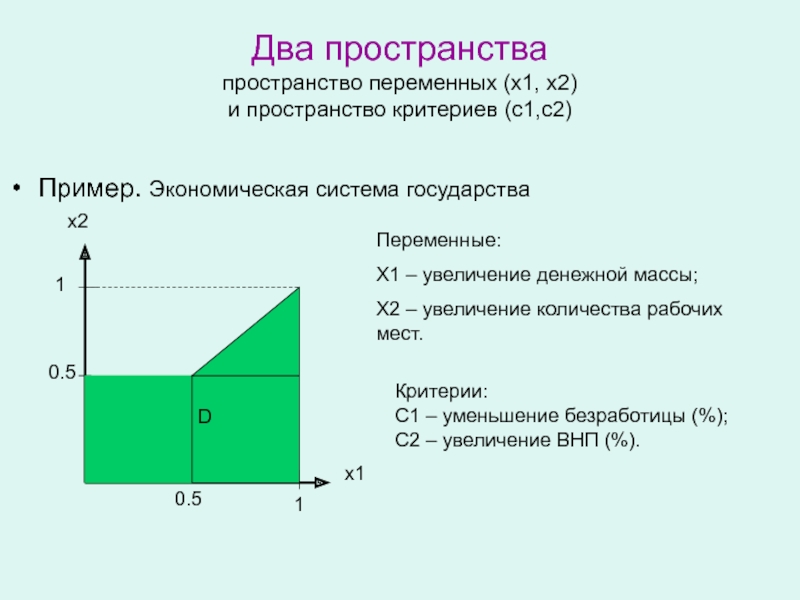
Слайд 35Два пространства
пространство переменных (x1, x2)
и пространство критериев (c1,c2)
Пример. Экономическая система
государства
х2
х1
1
1
0.5
0.5
Переменные:
Х1 – увеличение денежной массы;
Х2 – увеличение количества рабочих
мест. D
Критерии:
С1 – уменьшение безработицы (%);
С2 – увеличение ВНП (%).
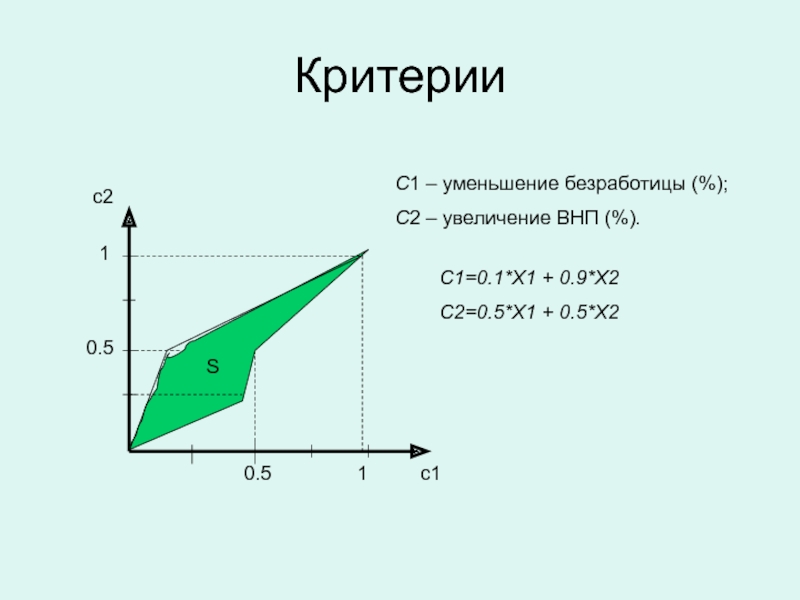
Слайд 36Критерии
с1
с2
С1 – уменьшение безработицы (%);
С2 – увеличение ВНП (%).
1
1
0.5
0.5
С1=0.1*Х1 +
0.9*Х2
С2=0.5*Х1 + 0.5*Х2
S
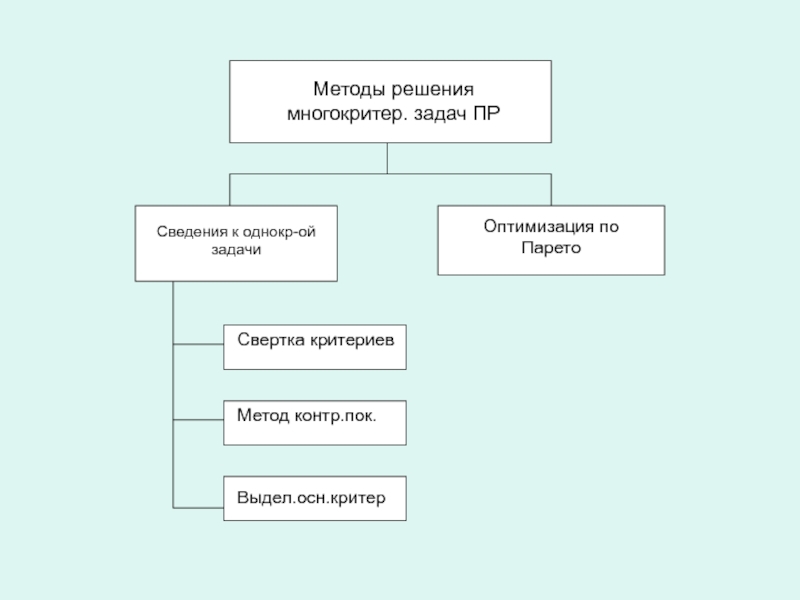
Слайд 37Методы решения многокритер. задач ПР
Сведения к однокр-ой задачи
Оптимизация по Парето
Свертка
критериев
Метод контр.пок.
Выдел.осн.критер
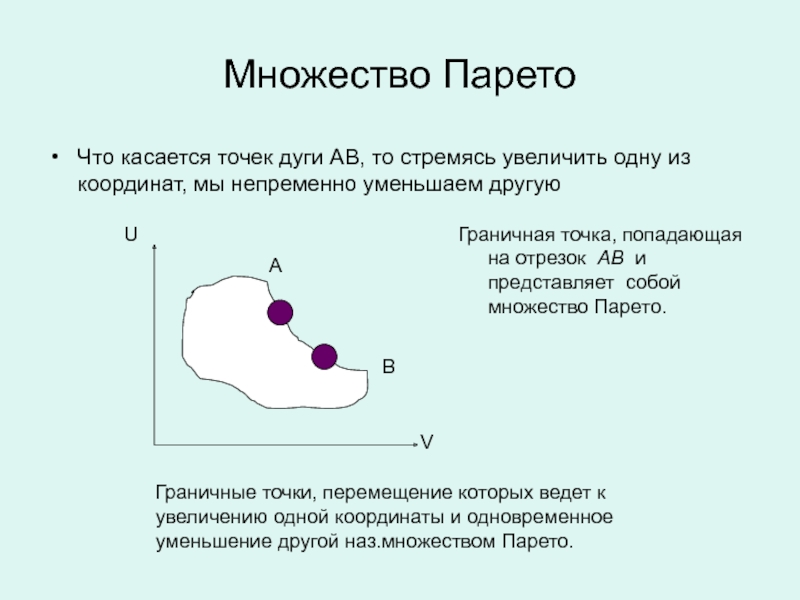
Слайд 39Множество Парето
Что касается точек дуги АВ, то стремясь увеличить одну
из координат, мы непременно уменьшаем другую
U
V
A
B
Граничная точка, попадающая на отрезок
АB и представляет собой множество Парето.Граничные точки, перемещение которых ведет к увеличению одной координаты и одновременное уменьшение другой наз.множеством Парето.
Слайд 40Методы решения:
Метод уступок.
Метод идеальной точки.
Метод ограничений.
Метод анализа иерархий.
Слайд 41Пример. Строительство нового аэропорта около города М.
Необходимо выбрать площадку.
Критерии:
Стоимость
постройки
Расстояние от города
Минимальное шумовое воздействие
Видно, что все эти критерии противоречивы.
Предположим,
что комиссия отобрала для строительства аэропорта 4 варианта. Площадки A, B, C, D.Для оценки альтернатив используется метод аналитической иерархии.
Слайд 42Оценка многокритериальных альтернатив. Подход аналитической иерархии
Постановка задачи:
Дано: общая цель (или)
цели решения задачи;
Критериев – N, альтернатив – n
Требуется: выбрать наилучшую
альтернативуЭтапы:
Структуризация задачи в виде иерархической структуры с несколькими уровнями: цели – критерии – альтернативы
Далее ЛПР выполняет по парные сравнения элементов каждого уровня. Результаты сравнений переводятся в числа (таблица).
Вычисляются коэф. важности для элементов каждого уровня.
Определяется наилучшая альтернатива.
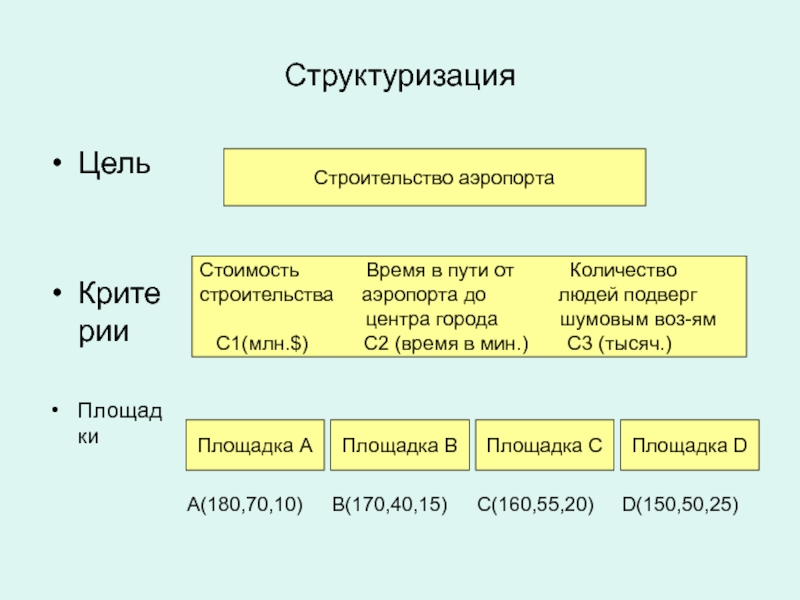
Слайд 43Структуризация
Цель
Критерии
Площадки
Строительство аэропорта
Стоимость Время в пути
от Количество
строительства аэропорта до
людей подвергцентра города шумовым воз-ям
С1(млн.$) C2 (время в мин.) С3 (тысяч.)
Площадка А
Площадка B
Площадка C
Площадка D
A(180,70,10)
B(170,40,15)
C(160,55,20)
D(150,50,25)
Слайд 51Выбор площадки
С1
0.65
С2
0.22
С3
0.13
А
0.04
В
0.13
С
0.27
D
0.56
A
0.05
B
0.43
C
0.22
D
0.3
A
0.56
B
0.27
C
0.13
D
0.04
VA=0.65*0.04+ 0.22*0.05+0.13*0.56=0.11
VB=0.65*0.13+ 0.22*0.43+0.13*0.27=0.215
VC=0.65*0.27+ 0.22*0.22+0.13*0.13=0.241
VD=0.65*0.56+ 0.22*0.3+0.13* 0.04=0.431
Слайд 53Проверим остаточные знания
Классификация методов принятия решений.
Могут ли решения быть допустимыми?
Укажите
математические методы ПР.
Какой класс математических моделей ПР является наиболее распространенным?
Сформулируйте
общую постановка задачи линейного программирования.Какова цель решения транспортных задач (ТЗ).
Сформулируйте общую постановку ТЗ.
Укажите методы решения ТЗ
Какой метод ТЗ является опорным.
Приведите способ решения ТЗ методом наименьшей стоимости, штрафных функций.
Слайд 54Продолжение
В чем отличие метода наименьшей стоимости от метода С-З угла.
Какой
план является оптимальным
Сформулируйте идею построения потенциального плана
Что такое потенциальный план.
В
чем отличие ТЗ с неправильным балансом от задачи с правильным балансом.Каков алгоритм решения ТЗ с неправильным балансом?
Когда требуется решение ТЗ по критерию времени?
Дайте алгоритм решения ТЗ по критерию времени.
Сформулируйте задачу о назначениях. Метод решения.
Методы поиска кратчайших расстояний
Сформулируйте задачу о рюкзаке. Методы решения.