Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Проецирование окружности
Содержание
- 1. Проецирование окружности
- 2. АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ОКРУЖНОСТЕЙ Если плоскость окружности
- 3. ПРОЕЦИРОВАНИЕРис.1. Проецирование окружности
- 4. Для любой прямоугольной аксонометрической проекции большая ось
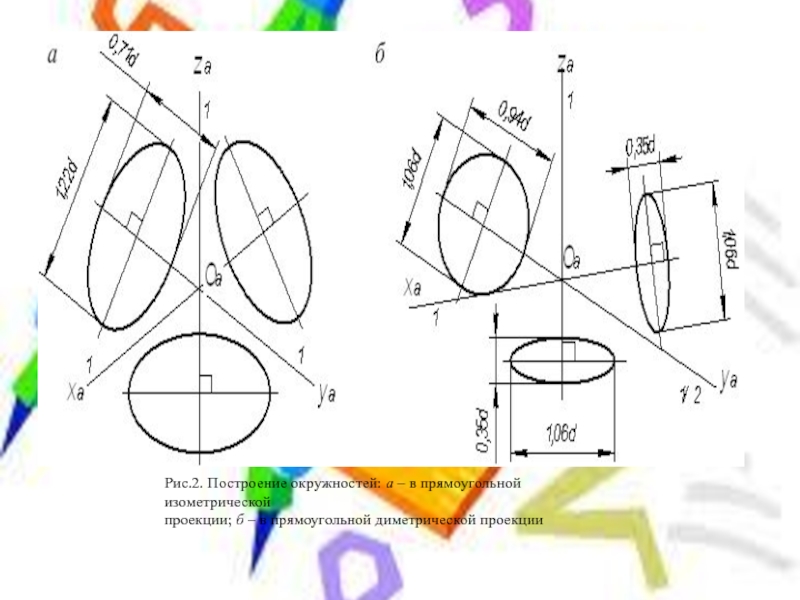
- 5. Рис.2. Построение окружностей: а – в прямоугольной изометрической проекции; б – в прямоугольной диметрической проекции
- 6. ЭЛЛИПСЭллипс представляет собой множество точек плоскости, сумма расстояний
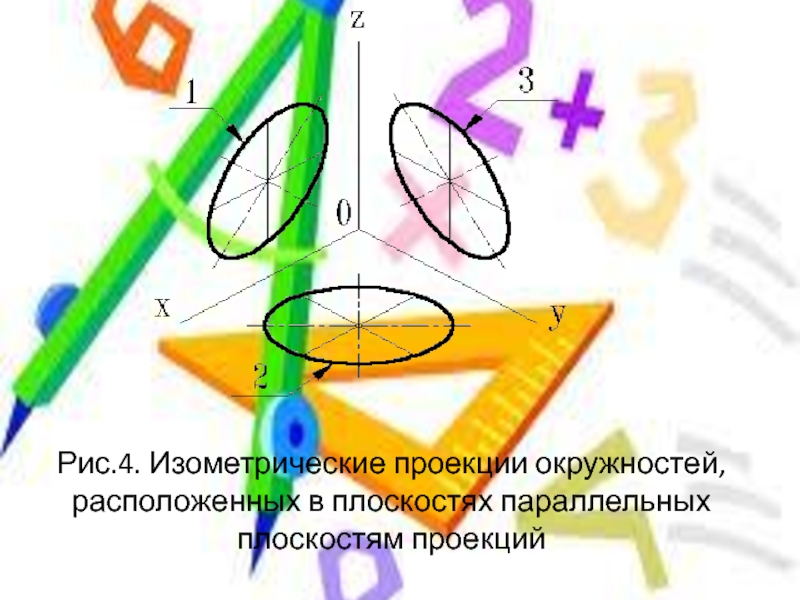
- 7. Рис.4. Изометрические проекции окружностей, расположенных в плоскостях параллельных плоскостям проекций
- 8. Рис.5. Диметрические проекции окружностей, расположенных в плоскостях параллельных плоскостям проекций
- 9. РАССМОТРИМ ПОШАГОВО ПРОЕЦИРОВАНИЕ ОКРУЖНОСТИ
- 10. ШАГ 1
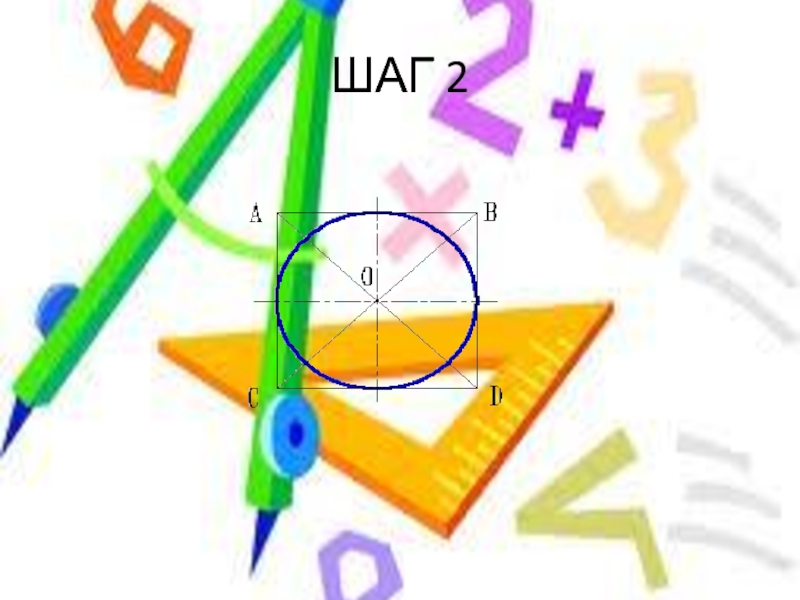
- 11. ШАГ 2
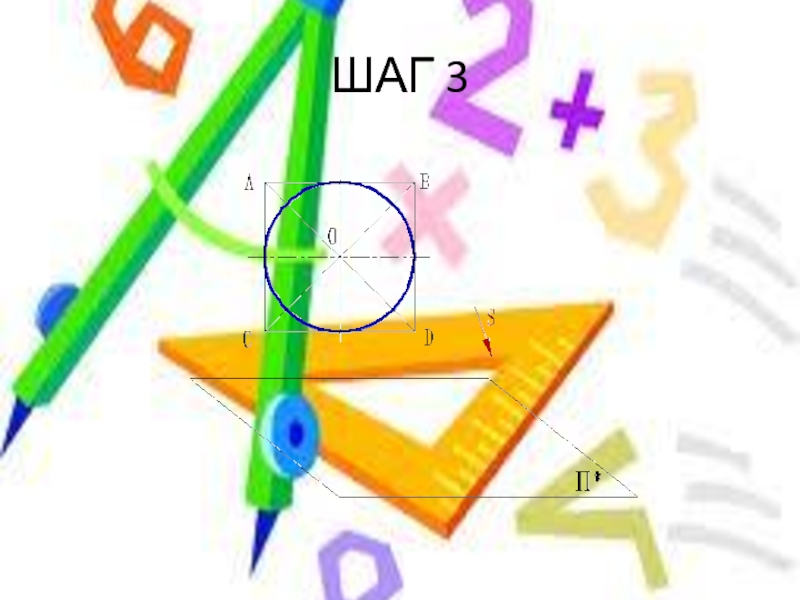
- 12. ШАГ 3
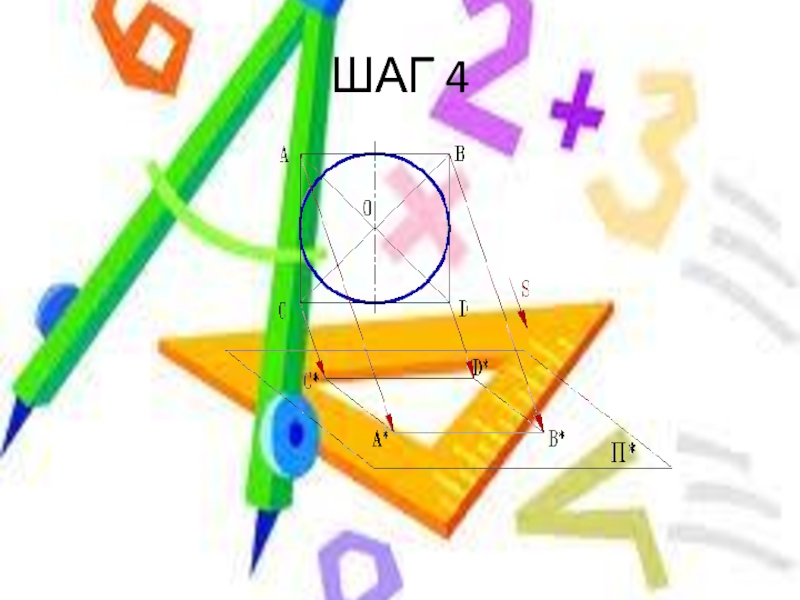
- 13. ШАГ 4
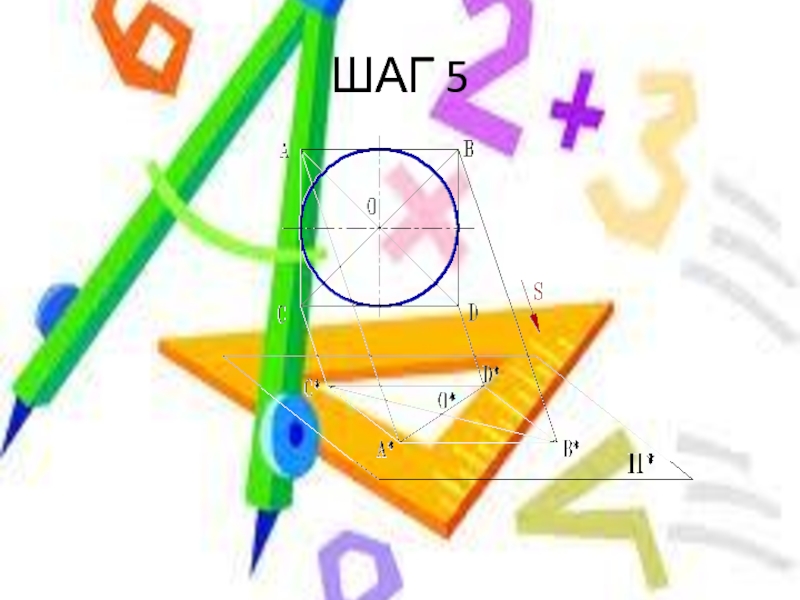
- 14. ШАГ 5
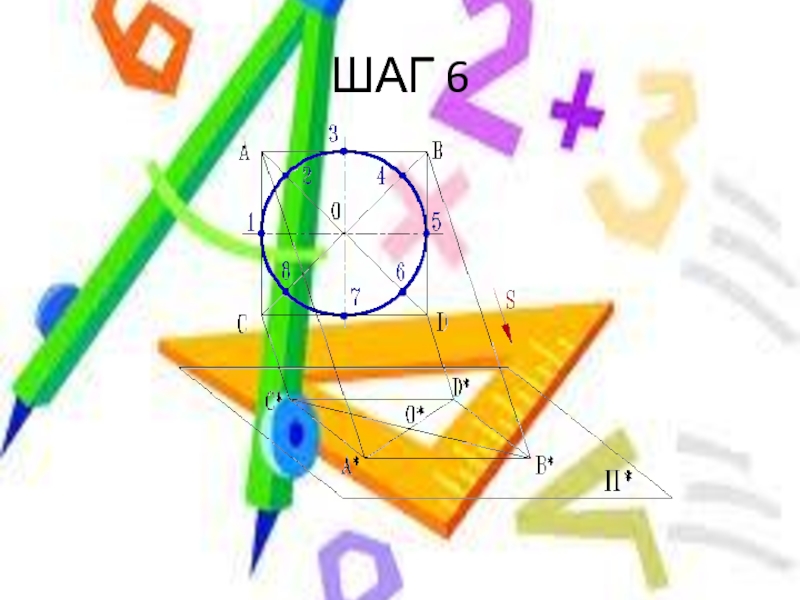
- 15. ШАГ 6
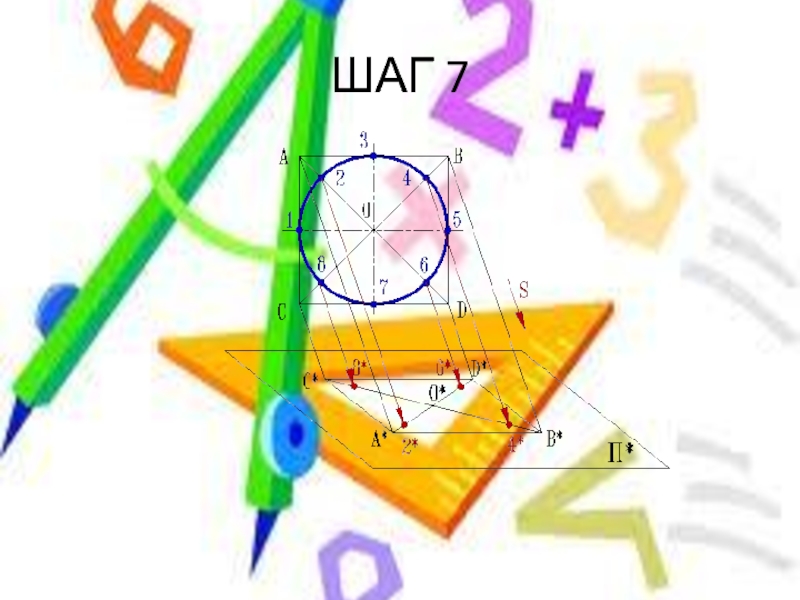
- 16. ШАГ 7
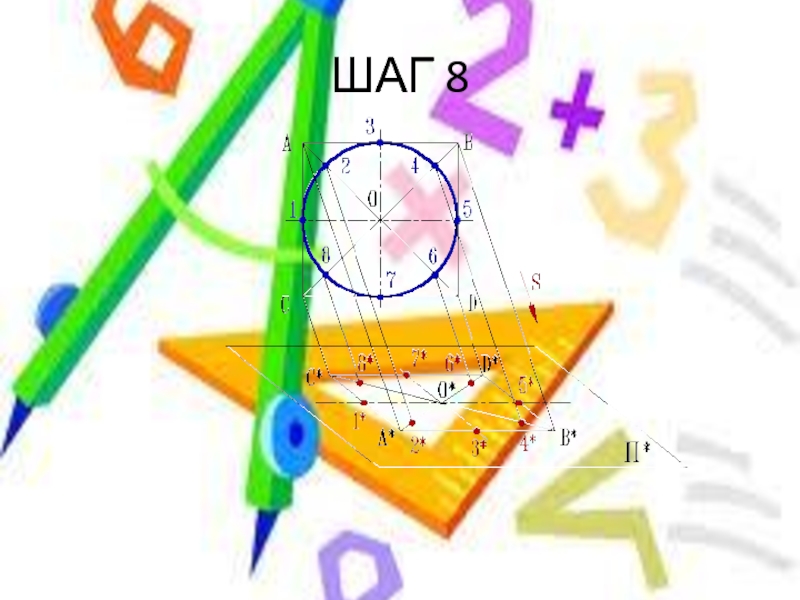
- 17. ШАГ 8
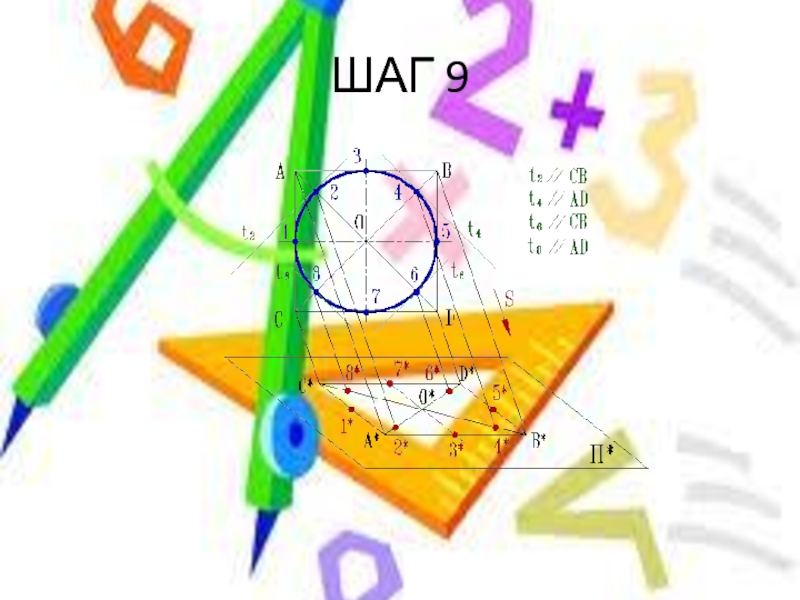
- 18. ШАГ 9
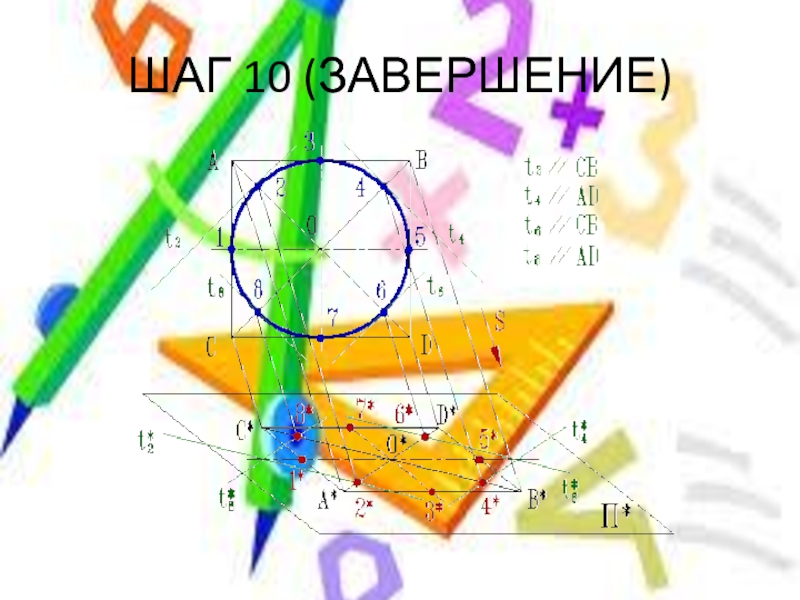
- 19. ШАГ 10 (ЗАВЕРШЕНИЕ)
- 20. СПАСИБО ЗА ВНИМАНИЕ!
- 21. Скачать презентанцию
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ОКРУЖНОСТЕЙ Если плоскость окружности не параллельна и не перпендикулярна плоскости аксонометрических проекций, то окружность проецируется на нее в виде эллипса. Очевидно, что большой осью эллипса будет являться проекция
Слайды и текст этой презентации
Слайд 2
АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ОКРУЖНОСТЕЙ
Если плоскость окружности не параллельна и не перпендикулярна
плоскости аксонометрических проекций, то окружность проецируется на нее в виде
эллипса. Очевидно, что большой осью эллипса будет являться проекция того диаметра окружности, который параллелен плоскости аксонометрических проекций, а малой осью – проекция диаметра, перпендикулярного к первому и наклоненного к картинной плоскости под наибольшим углом. Определим направления и размеры больших и малых осей эллипсов для окружностей, расположенных в плоскостях, параллельных плоскостям проекций.Слайд 4
Для любой прямоугольной аксонометрической проекции большая ось эллипса перпендикулярна к
одной из проекций координатных осей, а малая – совпадает с
направлением этой оси .Для запоминания этого положения можно воспользоваться следующим утверждением: большая ось эллипса перпендикулярна к отсутствующей оси, где термин «отсутствующая» означает «отсутствующая в названии». Например, горизонтальную плоскость проекций можно назвать плоскостью хОу, т. е. в названии отсутствует ось Oz, а значит, большая ось эллипса, в который проецируется горизонтальная окружность, должна быть перпендикулярна к аксонометрической проекции Oaza оси Oz. Большая ось эллипса, в который проецируется окружность, параллельна фронтальной плоскости проекций (плоскости xOz), будет перпендикулярна к оси Оу, а большая ось эллипса, в который проецируется окружность, параллельная плоскости yOz, – перпендикулярна к оси Ох.Слайд 5Рис.2. Построение окружностей: а – в прямоугольной изометрической
проекции; б – в прямоугольной диметрической проекции
Слайд 6ЭЛЛИПС
Эллипс представляет собой множество точек плоскости, сумма расстояний от каждой из
которых до двух данных точек (фокусов) этой плоскости постоянна и
превышает расстояние между фокусами. В качестве исходных данных для построения конкретного эллипса обычно служат направления и размеры большой АВ и малой CD осейРис.3. Построение эллипса
по двум диаметрам