Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сила упругости 1
Содержание
- 1. Сила упругости 1
- 2. FупрmgСила упругости – сила, возникающая при деформации
- 3. Условия возникновения силы упругости -
- 4. С целью упрощения расчетов используются следующие допущения
- 5. Причины деформацииПри изменении расстояния между атомами изменяются
- 6. Виды деформаций
- 7. Основные типы упругой деформации
- 8. Основные типы упругой деформации
- 9. Основные типы упругой деформации
- 10. Основные типы упругой деформации
- 11. Перемещения – переход точек тела в новое
- 12. Кроме линейных деформаций, связанных с изменением размеров
- 13. От чего зависит сила упругости при растяжении?Сила упругости зависит от растяжения пружины
- 14. От чего зависит сила упругости?абсолютное растяжение или
- 15. Сила упругости прямо пропорциональна абсолютному удлинению (растяжению) тела
- 16. Формула закона Гука ( в проекции
- 17. Что называется жесткостью тела? Коэффициент жесткости
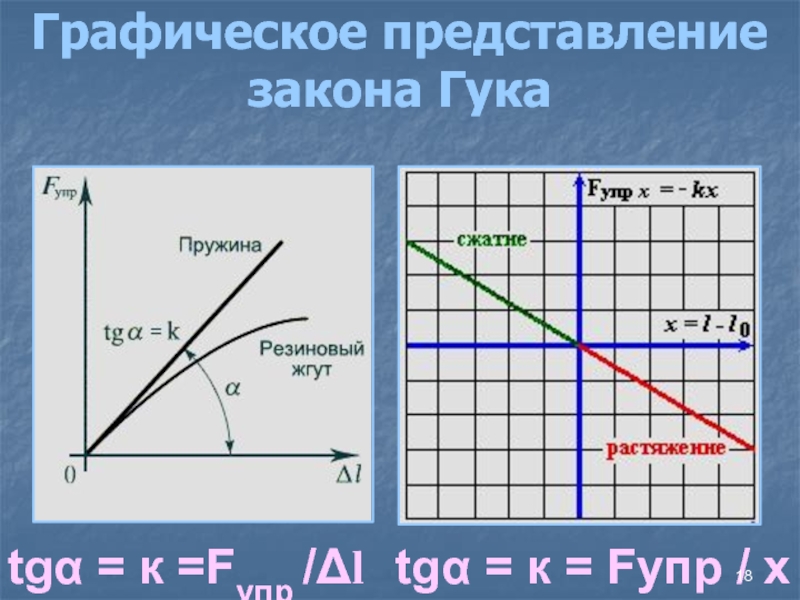
- 18. Графическое представление закона Гукаtgα = к =Fупр /Δltgα = к = Fупр / х
- 19. Определите жесткость пружиныНа графике отменим точку и
- 20. Закон Гука для малых упругих деформаций
- 21. Закон Гука при изгибе Закон Гука
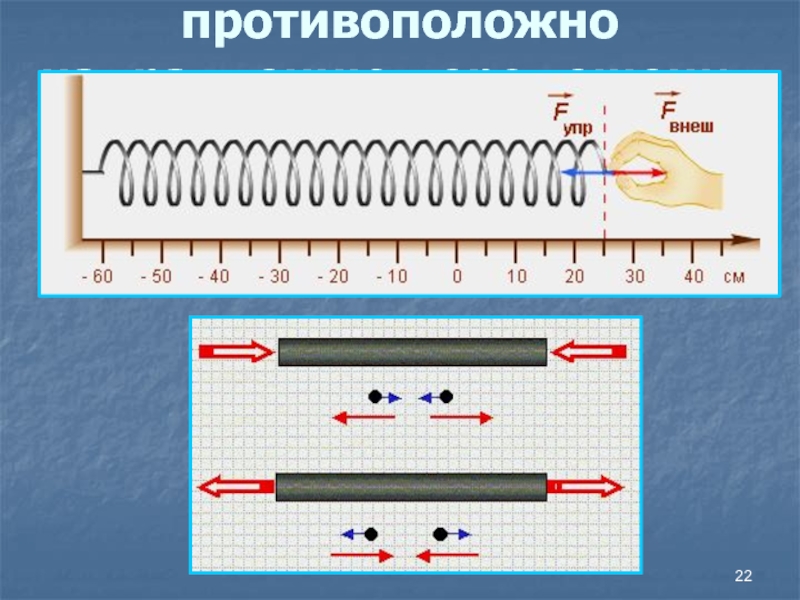
- 22. Направление силы упругости: противоположно направлению перемещения частиц при деформации
- 23. В физике закон Гука принято записывать в
- 24. Механическое напряжение Механическое напряжение – это
- 25. При упругой малой деформации механическое напряжение прямо
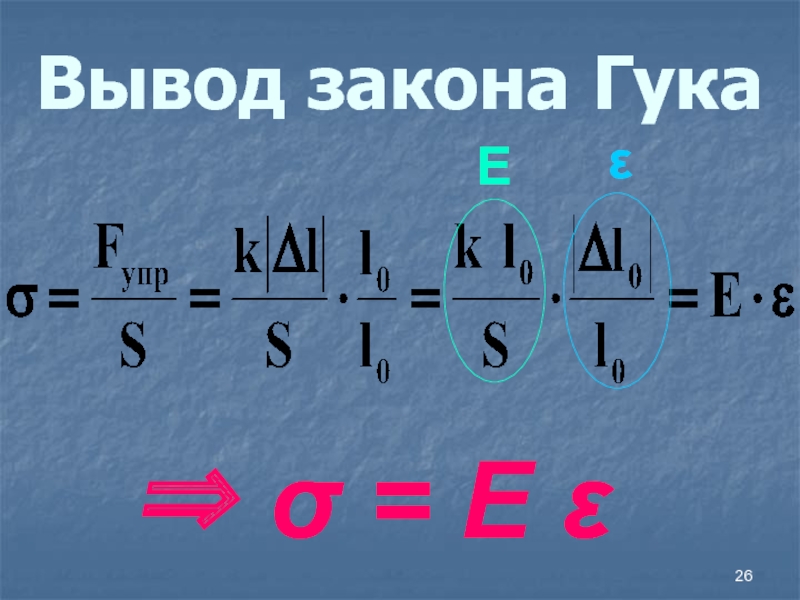
- 26. Вывод закона ГукаЕε
- 27. Модуль упругости - Е Модуль Юнга
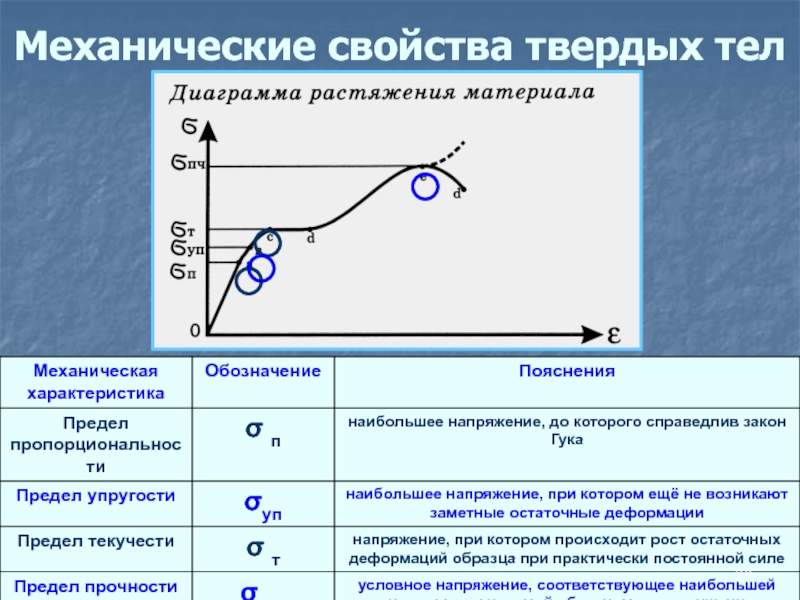
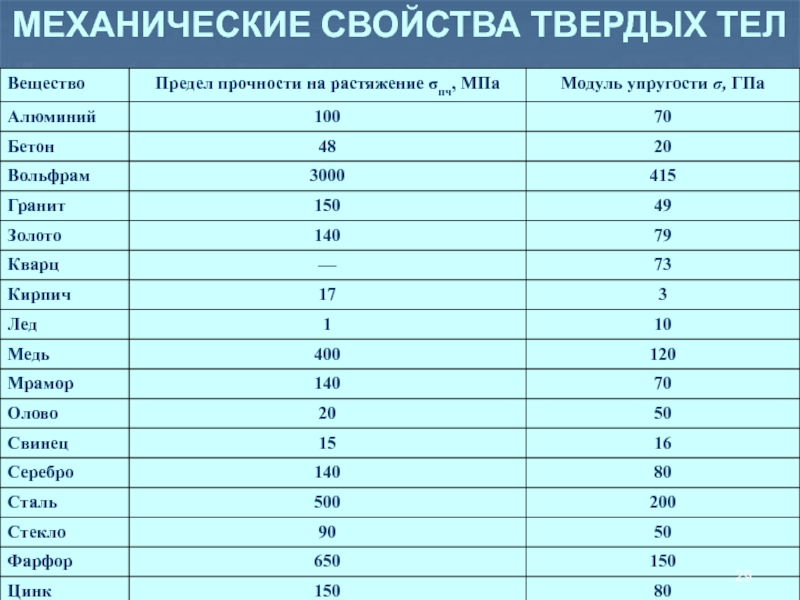
- 28. Механические свойства твердых тел
- 29. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ
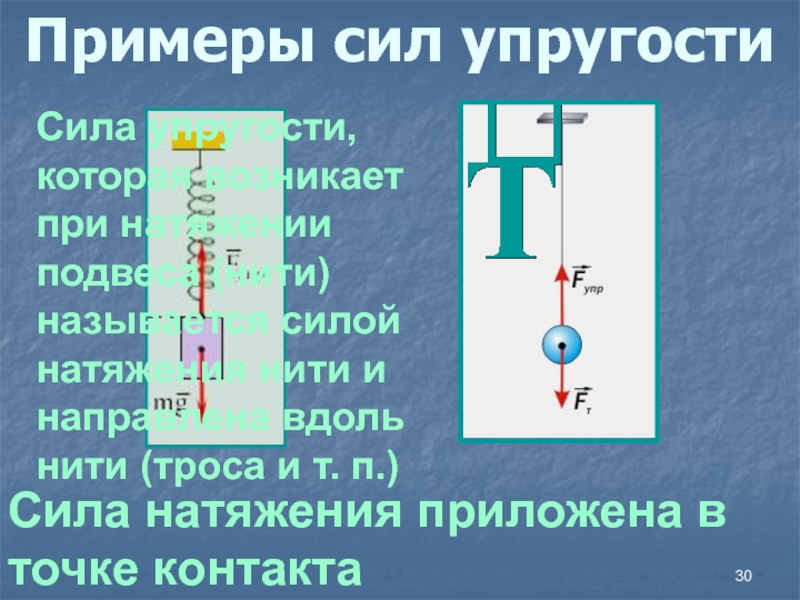
- 30. Примеры сил упругостиСила натяжения приложена в точке
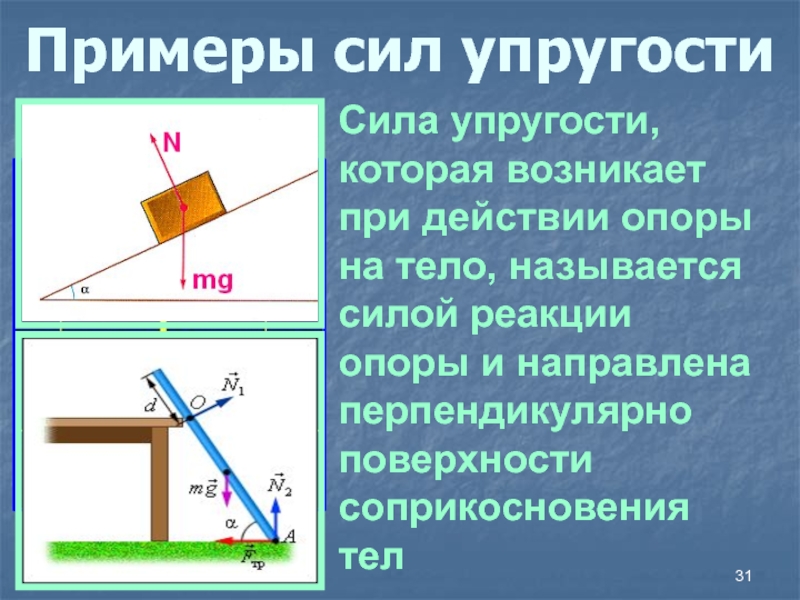
- 31. Примеры сил упругостиСила упругости, которая возникает при
- 32. Динамометр В пределах применимости закона Гука
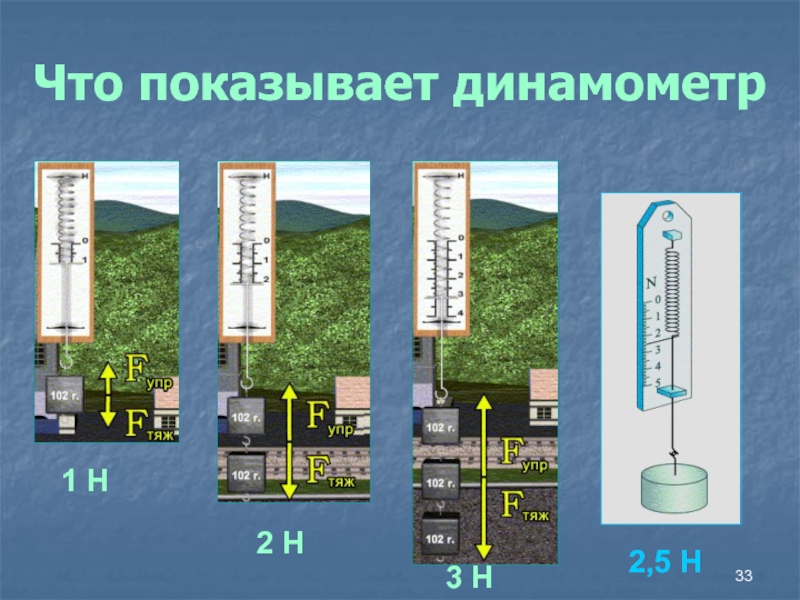
- 33. Что показывает динамометр1 Н2 Н3 Н2,5 Н
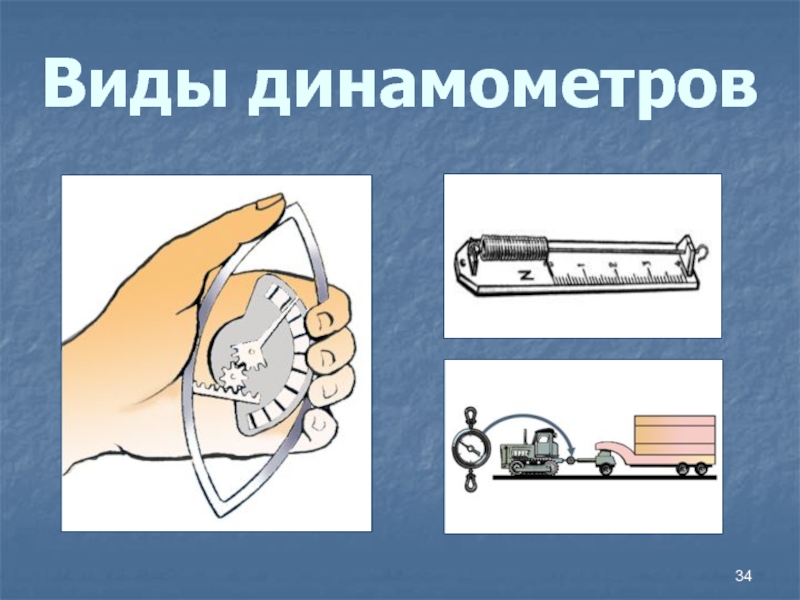
- 34. Виды динамометров
- 35. Итоги лекции
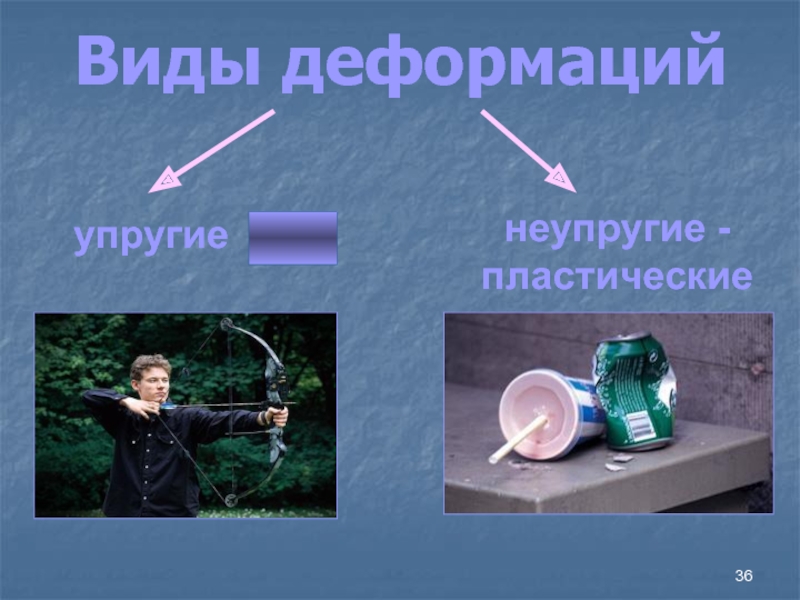
- 36. Виды деформацийупругиенеупругие - пластические
- 37. Когда справедлив закон Гука?
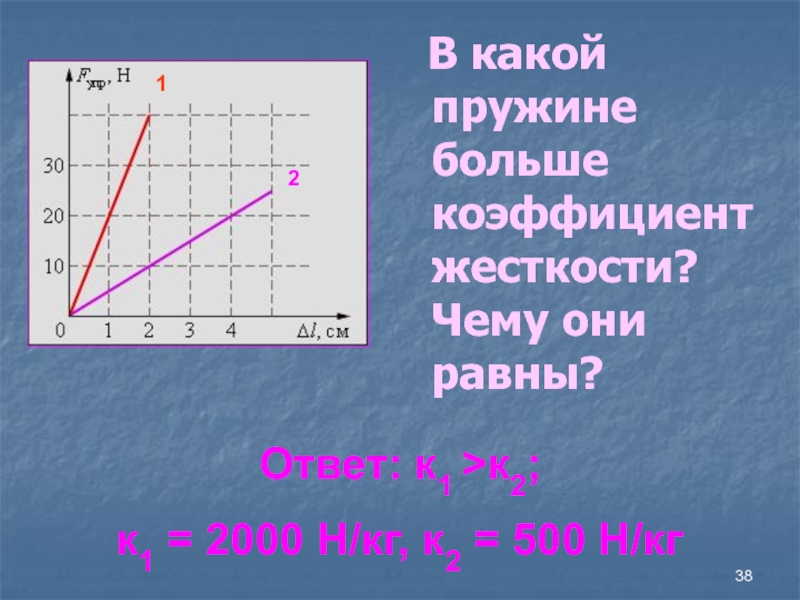
- 38. В какой пружине больше коэффициент жесткости?
- 39. Решите задачуОтвет: жесткость пружины равна 9,8 Н/м
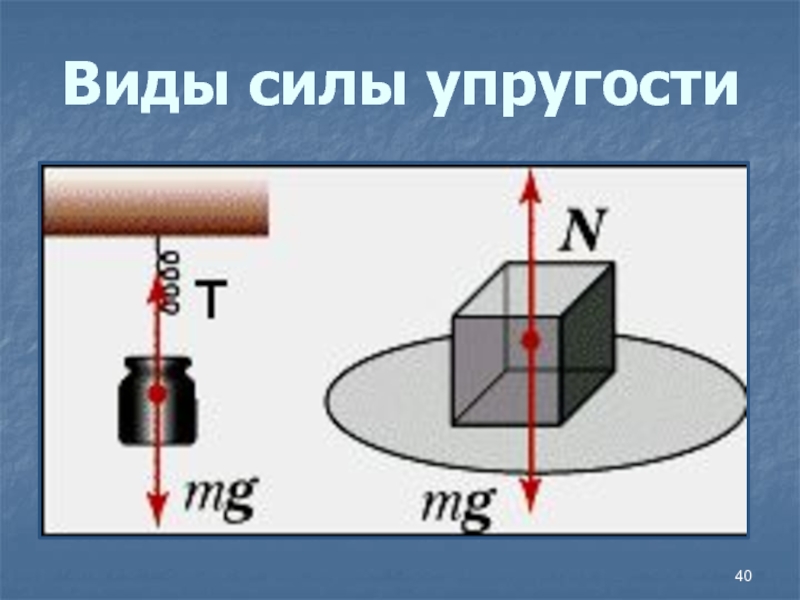
- 40. Виды силы упругости
- 41. Какие деформации изображены?
- 42. Деформации в жизни
- 43. Деформации в жизни
- 44. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Fупр
mg
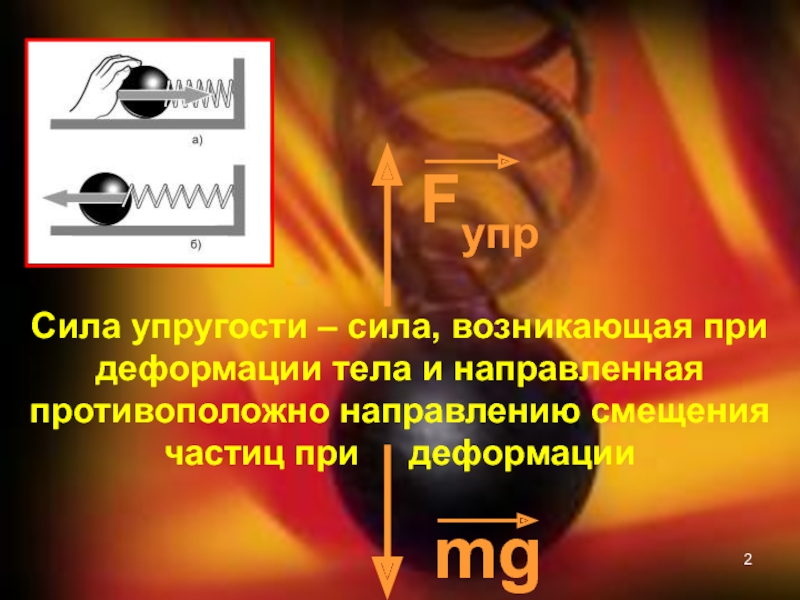
Сила упругости – сила, возникающая при деформации тела и направленная
противоположно направлению смещения частиц при деформации
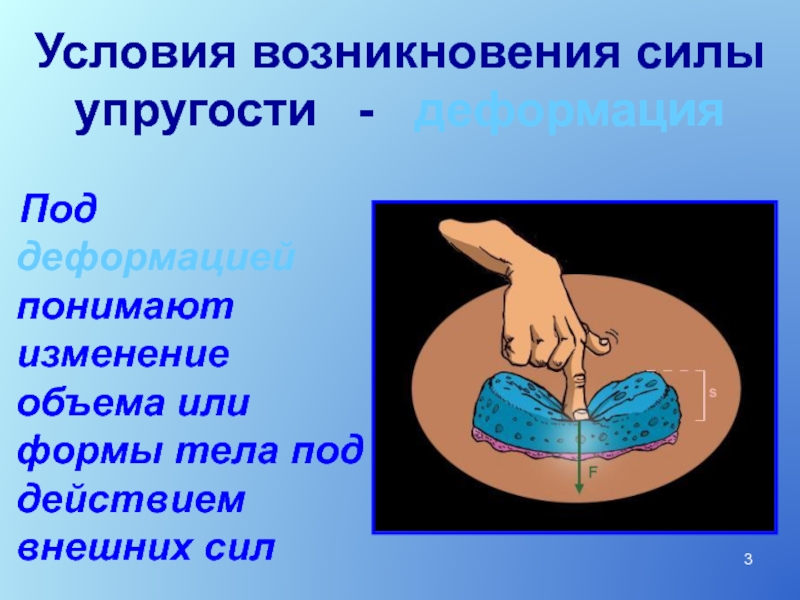
Слайд 3Условия возникновения силы упругости - деформация
Под
деформацией понимают изменение объема или формы тела под действием внешних
силСлайд 4С целью упрощения расчетов используются следующие допущения о свойствах материала. 1.
Материал считается однородным, если его свойства во всех точках одинаковы. 2.
Материал считается изотропным, если его свойства во всех направлениях одинаковы. 3. Материал обладает свойством идеальной упругости, вследствие которой деформируемое тело полностью восстанавливает свою форму и размеры после снятия нагрузки независимо от величин нагрузок и температуры тела. 4. Материал обладает свойством сплошности, то есть способностью сплошь (без пустот) заполнять пространство, ограниченное поверхностью тела. Вследствие этого материал считается непрерывным, что позволяет использовать для определения напряжений и деформаций математический аппарат дифференциального и интегрального исчисления .Слайд 5Причины деформации
При изменении расстояния между атомами изменяются силы взаимодействия между
ними, которые стремятся вернуть тело в исходное состояния. Поэтому силы
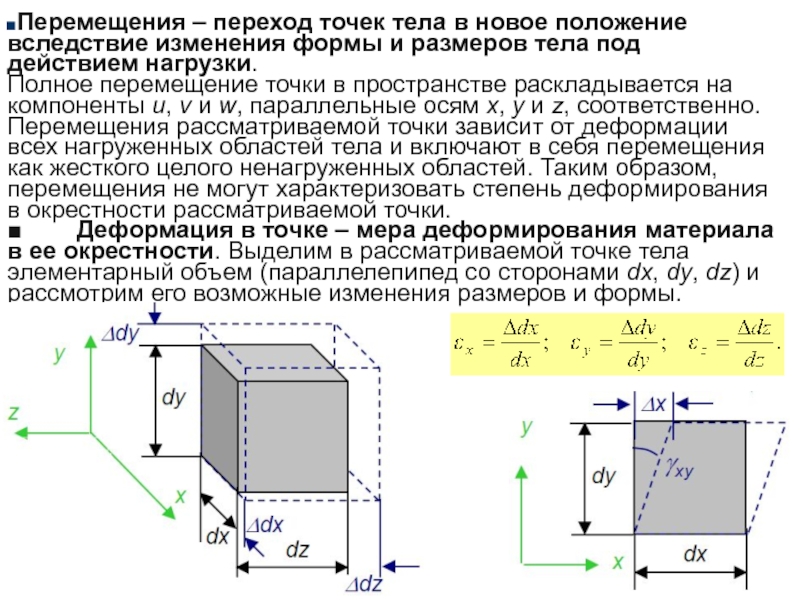
упругости имеют электромагнитную природу.Слайд 11Перемещения – переход точек тела в новое положение вследствие изменения
формы и размеров тела под действием нагрузки.
Полное перемещение точки в
пространстве раскладывается на компоненты u, v и w, параллельные осям x, y и z, соответственно.Перемещения рассматриваемой точки зависит от деформации всех нагруженных областей тела и включают в себя перемещения как жесткого целого ненагруженных областей. Таким образом, перемещения не могут характеризовать степень деформирования в окрестности рассматриваемой точки.
■ Деформация в точке – мера деформирования материала в ее окрестности. Выделим в рассматриваемой точке тела элементарный объем (параллелепипед со сторонами dx, dy, dz) и рассмотрим его возможные изменения размеров и формы.
Слайд 12Кроме линейных деформаций, связанных с изменением размеров линейных элементов возникают
угловые деформации или углы сдвига, связанные с изменением формы. Например,
в плоскости xy могут возникать малые изменения первоначально прямых углов параллелепипеда:Все относительные деформации весьма малы и имеют для реальных материалов порядок ≈10-4-10-3.
В зависимости от того, какие из компонент относительных деформаций
Имеют нулевое значение в рассматриваемой области или для всего тела
Различают следующие простые виды деформаций:
Линейная деформация – εz ≠ 0, углы сдвига равны нулю, остальными
линейными относительными деформациями пренебрегается
(характеризуется абсолютным и относительным удлинением).
Плоская деформация – εz ≠ 0, εx ≠ 0 или εy ≠ 0, остальные относительные
деформации равны нулю (характеризуется абсолютным и относительным
сужением площади поперечного сечения). Эти виды деформаций обычно
реализуются при растяжении-сжатии.
Объемная деформация – εz ≠ 0, εx ≠ 0, εy ≠ 0, углы сдвига равны нулю
(характеризуется абсолютным и относительным изменением объема).
4.Чистый сдвиг – линейные относительные деформации равны нулю, углы
cдвига не равны нулю (характеризуется изменением формы, изменение
объема не происходит). Это вид деформации также возникает при
кручении.
Такие угловые деформации в общем случае могут иметь место во всех трех плоскостях.
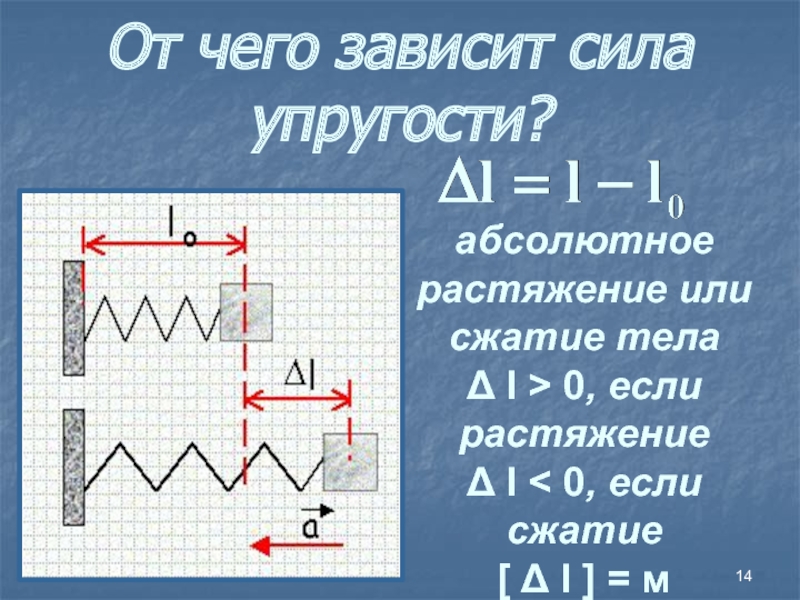
Слайд 14От чего зависит сила упругости?
абсолютное растяжение или сжатие тела
Δ l > 0, если растяжение Δ l < 0, если сжатие Δ l = м
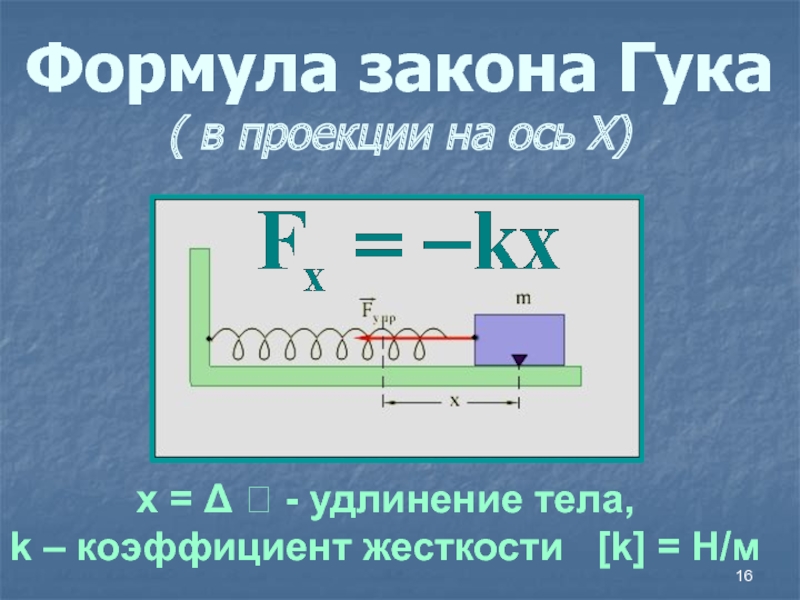
Слайд 16Формула закона Гука
( в проекции на ось Х)
х =
Δ - удлинение тела,
k – коэффициент жесткости k = Н/мСлайд 17Что называется жесткостью тела?
Коэффициент жесткости зависит от формы
и размеров тела, а также от материала.
Он численно равен силе упругости при растяжении тела на 1 м.При действии одной и той же силы на разные пружины они имеют разное абсолютное удлинение (сжатие), т.к. жесткость первой пружины больше жесткости второй (к1 > к2)
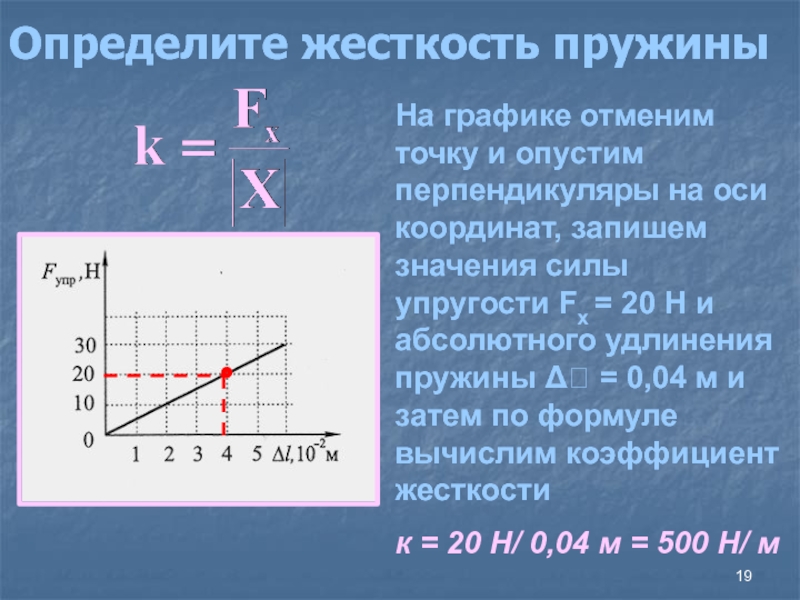
Слайд 19Определите жесткость пружины
На графике отменим точку и опустим перпендикуляры на
оси координат, запишем значения силы упругости Fx = 20 Н
и абсолютного удлинения пружины Δ = 0,04 м и затем по формуле вычислим коэффициент жесткостик = 20 Н/ 0,04 м = 500 Н/ м
Слайд 20Закон Гука для малых упругих деформаций
Сила упругости, возникающая
при деформации тела, прямо пропорциональна его удлинению (сжатию) и направлена
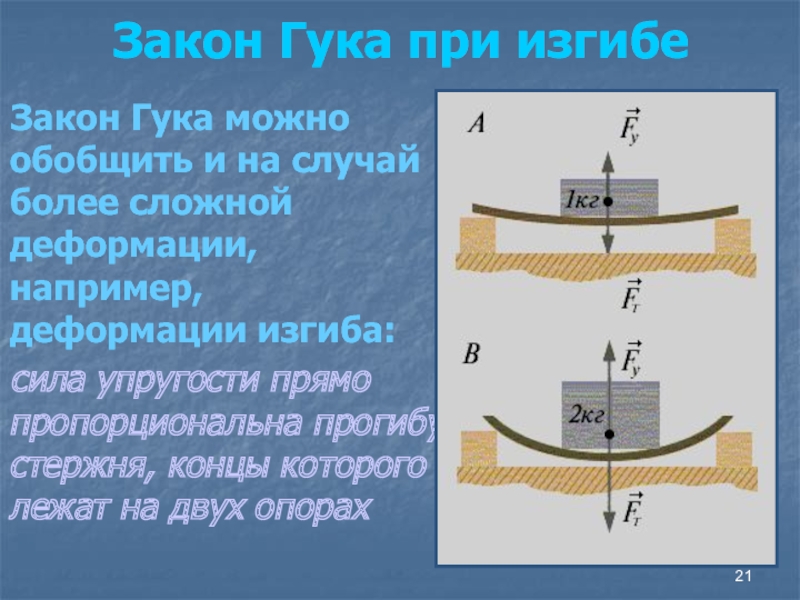
противоположно перемещению частиц тела при деформацииСлайд 21Закон Гука при изгибе
Закон Гука можно обобщить и
на случай более сложной деформации, например, деформации изгиба:
сила
упругости прямо пропорциональна прогибу стержня, концы которого лежат на двух опорахСлайд 23В физике закон Гука принято записывать в другой форме
Для этого введем две новые величины: относительное удлинение (сжатие) –
εи напряжение - σ
Относительное удлинение (сжатие) – это изменение длины тела, отнесенное к единице длины. Оно равно отношению относительного удлинения тела (сжатия) к его первоначальной длине:
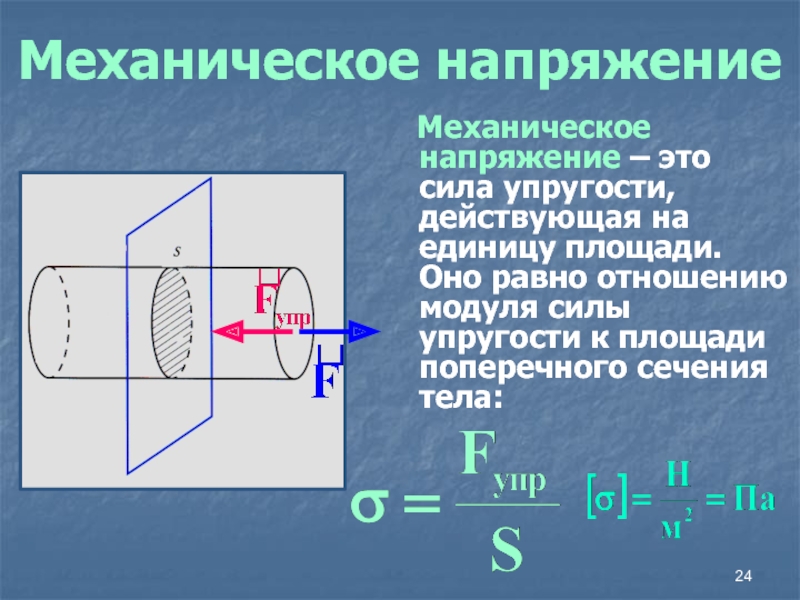
Слайд 24Механическое напряжение
Механическое напряжение – это сила упругости, действующая
на единицу площади. Оно равно отношению модуля силы упругости к
площади поперечного сечения тела:Слайд 25При упругой малой деформации механическое напряжение прямо пропорционально относительному удлинению
(сжатию) тела
где Е – модуль Юнга или модуль упругости, который
измеряется в Па ( Е = σ / ε измеряется в тех же единицах, что напряжение)Слайд 27Модуль упругости - Е
Модуль Юнга зависит только от
свойств материала и не зависит от размеров и формы тела.
Модуль Юнга показывает напряжение, которое необходимо приложить к телу, чтобы удлинить его в 2 раза.Для различных материалов модуль Юнга меняется в широких пределах. Для стали, например, E ≈ 2·1011 Н/м2, а для резины E ≈ 2·106 Н/м2.