Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прогнозирование на основе регрессии. Оценка качества модели
Содержание
- 1. Прогнозирование на основе регрессии. Оценка качества модели
- 2. Корреляционный и регрессионный анализЕсть два самостоятельных процесса2.
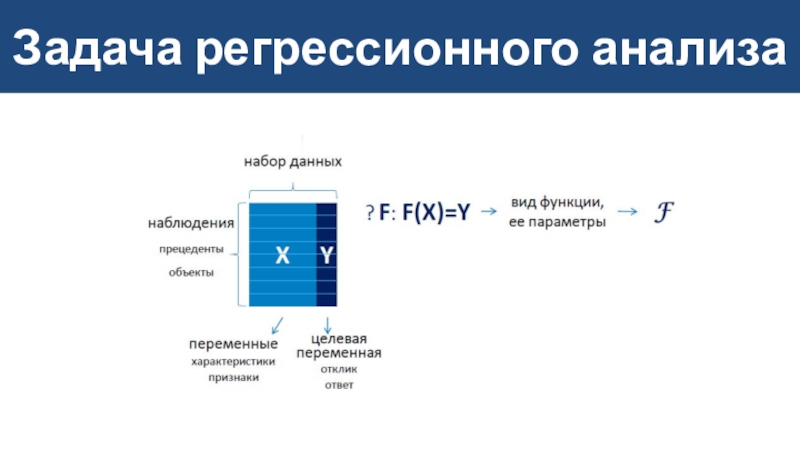
- 3. Задача регрессионного анализа
- 4. Линейная регрессия
- 5. Линейная регрессияПод моделью линейной регрессии будем понимать
- 6. Применение регрессионных моделей1 Для предсказания2 Для исследования
- 7. Остатки регрессии
- 8. RSS (Residual Sum of Squares)
- 9. RSS (Residual Sum of Squares)
- 10. Метод наименьших квадратов
- 11. Метод наименьших квадратов (регрессия на один признак)
- 12. Предобработка данныхВозможно ли уменьшить количество признаков? – применяют методы снижения размерности признакового пространстваПропуски в данных? Выбросы?
- 13. Построение модели регрессии с использованием SAS/STAT1.
- 14. Качественная оценка тесноты связи
- 15. boston.csvCRIM - уровень преступности на душу населения
- 16. Качественная оценка тесноты связи
- 17. Построение модели регрессии с использованием SAS/STAT3.
- 18. Построение модели регрессии с использованием SAS/STAT5.
- 19. Выбор инструментов в SAS/STAT
- 20. Выбор инструментов в SAS/STAT-1
- 21. Выбор инструментов в SAS/STAT Y = f(x1,
- 22. Выбор инструментов в SAS/STAT-2 NONE - не
- 23. Построение модели регрессии с использованием SAS/STAT6.
- 24. Оценка значимости коэффициентов регрессииоценка значимости каждого коэффициента регрессии (t-статистика Стьюдента, p-уровень значимости (
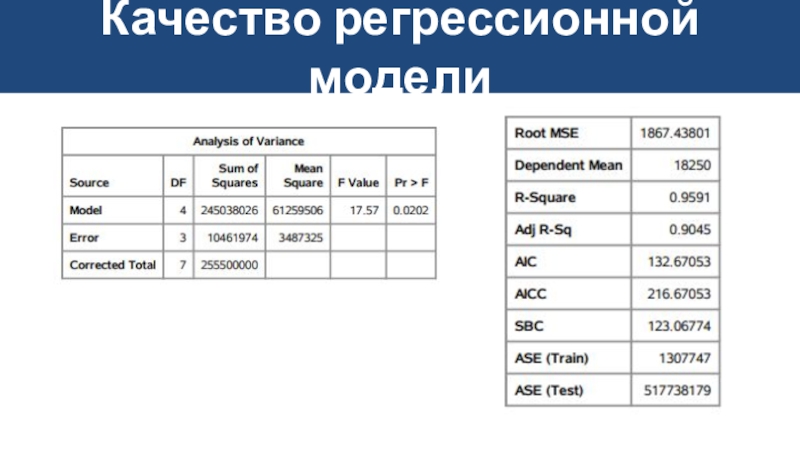
- 25. Качество регрессионной моделиКоэффициент детерминации / скорректированный коэффициент детерминации (>0,75)F-статистика Фишера, p-уровень значимости (
- 26. Качество регрессионной модели
- 27. Качество регрессионной модели
- 28. Качество регрессионной моделиСкорректированный коэффициент детерминацииПроблемы с использованием R2 заключаются
- 29. Качество регрессионной моделиАнализ регрессионных остатковМодель считается качественной,
- 30. Анализ остатков
- 31. Качество регрессионной модели
- 32. Задание 31. На основе индивидуальных данных о
- 33. Скачать презентанцию
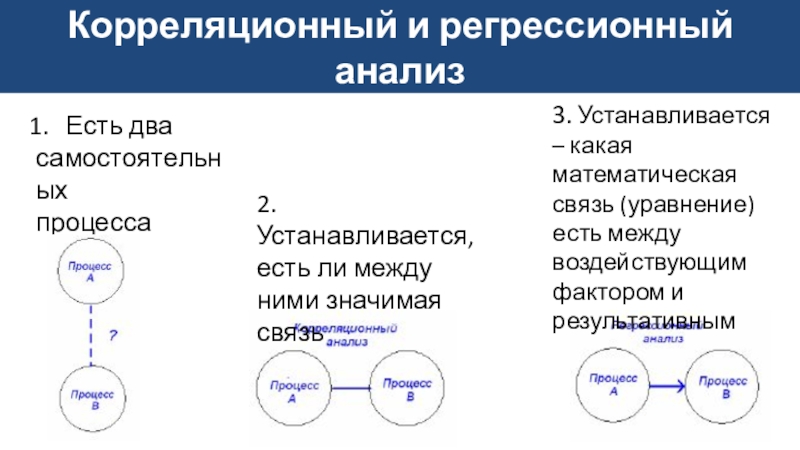
Корреляционный и регрессионный анализЕсть два самостоятельных процесса2. Устанавливается, есть ли между ними значимая связь3. Устанавливается – какая математическая связь (уравнение)есть между воздействующим фактором и результативным
Слайды и текст этой презентации
Слайд 2Корреляционный и регрессионный анализ
Есть два
самостоятельных
процесса
2. Устанавливается, есть ли
между ними значимая связь
между воздействующим фактором и результативнымСлайд 5Линейная регрессия
Под моделью линейной регрессии будем понимать модель вида:
где
y
– объясняемый ряд (выходной параметр, отклик, целевой показатель, зависимая переменная),
x1, …, xk – объясняющие ряды (входные параметры, предикторы, независимые переменные),
e – вектор ошибок модели,
b0, b1, …, bk – коэффициенты регрессии.
Необходимо определить коэффициенты регрессии.
Слайд 12Предобработка данных
Возможно ли уменьшить количество признаков? – применяют методы снижения
размерности признакового пространства
Пропуски в данных?
Выбросы?
Слайд 13Построение модели регрессии
с использованием SAS/STAT
1. Исследовать данные с помощью
утилит Описание данных, Фильтрация данных (при необходимости), Стандартизация данных, Исследование
данных, Сводная статистика2. Установить наличие и характер связи между признаками с помощью утилиты Корреляционный анализ. Предикторы (входные переменные), имеющие сильную взаимную связь – кандидаты на исключение из модели.
(Выявление мультиколлинеарности и возможности снижения размерности признакового пространства)
Слайд 15boston.csv
CRIM - уровень преступности на душу населения по районам
ZN -
доля жилой земли, зонированной для участков более 25 000 кв.
INDUS
- доля неторговых площадей на городCHAS - фиктивная переменная Чарльза (= 1, если тракт ограничивает реку; 0 в противном случае)
NOX - концентрация оксидов азота (частей на 10 миллионов)
RM - среднее количество комнат в доме
AGE - доля владельцев домов, построенных до 1940 года
DIS - взвешенные расстояния до пяти бостонских центров занятсти
RAD - индекс доступности к радиальным магистралям
TAX - ставка налога на имущество на полную стоимость за 10 000 долл.
PTRATIO - соотношение учеников и учителей по районам
Black - доля чернокожих по районам
LSTAT - % населения низкого статуса
MEDV - средняя стоимость домов, занимаемых владельцами, в 1000 долл.
Слайд 17Построение модели регрессии
с использованием SAS/STAT
3. Разбиение выборки (обучающая и
тестовая)
4. Настройка ролей (зависимая и независимые переменные)
Слайд 18Построение модели регрессии
с использованием SAS/STAT
5. Выбор инструментов моделирования в
SAS/STAT:
выбор вида модели и формирование математической конструкции модели с помощью
Конструктора эффектов модели;выбор алгоритмов отбора признаков в модель
Слайд 21Выбор инструментов в SAS/STAT
Y = f(x1, x2, x3, x4,
x5…x12)
Y =b1x1 + b2x2+ b3x3+ b4x4…+ b12x12 – линейная модель
Y
=b1x12 + b2x2+ b3х1x3+ b4x42…+ b12x9x12 – нелинейная модельY =b1x1x2 + b2x23+ b3x3+ b4x4…+ b12x12 – нелинейная модель
…
В Конструкторе эффектов модели можно формировать различные математические модели для одного и того же набора входных/выходных переменных
Слайд 22Выбор инструментов в SAS/STAT-2
NONE - не выполняет выбор переменных,
использует полную модель
FORWARD - использует алгоритм прямого выбора для выбора
переменных. Этот метод начинается с отсутствия переменных в модели и добавляет переменные одну за другой в модель. На каждом шаге добавляемая переменная лучше всего подходит для модели. BACKWARD - использует алгоритм обратного исключения для выбора переменных (начинается с полной модели и исключает переменные по одной из модели). На каждом шаге переменная, которая вносит наименьший вклад в модель, удаляется
LASSO
LAR (использует регрессию наименьшего угла)
MAXR - использует максимальное улучшение R-квадрата для выбора моделей
MINR - использует минимальное улучшение R-квадрата для выбора моделей.
RSQUARE
ADJRSQ
Слайд 23Построение модели регрессии
с использованием SAS/STAT
6. Оценка качества модели
7. Сравнение
моделей и выбор наилучшей модели по заданному критерию
Слайд 24Оценка значимости коэффициентов регрессии
оценка значимости каждого коэффициента регрессии (t-статистика Стьюдента,
p-уровень значимости (
Слайд 25Качество регрессионной модели
Коэффициент детерминации / скорректированный коэффициент детерминации (>0,75)
F-статистика Фишера,
p-уровень значимости (
ошибка (MAE)Среднее квадратичное отклонение (MSE) Среднеквадратичная ошибка (RMSE) ( min)
Слайд 28Качество регрессионной модели
Скорректированный коэффициент детерминации
Проблемы с использованием R2 заключаются в том, что
его значение не уменьшается при добавлении в уравнение факторов, сколь
плохи бы они ни были. Поэтому сравнивать модели с разным количеством факторов, используя R2, не имеет смысла. Для этого используется скорректированный коэффициент детерминации Adj R2:где k – число факторов, включенных в модель.
Коэффициент Adj R2 также принимает значения от 0 до 1, но никогда не будет больше, чем значение R2.
Слайд 29Качество регрессионной модели
Анализ регрессионных остатков
Модель считается качественной, если остатки модели
не коррелируют между собой, то есть являются независимыми нормально распределенными
случайными величинами с нулевым средним, и в их значениях должен отсутствовать тренд. Анализ регрессионных остатков - это процесс проверки выполнения этих условий. В противном случае имеет место постоянное однонаправленное воздействие на объясняемую переменную не учтённых в модели факторов. Это влияет на качество оценок модели, делая их неэффективными.http://www.machinelearning.ru/wiki/index.php?title=%D0%90%D0%BD%D0%B0%D0%BB%D0%B8%D0%B7_%D1%80%D0%B5%D0%B3%D1%80%D0%B5%D1%81%D1%81%D0%B8%D0%BE%D0%BD%D0%BD%D1%8B%D1%85_%D0%BE%D1%81%D1%82%D0%B0%D1%82%D0%BA%D0%BE%D0%B2
Слайд 32Задание 3
1. На основе индивидуальных данных о недвижимости (файл “boston.csv”)
проведите оценку основных статистических характеристик набора данных с использованием SAS
Studio.2. Исследуйте набор данных на наличие мультиколлинеарности.
3. С помощью корреляционного анализа ответьте на вопросы: «Можно ли снизить размерность признакового пространства? Целесообразно ли это? Почему?» Обоснуйте свой ответ.
4. Протестируйте различные методы отбора переменных для линейной и нелинейной модели. Эффекты моделей задайте самостоятельно с использованием Конструктора эффектов модели. Для пошаговых методов отбора переменных исследуйте влияние порогов для p-value для входных (включаемых в регрессию) и выходных (исключаемых из регрессии) переменных. Сравните построенные модели по критериям оценки качества модели, рассмотренным в данной презентации. Результаты сравнения сведите в таблицу.
5. Выберите «наилучшую» модель на основе проведенных исследований.