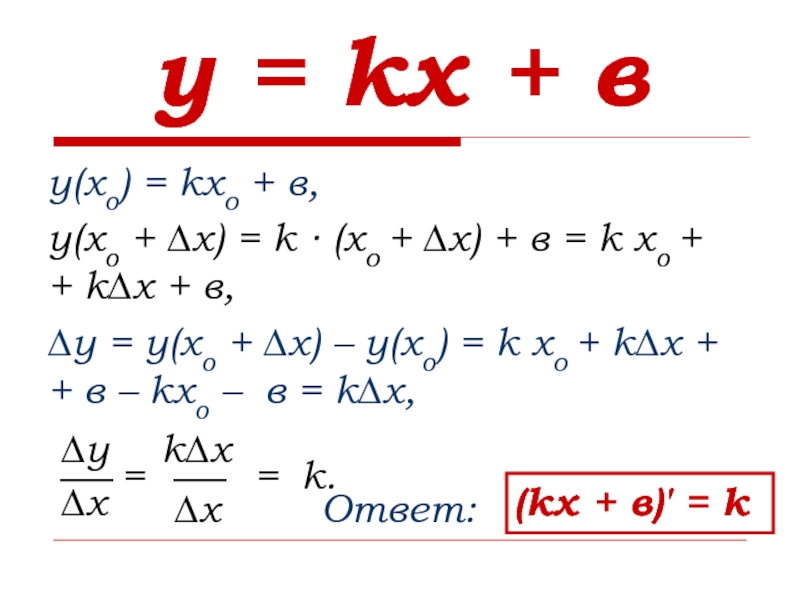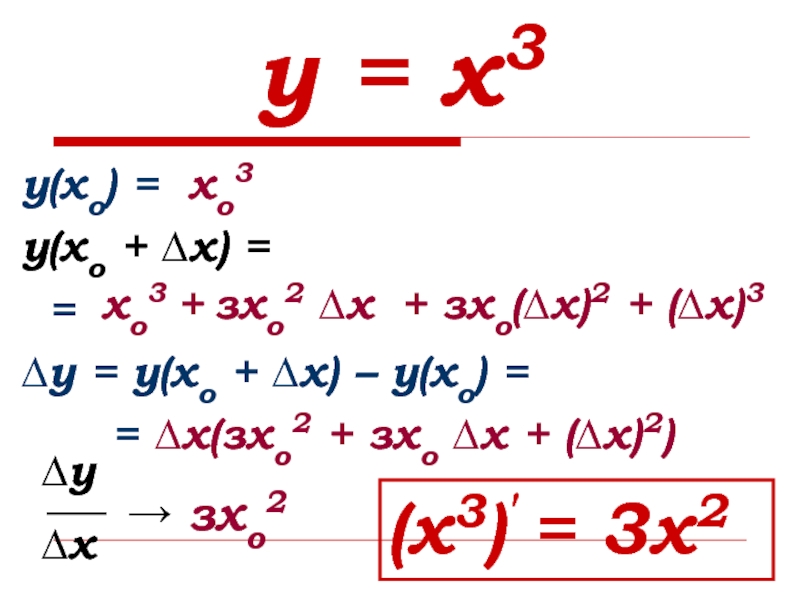Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Производная функции
Содержание
- 1. Производная функции
- 2. Проблемный вопросМожно ли находить производные, не используя определение?Существуют ли более удобные способы?
- 3. Цели и задачи Научиться находить производные
- 4. Приращение функции и аргумента х =
- 5. Определение производной f ′(xо) – число
- 6. у = kх + ву(хо) = kхо
- 7. у = х2у(хо) = хо2,у(хо + ∆х)
- 8. у = х3у(хо) =у(хо + ∆х) =
- 9. Вывод Нужны формулы:быстро,удобно.(kх + в)′ = k(х2)′
- 10. Найди производную!(х7)′(5х3)′(- 7х9)′(0,5х-3)′(9х + 16)′(7 – 4х)′7. 8.
- 11. Проверь себя! 7х6 15х2 – 63х8
- 12. Используемая литератураАлгебра и начала анализа: Учеб. для
- 13. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Проблемный вопрос
Можно ли находить производные, не используя определение?
Существуют ли более
удобные способы?
Слайд 3Цели и задачи
Научиться находить производные элементарных функций, при
этом:
повторить
определения приращения функции и приращения аргумента;
определение производной функции в точке
хо;алгоритм нахождения производной.
Слайд 4Приращение функции
и аргумента
х = х – хо –
приращение аргумента
f(х) = f(х) – f(хо)
f(х) = f (хо
+ х ) – f(хо) приращение функции
–
Найдите f, если f(х) = х2, хо = 1, ∆х = 0,5
Решение: f(хо) = f(1) = 12 = 1,
f (хо + х ) = f(1 + 0,5) = f(1,5) = 1,52 = 2,25,
f = 2,25 – 1 = 1,25.
Ответ: f = 1,25
изменение
Слайд 5Определение производной
f ′(xо) –
число
Алгоритм:
1) ∆х,
хо;
2) ∆f = f (хо + х ) – f(хо);
3)
при ∆х → 0.,
Слайд 6у = kх + в
у(хо) = kхо + в,
у(хо +
∆х) = k ∙ (хо + ∆х) + в =
k хо + + k∆х + в,∆у = у(хо + ∆х) – у(хо) = k хо + k∆х + + в – kхо – в = k∆х,
(kх + в)′ = k
Ответ:
=
k∆х
=
k.
∆x
∆x
∆y
Слайд 7у = х2
у(хо) = хо2,
у(хо + ∆х) = (хо +
∆х)2= хо2 + 2 хо ∆х + (∆х)2,
∆у = у(хо
+ ∆х) – у(хо) = хо2 + 2 хо ∆х + + (∆х)2 – хо2 = 2 хо ∆х + (∆х)2 = ∆х(2хо + ∆х), ∆у
∆х
=
∆х (2хо + ∆х)
∆х
=
2хо + ∆х
→
2хо
при ∆х → 0
Ответ:
(х2)′ = 2х
Слайд 8у = х3
у(хо) =
у(хо + ∆х) =
=
∆у = у(хо + ∆х) – у(хо) =
=хо3
∆х(зхо2 + зхо ∆х + (∆х)2)
хо3 + зхо2 ∆х + зхо(∆х)2 + (∆х)3
∆у
∆х
зхо2
→
(х3)′ = 3х2