Слайд 1ПРОСТРАНСТВЕННАЯ ПРОИЗВОЛЬНАЯ СИСТЕМА СИЛ
Кафедра теоретической механики и сопротивления материалов
Методические указания
по теоретической механике для практических занятий и самостоятельной работы студентов
2 курса инженерных специальностей
Владивосток
2011
Составил В. Г. Непейвода
ФЕДЕРАЛЬНОЕ АГЕНТСТВО МОРСКОГО И РЕЧНОГО ТРАНСПОРТА
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Морской государственный университет им. адм. Г. И. Невельского
Слайд 2 1. Общие положения
Содержание
2. Момент силы относительно
оси
3. Тренировочные задания
4. Применение теоремы Вариньона
5. Примеры решения задач
6. Задачи для самостоятельного решения
Слайд 31. Общие положения
Произвольной пространственной называется система сил, линии
действия которых расположены произвольно в пространстве, рис. 1.
Слайд 4
Произвольная пространственная система сил может быть приведена к
силе, равной главному вектору и приложенной в произвольном центре приведения
сил О, и к паре с моментом, равным главному моменту системы сил относительно центра приведения, рис. 2.
Слайд 5 При равновесии тела под действием произвольной пространственной системы
сил выполняются векторные условия:
Из векторных условий равновесия следуют
уравнения равновесия:
Таким образом, для того, чтобы тело под действием пространственной произвольной системы сил находилось в равновесии, необходимо и достаточно, чтобы суммы проекций сил на координатные оси x, y, z и суммы моментов сил относительно этих осей равнялись нулю.
Слайд 62. Момент силы относительно оси
Момент силы относительно оси
характеризует враща-тельную способность силы относительно выбранной оси, явля-ется алгебраической величиной
и определяется в следующей последовательности.
1. Силу необходимо спроецировать на плоскость, перпендикулярную данной оси, и определить полученную при этом проекцию.
2. Найти плечо полученной проекции относительно точки пересечения плоскости с осью и определить его.
3. Умножить проекцию на плечо и приписать полученному произведению знак «+» если при взгляде с положительного направления данной оси вращения видно, что сила вызывает вращение тела против хода часовой стрелки. В противном случае моменту силы приписывается знак «–».
Слайд 7 Момент силы относительно оси равен нулю в следующих
случаях:
1) сила параллельна оси;
2) сила и ось лежат в одной
плоскости.
Пример 1. Найдём момент силы относительно оси z, рис. 3.
Слайд 8строим плоскость, перпендикулярную оси, которая составляет с плоскостью угол α;
Слайд 92) проецируем силу на эту плоскость;
Слайд 10 3) из точки пересечения оси z с плоскостью
(точка О) на линию действия проекции силы FQ построим перпендикуляр
h. Этот перпендикуляр является плечом проекции относитель-но точки О.
Слайд 11 4) найдём величину момента силы относительно оси z;
Слайд 12 5) определяем знак момента.
Момента силы
имеет знак (+), если с положительного конца оси поворот, который
стремится совершить проекция силы на плоскость Q виден против часовой стрелки, и знак (-),если по ходу часовой стрелки. Следовательно момент силы на рис. 6 равен:
Слайд 13 Пример 2. На вал с маховиком, радиус которого
равен r (рис. 4), действует сила . Требуется определить моменты
этой силы относительно каждой из координатных осей Oxyz.
Слайд 14 Для определения момента силы относительно оси x построим
проекцию вала и силы на плоскость, перпендикуляр-ную этой оси, т.
е. на плоскость zOy, рис. 5.
Слайд 15
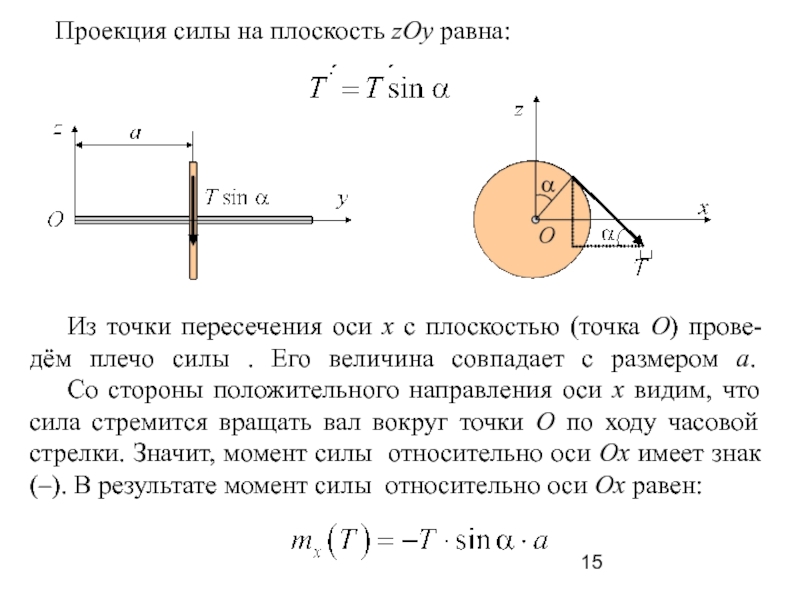
Проекция силы на плоскость zOy равна:
Из
точки пересечения оси x с плоскостью (точка О) прове-дём плечо
силы . Его величина совпадает с размером а.
Со стороны положительного направления оси x видим, что сила стремится вращать вал вокруг точки О по ходу часовой стрелки. Значит, момент силы относительно оси Оx имеет знак (–). В результате момент силы относительно оси Оx равен:
Слайд 16 Чтобы определить момент рассматриваемой силы относительно оси y,
построим проекцию вала и силы на плоскость, перпендикулярную оси Oy
– плоскость xOz, рис. 6. Из точки пересечения оси Oy с этой плоскостью (точки О) на линию действия проекции силы восстановим перпендикуляр. По величине и направлению он совпадает с радиусом маховика при любом угле α.
Слайд 17 Со стороны положительного направления оси y видно, что
проекция силы стремится создать вращение вала относительно точки О против
хода часовой стрелки. Поэтому момент силы относительно оси y равен:
Из рисунка видим, что плечом силы T является радиус маховика.
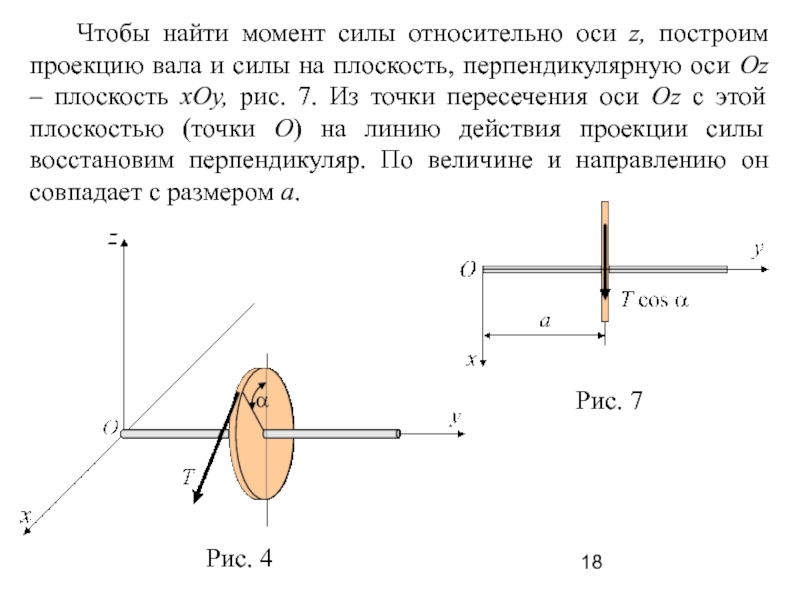
Слайд 18 Чтобы найти момент силы относительно оси z, построим
проекцию вала и силы на плоскость, перпендикулярную оси Oz –
плоскость xOy, рис. 7. Из точки пересечения оси Oz с этой плоскостью (точки О) на линию действия проекции силы восстановим перпендикуляр. По величине и направлению он совпадает с размером а.
Слайд 19 Со стороны положительного направления оси z видим, что
проекция силы стремится создать вращение вала относительно точки О по
ходу часовой стрелки. Поэтому момент силы T относительно оси Oz имеет знак «–» и равен
Слайд 203. Тренировочные задания
Задание 1. К параллелепипеду на рис.
8, стороны которого равны a, b и c, приложены силы
. Значения углов α, β, заданы.
Запишите моменты этих сил относительно осей x, y, z, и сравните свои результаты с правильными ответами, приведенными ниже.
Слайд 25 Задание 2. Ось коленчатого вала (рис. 9) расположена
вдоль оси x и удерживается в равновесии реакциями подшипников. Прямоугольное
колено DЕGF образует с плоскостью xАy угол ϕ. На колено вала в точке С действует сила P, отклонённая от вертикали на угол α в плоскости, перпендикулярной оси x, пара сил с моментом m, плоскость действия которой перпендикулярна оси x. Считая расстояния AD, DE, EC, CG, GF и FB заданными; Запишите алгебраические суммы моментов всех сил относительно осей x, y, z.
Слайд 26 Сравните свои результаты с ответами.
Сумма моментов
сил относительно оси x = ?
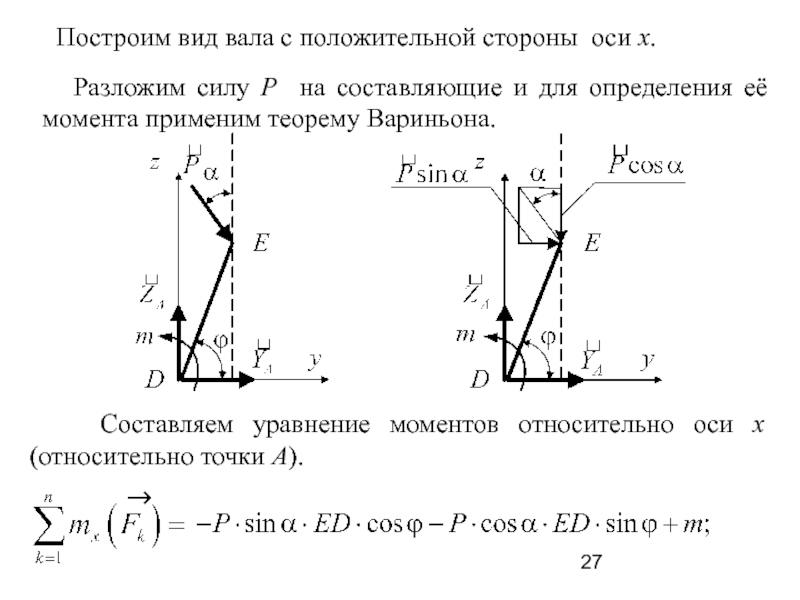
Слайд 27 Построим вид вала с положительной стороны оси x.
Разложим силу P на составляющие и для определения её
момента применим теорему Вариньона.
Составляем уравнение моментов относительно оси x (относительно точки А).
Слайд 29
Сумма моментов сил относительно оси y = ?
Слайд 30 Сумма моментов сил относительно оси z = ?
Слайд 314. Применение теоремы Вариньона
Если известны углы наклона
силы к плоскостям коорди-натных осей, то для вычисления момента силы
относительно осей рекомендуется применять теорему Вариньона.
Применительно к оси теорема читается так: момент равно-действующей силы относительно какой-либо оси равен алгебра-ической сумме моментов её составляющих относительно той же оси.
Теорема Вариньона применяется в следующей последователь-ности.
1. Сила раскладывается на составляющие по координатным осям. В общем случае таких составляющих будет три: по x, по y и по z. В частном случае их может быть две.
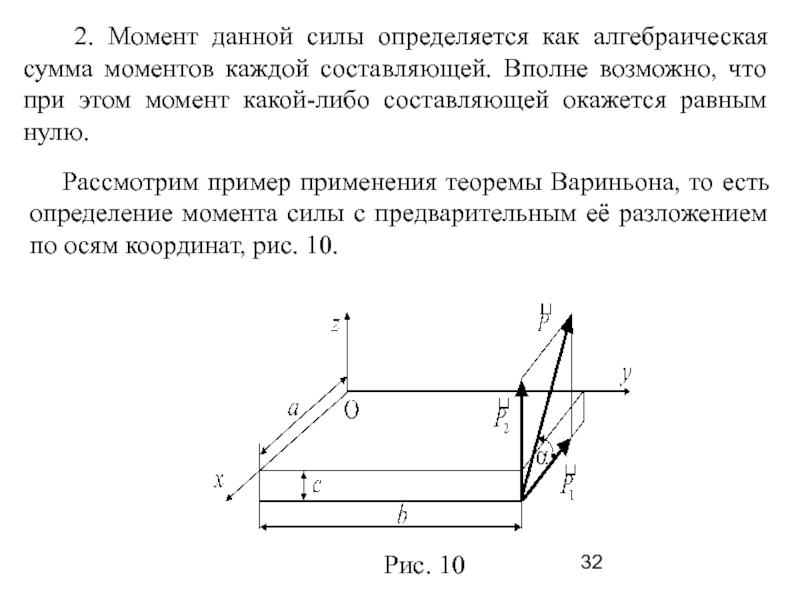
Слайд 32 2. Момент данной силы определяется как алгебраическая сумма
моментов каждой составляющей. Вполне возможно, что при этом момент какой-либо
составляющей окажется равным нулю.
Рассмотрим пример применения теоремы Вариньона, то есть определение момента силы с предварительным её разложением по осям координат, рис. 10.
Слайд 33
где
.
По теореме Вариньона
Находим моменты составляющих:
Слайд 36 При решении задач будем придерживаться следующего плана.
1. Выбрать тело (конструкцию, узел конструкции), равно-весие которого необходимо рассмотреть,
чтобы найти неиз-вестные величины.
2. Показать активные силы, действующие на тело, а также известные силы реакций связей, если такие есть.
3. Применить метод освобождения от связей и показать реакции связей, подлежащие определению.
4. Составить уравнения равновесия.
5. Решить систему уравнений способом подстановки или с использованием стандартных программ, установленных на персональном компьютере.
5. Примеры решения задач
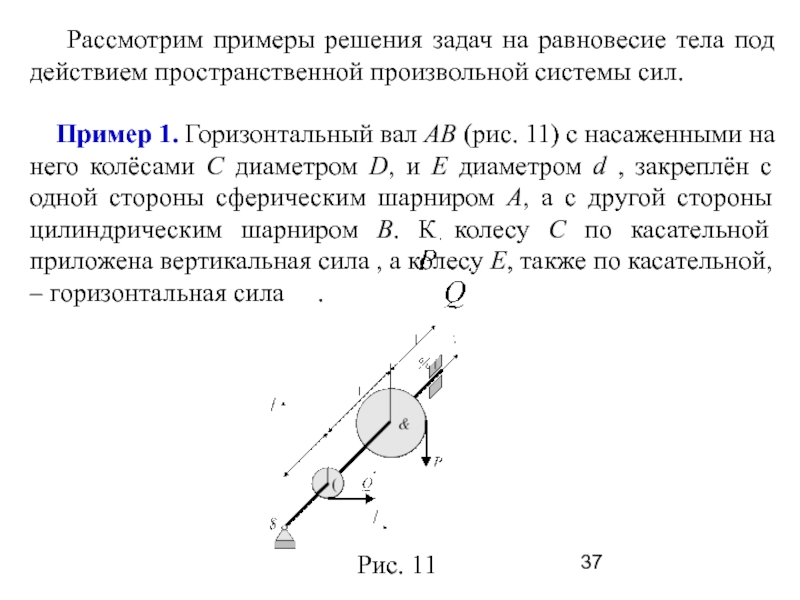
Слайд 37 Рассмотрим примеры решения задач на равновесие тела под
действием пространственной произвольной системы сил.
Слайд 39Решение
Дано: d = 0,2 м.; D = 1
м.; Р=15 кН. Определить Q, реакции опор А и В.
Чтобы определить реакции опор, рассмотрим равновесие вала АВ.
1. Равновесие какого тела необходимо рассмотреть, чтобы найти неизвестные силы?
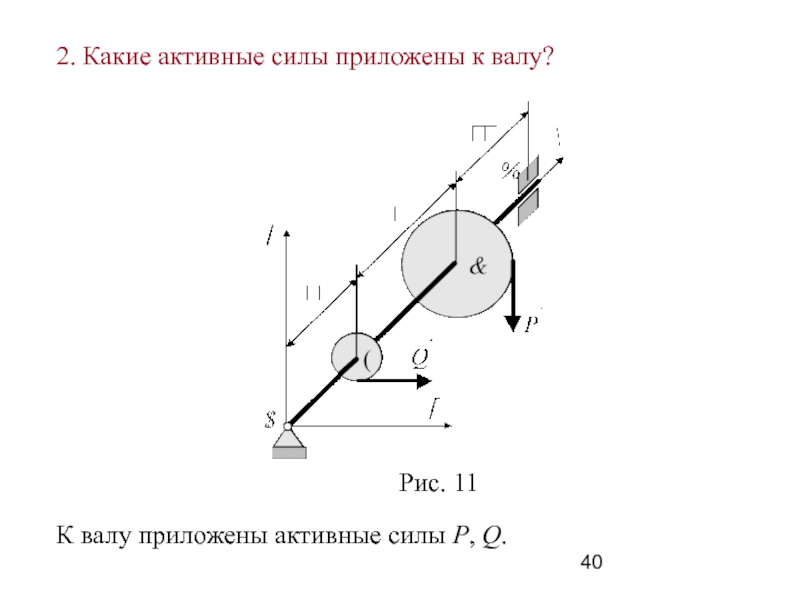
Слайд 40 К валу приложены активные силы P, Q.
2. Какие активные силы приложены к валу?
Слайд 41 3. Как называются связи, действующие на вал?
Вал имеет две связи: сферический шарнир А и цилиндричес-кий шарнир
B.
Слайд 42 5. Как направлена сила реакции сферического шарнира A?
Cила реакции сферического шарнира представляет собой вектор, направленный
произвольно в пространстве, линия действия которого проходит через центр шарнира. На практике вектор раскладывается на три составляющие, направленные по координатным осям x, y, z.
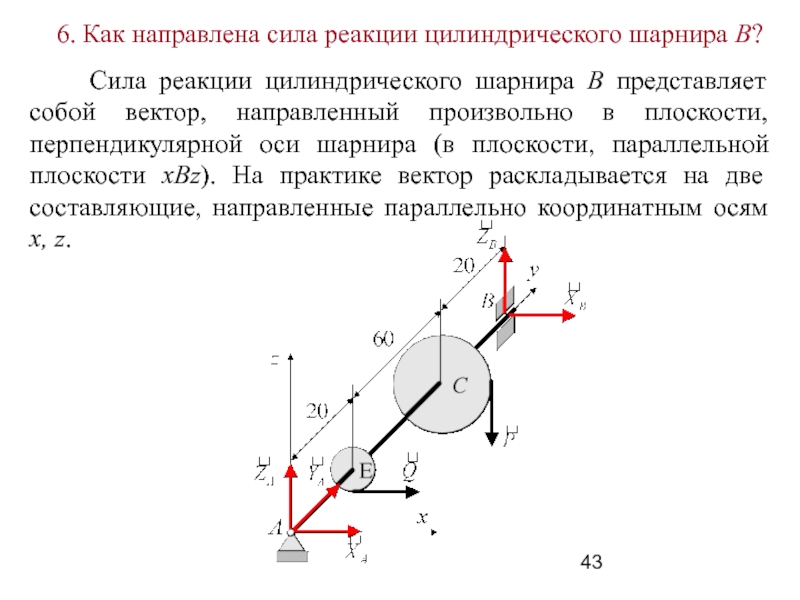
Слайд 43 6. Как направлена сила реакции цилиндрического шарнира В?
Cила реакции цилиндрического шарнира В представляет собой вектор,
направленный произвольно в плоскости, перпендикулярной оси шарнира (в плоскости, параллельной плоскости xВz). На практике вектор раскладывается на две составляющие, направленные параллельно координатным осям x, z.
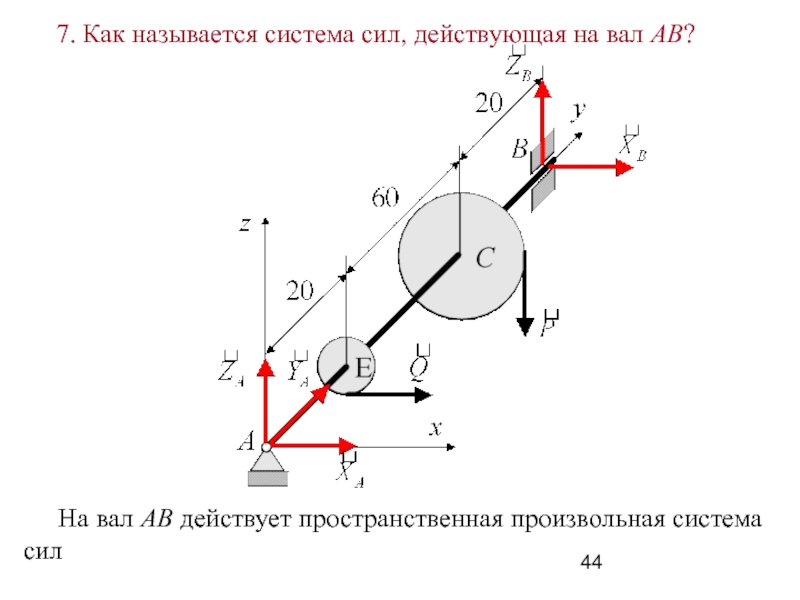
Слайд 44 7. Как называется система сил, действующая на вал
AB?
На вал АВ действует пространственная произвольная система
сил
Слайд 45 8. Какие уравнения равновесия можно составить для прос-транственной
произвольной системы сил?
Для пространственной произвольной системы сил можно составить
шесть уравнений:
Слайд 46 Составьте первое уравнение:
Составьте второе уравнение:
Составьте третье уравнение?
Слайд 47 Составьте четвёртое уравнение.
Составьте пятое уравнение.
Составьте шестое уравнение.
Слайд 48 Находим неизвестные силы из уравнений (1) – (6):
из (2): YА = 0;
Слайд 49 Знак «минус» у ХА и ХВ означает, что
направления этих реакций противоположны направлениям, указанным на расчётной схеме.
Слайд 50 1. Коленчатый вал АВ расположен в горизонтальной плоскости.
Нагружен силой F и моментом М, которые действуют в плоскостях,
параллельных плоскости xАz, рис. 16.
Определить силу F и реакции подшипников А и В, если известно, что а = в = 0,2 м; с = 0,4 м, d = 0,1 м, α = 30о, М = 6 Нм.
6. Задачи для самостоятельного решения
Ответ:
Слайд 51 2. Коленчатый вал АВ расположен в горизонтальной плоскости.
Имеет диск D, плоскость которого перпендикулярна АВ. Удерживается в равновесии
силами Р и Т, также расположенными в плоскостях, перпендикулярных АВ. Найти реакции подшипников А и В и силу , если известно, что P = 10 Н, r = 0,2 м, α = 30° и размеры показаны на рисунке в метрах.
Ответ:
Слайд 52 3. Прямоугольная плита весом Р укреплена в горизонтальном
положении с помощью шарнира А, стержней CN и СК и
троса BS. В точке В к плите подвешен груз М весом Q, рис. 15.
Пренебрегая весом стержней и троса, считая все соединения шарнирными, определить реакцию шарнира А, усилия в стержнях и натяжение троса, если P = 100 H, Q = 50 Н, CD = 3 м, CB = 4 м, CE = 5 м, ∠ SBD = 45o.
Слайд 53 4. Дано: P = 100 H, Q =
50 Н, CD = 3 м, CB = 4 м,
CE = 5 м, ∠ SBD = 45o.
Определить реакцию шарнира А, усилия в стержнях NC и CK, натяжение троса BS.
Ответ:
Слайд 54 5. Горизонтальный вал АВ имеет два шкива С
и D ремённой передачи, причём м. Натяжение ремней шкива С,
(Т1 и t1) – горизонтальны, причём Т1 = 2t1 = 5 кН. Натяжения ремня шкива D образуют с вертикалью угол α=30° и имеют величины Т2 и t2, причём t2 = 0,5 Т2.
Ответ: