Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Прямая м наклонная призма
Содержание
- 1. Прямая м наклонная призма
- 2. РазминкаПостарайтесь ответить на вопросы, прежде, чем появятся ответы.После ответов запишите формулы, начертите многоугольники.
- 3. Устная разминка1. Прямоугольный треугольник 1. Чему
- 4. 3. Прямоугольник 1.Чему равна площадь
- 5. 5. Ромб 1. Чему равна S ромба?
- 6. 7. Трапеция . Чему равна площадь трапеции?
- 7. ГАПОУ СО « Талицкий лесотехнический колледж
- 8. Термин “призма” греческого происхождения и буквально означает
- 9. Призма обозначается всеми вершинами(АВСДA1B1C1D1)
- 10. Проверим теорему Эйлера: 1.Команда «Параллелепипед»-треугольная призма;
- 11. Проверим теорему Эйлера: 1.Команда «Параллелепипед»-треугольная призма;
- 12. Призма называется прямой, если ее боковые ребра
- 13. Площадь полной поверхности четырехугольной призмы
- 14. S =а*в ;где
- 15. Площадь полной поверхности треугольной призмыВ основаниях находятся
- 16. Площадь полной поверхности
- 17. Диагональные сечения призмы Диагональю призмы
- 18. Решение задач
- 19. Решение
- 20. Здания-призмы
- 21. Куб в архитектуре. В Роттердаме —
- 22. ПризмаВидыПлощадьОпределениеОбозначенияЭлементыВ зависимости от перпендикулярности боковых граней к
- 23. Практическая часть2.Определите количество граней, вершин и рёбер
- 24. Практическая часть 2. Определите количество граней,
- 25. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Прямая м наклонная призма
Задание:
1.Изучить материал
2.Составить опорный конспект
3. Выполнить практическое
задание по своим вариантам.
Слайд 2Разминка
Постарайтесь ответить на вопросы, прежде, чем появятся ответы.
После ответов запишите
формулы, начертите многоугольники.
Слайд 3 Устная разминка
1. Прямоугольный треугольник
1. Чему равен угол
С?
ответ: 90 градусов
2. Сумма углов треугольника?
ответ: 180 градусов
3. Чему равна
площадь прямоуг.треугольника?ответ:Sтр=1/2 a*b;
2. Косоугольный треугольник
Чему равна площадь косоугольного треугольника?
ответ(формула Герона): S тр = √ р .( р-а ).(р-в).( р-с); р-полупериметр, р=1/2(а+в+с)
h
c
A
B
C
a
b
A
B
C
b
a
c
h
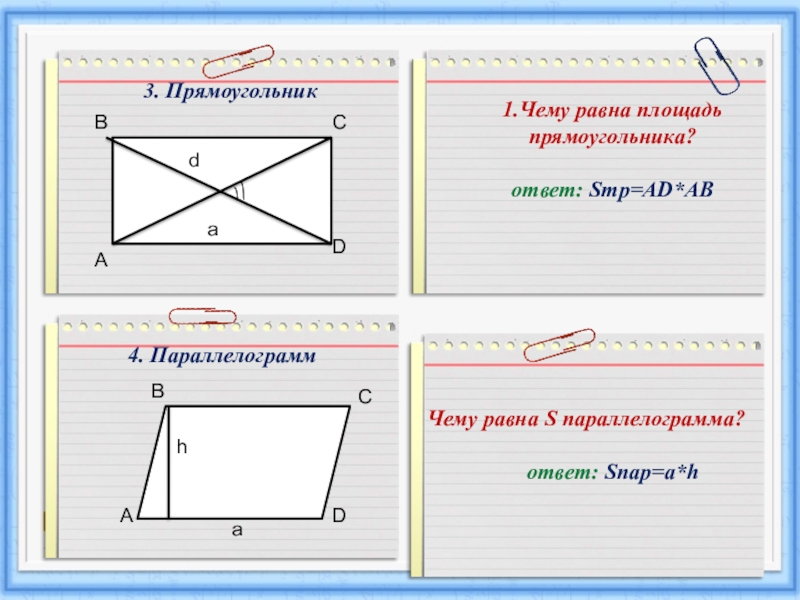
Слайд 4 3. Прямоугольник
1.Чему равна площадь
прямоугольника?
ответ: Sтр=AD*AB
4. Параллелограмм
Чему равна S параллелограмма?
ответ: Sпар=a*h
A
B
C
D
d
a
A
B
C
D
h
a
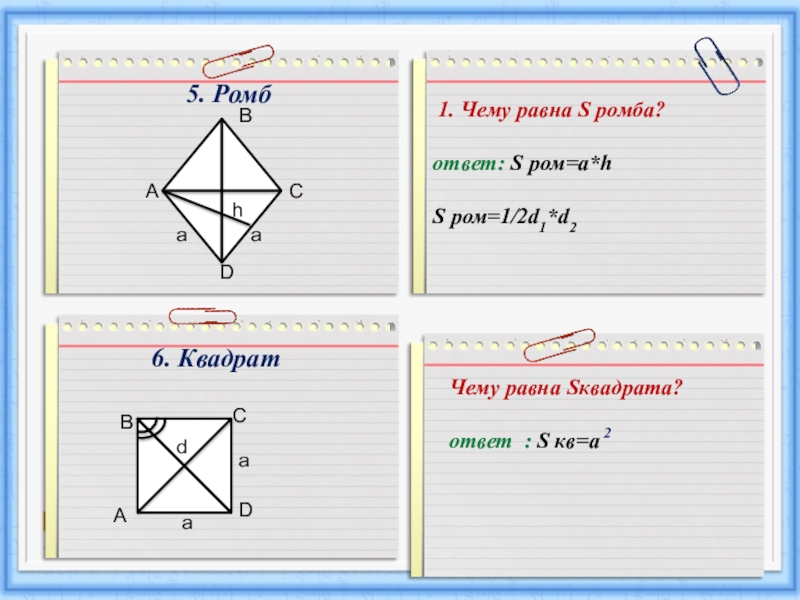
Слайд 55. Ромб
1. Чему равна S ромба?
ответ: S ром=a*h
S ром=1/2d1*d2
6. Квадрат
Чему равна Sквадрата?
ответ : S кв=а
2
A
C
B
D
h
a
a
A
B
C
D
d
a
a
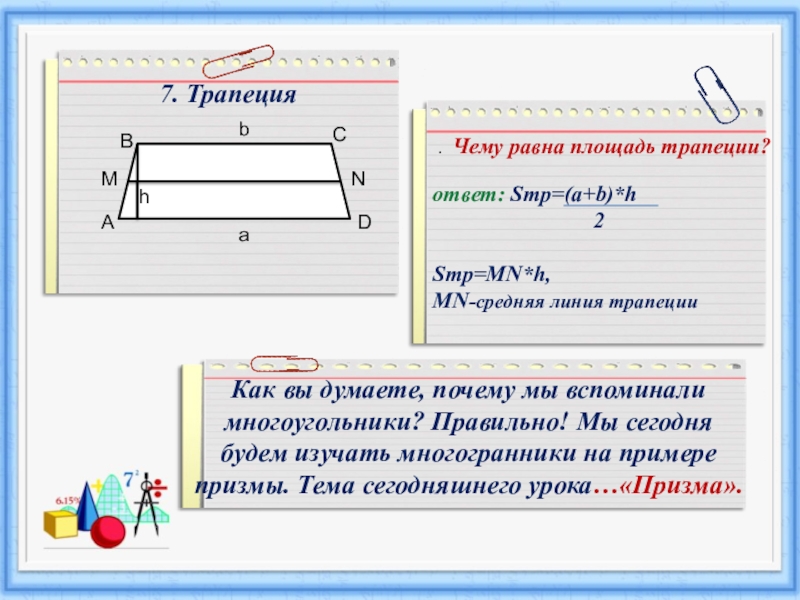
Слайд 67. Трапеция
. Чему равна площадь трапеции?
ответ: Sтр=(a+b)*h
2
Sтр=MN*h, MN-средняя линия трапеции
Как вы думаете, почему мы вспоминали многоугольники? Правильно! Мы сегодня будем изучать многогранники на примере призмы. Тема сегодняшнего урока…«Призма».
A
B
C
D
M
N
b
a
h
Слайд 7ГАПОУ СО « Талицкий лесотехнический колледж
имени Н.И.Кузнецова»
Выполнила Кудина Л.В. преподаватель математики
Талица
Многогранники Тема:«Призма»
Слайд 8Термин “призма” греческого происхождения и буквально означает “отпиленное”
Призма –это тело, ограниченное многогранной поверхностью, две грани которой n – угольники, а остальные n – параллелограммы.
Слайд 9Призма обозначается всеми вершинами(АВСДA1B1C1D1)
или двумя вершинами, не лежащими на одной грани (например А с1 )
Многоугольники, ограничивающие призму, называются гранями (например А А1B1В), их стороны (например АА1 )-ребрами, а вершины( например А, A1)-вершинами призмы. Призмы различаются по числу граней (например трехгранная, четырехгранная, пятигранная…). Полезно знать формулу Эйлера n+s-t=2; где п-число граней, s-число вершин, t-число ребер.
Слайд 10Проверим теорему Эйлера:
1.Команда «Параллелепипед»-треугольная призма;
2.Команда «Призма»- четырехугольная призма; 3.Команда «Пирамида»-пятиугольная призма; 4.Команда «Куб»-шестиугольная призма .
Формула Эйлера: n+s-t=2; где п-число граней, s-число вершин, t-число ребер.
Слайд 11Проверим теорему Эйлера:
1.Команда «Параллелепипед»-треугольная призма; ( 5+6-9=2)
2.Команда «Призма»- четырехугольная призма; (6+8-12=2) 3.Команда «Пирамида»-пятиугольная призма; (7+10-15=2) 4.Команда «Куб»-шестиугольная призма. . (8+12-18=2) .
Слайд 12Призма называется прямой, если ее боковые ребра перпендикулярны плоскости оснований.
Непрямая
призма называется
наклонной.A
B
C
C1
B1
A1
Прямая призма называется правильной, если в ее основании лежит правильный многоугольник.
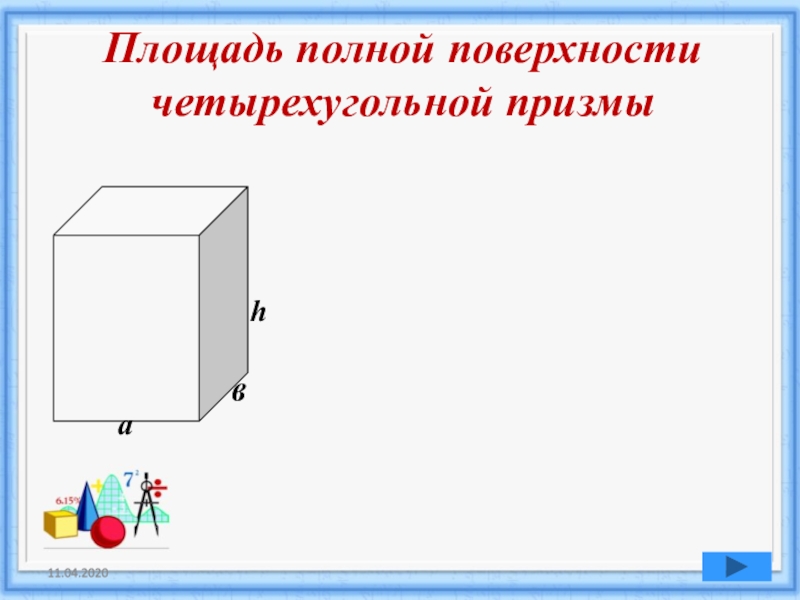
Слайд 14 S =а*в ;где S - площадь
основания, а, в-стороны основания.
S =Р*h; где S -площадь боковой поверхности, h-высота. Р-периметр основания(сумма всех сторон), h-высота призмы. S = S + 2S ;где S -площадь полной поверхности призмы.осн
бок
бок
Площадь полной поверхности четырехугольной призмы
пол
бок
осн
пол
h
в
а
осн
Слайд 15Площадь полной поверхности треугольной призмы
В основаниях находятся треугольники,
площадь треугольника найдем
по теореме Герона: S тр = √ р .( р-а
).(р-в).( р-с); где р –полупериметр треугольника, S =Р*h; где S -площадь боковой поверхности, Р-периметр основания(сумма всех сторон), h-высота призмы. Sпол = Sбок + 2S ; где S -площадь полной поверхности призмы. Площадь полной поверхности правильной призмы
а
в
с
h
осн
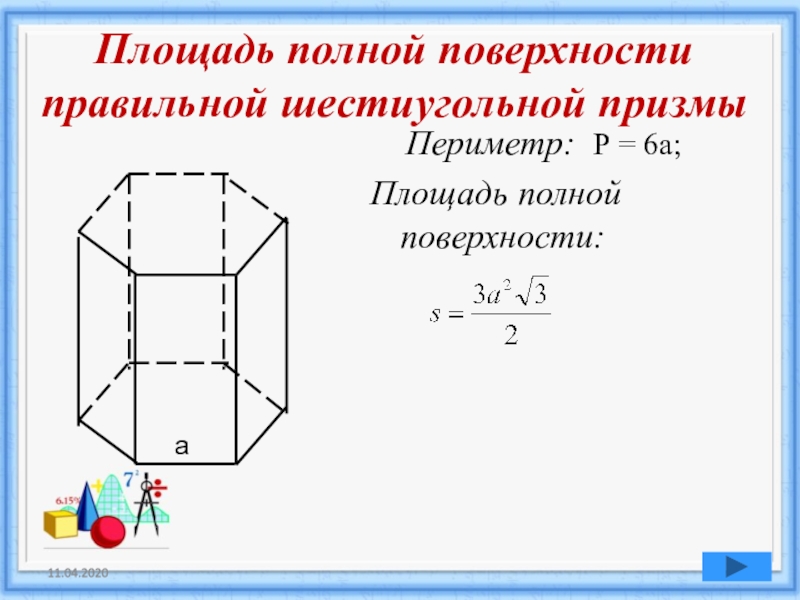
Слайд 16Площадь полной поверхности
правильной шестиугольной призмы
Периметр: Р
= 6а;Площадь полной поверхности:
а
Слайд 17Диагональные сечения призмы
Диагональю призмы называется отрезок, соединяющий
две вершины, не принадлежащие одной грани
Сечения призмы
плоскостями, проходящими через два боковых ребра, не принадлежащих одной грани, называются диагональными сечениямиДиагональные сечения призмы являются параллелограммами
Слайд 18Решение задач
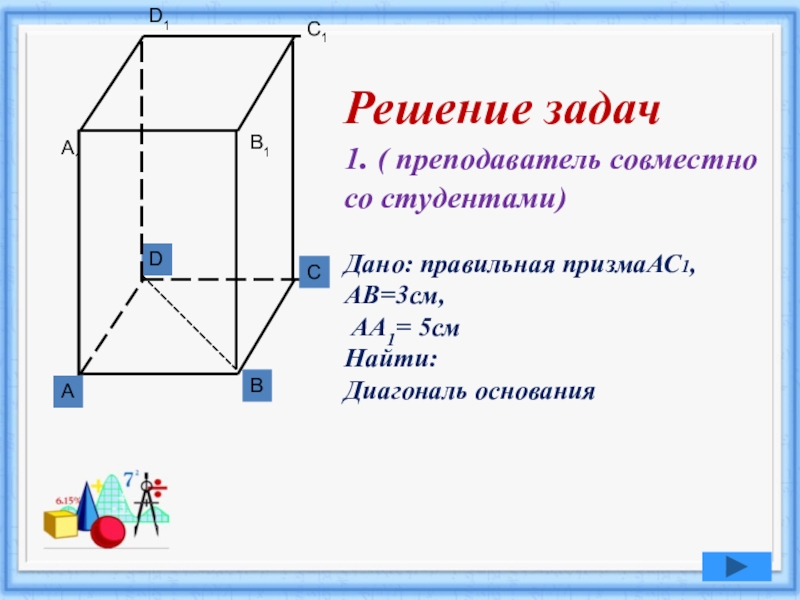
1. ( преподаватель совместно со студентами)
Дано: правильная призмаАС1, АВ=3см,
АА1= 5см
Найти:
Диагональ основания
Слайд 19Решение
Дано: правильная призма, АВ=3см,
АА1= 5см
Найти:
Диагональ основания
Решение: Рассмотрим треугольник АВД.
По теореме Пифагора ВД2= АД2 + АВ2 , следовательно ВД2= 32 + 32 =18; ВД=3√2см
Слайд 21Куб в архитектуре.
В Роттердаме — архитектор наклонил обычный
дом на 45 градусов так, что три грани куба смотрят
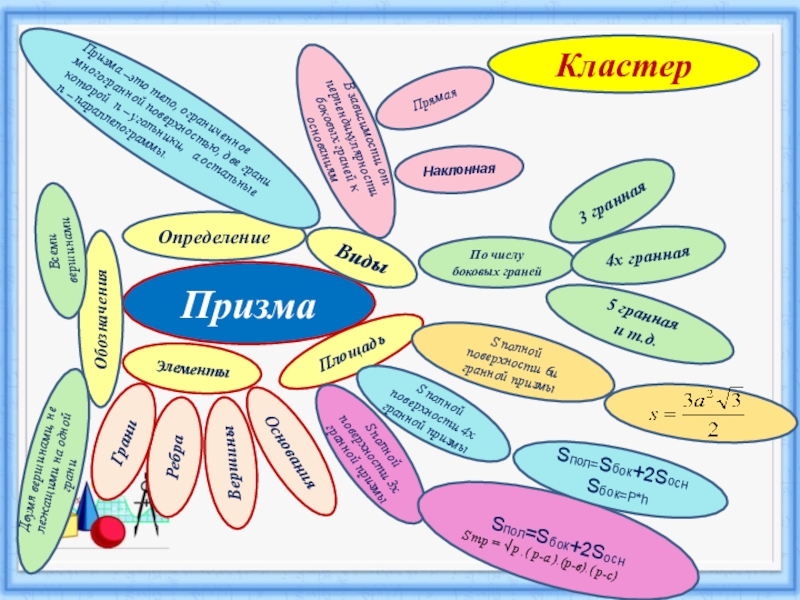
в небо, а три — в землю. Живое воплощение идеи «посмотреть на обычное под другим углом». В каждом из таких кубиков три этажа, что позволяет не чувствовать никаких бытовых неудобств.Слайд 22Призма
Виды
Площадь
Определение
Обозначения
Элементы
В зависимости от перпендикулярности боковых граней к основаниям
S полной поверхности
4х гранной призмы
По числу боковых граней
S полной поверхности 6и гранной
призмыS полной поверхности 3х гранной призмы
Кластер
Основания
Вершины
Ребра
Грани
Всеми вершинами
Двумя вершинами, не лежащими на одной грани
Призма –это тело, ограниченное
многогранной поверхностью, две грани которой n – угольники, а остальные n – параллелограммы.
Sпол=Sбок+2Sосн
Sпол=Sбок+2Sосн Sбок=Р*h
5 гранная и т.д.
4х гранная
3 гранная
Прямая
Наклонная
S тр = √ р .( р-а ).(р-в).( р-с)
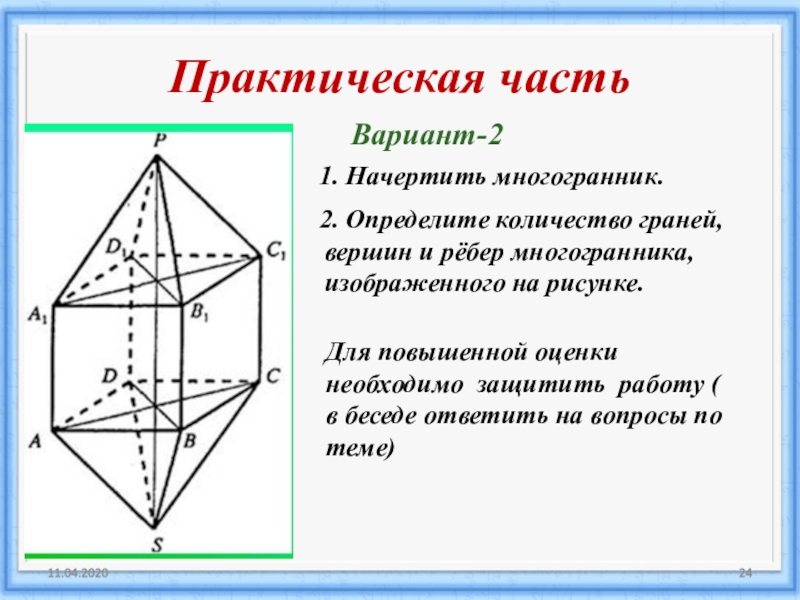
Слайд 23Практическая часть
2.Определите количество граней, вершин и рёбер многогранника, изображенного на
рисунке.
От деревянного кубика отпилили все его вершины.
Вариант-1
1. Начертите куб.
Для повышенной оценки необходимо защитить работу ( в беседе ответить на вопросы по теме)