Прямоугольный параллелепипед и его свойства

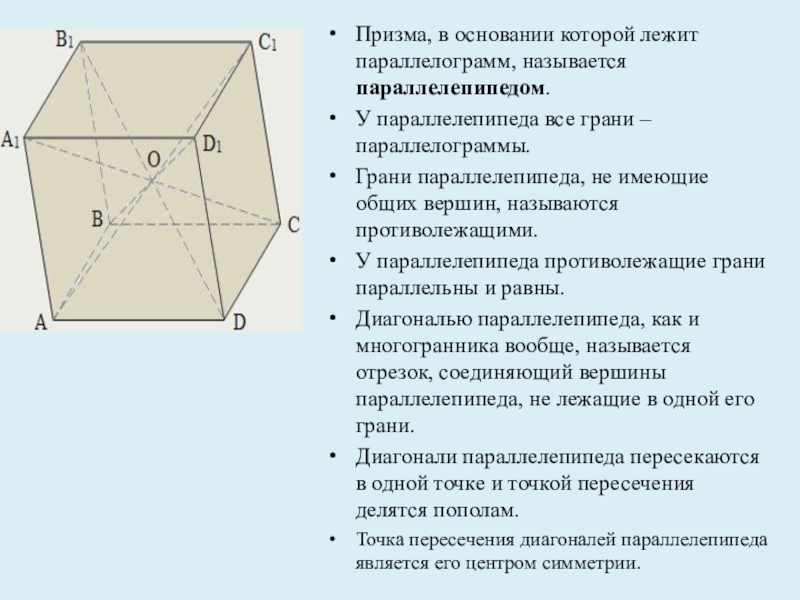
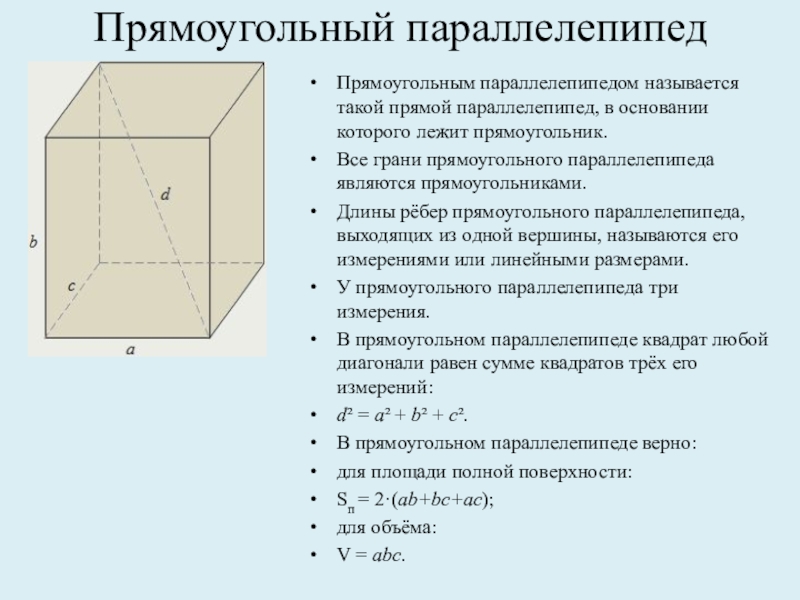
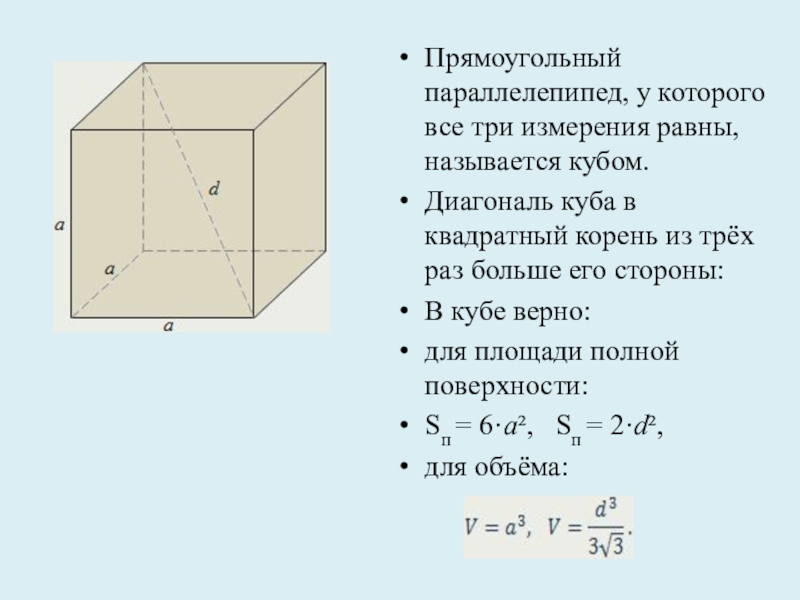
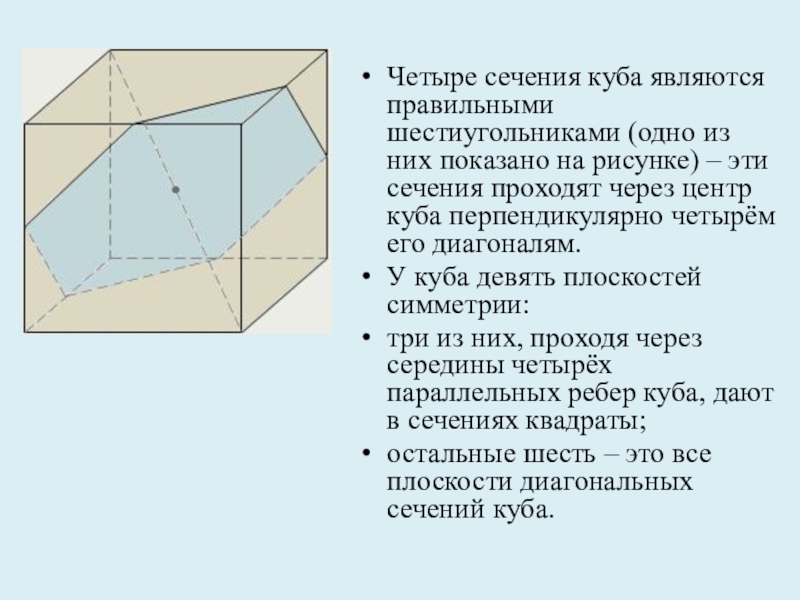
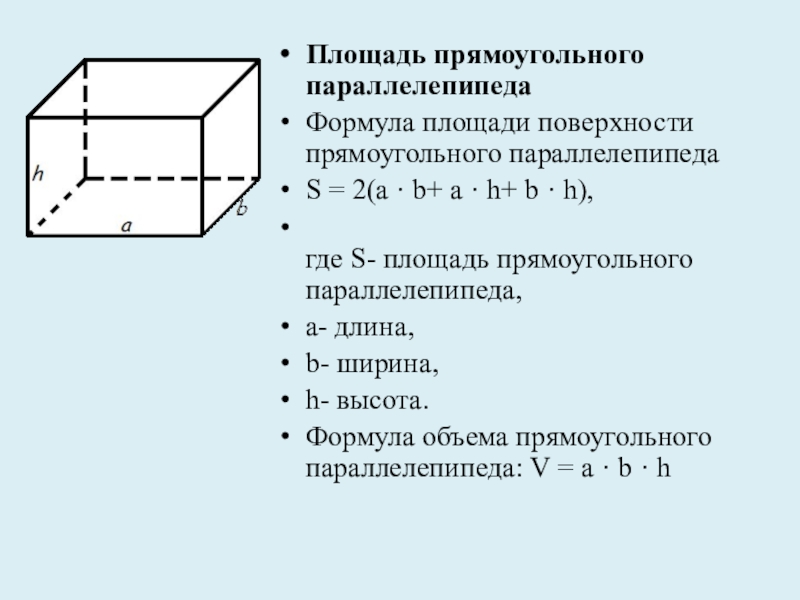
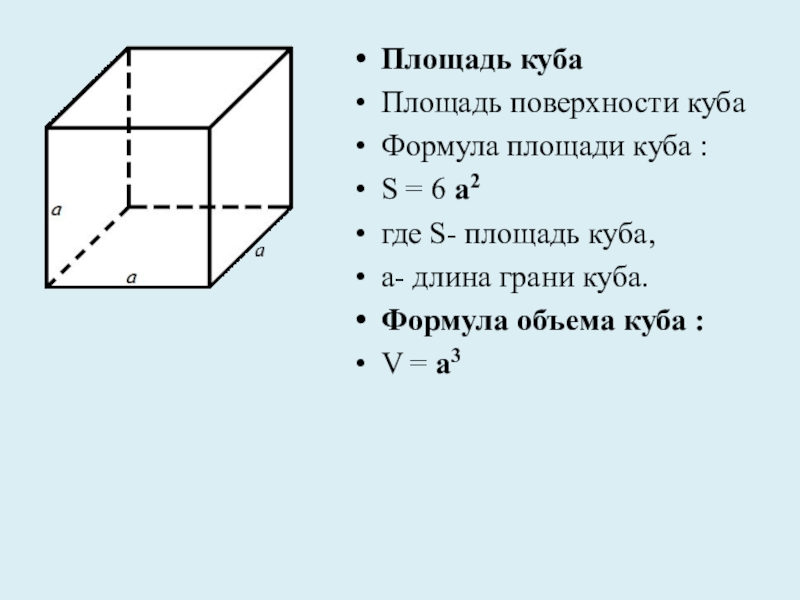
грани – параллелограммы.
Грани параллелепипеда, не имеющие общих вершин, называются противолежащими.
У

параллелепипеда противолежащие грани параллельны и равны.
Диагональю параллелепипеда, как и многогранника вообще, называется отрезок, соединяющий вершины параллелепипеда, не лежащие в одной его грани.
Диагонали параллелепипеда пересекаются в одной точке и точкой пересечения делятся пополам.
Точка пересечения диагоналей параллелепипеда является его центром симметрии.

лежит прямоугольник.
Все грани прямоугольного параллелепипеда являются прямоугольниками.
Длины рёбер прямоугольного параллелепипеда,

выходящих из одной вершины, называются его измерениями или линейными размерами.
У прямоугольного параллелепипеда три измерения.
В прямоугольном параллелепипеде квадрат любой диагонали равен сумме квадратов трёх его измерений:
d² = a² + b² + c².
В прямоугольном параллелепипеде верно:
для площади полной поверхности:
Sп = 2·(ab+bc+ac);
для объёма:
V = abc.

куба в квадратный корень из трёх раз больше его стороны:
В

кубе верно:
для площади полной поверхности:
Sп = 6·a²,   Sп = 2·d²,
для объёма:

на рисунке) – эти сечения проходят через центр куба перпендикулярно

четырём его диагоналям.
У куба девять плоскостей симметрии:
три из них, проходя через середины четырёх параллельных ребер куба, дают в сечениях квадраты;
остальные шесть – это все плоскости диагональных сечений куба.

диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой

пополам.
 Боковые грани прямого параллелепипеда — прямоугольники.
Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
 d 2 = a 2 + b 2 + c2.
Для краткости назовем эту формулу "трёхмерной теоремой Пифагора".

прямоугольного параллелепипеда,
a- длина,
b- ширина,
h- высота.
Формула объема прямоугольного параллелепипеда: V = a

· b · h

площадь куба,
a- длина грани куба.
Формула объема куба :
V = a3

на чертеже упомянутые в условии точки. Соединяем линиями, где это

необходимо. 
3. Ставим известные (заданные) значения прямо на чертеже. 
4. Если получился треугольник внутри тела, то выясняем есть ли в нем прямой угол и какой именно. Для этого пользуемся теоремами о перпендикуляре к плоскости или о трех перпендикулярах.
5. Чертим этот треугольник на плоскости. На нем также отмечаем заданные и искомые величины, если нужно, перенося числа с параллельных ребер.
6. Проводим необходимые вычисления по известным формулам. Как правило, это будут теорема Пифагора и определения синуса и косинуса острых углов прямоугольного треугольника.

Найдите угол  прямоугольного параллелепипеда, для которого

 

Дайте ответ в градусах.