Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Психолого – педагогические основы организации математического развития младших
Содержание
- 1. Психолого – педагогические основы организации математического развития младших
- 2. Математическое развитие Математические способности
- 3. Эльконин Даниил Борисович Давыдов Василий Васильевич Психологическое
- 4. Под математическим развитием ребенка
- 5. Методическая система непрерывного математического развития ребенка способствует:-
- 6. -общему повышению уровня развития интеллектуальных (умственных) способностей
- 7. Цель математического развития ребенка младшего школьного возраста — стимуляция и развитие математического мышления.
- 8. Психолого-дидактическое обоснование: 3—5 лет - наглядно-действенный
- 9. Методологическое обоснование: выбор в качестве ведущего
- 10. Скачать презентанцию
Слайды и текст этой презентации
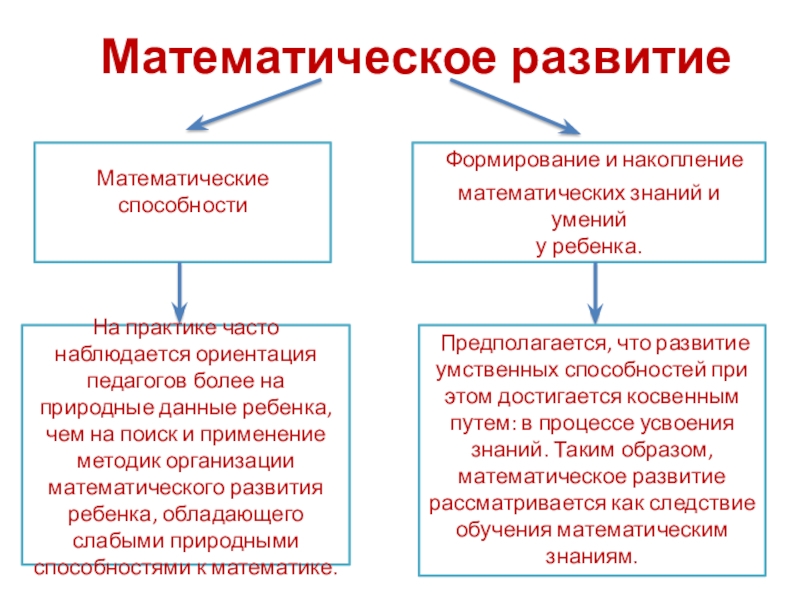
Слайд 2 Математическое развитие
Математические способности
Формирование и накопление
математических знаний и умений у ребенка.
На практике часто наблюдается ориентация педагогов более на природные данные ребенка, чем на поиск и применение методик организации математического развития ребенка, обладающего слабыми природными способностями к математике.
Предполагается, что развитие умственных способностей при этом достигается косвенным путем: в процессе усвоения знаний. Таким образом, математическое развитие рассматривается как следствие обучения математическим знаниям.
Слайд 3Эльконин Даниил Борисович
Давыдов Василий Васильевич
Психологическое обоснование важности и
особой значимости этой проблемы было разработано Д. Б. Элькониным (1960,
1966) и В.В. Давыдовым (1966, 1972), в исследованиях которых было детально показано, что одним из решающих факторов в развитии мышления младших школьников выступает содержание обучения.Доказали, что проблема обновления содержания обучения в начальных классах является частью проблемы организации развивающего обучения ребенка младшего школьного возраста.
Слайд 4 Под математическим развитием ребенка младшего школьного возраста
будем понимать целенаправленное и методически организованное формирование и развитие совокупности
взаимосвязанных основных (базовых) свойств и качеств математического мышления ребенка и его способностей к математическому познанию действительности.Слайд 5Методическая система непрерывного математического развития ребенка способствует:
- практическому созданию единой
системы преемственного дошкольного и начального обучения математике;
- достижению оптимально возможного
для ребенка, соответствующего возрастному этапу уровня математического развития.Слайд 6-общему повышению уровня развития интеллектуальных (умственных) способностей каждого ребенка, что,
в свою очередь, благоприятно отразится на успешности обучения детей;
- личностному
развитию ребенка. Целеустремленность, критичность, широта, гибкость, организованность, логичность и др. являются личностными характеристиками качеств ума и характера человека.
Слайд 7Цель математического развития ребенка младшего школьного возраста —
стимуляция
и развитие
математического мышления.
Слайд 8Психолого-дидактическое обоснование:
3—5 лет - наглядно-действенный тип мышления.
6—10
лет — наглядно-образный тип мышления.
10—12 лет -
переходный к абстрактному (словесно-логическому) типу мышления.Слайд 9Методологическое обоснование: выбор в качестве ведущего метода обучения детей метода
моделирования, с преимущественным использованием на каждом возрастном этапе того вида
моделирования, который более всего соответствует возрастным особенностям развития мышления и других познавательных процессов.В возрасте 3—5 лет — это конструирование (вещественное моделирование);
в возрасте 6—10 лет — сочетание конструирования с графическим моделированием;
в возрасте 10—12 лет — графическое моделирование с элементами конструирования практическое приложение знаний и умений ребенка в математике),