РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 7

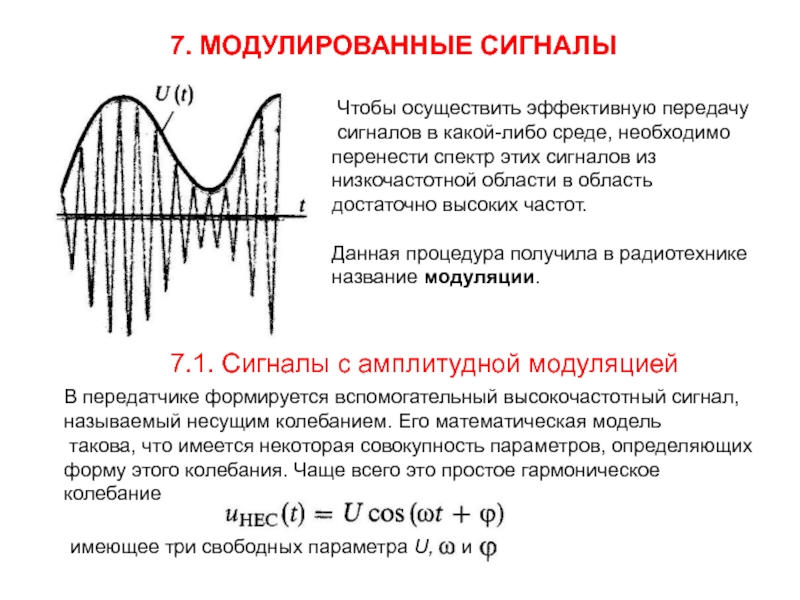
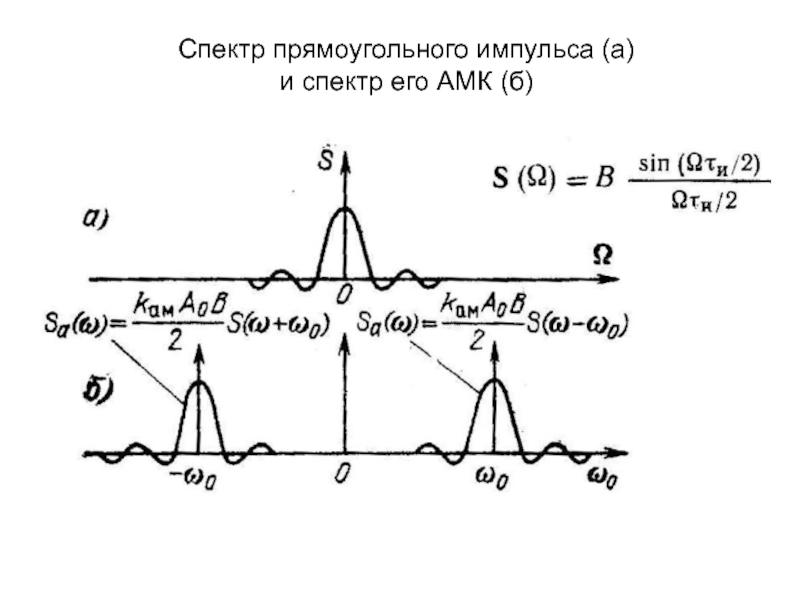
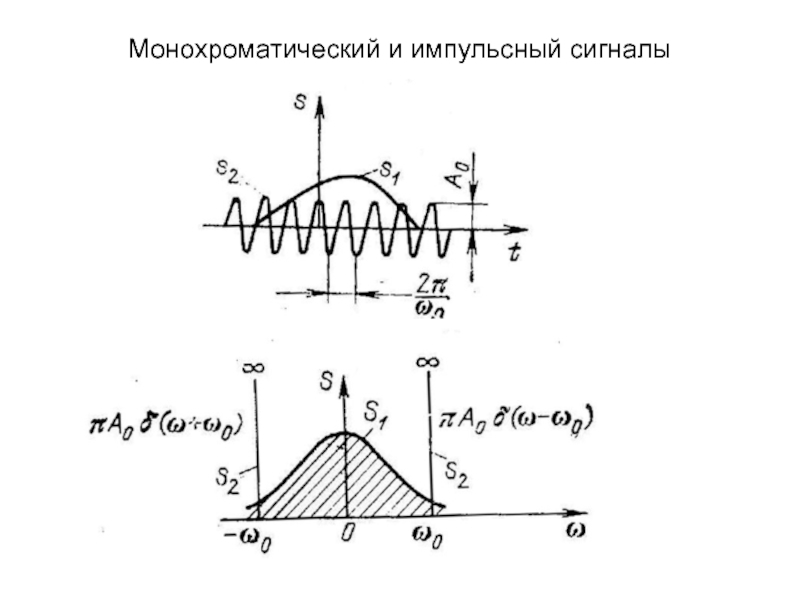
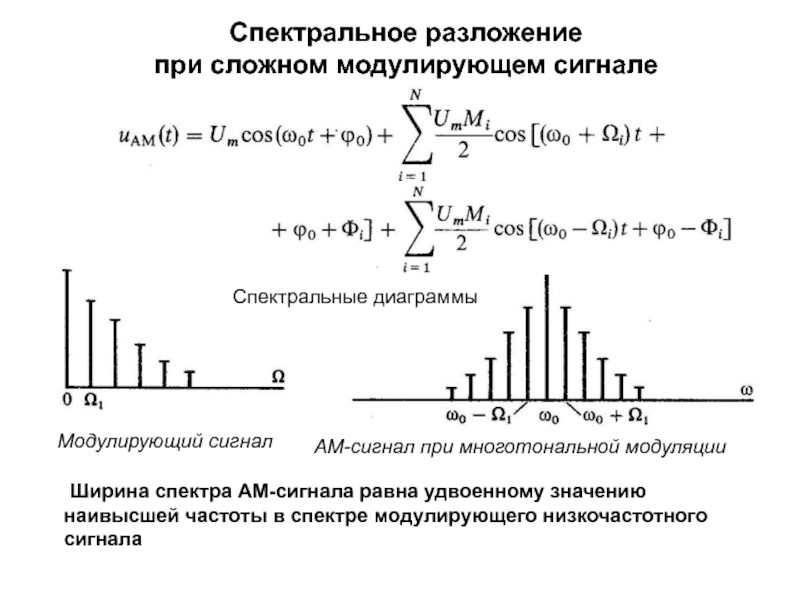
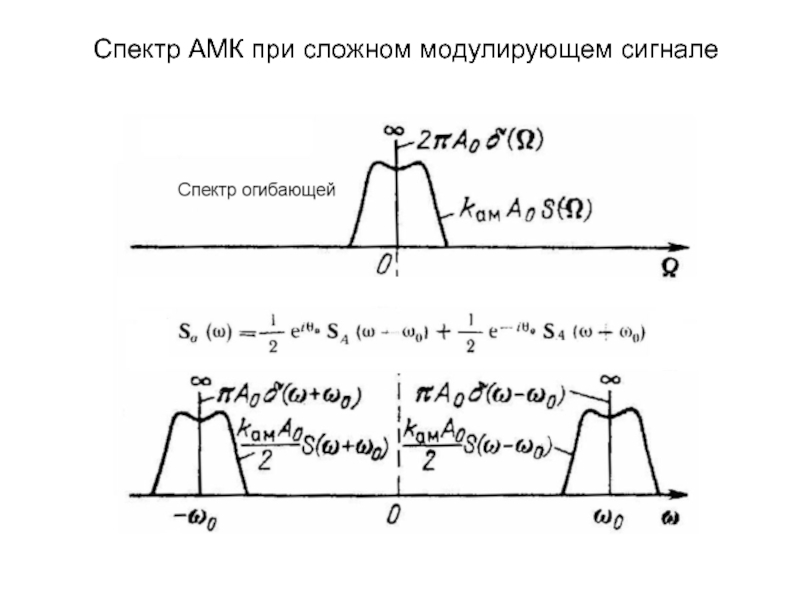
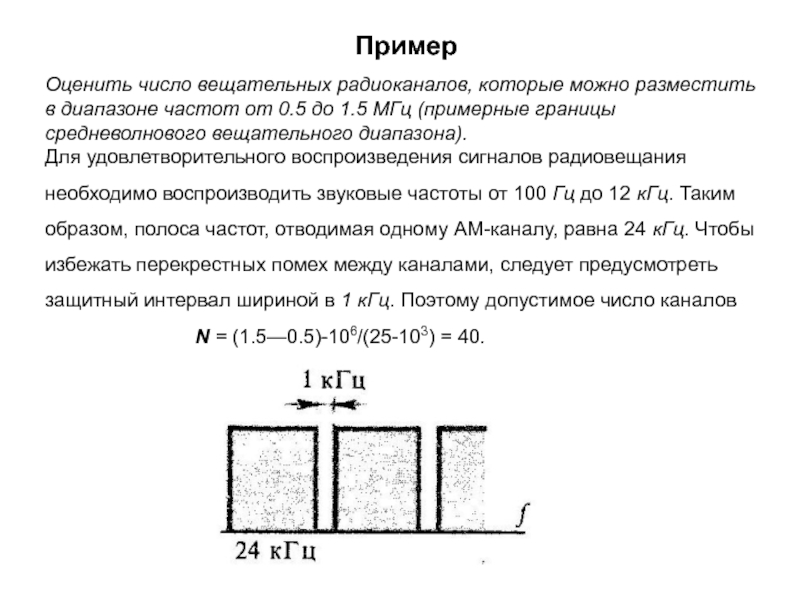
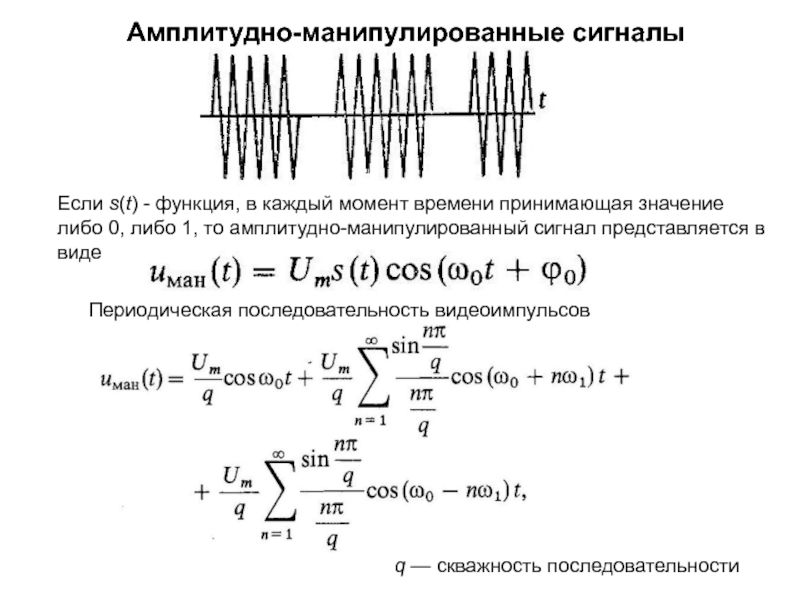
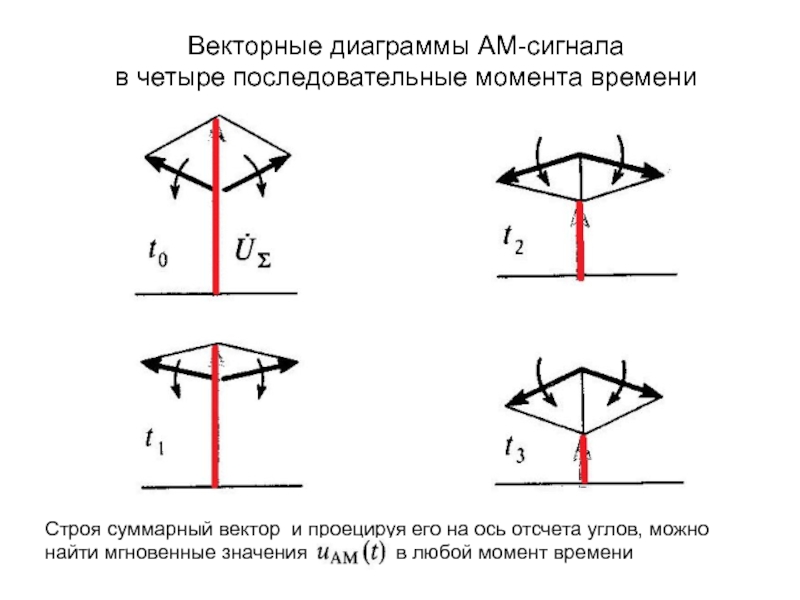
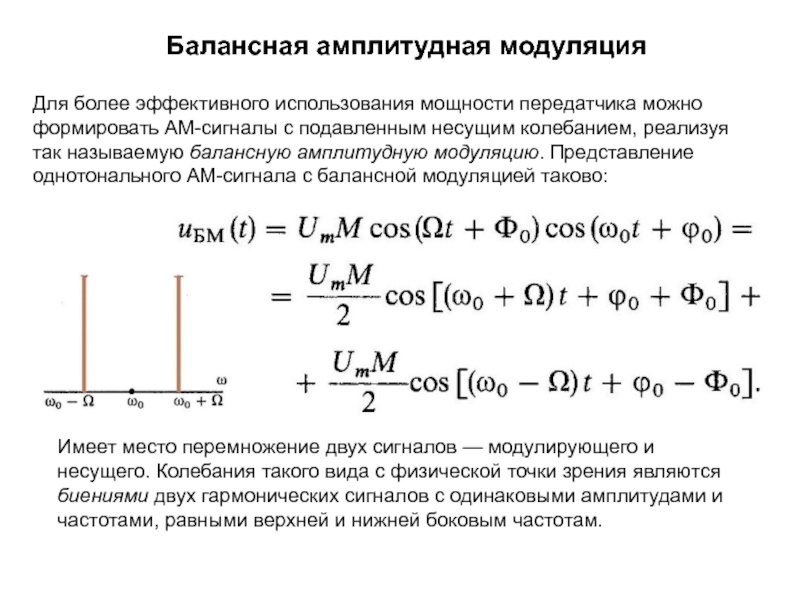
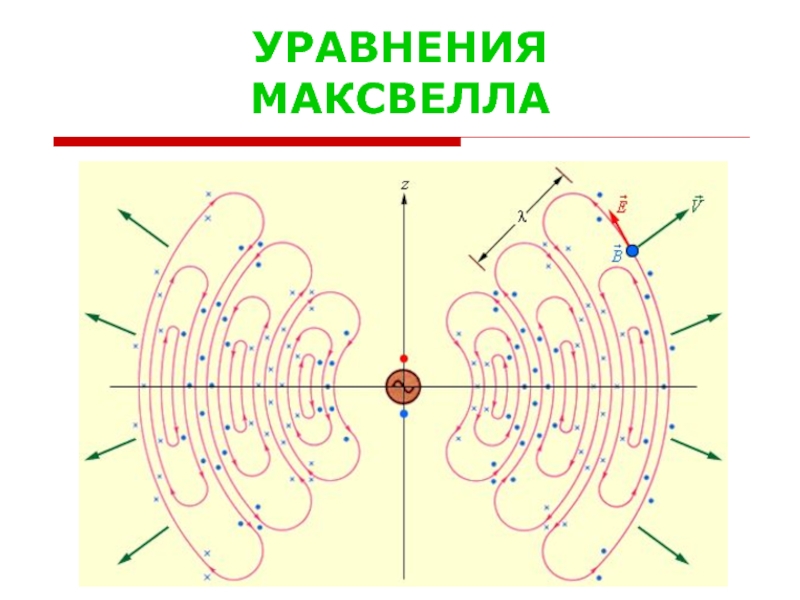
среде, необходимо
перенести спектр этих сигналов из
низкочастотной области в

область
достаточно высоких частот.

Данная процедура получила в радиотехнике
название модуляции.

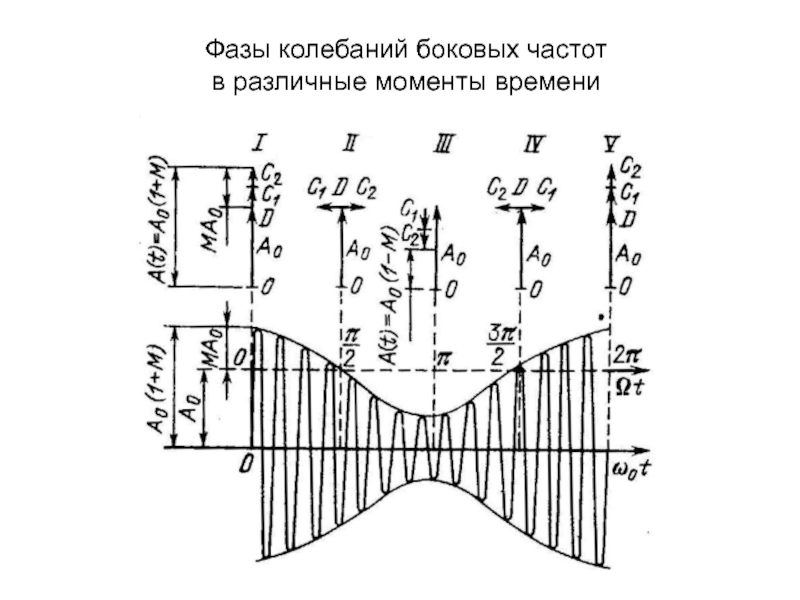
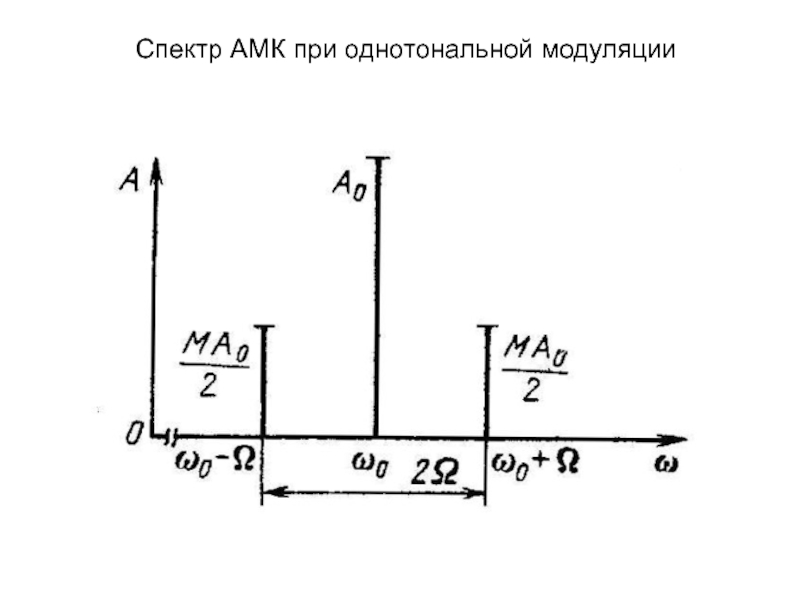
7.1. Сигналы с амплитудной модуляцией

В передатчике формируется вспомогательный высокочастотный сигнал, называемый несущим колебанием. Его математическая модель
такова, что имеется некоторая совокупность параметров, определяющих форму этого колебания. Чаще всего это простое гармоническое колебание

имеющее три свободных параметра U, и

остальные два параметра и и неизменны, то

имеет место амплитудная модуляция несущего колебания.

Пусть s(t) — низкочастотное сообщение, подлежащее передаче по радиоканалу. Если, по крайней мере, один из указанных параметров изменяется во времени пропорционально передаваемому сообщению, то несущее колебание приобретает новое свойство — оно несет в себе информацию, которая первоначально была заключена в сигнале s(t).

Физический процесс управления параметрами несущего колебания и является модуляцией.

АМ-сигнал, его огибающая и несущая

остальные два параметра и и неизменны, то

имеет место амплитудная модуляция несущего колебания.

Пусть s(t) — низкочастотное сообщение, подлежащее передаче по радиоканалу. Если, по крайней мере, один из указанных параметров изменяется во времени пропорционально передаваемому сообщению, то несущее колебание приобретает новое свойство — оно несет в себе информацию, которая первоначально была заключена в сигнале s(t).

Физический процесс управления параметрами несущего колебания и является модуляцией.

АМ-сигнал, его огибающая и несущая

модулирующим полезным сигналом s(t) принято определять следующим образом
Здесь Um —

постоянный коэффициент, равный амплитуде несущего колебания в отсутствие модуляции;
М — коэффициент амплитудной модуляции.

Величина М характеризует глубину амплитудной модуляции.

Иногда вводят дополнительно относительный коэффициент модуляции вверх

и относительный коэффициент модуляции вниз

(|Ms(t)| = 1)
Перемодуляция (|Ms(t)| > 1)

модулирующим низкочастотным сигналом является гармоническое колебание с частотой
Такой сигнал

называется однотональным АМ-сигналом

Спектральный состав однотонального АМ-сигнала

гармонических колебаний
Пусть источники ЭДС нагружены на единичный резистор. Тогда мгновенная

мощность АМ-сигнала будет численно равна квадрату суммарного напряжения

При усреднении все взаимные мощности дадут нулевой результат, поэтому средняя мощность АМ-сигнала окажется равной сумме средних мощностей несущего и боковых колебаний

1) доля мощности обоих боковых колебаний составляет всего лишь 50%

от мощности немодулированного несущего колебания. Поскольку информация о сообщении заключена в боковых колебаниях, можно отметить неэффективность использования мощности при передаче АМ-сигнала.

сложный спектральный состав. Математической моделью такого сигнала может быть, например,

тригонометрическая сумма

Здесь частоты образуют упорядоченную возрастающую последовательность, в то время как амплитуды и начальные фазы произвольны

Введем совокупность парциальных коэффициентов модуляции

модуляции
Ширина спектра АМ-сигнала равна удвоенному значению наивысшей частоты в

спектре модулирующего низкочастотного сигнала

от 0.5 до 1.5 МГц (примерные границы средневолнового вещательного диапазона).
Для

удовлетворительного воспроизведения сигналов радиовещания необходимо воспроизводить звуковые частоты от 100 Гц до 12 кГц. Таким образом, полоса частот, отводимая одному АМ-каналу, равна 24 кГц. Чтобы избежать перекрестных помех между каналами, следует предусмотреть защитный интервал шириной в 1 кГц. Поэтому допустимое число каналов
N = (1.5—0.5)-106/(25-103) = 40.

значение либо 0, либо 1, то амплитудно-манипулированный сигнал представляется в

виде

Периодическая последовательность видеоимпульсов

q — скважность последовательности

комплексной плоскости.
Для простоты рассмотрим однотональную модуляцию. Мгновенное значение несущего

колебания есть проекция неподвижного во времени вектора на ось отсчета углов, которая вращается вокруг начала координат с угловой скоростью в направлении часовой стрелки.

Векторные диаграммы однотонального АМ-сигнала:
а — при t = 0; б — при t > 0

и проецируя его на ось отсчета углов, можно найти мгновенные

значения в любой момент времени

АМ-сигналы с подавленным несущим колебанием, реализуя так называемую балансную амплитудную

модуляцию. Представление однотонального АМ-сигнала с балансной модуляцией таково:

Имеет место перемножение двух сигналов — модулирующего и несущего. Колебания такого вида с физической точки зрения являются биениями двух гармонических сигналов с одинаковыми амплитудами и частотами, равными верхней и нижней боковым частотам.

в том, что при переходе огибающей биений через нуль фаза

высокочастотного заполнения скачком изменяется на 180°, поскольку функция cos(t) имеет разные знаки слева и справа от нуля. Если такой сигнал подать на высокодобротную колебательную систему (например, LC-контур), настроенную на несущую частоту, то выходной эффект будет очень мал, стремясь к нулю при возрастании добротности. Колебания в системе, возбужденные одним периодом биений, будут гаситься последующим периодом. Именно так с физических позиций принято рассматривать вопрос о реальном смысле спектрального разложения сигнала.

от англ. single sideband) по внешним характеристикам напоминают обычные
АМ-сигналы.

Например, однотональный ОБП-сигнал с подавленной нижней боковой частотой записывается в виде

Проводя тригонометрические преобразования, получаем

одна из которых изменяется во времени медленно, а другая —

быстро. Принимая во внимание, что «быстрые» сомножители находятся по отношению друг к другу во временной квадратуре, вычисляем медленно изменяющуюся огибающую ОБП-сигнала

1

— ОБП-сигнала; 2 — обычного АМ-сигнала

частотой
Спектр однополосного сигнала с подавленной несущей частотой
Основное преимущество ОБП-сигналов —

двукратное сокращение полосы занимаемых частот