РАДИОТЕХНИЧЕСКИЕ ЦЕПИ И СИГНАЛЫ 8

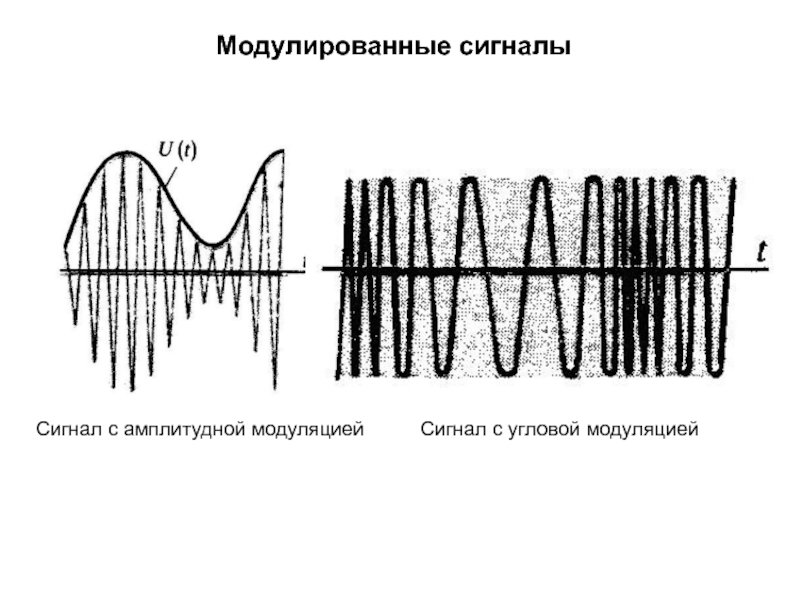
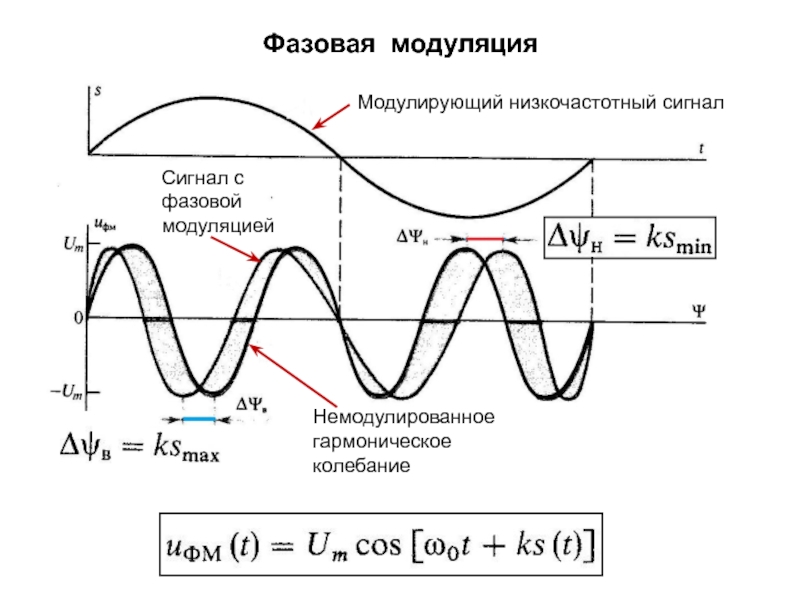
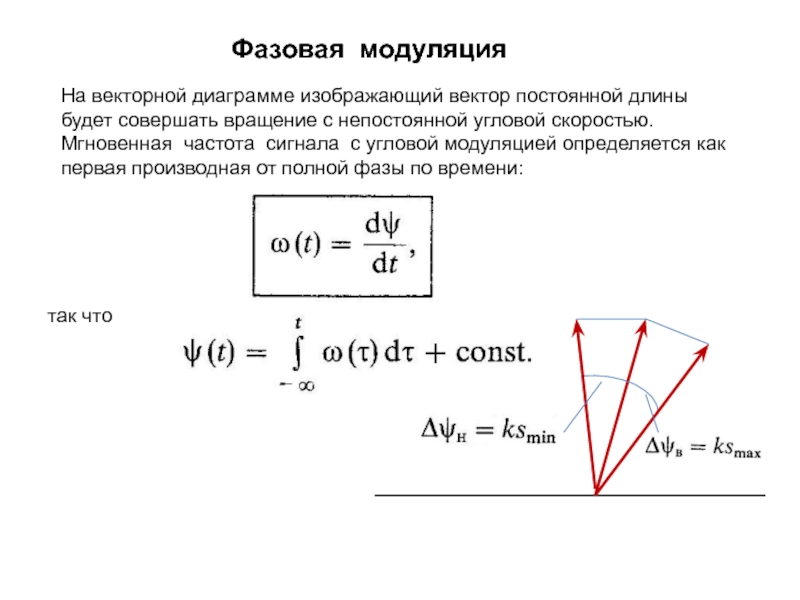
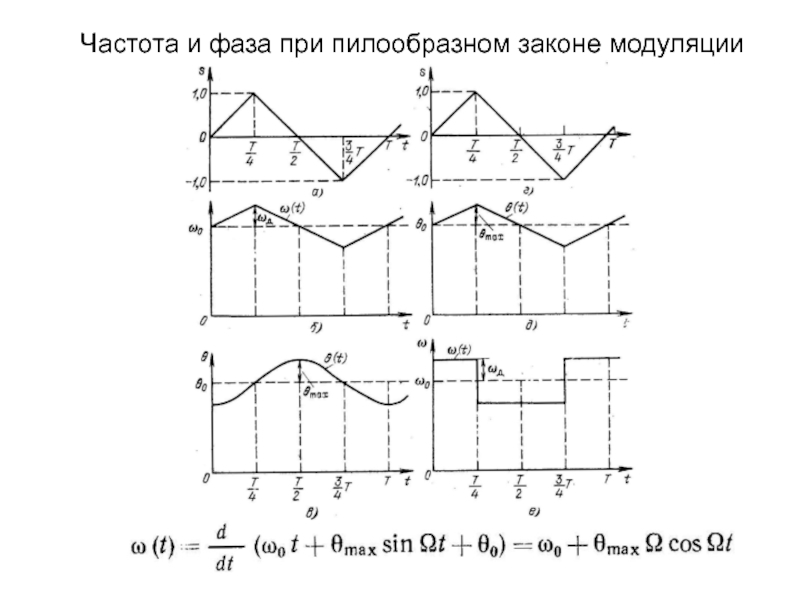
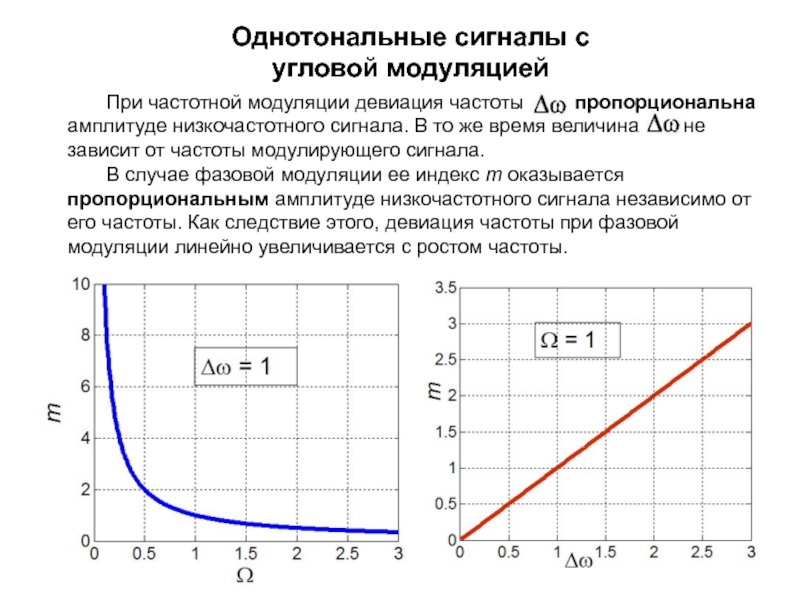
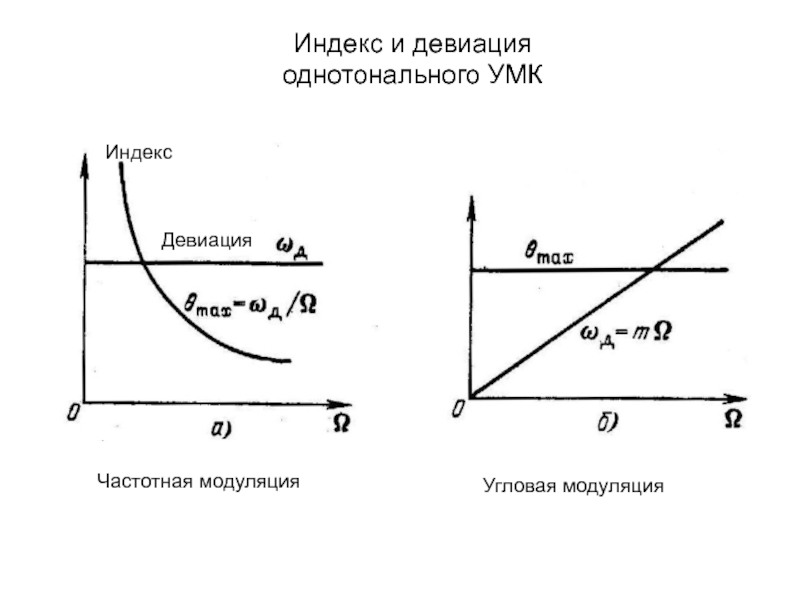
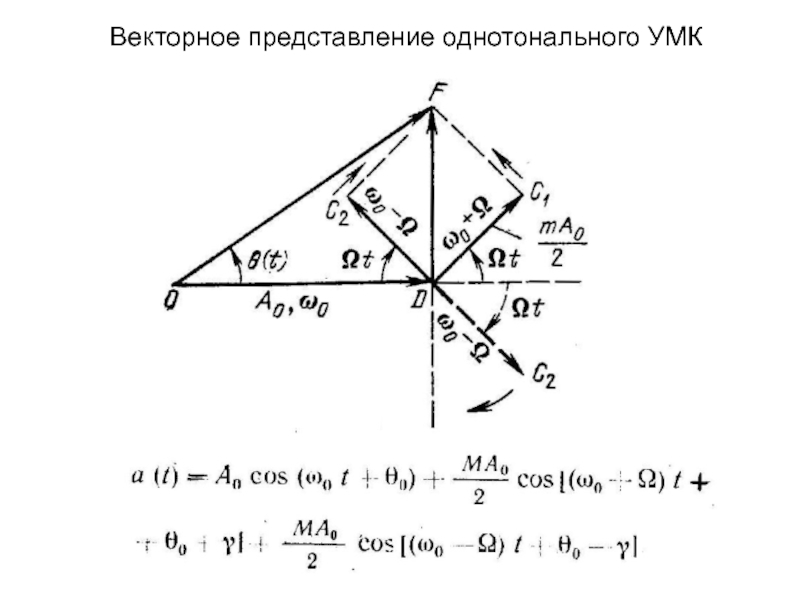
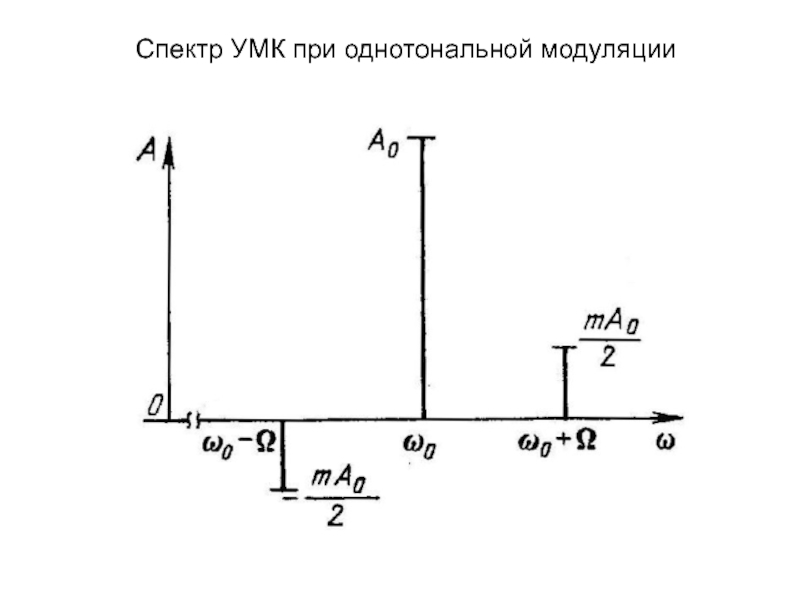
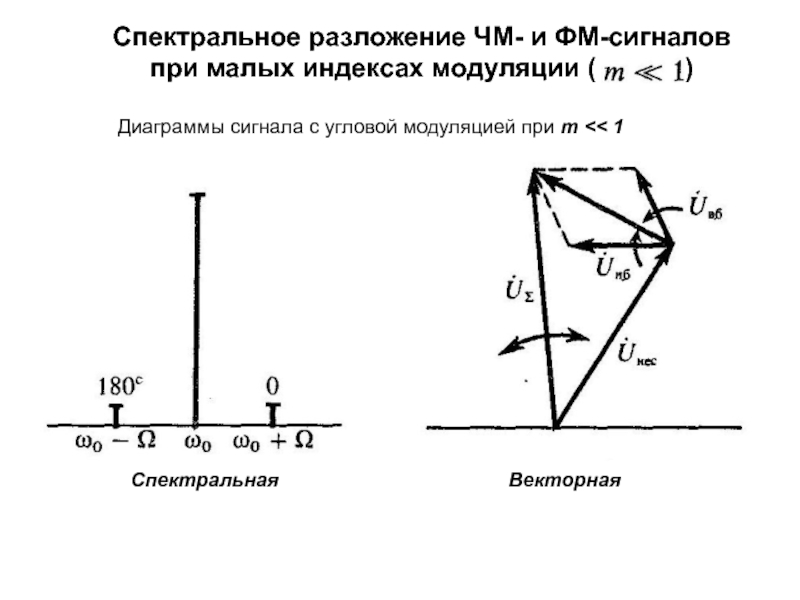
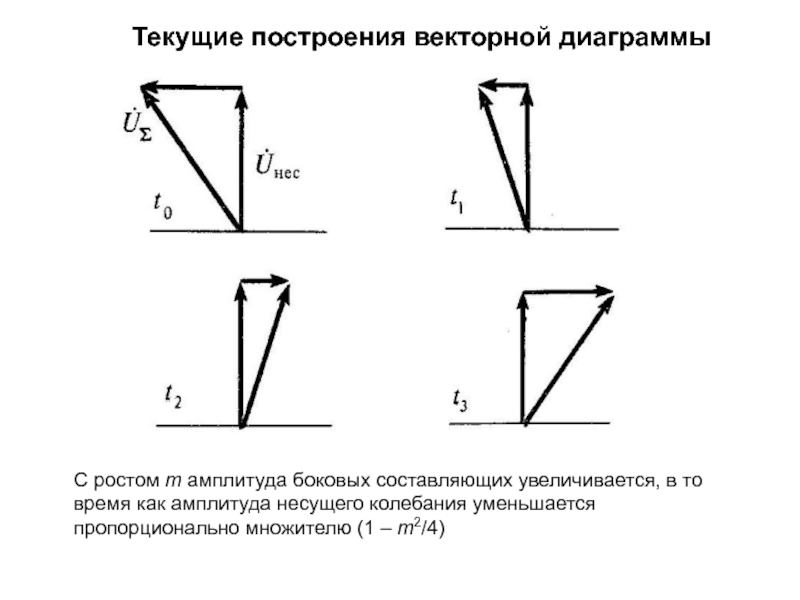
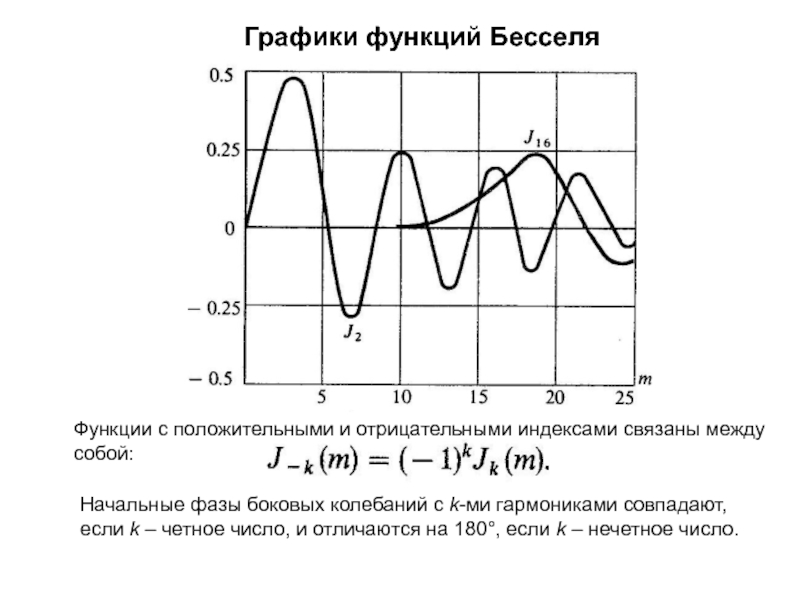
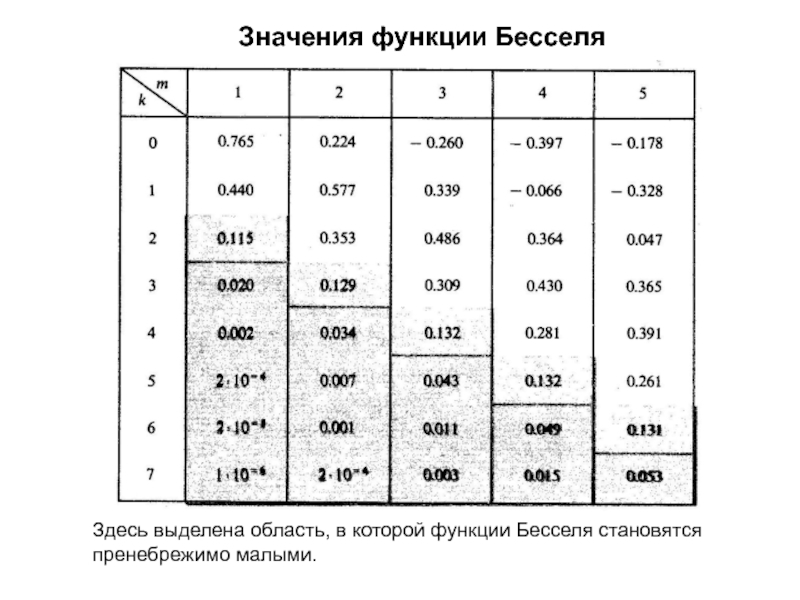
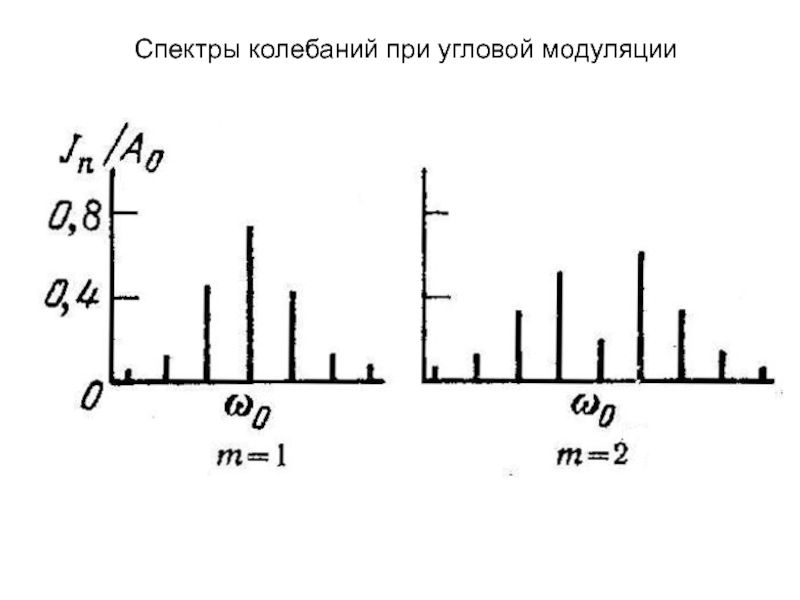
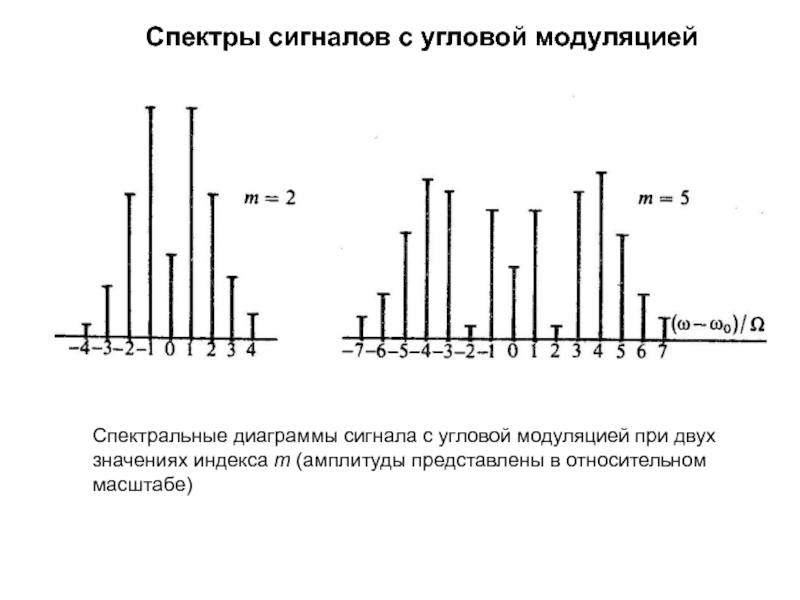
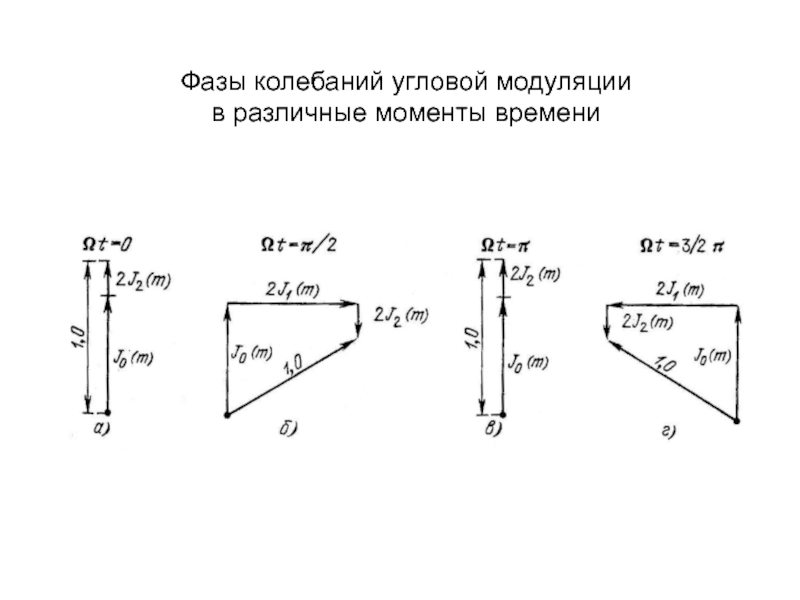
изменяет либо частоту ,
либо начальную фазу

; амплитуда Um остается неизменной.

Поскольку аргумент гармонического колебания , называемый полной фазой, определяет текущее значение фазового угла, такие сигналы получили название
сигналов с угловой модуляцией.

s(t) зависимостью


где — значение частоты в

отсутствие полезного сигнала;
k — некоторый коэффициент пропорциональности. Такую модуляцию называют фазовой модуляцией (ФМ):

Когда сигнал s(t) изменяет знак, принято различать девиацию фазы вверх


и девиацию фазы вниз

будет совершать вращение с непостоянной угловой скоростью. Мгновенная частота сигнала

с угловой модуляцией определяется как первая производная от полной фазы по времени:

величинами s(t) и имеется связь вида


Поэтому
Параметрами ЧМ-сигнала общего вида

в соответствии являются девиация частоты вверх


и девиация частоты вниз

внешне осциллограммы ФМ-
и ЧМ-сигналов не отличаются. Однако имеется принципиальная

разница: фазовый сдвиг между ФМ-сигналом и смодулированным колебанием пропорционален s(t), в то время как для ЧМ-сигнала этот сдвиг пропорционален интегралу от передаваемого сообщения. Например, если
s(t) = Uocos( t), то сигналы с угловой модуляцией будут различаться только количественными параметрами.

математической точки зрения гораздо сложнее, чем исследование АМ-колебаний. Поэтому основное

внимание будет уделено простейшим однотональным сигналам.
В случае однотонального ЧМ-сигнала мгновенная частота

где — девиация частоты сигнала. Полная фаза такого сигнала



где — некоторый постоянный фазовый угол.

Величина



называемая индексом однотональной угловой модуляции, представляет собой девиацию фазы такого сигнала, выраженную в радианах.

частотной модуляции девиация частоты пропорциональна амплитуде

низкочастотного сигнала. В то же время величина не зависит от частоты модулирующего сигнала.
В случае фазовой модуляции ее индекс т оказывается пропорциональным амплитуде низкочастотного сигнала независимо от его частоты. Как следствие этого, девиация частоты при фазовой модуляции линейно увеличивается с ростом частоты.

излучает ФМ-сигнал, промодулированный частотой
F = 15 кГц. Индекс модуляции

m = 12. Найти пределы, в которых изменяется мгновенная частота сигнала.

Математическая модель сигнала имеет вид


Девиация частоты составит
кГц
Таким образом, при модуляции мгновенная частота сигнала изменяется в пределах
от МГц

до МГц

ЧМ-сигнал в виде суммы гармонических колебаний, когда


Для этого преобразуем фазу

= = 0:

Поскольку индекс угловой модуляции мал, воспользуемся приближенными равенствами


поэтому

сигнала с угловой модуляцией

содержатся несущее колебание и две боковые составляющие (верхняя и нижняя) на частотах
и Индекс т играет здесь такую же роль, как коэффициент амплитудной модуляции М.
Однако можно обнаружить и существенное различие спектров АМ-сигнала и колебания с угловой модуляцией. В спектральной диаграмме нижнее боковое колебание имеет дополнительный фазовый сдвиг на 180°.
Сумма векторов, отображающих оба боковых колебания, всегда перпендикулярна вектору несущей. С течением времени вектор
будет «качаться» вокруг центрального положения. Незначительные изменения длины этого вектора обусловлены приближённым характером анализа, и при очень малых т ими можно пренебречь.

)
Векторная
Диаграммы сигнала с угловой модуляцией

при т << 1

Спектральная

сигнала с однотональной угловой модуляцией, помимо известных составляющих, содержатся также

верхние и нижние боковые колебания, соответствующие гармоникам частоты модуляции. Поэтому спектр такого сигнала сложнее спектра аналогичного АМ-сигнала.

Уточним полученный результат, воспользовавшись двумя членами ряда в разложении гармонических функций малого аргумента:

Несложные тригонометрические преобразования приводят к результату:

в то время как амплитуда несущего колебания уменьшается пропорционально множителю

(1 – m2/4)

простейшего случая однотонального ЧМ- или ФМ-сигнала можно найти общее выражение

спектра, справедливое при любом значении индекса модуляции т. Поскольку экспонента с мнимым показателем специального вида, периодическая на отрезке разлагается в комплексный ряд Фурье:

где т — любое вещественное число; — функция Бесселя k-го индекса от аргумента т.

Подставляя перепишем последнюю из указанных формул так:

получаем следующую математическую модель ЧМ-или ФМ-сигнала с любым значением индекса

модуляции:

где т — любое вещественное число; — функция Бесселя k-го индекса от аргумента т.

Спектр однотонального сигнала с угловой модуляцией в общем случае содержит бесконечное число составляющих, частоты которых равны
,

а амплитуды этих составляющих пропорциональны значениям

собой:
Начальные фазы боковых колебаний с k-ми гармониками совпадают, если k

– четное число, и отличаются на 180°, если k – нечетное число.

m
Можно заметить следующее: чем больше индекс функции Бесселя, тем протяженнее

область аргументов, при которых эта функция очень мала.

Важно отметить, что с ростом индекса модуляции расширяется полоса частот, занимаемая сигналом. Обычно полагают, что допустимо пренебречь всеми спектральными составляющими с номерами

Отсюда следует оценка практической ширины спектра сигнала с угловой модуляцией:


Как правило, реальные ЧМ- и ФМ-сигналы характеризуются условием
m > 1. В этом случае

Таким образом, сигнал с угловой модуляцией занимает полосу частот, приблизительно равную удвоенной девиации частоты.

пренебрежимо малыми.

при двух значениях индекса m (амплитуды представлены в относительном масштабе)

мощности в спектре модулированного сигнала. В частности, если значение m

выбрано таким, что Jo(m) = 0, то несущее колебание на частоте
в спектре будет отсутствовать. Значения m, являющиеся корнями данного уравнения, образуют бесконечную возрастающую последовательность чисел mv (v = 1, 2,... — номер корня).

кГц. Найти частоты модуляции F, при которых несущее колебание в

спектре сигнала будет отсутствовать.

Индекс модуляции , т. е. частота модуляции
Обращаясь к таблице, находим последовательность частот, удовлетворяющую поставленному условию:
F1 = 240/2.405 = 99.792 кГц,
F2 = 240/5.520 = 43.474 кГц,
F3 = 240/8.654 = 27.732 кГц
и т. д.

промодулированный по частоте лишь двумя низкими частотами:
Положим, что парциальные индексы

модуляции m1 и m2 малы настолько, что можно пользоваться приближенными выражениями для косинуса и синуса:
Выполнив несколько громоздкие, но вполне элементарные тригонометрические преобразования, представим исходный сигнал

то, что в спектре рассматриваемого сигнала, помимо частот
присутствуют так называемые

комбинационные частоты с четырьмя возможными знаками
.
Амплитуды этих составляющих зависят от произведения парциальных индексов модуляции.

то, что в спектре рассматриваемого сигнала, помимо частот
Спектральная диаграмма сигнала

с двухтональной угловой модуляцией при малых значениях парциальных индексов модуляции m1 и т2.

Амплитуды составляющих диаграммы зависят от произведения парциальных индексов модуляции m1 и т2 .

спектр колебания со сложной угловой модуляцией гораздо богаче спектра аналогичного

АМ-сигнала. Подчеркивая взаимодействие отдельных составляющих модулирующего сигнала, угловую модуляцию, в отличие от амплитудной, иногда называют модуляцией нелинейного типа.

Когда угловая модуляция осуществляется группой низкочастотных колебаний с частотами и парциальными индексами т1, m2 , . . . , mN соответственно, спектральное представление сигнала таково: