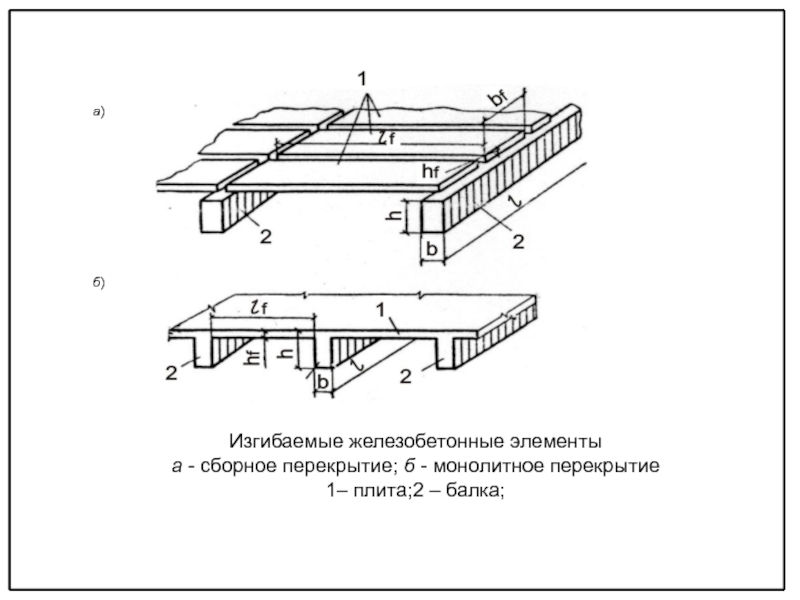
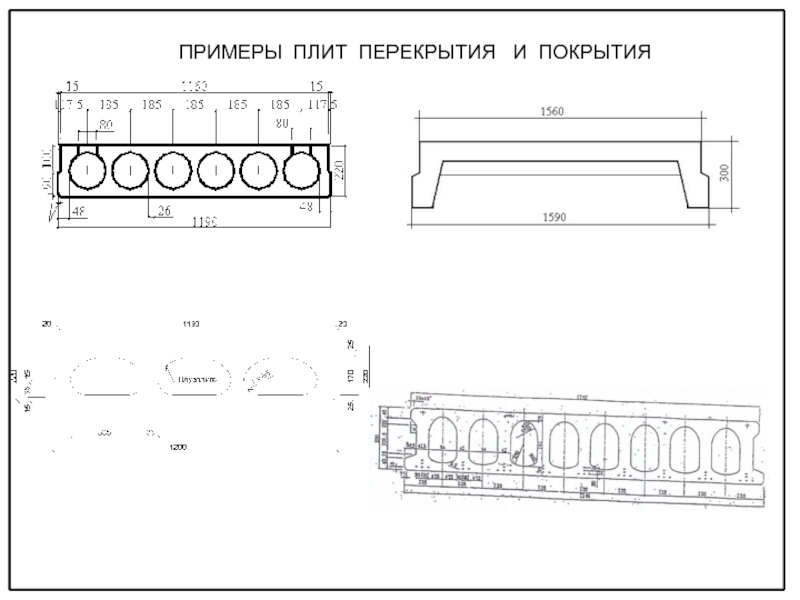
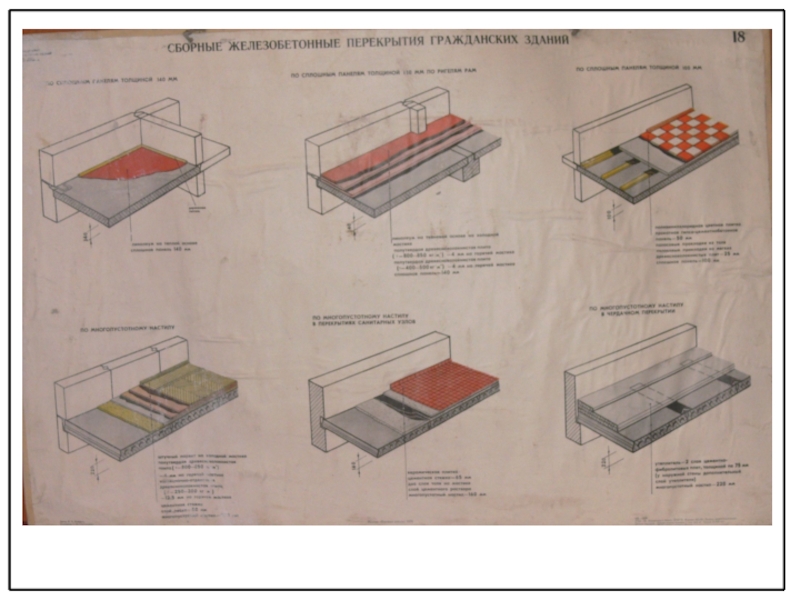
Расчет нормальных сечений

Содержание

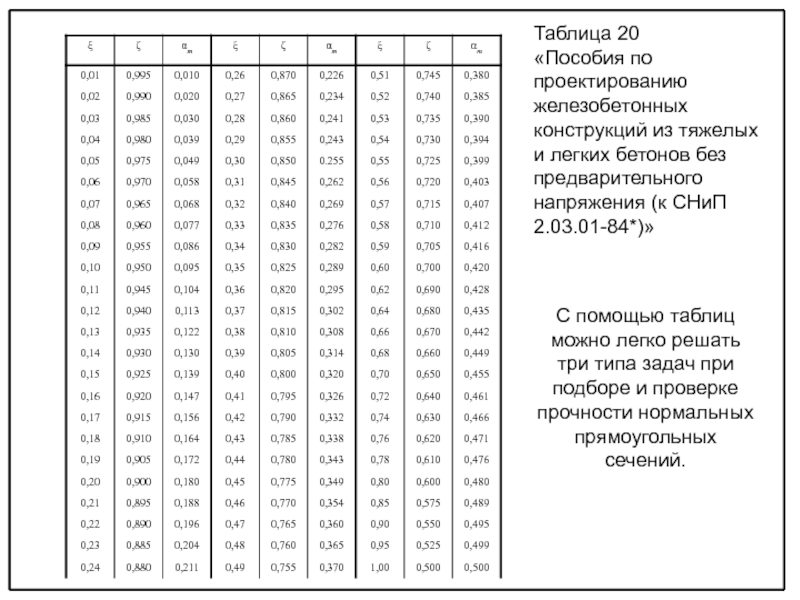
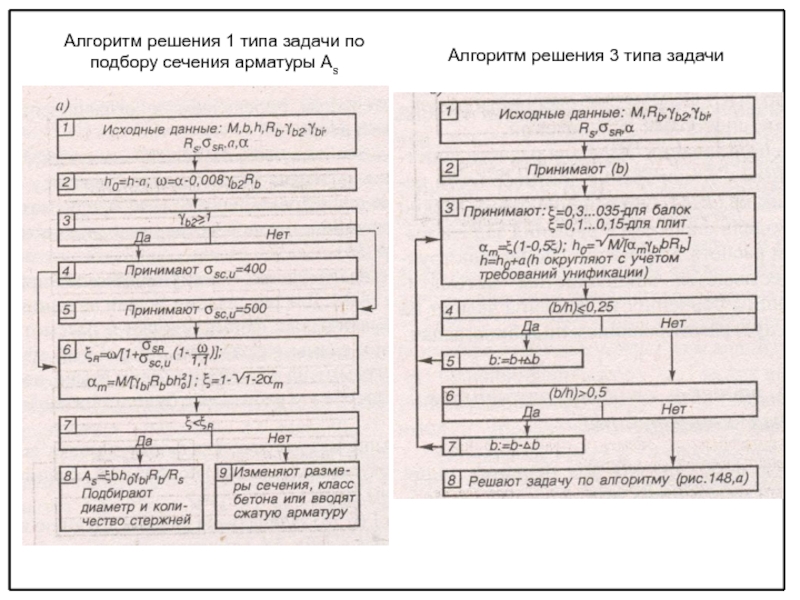
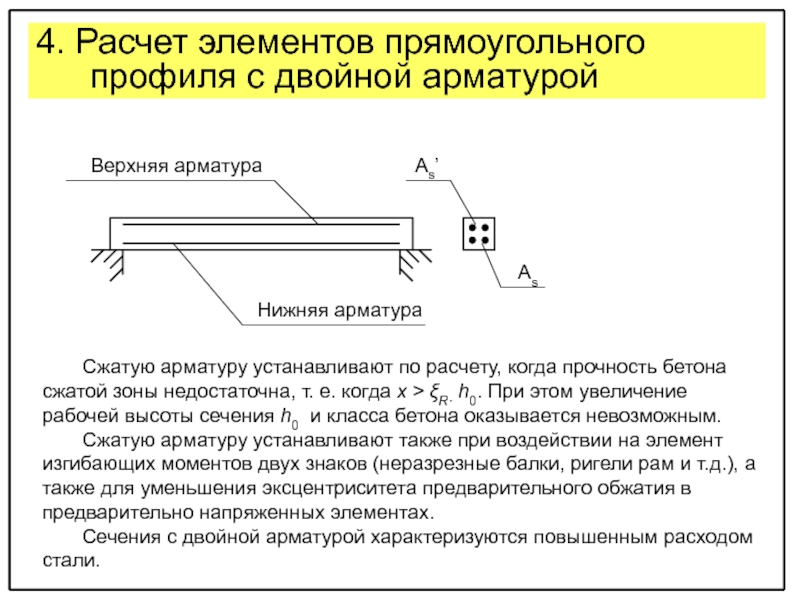
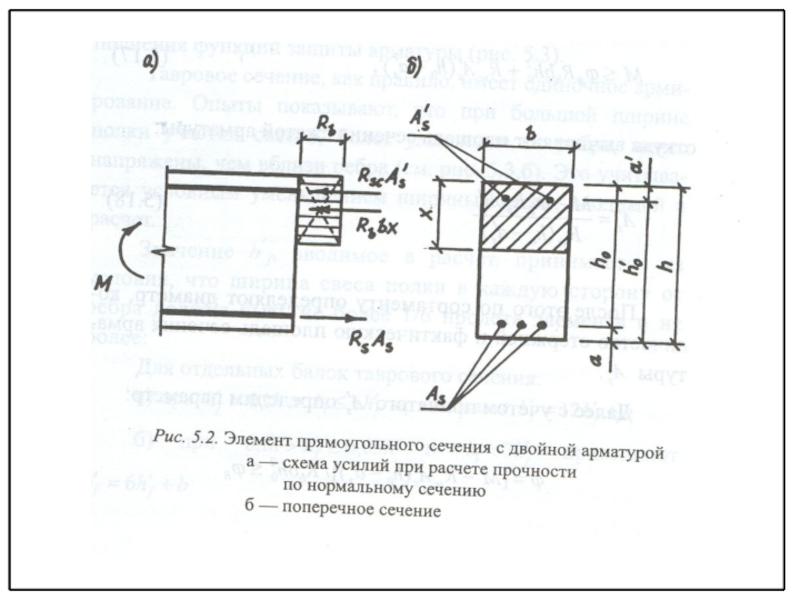
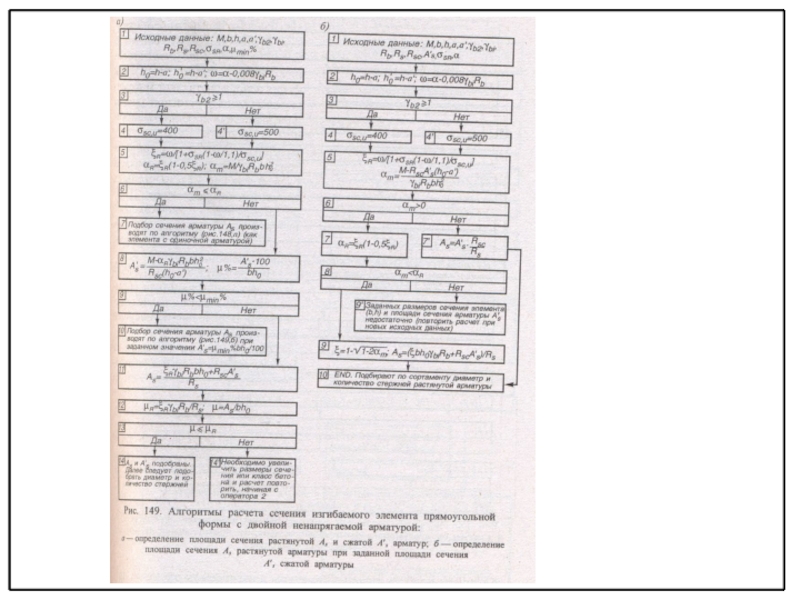
1. Расчет нормальных сечений
2. Вопросы:Общие сведения об изгибаемых железобетонных элементахПредпосылки расчета
3. 1. Общие сведения об изгибаемых железобетонных элементахИзгибаемые элементы Плиты Балки h >h, b
4. Изгибаемые железобетонные элементы а - сборное перекрытие; б - монолитное перекрытие1– плита;2 – балка;
5. ПРИМЕРЫ ПЛИТ ПЕРЕКРЫТИЯ И ПОКРЫТИЯ
6. Слайд 6
7. ПРИМЕРЫ ЖЕЛЕЗОБЕТОННЫХ БАЛОК
8. Слайд 8
9. 2. Предпосылки расчета При расчете приняты следующие
10. Слайд 10
11. Расчетная модель железобетонного изгибаемого элемента прямоугольного профиля
12. Случаи разрушения железобетонного изгибаемого элементаξ > ξR ξ ≤ ξR П. 3.12* СНиП
13. Слайд 13
14. 3. Расчет элементов прямоугольного профиля с одиночной арматуройРасчетная схема qМ=MuЭпюра внутренних усилий dL
15. Схема усилий и напряжений в нормальном расчетном
16. Уравнения равновесияΣNx= 0; RsAs =
17. Преобразуем уравнение (2)Получим илигдеТогда получим где
18. Аналогично преобразуем уравнение (3)тогдагдеВведем илиилиОкончательно получим Или
19. Безразмерные коэффициенты упрощают расчет, зависят от одной
20. Таблица 20 «Пособия по проектированию железобетонных конструкций
21. Проверка несущей способности элемента при заданном армировании,
22. Алгоритм решения 1 типа задачи по подбору сечения арматуры АsАлгоритм решения 3 типа задачи
23. 4. Расчет элементов прямоугольного профиля с двойной
24. Слайд 24
25. М ≤ Мu = Rb b x
26. Слайд 26
27. Скачать презентанцию

Вопросы:Общие сведения об изгибаемых железобетонных элементахПредпосылки расчета Расчет элементов прямоугольного профиля с одиночной арматуройРасчет элементов прямоугольного профиля с двойной арматурой

Главная
Разное
Расчет нормальных сечений

Слайды и текст этой презентации

Слайд 1Томский государственный архитектурно-строительный университет
Кафедра
«Железобетонные и каменные конструкции»
Лекция 8.
Расчет

прочности изгибаемых элементов по нормальным сечениям
Тема 3.

Расчет железобетонных изгибаемых элементов по прочности

Дисциплина
«ЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ»
Часть I
Курс лекций

Составитель: В. В. Родевич

Томский государственный архитектурно-строительный университет Кафедра «Железобетонные и каменные конструкции»Лекция 8.Расчет прочности изгибаемых элементов по нормальным сечениям

Слайд 2Вопросы:
Общие сведения об изгибаемых железобетонных элементах

Предпосылки расчета

Расчет элементов прямоугольного

профиля с одиночной арматурой

Расчет элементов прямоугольного профиля с двойной арматурой

Вопросы:Общие сведения об изгибаемых железобетонных элементахПредпосылки расчета Расчет элементов прямоугольного профиля с одиночной арматуройРасчет элементов прямоугольного профиля

Слайд 31. Общие сведения об изгибаемых железобетонных элементах
Изгибаемые элементы
Плиты
Балки

h >h, b

1. Общие сведения об изгибаемых железобетонных элементахИзгибаемые элементы Плиты Балки h >h, b

Слайд 4Изгибаемые железобетонные элементы
а - сборное перекрытие; б - монолитное

перекрытие
1– плита;2 – балка;

Слайд 5ПРИМЕРЫ ПЛИТ ПЕРЕКРЫТИЯ И ПОКРЫТИЯ

Слайд 6

Слайд 7ПРИМЕРЫ ЖЕЛЕЗОБЕТОННЫХ БАЛОК

Слайд 8

Слайд 92. Предпосылки расчета
При расчете приняты следующие предпосылки:
Разрушение железобетонного

изгибаемого элемента
1- по нормальному сечению; 2- по наклонному сечению

2. Предпосылки расчета При расчете приняты следующие предпосылки: Разрушение железобетонного изгибаемого элемента 1- по нормальному сечению; 2-

Слайд 10

Слайд 11Расчетная модель железобетонного изгибаемого элемента
прямоугольного профиля

Слайд 12Случаи разрушения железобетонного изгибаемого элемента
ξ > ξR
ξ ≤ ξR

П. 3.12* СНиП

Слайд 13

Слайд 143. Расчет элементов прямоугольного профиля с одиночной арматурой
Расчетная схема
q

М=Mu
Эпюра

внутренних усилий

dL

Слайд 15Схема усилий и напряжений в нормальном расчетном сечении элемента прямоугольной

формы с одиночной арматурой
Ab = bx; zb =

h0 – 0,5х;

Схема усилий и напряжений в нормальном расчетном сечении элемента прямоугольной формы с одиночной арматурой Ab =

Слайд 16Уравнения равновесия

ΣNx= 0;
RsAs = Rb·bx; (1)

∑MS =0;
M ≤

Rb ·bx(h0 - 0.5x); (2)

∑Mb = 0
M ≤ RsAs(h0 - 0.5x); (3)
Из

уравнения (1) получим: X=Rs·As/(Rb·b)

Уравнения равновесияΣNx= 0; RsAs = Rb·bx; (1)∑MS =0; M ≤ Rb ·bx(h0 - 0.5x); (2)∑Mb = 0 M ≤

Слайд 17Преобразуем уравнение (2)

Получим
или
где

Тогда получим
где

Слайд 18Аналогично преобразуем уравнение (3)

тогда
где
Введем
или
или
Окончательно получим
Или

Слайд 19Безразмерные коэффициенты упрощают расчет, зависят от одной величины и позволяют

свести данные в таблицу.

Такой метод расчета называют
табличным методом

расчета железобетонных изгибаемых элементов по нормальным сечениям

Безразмерные коэффициенты упрощают расчет, зависят от одной величины и позволяют свести данные в таблицу. Такой метод расчета

Слайд 20

Таблица 20
«Пособия по проектированию железобетонных конструкций из тяжелых и

легких бетонов без предварительного напряжения (к СНиП 2.03.01-84*)»
С помощью таблиц

можно легко решать три типа задач при подборе и проверке прочности нормальных прямоугольных сечений.

Таблица 20 «Пособия по проектированию железобетонных конструкций из тяжелых и легких бетонов без предварительного напряжения (к СНиП

Слайд 21

Проверка несущей способности элемента при заданном армировании, известных размерах сечения,

видах и классах бетона и арматуры, класса ответственности здания по

назначению.

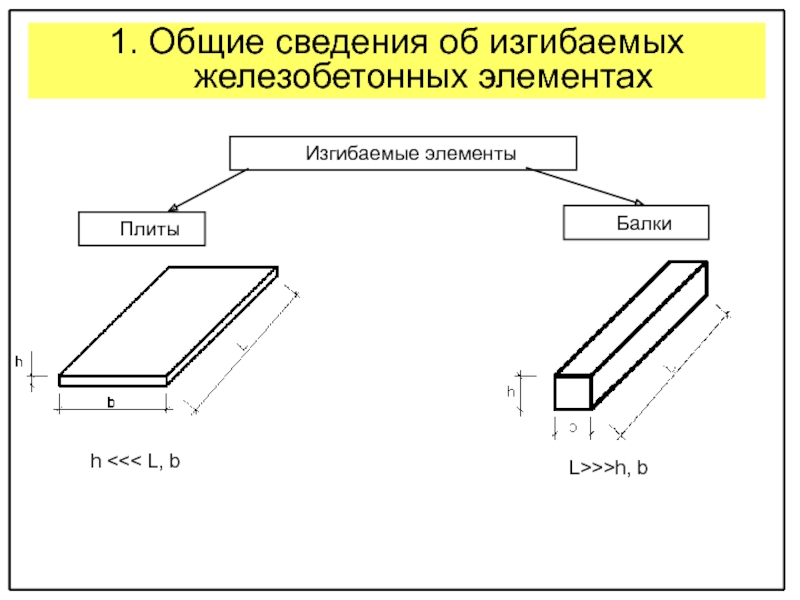
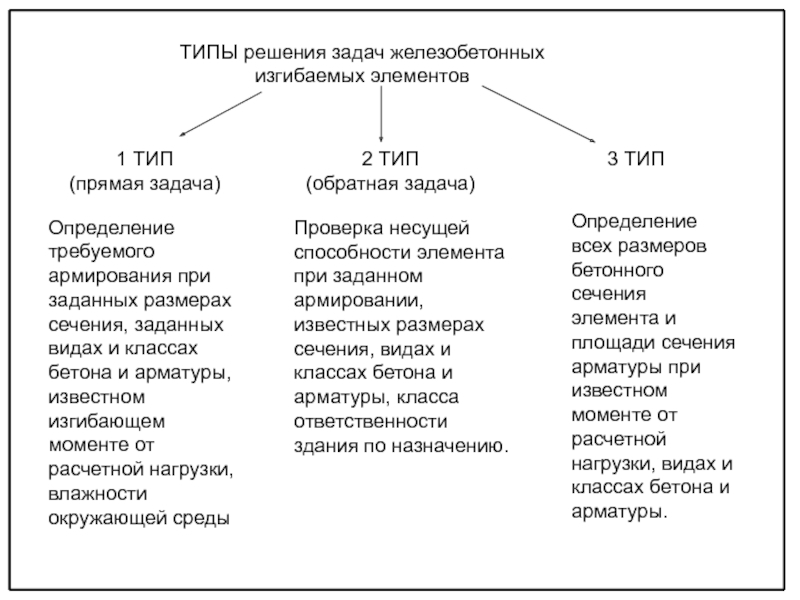
ТИПЫ решения задач железобетонных изгибаемых элементов

1 ТИП
(прямая задача)

2 ТИП
(обратная задача)

3 ТИП

Определение требуемого армирования при заданных размерах сечения, заданных видах и классах бетона и арматуры, известном изгибающем моменте от расчетной нагрузки, влажности окружающей среды

Определение всех размеров бетонного сечения элемента и площади сечения арматуры при известном моменте от расчетной нагрузки, видах и классах бетона и арматуры.

Проверка несущей способности элемента при заданном армировании, известных размерах сечения, видах и классах бетона и арматуры, класса

Слайд 22

Алгоритм решения 1 типа задачи по подбору сечения арматуры Аs
Алгоритм

решения 3 типа задачи

Слайд 234. Расчет элементов прямоугольного профиля с двойной арматурой

Нижняя арматура
Верхняя

арматура

Аs
Аs’
Сжатую арматуру устанавливают по расчету, когда прочность бетона

сжатой зоны недостаточна, т. е. когда х > ξR· h0. При этом увеличение рабочей высоты сечения h0 и класса бетона оказывается невозможным.
Сжатую арматуру устанавливают также при воздействии на элемент изгибающих моментов двух знаков (неразрезные балки, ригели рам и т.д.), а также для уменьшения эксцентриситета предварительного обжатия в предварительно напряженных элементах.
Сечения с двойной арматурой характеризуются повышенным расходом стали.

4. Расчет элементов прямоугольного профиля с двойной арматуройНижняя арматура Верхняя арматура Аs Аs’ Сжатую арматуру устанавливают по расчету,

Слайд 24

Слайд 25М ≤ Мu = Rb b x (h0 – 0.5x)

+ Rsc As′ (h0 – a′),
Условие прочности
Rb b

x + Rsc As′ - Rs As = 0,

откуда

М ≤ Мu = Rb b x (h0 – 0.5x) + Rsc As′ (h0 – a′), Условие

Слайд 26

Скачать презентацию

Разделы презентаций

Расчет нормальных сечений

Содержание

Слайды и текст этой презентации

Слайд 1Томский государственный архитектурно-строительный университет Кафедра «Железобетонные и каменные конструкции»Лекция 8.Расчет

прочности изгибаемых элементов по нормальным сечениям Тема 3.

Слайд 2Вопросы:Общие сведения об изгибаемых железобетонных элементахПредпосылки расчета Расчет элементов прямоугольного

профиля с одиночной арматуройРасчет элементов прямоугольного профиля с двойной арматурой

Слайд 31. Общие сведения об изгибаемых железобетонных элементахИзгибаемые элементы Плиты Балки

h >h, b

Слайд 4Изгибаемые железобетонные элементы а - сборное перекрытие; б - монолитное

перекрытие1– плита;2 – балка;

Слайд 5ПРИМЕРЫ ПЛИТ ПЕРЕКРЫТИЯ И ПОКРЫТИЯ

Слайд 6

Слайд 7ПРИМЕРЫ ЖЕЛЕЗОБЕТОННЫХ БАЛОК

Слайд 8

Слайд 92. Предпосылки расчета При расчете приняты следующие предпосылки: Разрушение железобетонного

изгибаемого элемента 1- по нормальному сечению; 2- по наклонному сечению

Слайд 10

Слайд 11Расчетная модель железобетонного изгибаемого элемента прямоугольного профиля

Слайд 12Случаи разрушения железобетонного изгибаемого элементаξ > ξR ξ ≤ ξR

П. 3.12* СНиП

Слайд 13

Слайд 143. Расчет элементов прямоугольного профиля с одиночной арматуройРасчетная схема qМ=MuЭпюра

внутренних усилий dL

Слайд 15Схема усилий и напряжений в нормальном расчетном сечении элемента прямоугольной

формы с одиночной арматурой Ab = bx; zb =

Слайд 16Уравнения равновесияΣNx= 0; RsAs = Rb·bx; (1)∑MS =0; M ≤

Rb ·bx(h0 - 0.5x); (2)∑Mb = 0 M ≤ RsAs(h0 - 0.5x); (3)Из

Слайд 17Преобразуем уравнение (2)Получим илигдеТогда получим где

Слайд 18Аналогично преобразуем уравнение (3)тогдагдеВведем илиилиОкончательно получим Или