Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Распараллеливание некоторых численных методов
Содержание
- 1. Распараллеливание некоторых численных методов
- 2. ПланНахождение суммы значенийУмножение матрицРешение систем линейных уравнений
- 3. Сумма последовательности значенийНахождение суммы большого количества слагаемыхЧисленное
- 4. Походы к распараллеливанию суммированияКонвейеризация последовательности операцийВекторизацияРазбиение цикла на блоки
- 5. Разбиение цикла на блокиСуммирование ассоциативноЦикл разбивается на
- 6. Оценка количества операцийВремя выполнения последовательного алгоритмаNf –
- 7. Эффективность распараллеливания суммированияКоэффициент эффективностиУскорение при распараллеливании будет
- 8. Конвейер Количество пересылок равно p-1Эффективность ниже, чем
- 9. Графическая иллюстрацияКонвейер дает худшие результаты по ускорению,
- 10. Умножение матрицБлочное представление дает возможность вычислять блок
- 11. Алгоритм ФоксаКаждый процессор pij вычисляет свой блок
- 12. Алгоритм Фокса (продолжение)На каждой итерации алгоритма, номер
- 13. Оценка времени Алгоритма ФоксаВремя одной итерации равно
- 14. ХарактеристикиАлгоритм содержит как конвейерные так и параллельные
- 15. Решение систем линейных уравненийЕсть система линейных уравненийМатрица
- 16. Методы последовательного исключения неизвестныхМетод ГауссаНад матрицами A
- 17. Последовательная программа// прямий хід//k- нумерує кроки виключення//i-
- 18. Распараллеливание прямого ходаСтроки распределяются по процессорам равномерно,
- 19. Реализация// прямий хід//k- нумерує кроки виключення//i- нумерує
- 20. Другие алгоритмы передачиОбычное кольцоМодифицированное кольцоДвойное кольцоМодифицированное двойноекольцо
- 21. Оценка времени передачиПоследовательный алгоритм – порядка n3
- 22. ИллюстрацияЭффективность растет при увеличении порядка матрицыОдин из самых эффективных методов
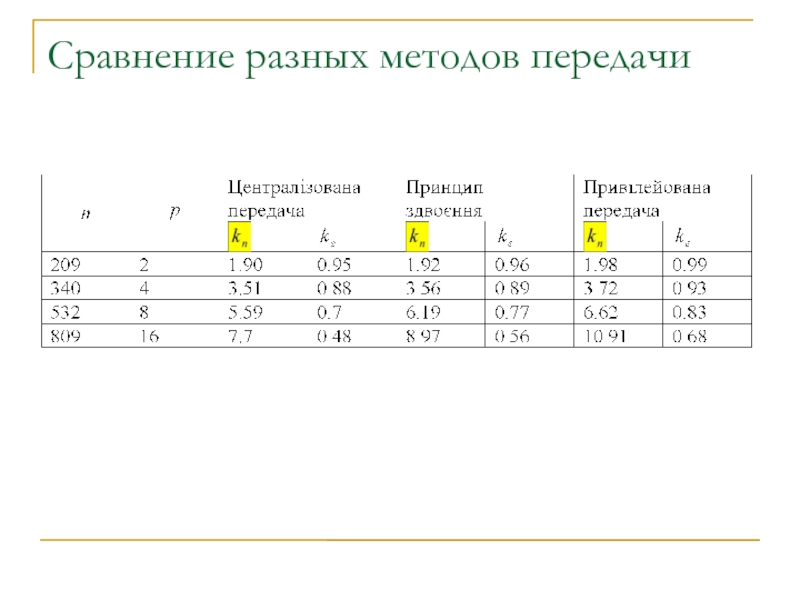
- 23. Сравнение разных методов передачи
- 24. Итеративные методыМетод Якоби выражается значение неизвестного через значения других неизвестныхИтеративно находятся все значения
- 25. Последовательный вариант//xnew – наступне наближення//xold – попереднє наближення//eps – умова завершення ітераційного процесуfor(;;){for(i=0;i
- 26. РаспараллеливаниеКаждый элемент нового приближения может быть вычислен
- 27. Параллельная реализацияfor(;;){for(i=c*n/p;i
- 28. Оценка времениВремя параллельных вычислений складывается из времени работы процессора и времени выполнения передачи
- 29. ИллюстрацияРаспараллеливается достаточно эффективноТребует синхронизации, что снижает эффективность
- 30. Сравнение различных матричных методов
- 31. Решение дифференциальных уравнений в частных производныхВозникают в различных физических задачахРасчет прогноза погодыРасчет тепловых свойствЭлектричествоРасчет прочности конструкцияАэродинамика
- 32. Дискретизация задачиНа область накладывается сетка с шагом hПроизводные заменяются разностными аппроксимациямиАналогично вторые производныеУравнениеhhij
- 33. Пример – уравнение ЛапласаВозникает в электротехнических задачахУравнение
- 34. Решение уравненияМетод ЯкобиВыражаем значение в узле сетки
- 35. РаспараллеливаниеНа сетку накладывается процессорная сеткаКаждому узлу процессорной
- 36. Реализация// px, py – координати процесора в
- 37. Оценка эффективностиДля сетки n2 время выполнение последовательного
- 38. Вопросы
- 39. Слайд 39
- 40. Скачать презентанцию
ПланНахождение суммы значенийУмножение матрицРешение систем линейных уравнений
Слайды и текст этой презентации
Слайд 1Распараллеливание некоторых численных методов
Судаков А.А.
“Параллельные и распределенные вычисления” Лекция 17
Слайд 3Сумма последовательности значений
Нахождение суммы большого количества слагаемых
Численное интегрирование
Суммирование рядов
Умножение векторов
Последовательный
вариант
Слайд 4Походы к распараллеливанию суммирования
Конвейеризация последовательности операций
Векторизация
Разбиение цикла на блоки
Слайд 5Разбиение цикла на блоки
Суммирование ассоциативно
Цикл разбивается на блоки
Каждый процессор выполняет
свой блок цикла параллельно с остальными
Результаты работы всех процессоров складываются
//
p – кількість процесорів// k – номер поточного процессора від 0 до p-1
// f() – підпрограма обчислення fi
sum=0;
for(i=k; i
}
reduce(0,sum);
Слайд 6Оценка количества операций
Время выполнения последовательного алгоритма
Nf – количество операций вычисления
функции
Время выполнения параллельного суммирования
Время передачи данных
Коэффициент ускорения
Слайд 7Эффективность распараллеливания суммирования
Коэффициент эффективности
Ускорение при распараллеливании будет когда
При большом
количестве процессоров
При увеличении количества процессоров эффективность падает
При увеличении количества процессорных
операций эффективность растет 
Слайд 8Конвейер
Количество пересылок равно p-1
Эффективность ниже, чем при число параллельной
обработке
Существует возможность выполнения асинхронных операций
Процессор, который закончил работу может сразу
же приступить к выполнению дальнейшей работыПроцессор 1
Начал выполнять
Дальнейшую работу
Процессор 2
Получил результат
Процессора 1,
выполнил суммирование
Передал дальше
Процессор 3
Получил результат
Процессора 2,
выполнил суммирование
Передал дальше
Слайд 9Графическая иллюстрация
Конвейер дает худшие результаты по ускорению, но не требует
синхронизации между всеми процессорами и можно уменьшит время простоя даже
для гетерогенной системы
Слайд 10Умножение матриц
Блочное представление дает возможность вычислять блок результата параллельно с
остальными блоками результата
Рассмотрим пример для квадратной сетки размерности k, блоков
размерности m и матрицы размерности n, количество процессоров p
Слайд 11Алгоритм Фокса
Каждый процессор pij вычисляет свой блок матрицы Cij
На каждом
процессоре выделяется место для хранения 4-х блоков
Cij – блок результата
Aij – блок матрицы A, который хранится на текущем процессоре
A1ij – блок матрицы A, который получен с другого процессора
B1ij – блок матрицы B, который получен с другого процессора (блоки правой матрицы все время перемещаются)
Выполняется инициализация
C – обнуляется
A – содержит блок матрицы A данного процессора
B1 – содержит блок матрицы B данного процессора
Слайд 12Алгоритм Фокса (продолжение)
На каждой итерации алгоритма, номер l (l=1,k)
Один процессор
каждой строки отправляет свой блок матрицы A на все процессоры
своей строки, номер столбца j для строки i=(i-l+1)mod(k)+1. Процессоры принимают эти данные в матрицу A1Выполняется обычное матричное умножение C=C+A1*B1
Матрица B1 передается соседу сверху
Повторяется для следующего l
Передача блоков
матрицы A
Передача блоков
матрицы B
Слайд 13Оценка времени Алгоритма Фокса
Время одной итерации равно
Время рассылки блока
матрицы A1
Время отправки блоков матрицы B1
Время умножения матриц A1 и
B1Время k итераций в k раз больше
Коэффициент ускорения
Слайд 14Характеристики
Алгоритм содержит как конвейерные так и параллельные операции
Достаточно эффективен при
больших размерностях матрицы
Существуют другие алгоритмы с большим количество синхронных или
асинхронных операций
Слайд 15Решение систем линейных уравнений
Есть система линейных уравнений
Матрица A размерности nxn
Матрицы
B и x размерности nxm
Матрица x - неизвестна
Слайд 16Методы последовательного исключения неизвестных
Метод Гаусса
Над матрицами A и B выполняются
элементарные преобразования, чтобы свести матрицу A к треугольному виду
После чего
решение находится с помощью обратного хода метода ГауссаИсключение неизвестных
В каждой строке выбирается ведущий элемент – самый большой по модулю
Текущая строка вычитается из всех расположенных ниже, нормированных на ведущий элемент
При этом на месте ведущего элемента во всех ниже расположенных строках будут нули
Слайд 17Последовательная программа
// прямий хід
//k- нумерує кроки виключення
//i- нумеує рядки
//j –
нумерує стовпці матриці A
//l – нумерує стовпці матриці B
for(k=0;k
i++){a[i][k]/=a[k][k];
// ділення на ведучий елемент
// виключення матриць A і B
for(j=k+1;j
}
}
//зворотній хід
for(i=n-1; i>=0; i--){
for(l=n;l
a[i][l]/=a[i][i];
}
}
Слайд 18Распараллеливание прямого хода
Строки распределяются по процессорам равномерно, каждый процессор содержит
n/p строк, i-й процессор содержит строки с номерами i+kp (k=1,n/p)
Передачу
лучше выполнить конвейерно по принципу привилегированной передачиПервый процессор находит ведущий элемент, вычисляет результат деления своей строки на ведущий элемент
Результат деления и номер ведущего элемента пересылается на следующий процессор
Первый процессор продолжает исключение своих строк
Второй процессор принимает данные от первого , выполняет исключение и тоже передает данные дальше
Процессор1
Ведущий элемент
Процессор1
Передача следующему
Процессор2
Процессор1
Исключение и передача
Процессор2
Слайд 19Реализация
// прямий хід
//k- нумерує кроки виключення
//i- нумерує рядки
//j – нумерує
стовпці матриці A
//l – нумерує стовпці матриці B
//p - кількість
процсорів//c – номер поточного процесора
//cur – поточний рядок
for(k=0;k
// поточний рядок у нас
cur=a[k];
} else {
//прийняти поточний рядок від попереднього в кільці
recv(c>0?c-1:p-1,cur);
}
//передати поточний рядок наступному в кільці
if(k
for(i=0;i
a[i][k]/=cur[k];
// виключення елементів матриць A і B
for(j=k+1;j
}
}
//зворотній хід
//кожен процессор має зберігати всі попередні
//значення x[i][l]
//кожен процесор виконує n/p виключень
for(i=n+c-p; i>=c; i-=p){
//отримуємо всі обраховані попередні значення x
for(j=(i+p)>(n-1)?(n-1):(i+p);j>i;j++){
//всі інші значення x вже отримані
recv(c
send(c>0?c-1:p-1,x[j]);
}
for(l=0;l
a[i][n+l]/=a[i][i];
x[i]=a[i]+n
// відправляємо обрахований рядок
if(i>0)
send(c>0?c-1:p-1,a[i]);
}
}
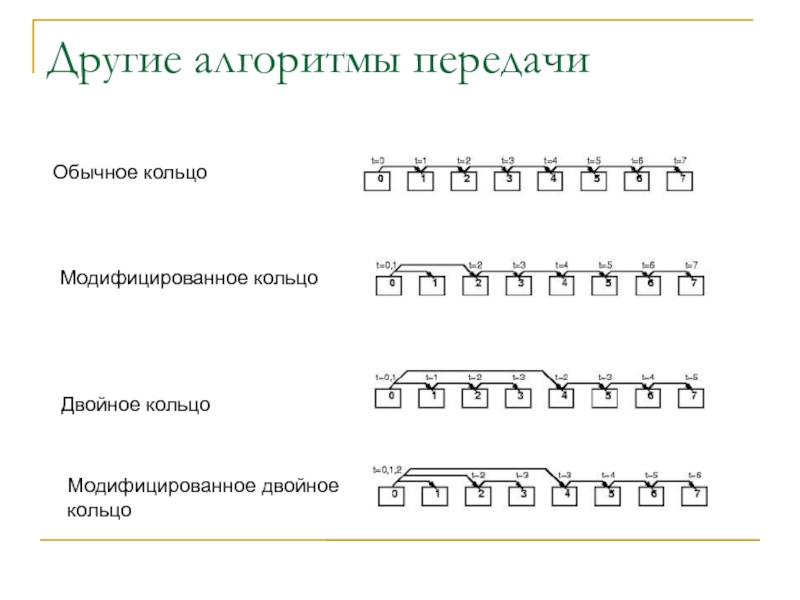
Слайд 20Другие алгоритмы передачи
Обычное кольцо
Модифицированное кольцо
Двойное кольцо
Модифицированное двойное
кольцо
Слайд 21Оценка времени передачи
Последовательный алгоритм – порядка n3 операций
Параллельный алгоритм
Порядка n3/p
последовательных операций
Порядка n2 последовательных пересылок данных
Порядка n устанослений связи
Слайд 22Иллюстрация
Эффективность растет при увеличении порядка матрицы
Один из самых эффективных методов
Слайд 24Итеративные методы
Метод Якоби выражается значение неизвестного через значения других неизвестных
Итеративно
находятся все значения
Слайд 25Последовательный вариант
//xnew – наступне наближення
//xold – попереднє наближення
//eps – умова
завершення ітераційного процесу
for(;;){
for(i=0;i
Слайд 26Распараллеливание
Каждый элемент нового приближения может быть вычислен параллельно с другими
элементами этого же приближения
Каждый процессор содержит n/p=q строк матрицы A
Каждый
процессор вычисляет свою часть приближенияКаждый процессор передает всем остальным свою часть приближения
Слайд 28Оценка времени
Время параллельных вычислений складывается из времени работы процессора и
времени выполнения передачи
Слайд 29Иллюстрация
Распараллеливается достаточно эффективно
Требует синхронизации, что снижает эффективность
Слайд 31Решение дифференциальных уравнений в частных производных
Возникают в различных физических задачах
Расчет
прогноза погоды
Расчет тепловых свойств
Электричество
Расчет прочности конструкция
Аэродинамика
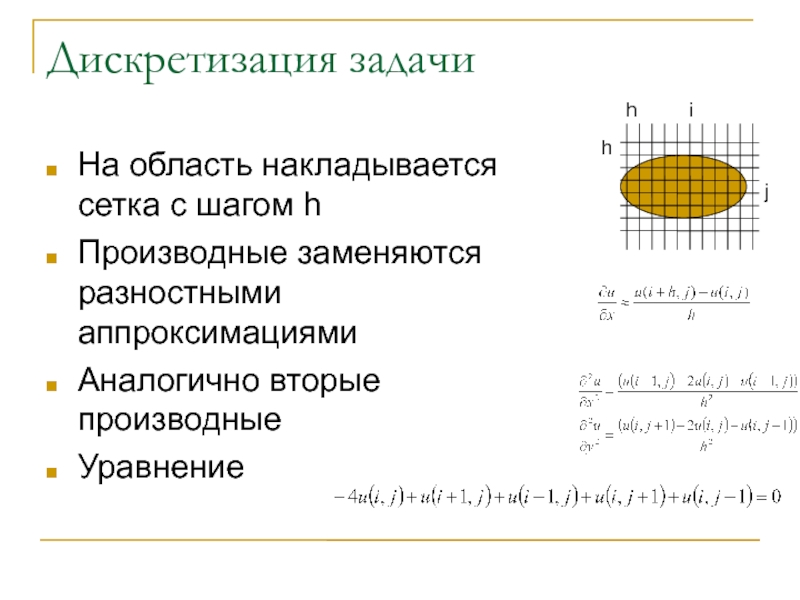
Слайд 32Дискретизация задачи
На область накладывается сетка с шагом h
Производные заменяются разностными
аппроксимациями
Аналогично вторые производные
Уравнение
h
h
i
j
Слайд 33Пример – уравнение Лапласа
Возникает в электротехнических задачах
Уравнение Лапласа
Граничные условия
Найти потенциал
электрического поля в области с цилиндрической симметрией
На границе области потенциал
равен f(x,y)U(x,y)
F(x,y)
Слайд 34Решение уравнения
Метод Якоби
Выражаем значение в узле сетки через 4 соседних
значения
Выбираем начальное приближение в узле
Интеративно повторяем до сходимости
(I,j)
(I+1,j)
(I-1,j)
(I,j-1)
(I,j+1)
Слайд 35Распараллеливание
На сетку накладывается процессорная сетка
Каждому узлу процессорной сетки соответствует n/p
узлов сетки дискретизации
Для каждого узла процессорной сетки итерации можно проводить
параллельноПосле итерации необходим обмен на границе сетки
2
4
3
Узел
процессорной
сетки
Узел сетки
дискретизации
Слайд 36Реализация
// px, py – координати процесора в процесорній сітці
// u
– старі наближення функції у вузлах сітки
// unew – нові
наближення функції у вузлах сіткиfor(;;){
if(px!=0) for(j=0;j
}
}
//передати на всі процесори норму нового наближення
allreduce(abs(unew));
if(abs(abs(unew)-abs(u))< eps) break;
u=unew;
absu=abs(unew);
}
Слайд 37Оценка эффективности
Для сетки n2 время выполнение последовательного алгоритма 4tn2
Для p2
процессоров время состоит из процессорной работы и обмена
ускорение растет с
увеличением количества данных задачи и падает с увеличением количества процессоров
