Распознаватели регулярных языков

АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Кафедра ТК

Тема: Распознаватели регулярных языков

автоматы без внешней памяти –

конечные автоматы (КА).

M(Q, V, δ, q0, F),

где Q – конечное множество состояний автомата;

V – конечное множество допустимых входных символов
(алфавит автомата);

– функция переходов, отображающая V×Q (декартово произведение множеств) в множество подмножеств Q: R(Q),
то есть δ(a,q)=R, a∈V, q∈Q, R⊆Q;

q0 – начальное состояние автомата Q, q0∈Q;

F – непустое множество конечных состояний автомата, F⊆Q, F≠∅.

Конечный автомат является полностью определенным, если в каждом его состоянии существует функция перехода для всех возможных входных символов, то есть
∀a∈V, ∀q∈Q ∃ δ(a, q)=R, R⊆Q.

(тактов).
На каждом шаге работы автомат находится в одном из

своих состояний Q (в текущем состоянии), на следующем шаге он может перейти в другое состояние или остаться в текущем состоянии.

То, в какое состояние автомат перейдет на следующем шаге работы, определяет функция переходов δ (зависит не только от текущего состояния, но и от символа из алфавита V, поданного на вход автомата).

Когда функция перехода допускает несколько следующих состояний автомата, то КА может перейти в любое из этих состояний.

В начале работы автомат всегда находится в начальном состоянии q0.

Работа КА продолжается до тех пор, пока на его вход поступают символы из входной цепочки ω∈V+.

определяется в виде:

(q, ω, n),
где q – текущее состояние автомата, q∈Q;
ω – цепочка входных символов, ω∈V+;
n – положение указателя в цепочке символов, n∈N∪{0}, n≤|ω| (N – множество натуральных чисел).

Конфигурация КА на следующем шаге работы определяется в виде:
(q', ω, n+l),

где q'∈δ(a, q), а символ a∈V находится в позиции n+1 цепочки ω.

Начальная конфигурация КА: (q0, ω, 0);
Заключительная конфигурация КА: (f, ω, n), f∈Q, n=|ω|,
она является конечной конфигурацией, если f∈F.

Конечный автомат принимает цепочку символов ω∈V+, если, получив на вход эту цепочку, он из начального состояния q0 может перейти в одно из конечных состояний f∈F, иначе КА не принимает цепочку символов.

образом:
начальное состояние – дополнительной пунктирной линией,
конечное состояние –

дополнительной сплошной линией.

Системное программное обеспечение

Распознаватели регулярных языков

Граф переходов КА – это направленный помеченный граф, с символами состояний КА в вершинах, в котором есть дуга (p, q) p, q∈Q, помеченная символом a∈V, если в КА определена функция перехода δ(а, р) и q∈δ(a, p).

Пример: конечный автомат: M({H, A, B, S},{a, b, с}, δ, H,{S});

δ:
δ(a, H)=A; δ(c, H)=B; δ(a, A)=B; δ(c, A)=B; δ(b, B)=A; δ(b, B)=S.

a

c

a, c

b

b

Для моделирования работы КА его нужно привести к полностью определенному виду, чтобы исключить ситуации, из которых нет переходов по входным символам.
С этой целью в КА добавляется еще одно состояние, которое условно называется «ошибка» (на это состояние замыкают все неопределенные переходы, а все переходы из самого состояния «ошибка» замыкают на него же).

b

b

a, c

a, b, c

a, b, c

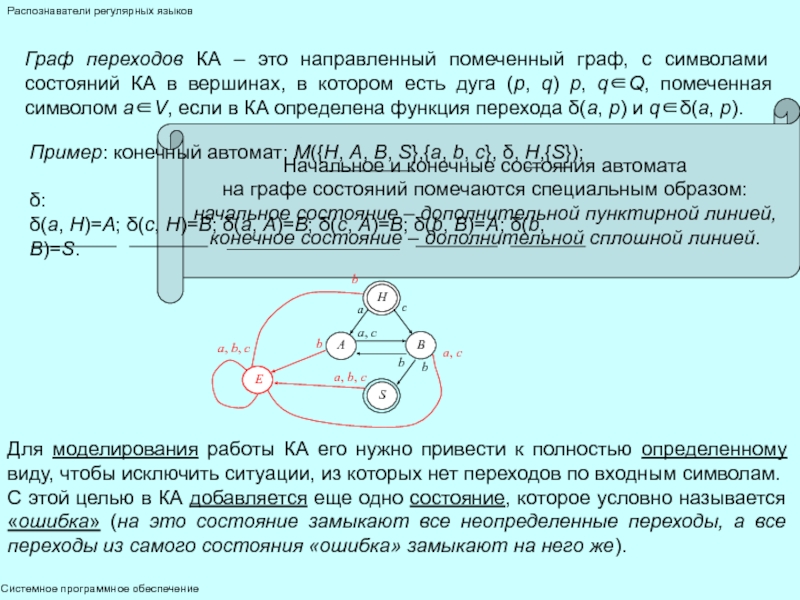
в каждом из его состояний для любого входного символа функция

перехода содержит не более одного состояния: ∀a∈V, ∀q∈Q: либо δ(a, q)={r}, r∈Q, либо δ(a, q)=∅.

При построении компиляторов чаще всего
используют полностью определенный
детерминированный конечный автомат.

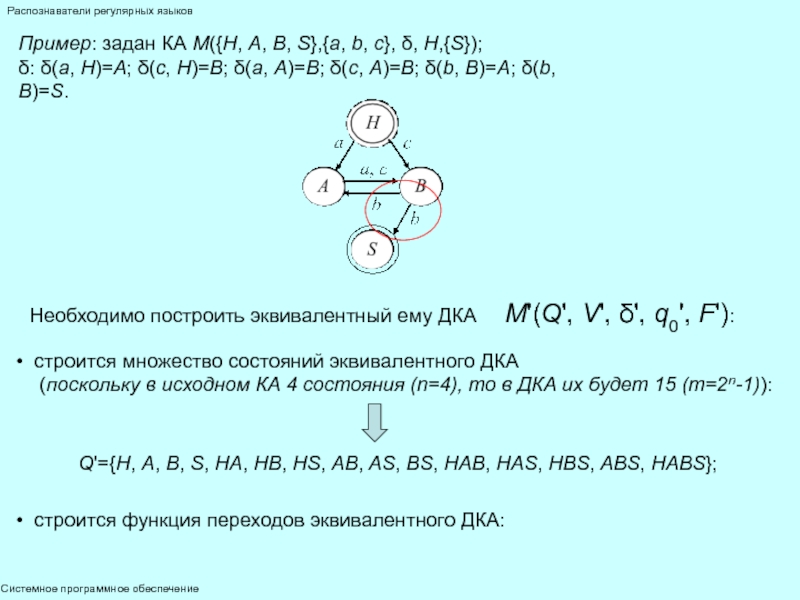
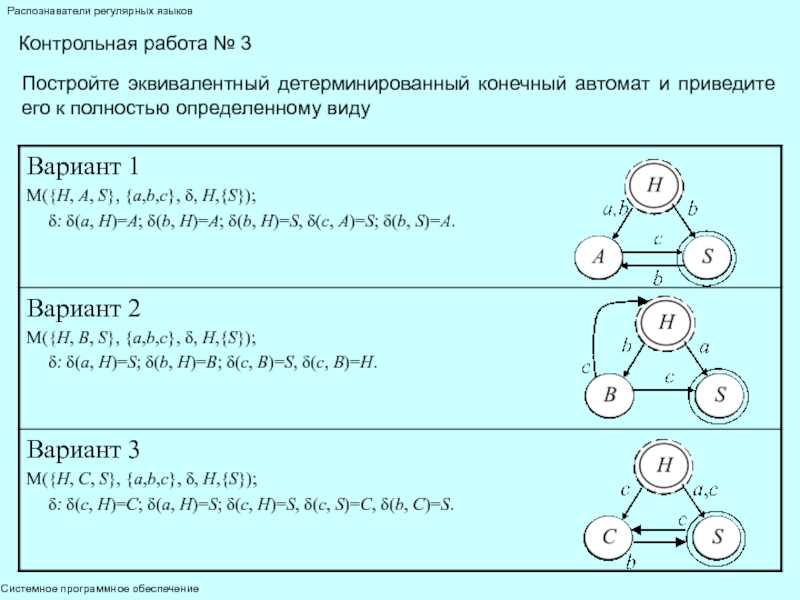
Алгоритм преобразования произвольного КА (M(Q, V, δ, q0, F)) в эквивалентный ему ДКА (M'(Q', V', δ', q0', F ')):

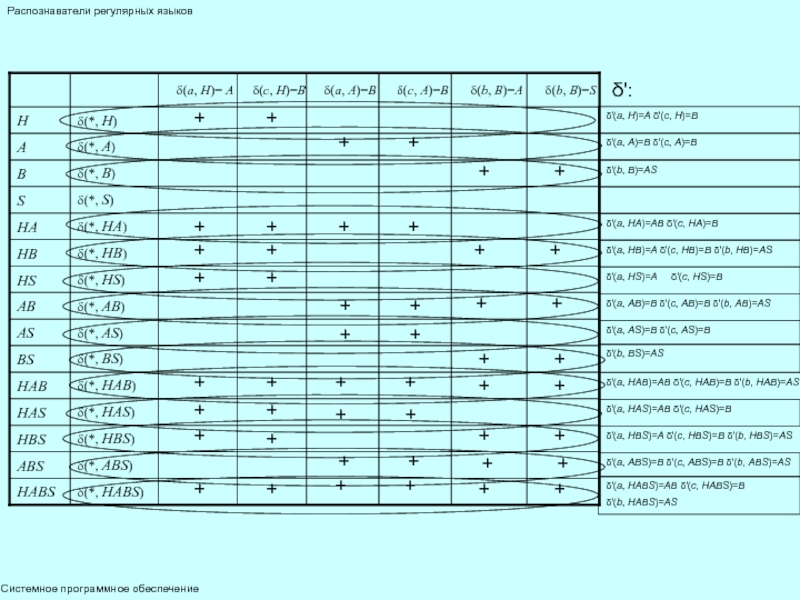
множество состояний Q' автомата М' строится из комбинаций всех состояний множества Q автомата М:
если q1, q2, …, qn, n>0 – состояния автомата M, 0 то всего будет 2n-1 состояний автомата М': [q1, q2, …, qm], 0

функция переходов δ' автомата М' строится так:
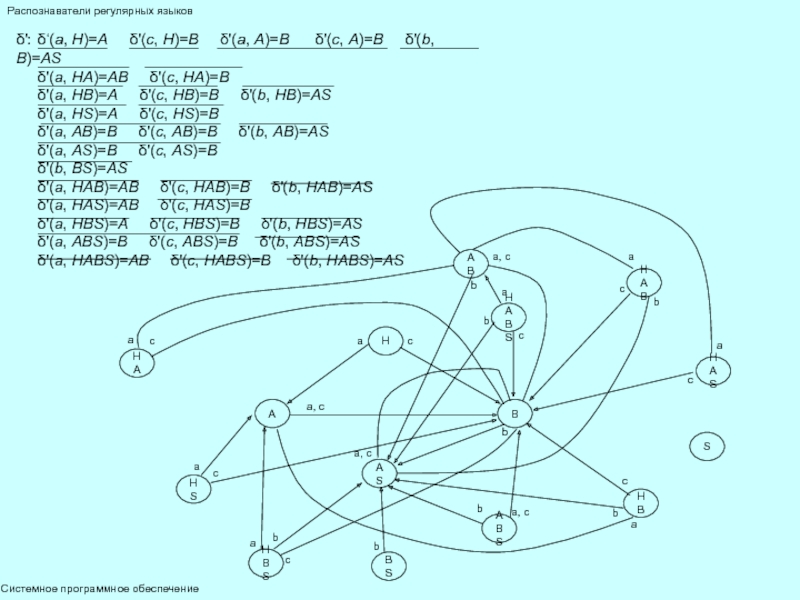
δ'(a, [q1, q2, …, qm])=[r1, r2, …, rk], где ∀0

q'0=[q0];

если f1, f2, …, fl, l>0 – конечные состояния автомата М, 0 тогда множество конечных состояний F' автомата М' строится из всех
состояний, имеющих вид […, fi,…], fi∈F.

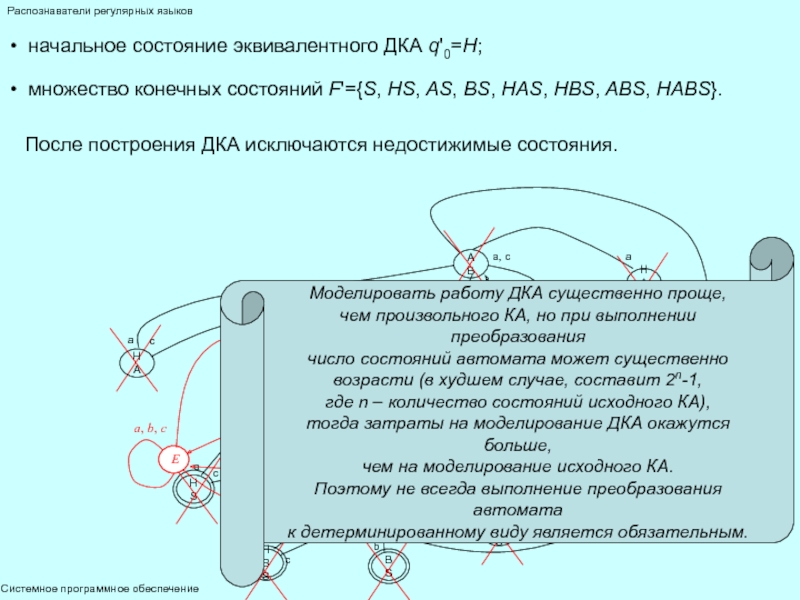
После построения из ДКА необходимо удалить все недостижимые состояния – ни при какой входной цепочке ω∈V+ невозможен переход автомата из начального состояния q0 в состояние q.

S},{a, b, с}, δ, H,{S});
δ: δ(a, H)=A; δ(c, H)=B; δ(a,

A)=B; δ(c, A)=B; δ(b, B)=A; δ(b, B)=S.

Необходимо построить эквивалентный ему ДКА M'(Q', V', δ', q0', F'):

строится множество состояний эквивалентного ДКА
(поскольку в исходном КА 4 состояния (n=4), то в ДКА их будет 15 (m=2n-1)):

Q'={Н, А, В, S, НА, НВ, HS, АВ, AS, BS, НАВ, HAS, HBS, ABS, HABS};

строится функция переходов эквивалентного ДКА:

δ'(c, A)=B
δ'(b, B)=AS

δ'(a, НА)=AB δ'(c, НА)=B
δ'(a, НB)=A

δ'(c, НB)=B δ'(b, НB)=AS

δ'(a, HS)=A δ'(c, HS)=B

δ'(a, АВ)=B δ'(c, АВ)=B δ'(b, АВ)=AS

δ'(b, BS)=AS

δ'(a, НАВ)=AB δ'(c, НАВ)=B δ'(b, НАВ)=AS

δ'(a, HAS)=AB δ'(c, HAS)=B

δ'(a, HBS)=A δ'(c, HBS)=B δ'(b, HBS)=AS

δ'(a, ABS)=B δ'(c, ABS)=B δ'(b, ABS)=AS

δ'(a, HABS)=AB δ'(c, HABS)=B
δ'(b, HABS)=AS

δ'(a, AS)=B δ'(c, AS)=B

δ':

H)=B δ'(a, A)=B δ'(c, A)=B

δ'(b, B)=AS
δ'(a, НА)=AB δ'(c, НА)=B
δ'(a, НB)=A δ'(c, НB)=B δ'(b, НB)=AS
δ'(a, HS)=A δ'(c, HS)=B
δ'(a, АВ)=B δ'(c, АВ)=B δ'(b, АВ)=AS
δ'(a, AS)=B δ'(c, AS)=B
δ'(b, BS)=AS
δ'(a, НАВ)=AB δ'(c, НАВ)=B δ'(b, НАВ)=AS
δ'(a, HAS)=AB δ'(c, HAS)=B
δ'(a, HBS)=A δ'(c, HBS)=B δ'(b, HBS)=AS
δ'(a, ABS)=B δ'(c, ABS)=B δ'(b, ABS)=AS
δ'(a, HABS)=AB δ'(c, HABS)=B δ'(b, HABS)=AS

Н

А

В

S

AB

HА

HВ

HS

AS

HАB

HВS

BS

HAS

AВS

HAВS

a

c

a, c

b

a

c

b

c

c

c

b

b

a

a

a, c

a, c

a

b

a

c

a

c

b

a, c

b

a

c

b

состояние эквивалентного ДКА q'0=Н;

множество конечных состояний F'={S, HS, AS,

BS, HAS, HBS, ABS, HABS}.

После построения ДКА исключаются недостижимые состояния.

a, c

a, b, c

b

b

b

a, c

Моделировать работу ДКА существенно проще,
чем произвольного КА, но при выполнении преобразования
число состояний автомата может существенно
возрасти (в худшем случае, составит 2n-1,
где n – количество состояний исходного КА),
тогда затраты на моделирование ДКА окажутся больше,
чем на моделирование исходного КА.
Поэтому не всегда выполнение преобразования автомата
к детерминированному виду является обязательным.

заключается в построении эквивалентного КА с меньшим числом состояний.
Для минимизации

КА используется алгоритм построения эквивалентных состояний КА.

Множества эквивалентных состояний автомата называются классами эквивалентности, а вся их совокупность – множеством классов эквивалентности R(n) причем R(0)={F, Q-F}.

0-эквивалентными состояниями автомата M(Q, V, δ, q0, F) являются два множества его состояний: F и Q-F.

Два различных состояния в КА M(Q, V, δ, q0, F) q∈Q и q'∈Q называются n-эквивалентными (n-неразличимыми), n≥0 n∈N∪{0}, если, находясь в одном из этих состояний и получив на вход любую цепочку символов ω: ω∈V* |ω|≤n, автомат может перейти в одно и то же множество конечных состояний.

Алгоритм минимизации КА:
из автомата исключаются все недостижимые состояния;
строятся классы эквивалентности автомата;
классы эквивалентности состояний исходного КА становятся
состояниями результирующего минимизированного КА;
функция переходов результирующего КА очевидным образом
строится на основе функции переходов исходного КА.

конечный автомат и приведите его к полностью определенному виду