Слайд 2Лекция 13. РАСПРЕДЕЛЕНИЕ ГАЗОВЫХ МОЛЕКУЛ ПО СКОРОСТЯМ И ЭНЕРГИЯМ
1. Скорость
газовых молекул. Опыт Штерна.
2. Вероятность события. Понятие о распределении молекул
газа по скоростям.
3. Функция распределения Максвелла.
4. Барометрическая формула.
5. Распределение Больцмана.
6. Закон распределения Максвелла-Больцмана.
7. Распределение Бозе-Эйнштейна, Ферми-Дирака.
Слайд 31. Скорости газовых молекул. Опыт Штерна.
Поставьте себя на место исследователей
60-х годов позапрошлого столетия. Сформулирована молекулярно-кинетическая теория, но нет никаких
доказательств существования самих молекул! А вся теория базируется на предположении о движении молекул. С какой они движутся скоростью? И как эту скорость измерить, если молекулы невидимы.
Теоретики первыми нашли выход. Из уравнения молекулярно-кинетической теории газов известно, что
(13.1)
Слайд 4
(13.2)
Получена хорошая формула, но масса молекулы неизвестна! Тогда можно записать:
(13.3)
А
мы знаем, что
, тогда
(13.4)
где р – давление; ρ − плотность. Они уже измеряемые величины.
Слайд 5 Например: плотность азота (N2) равна 1,25 кг/м3 при Т=0°С и
р=1 атм, υN2=500 м/c. Для водорода: υH2=2000 м/c.
При этом, интересно
отметить, что скорости молекул в газе близки к скорости звука в этом газе. Это объясняется тем, что звуковые волны переносятся молекулами газа. И неудивительно поэтому, что
Слайд 6 Экспериментально впервые скорости молекул были измерены в 1920 г. Штерном.
За этот опыт и за большой вклад в развитие молекулярной
физики в 1943 г. он был удостоен Нобелевской премии.
В этом опыте были не только измерены скорости газовых молекул, но и показано, что они имеют большой разброс по скоростям. Причина, в хаотичности теплового движения молекул. Ещё в XIX веке Максвелл утверждал, что молекулы беспо-рядочно сталкиваясь друг с другом как-то «распре-деляются» по скоростям, причём вполне опреде-лённым образом.
CCодержание
Слайд 72. Вероятность события. Понятие о распределении молекул газа по скоростям
Математическое
определение вероятности: вероятность какого-либо события – это предел, к которому
стремится отношение числа случаев, приводящих к осуществлению события, к общему числу случаев, при бесконечном увеличении последних. Или
(13.5)
где n′ − число опытов, когда событие произошло, а n − общее число опытов.
Слайд 8 Отсюда следует, что Р может быть от нуля до единицы
(Р=0÷1). Или по определению Лапласа: вероятность – отношение числа благоприятных
случаев к числу возможных случаев.
Определить распределение молекул по скоростям вовсе не значит, что нужно определить число молекул, обладающих той, или иной заданной скоростью. Ибо число молекул, приходящихся на долю каждого значения скорости равно нулю (постарайтесь это понять). Вопрос должен быть поставлен так: «Сколько молекул обладает скоростями, лежащими в этом интервале, включающем заданную скорость?» Так всегда ставятся статистические задачи.
Слайд 9 Например: на переписи населения, когда указывается возраст (20 лет) –
это не значит, что 20 лет, 0 часов, 0 минут,
а эта цифра свидетельствует, что возраст лежит в интервале от 20 лет до 21 года.
Итак, молекулы хаотически движутся. Среди них есть и очень быстрые и очень медленные. Благодаря беспорядочному движению и случайному характеру их взаимных столкновений, молекулы определённым образом распределяются по скоростям.
Это распределение оказывается однозначным и единственно возможным, и не только не противоречит хаотическому движению, но именно им и обусловлено.
Слайд 10 Мы будем искать число частиц (∆n), скорости которых лежат в
определённом интервале значения скорости ∆υ (от υ до υ+∆υ). То
есть ∆n – число благоприятных молекул.
Очевидно, что в единице объёма число таких благоприятных молекул тем больше, чем больше ∆υ.
Ясно так же, что ∆n должно быть пропорционально концентрации молекул (n). ∆n зависит и от самой скорости, так как в одинаковых по величине интервалах, но при разных абсолютных значениях скорости, число молекул будет различным (сложная фраза с простым смыслом: неодинаково, например, число людей в возрасте от 20 лет до 21 года и от 90 лет до 91 года).
(13.6)
или перейдя к пределу
dn=nf(υ)dυ,
(13.7)
где f(υ) – функция распределения.
Трудность вычисления (13.7) – в нахождении именно f(υ). Физический смысл f(υ) в том, что это отношение числа молекул, скорости которых лежат в определенном интервале скоростей, к общему числу молекул в единичном интервале скоростей: dv = 1, т.е.
(13.8)
Таким образом, f(υ) – имеет смысл вероятности. То есть f(υ) показывает, какова вероятность любой
Слайд 12молекулы газа в единице объёма иметь скорость, заключённую в единичном
интервале, включающем заданную скорость υ. В этом случае f(υ) называют
плотностью вероятности.
3. Функция распределения Максвелла
Мы воспользуемся результатами этого вывода. Скорость – векторная величина. Для x-ой составляющей скорости dnx= nf(υx)dυx, тогда
(13.8)
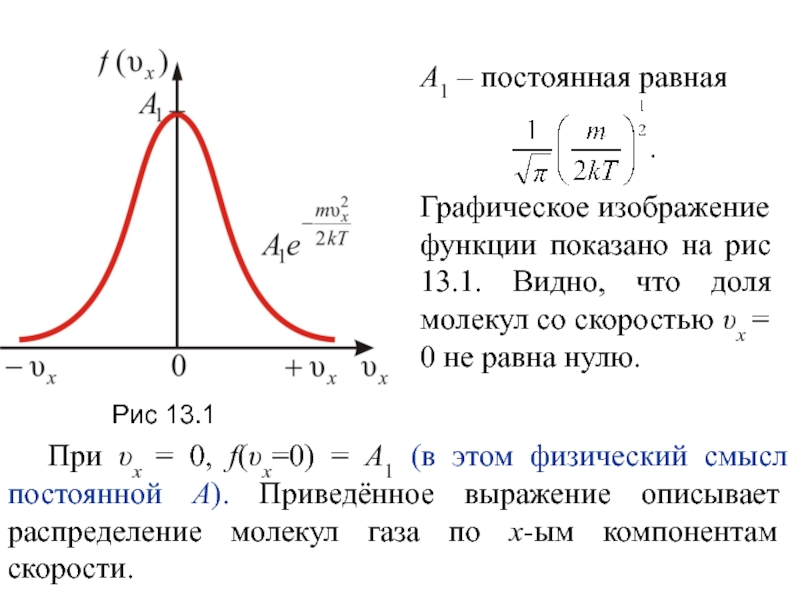
Слайд 13А1 – постоянная равная
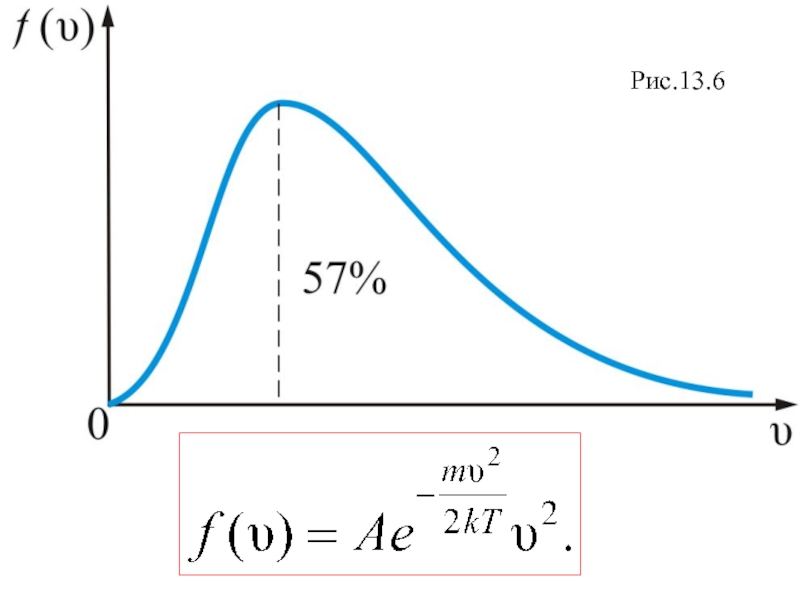
Графическое изображение функции показано на рис 13.1.
Видно, что доля молекул со скоростью υх = 0 не
равна нулю.
При υх = 0, f(υх=0) = А1 (в этом физический смысл постоянной А). Приведённое выражение описывает распределение молекул газа по x-ым компонентам скорости.
Рис 13.1
Слайд 14 Очевидно, что и
Вероятность того, что скорость молекулы одновременно удовлетворяет трём
условиям: x – компонента скорости лежит в интервале от υх
до υх + dυх; y – компонента, в интервале от υy до υy + dυy; z – компонента, в интервале от υz до υz + dυz будет равна произведению вероятностей каждого из условий (событий) в отдельности!
Слайд 15То есть
(13.9)
Этой формуле можно дать геометрическое истолкование: dnxyz – это
число молекул в паралле-лепипеде со сторонами dυx, dυy, dυz, то
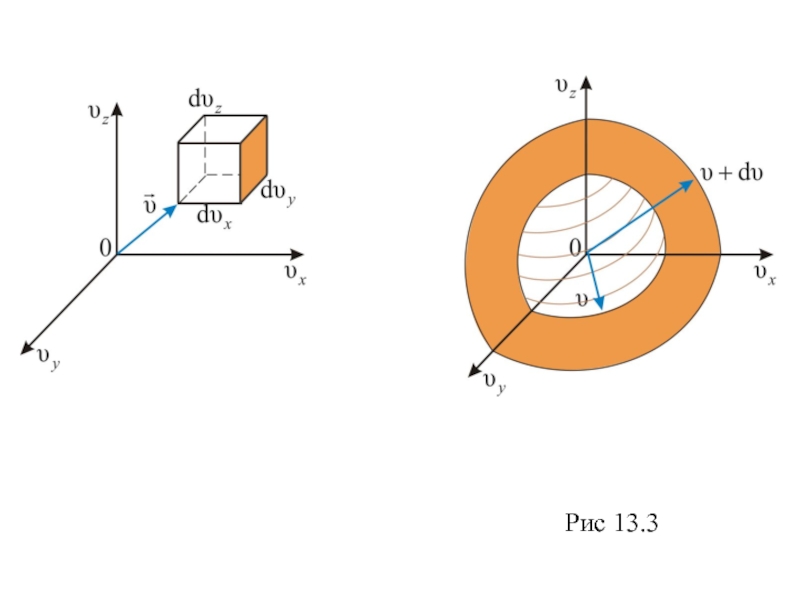
есть в объёме dV = dυxdυydυz, находящемся на расстоянии от начала координат в пространстве скоростей. Эта величина (dnxyz) не может зависеть от направления вектора скорости. Поэтому надо получить функцию распределения молекул по скоростям независимо от их направления, то есть по абсолютному значению скорости.
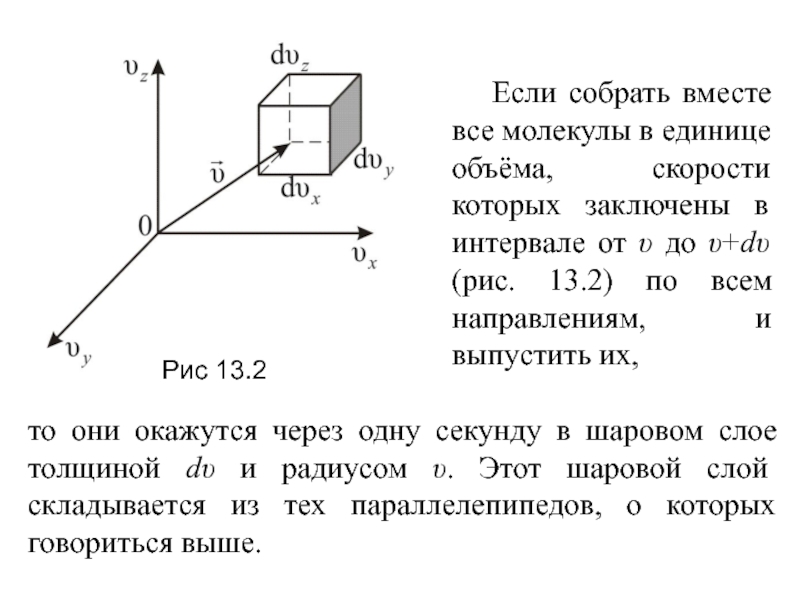
Слайд 16 Если собрать вместе все молекулы в единице объёма, скорости которых
заключены в интервале от υ до υ+dυ (рис. 13.2) по
всем направлениям, и выпустить их,
то они окажутся через одну секунду в шаровом слое толщиной dυ и радиусом υ. Этот шаровой слой складывается из тех параллелепипедов, о которых говориться выше.
Рис 13.2
Слайд 19 Объём этого шарового слоя
dΩ = 4πυ2dυ,
(13.10)
тогда общее число молекул в слое
(13.11)
Слайд 20 Отсюда следует закон Максвелла – распределение молекул по абсолютным значениям
скоростей:
(2.3.3)
где – доля всех частиц единичного объёма, скорости которых лежат в интервале от υ до
Слайд 21 При получаем плотность вероятности,
или функцию распределения молекул по скоростям:
(2.3.4)
Эта функция обозначает долю молекул единичного объёма газа, абсолютные скорости которых заключены в единичном интервале скоростей, включающем данную скорость.
тогда,
из (2.3.4) получим:
(2.3.5)
График этой функции показан на рис. 2.6.
Слайд 241) Вид физического распределения для каждого газа зависит от рода
газа (m) и от параметра состояния (Т). Давление р и
объём газа V на распределение молекул не влияют.
2) В показателе степени стоит отношение кинетической энергии, соответствующей данной скорости υ к (kТ) – средней кинетической энергии молекул при данной температуре.
Слайд 25Значит распределение Максвелла характеризует распределение молекул по значениям кинетической энергии
(то есть показывает, какова вероятность при данной температуре иметь именно
такое значение кинетической энергии).
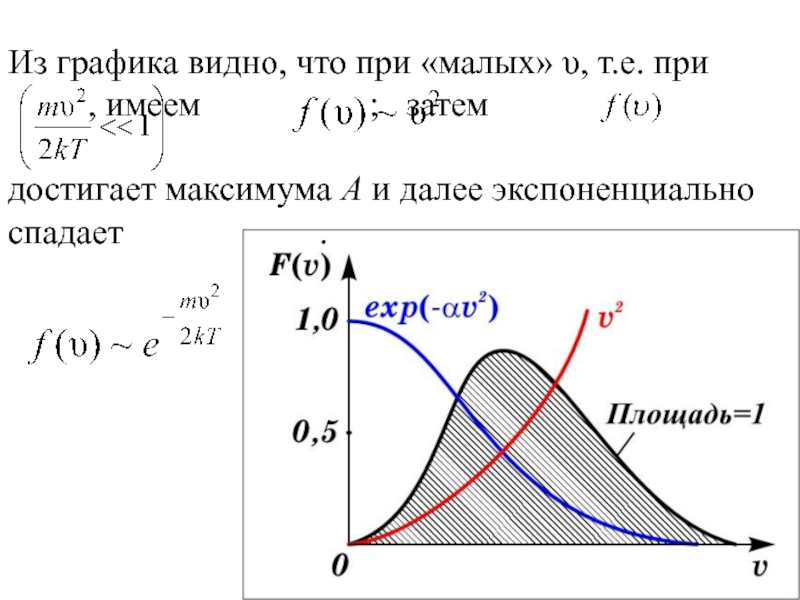
Слайд 26Из графика видно, что при «малых» υ, т.е. при
, имеем
; затем
достигает максимума А и далее экспоненциально спадает .
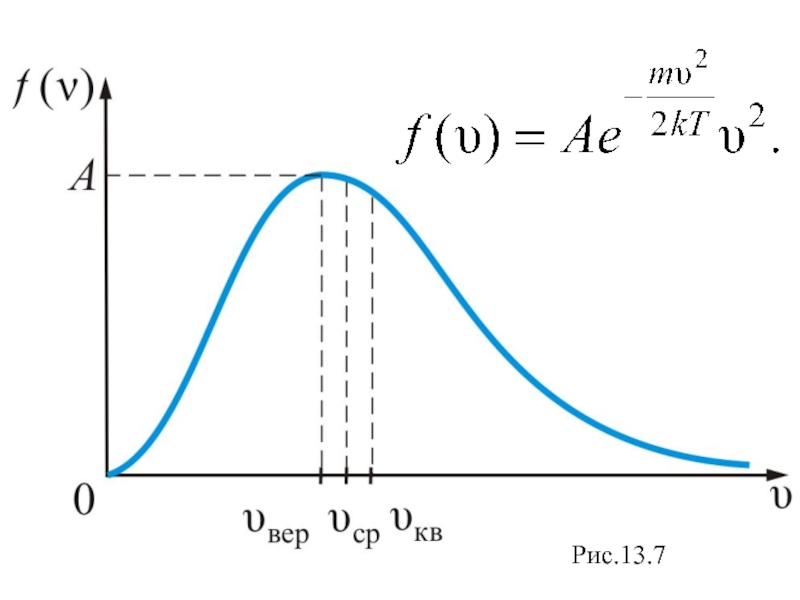
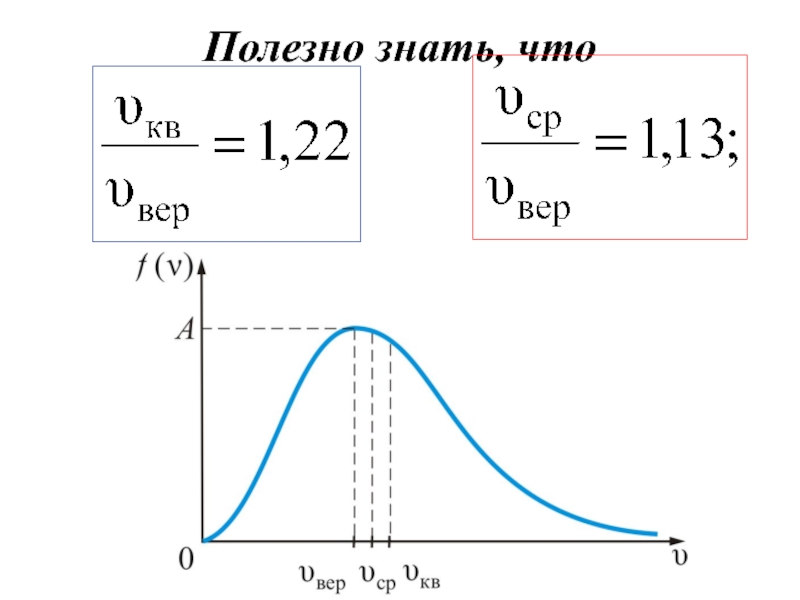
Слайд 27Наиболее вероятная, средне квадратичная и средняя арифметическая скорости молекул газа
Рассмотрим,
как изменяется с абсолютной величиной скорости число частиц, приходящихся на
единичный интервал скоростей, при единичной концентрации частиц.
График функции распределения Максвелла приведен на рис. 13.7.
Слайд 29Скорость, соответствующая максимуму распределения есть наиболее вероятная скорость (рис. 13.7).
Величину этой скорости найдем из условия равенства нулю производной
Слайд 30 Среднюю квадратичную скорость найдем используя соотношение
Тогда
Слайд 31Средняя арифметическая скорость − υср
(13.20)
где nf(υ)dυ=dn – число молекул
со скоростью от υ до υ+dυ. Если подставить сюда f(υ)
и вычислить, то:
– для одной молекулы.(13.21)
– для одного моля газа (13.22)
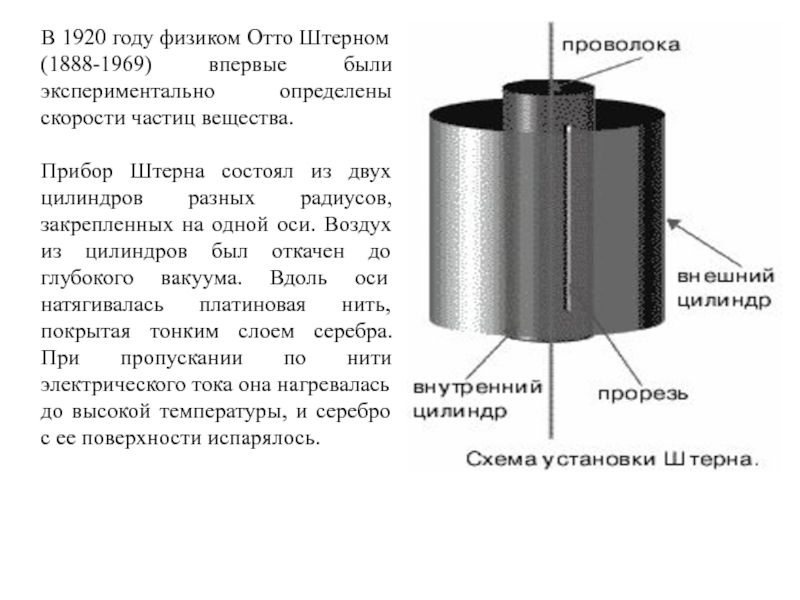
Слайд 34В 1920 году физиком Отто Штерном (1888-1969) впервые были экспериментально
определены скорости частиц вещества.
Прибор Штерна состоял из двух цилиндров разных
радиусов, закрепленных на одной оси. Воздух из цилиндров был откачен до глубокого вакуума. Вдоль оси натягивалась платиновая нить, покрытая тонким слоем серебра. При пропускании по нити электрического тока она нагревалась до высокой температуры, и серебро с ее поверхности испарялось.
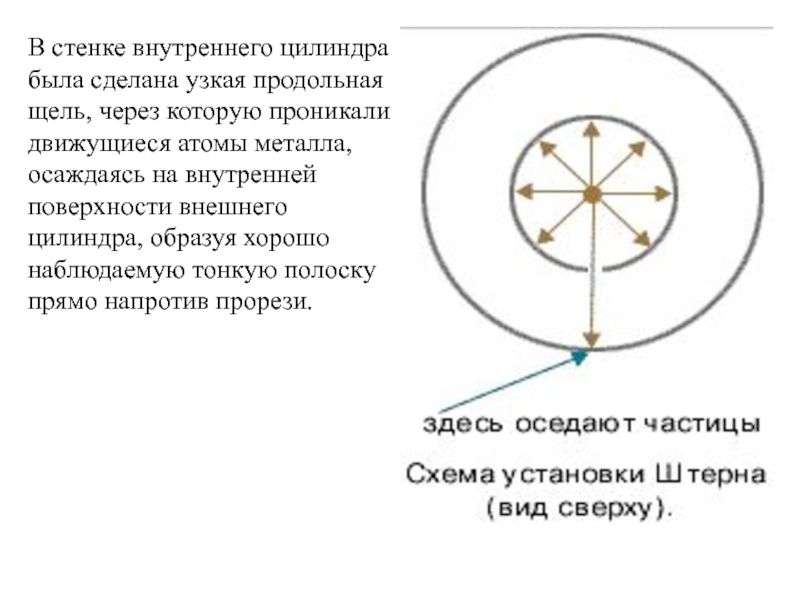
Слайд 35В стенке внутреннего цилиндра была сделана узкая продольная щель, через
которую проникали движущиеся атомы металла, осаждаясь на внутренней поверхности внешнего
цилиндра, образуя хорошо наблюдаемую тонкую полоску прямо напротив прорези.
Слайд 36
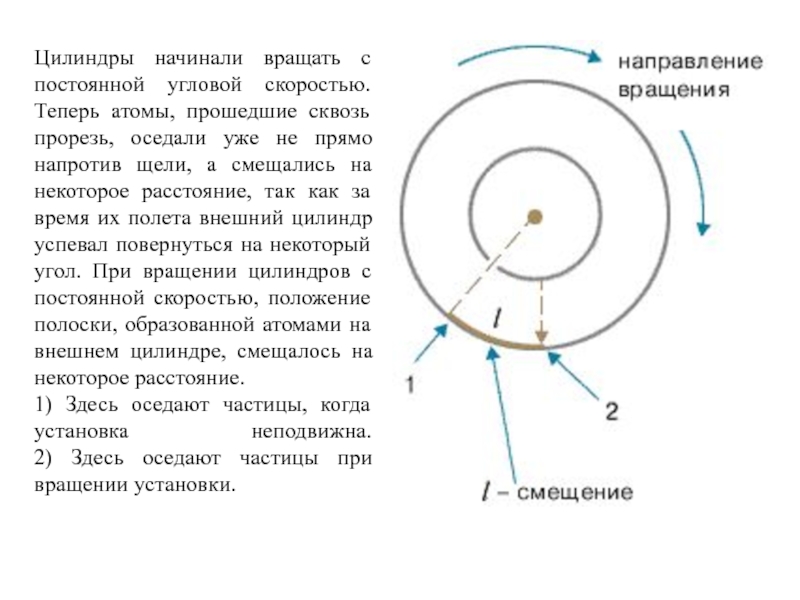
Цилиндры начинали вращать с постоянной угловой скоростью. Теперь атомы, прошедшие
сквозь прорезь, оседали уже не прямо напротив щели, а смещались
на некоторое расстояние, так как за время их полета внешний цилиндр успевал повернуться на некоторый угол. При вращении цилиндров с постоянной скоростью, положение полоски, образованной атомами на внешнем цилиндре, смещалось на некоторое расстояние.
1) Здесь оседают частицы, когда установка неподвижна.
2) Здесь оседают частицы при вращении установки.
Слайд 37Зная величины радиусов цилиндров, скорость их вращения и величину смещения
легко найти скорость движения атомов.
Время полета атома t от
прорези до стенки внешнего цилиндра можно найти, разделив путь, пройденный атомом и равный разности радиусов цилиндров, на скорость атома v. За это время цилиндры повернулись на угол "ФИ", величину которого найдем, умножив угловую скорость "ОМЕГА" на время t. Зная величину угла поворота и радиус внешнего цилиндра R2, легко найти величину смещения L и получить выражение, из которого можно выразить скорость движения атома.
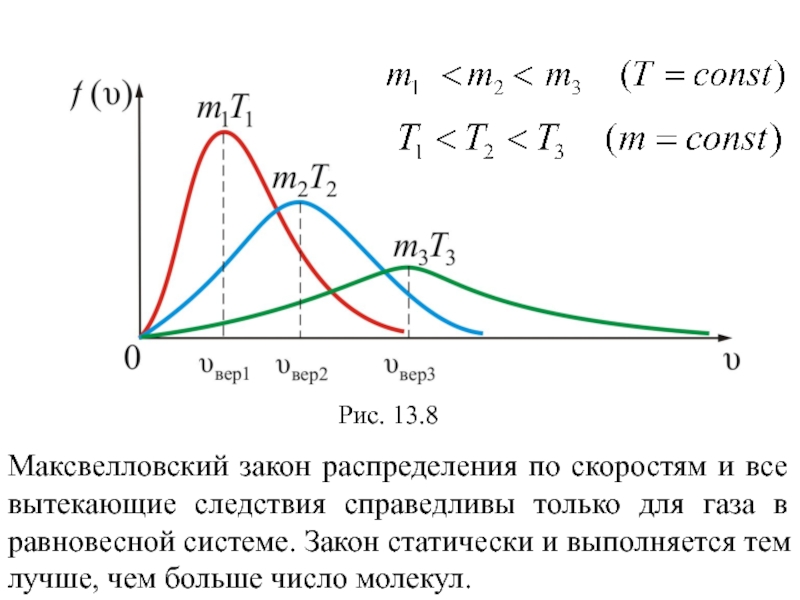
Слайд 41Зависимость функции распределения Максвелла от массы и температуры газа
Если у
нас смесь газов, то в пределах каждого сорта газа будет
своё распределение со своим m
Можно проследить за изменением f(υ) при изменении m и T: m1>m2>m3 (T = const) или T1 > T2 > T3 (m = const) (рис. 13.8). Площадь под кривой f(υ)=const=1 поэтому важно знать как будет изменяться положение максимума кривой.
Слайд 42Максвелловский закон распределения по скоростям и все вытекающие следствия справедливы
только для газа в равновесной системе. Закон статически и выполняется
тем лучше, чем больше число молекул.
Рис. 13.8
Слайд 43Формула Максвелла для относительных скоростей
Для решения многих задач удобно использовать
формулу Максвелла, где скорость выражена в относительных единицах. Относительная скорость
(13.23)
(13.24)
Это
уравнение универсальное. В таком виде функция распределения не зависит ни от рода газа ни от температуры.