Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
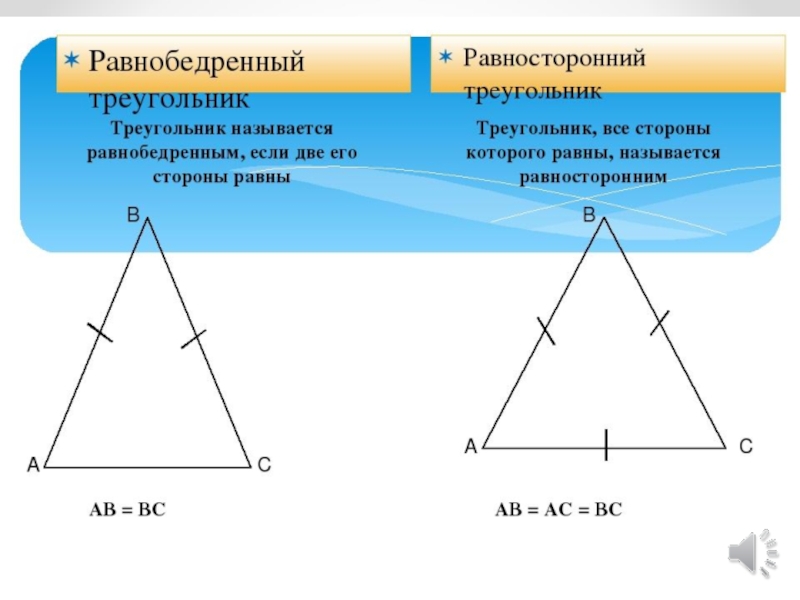
Равнобедренный треугольник
Содержание
- 1. Равнобедренный треугольник
- 2. Слайд 2
- 3. Свойства равнобедренного треугольника BAC
- 4. ABCDДоказательство:1) Проведём биссектрису AD треугольника АВС.2) Рассмотрим ∆ABD и ∆ACD: 12 Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников).
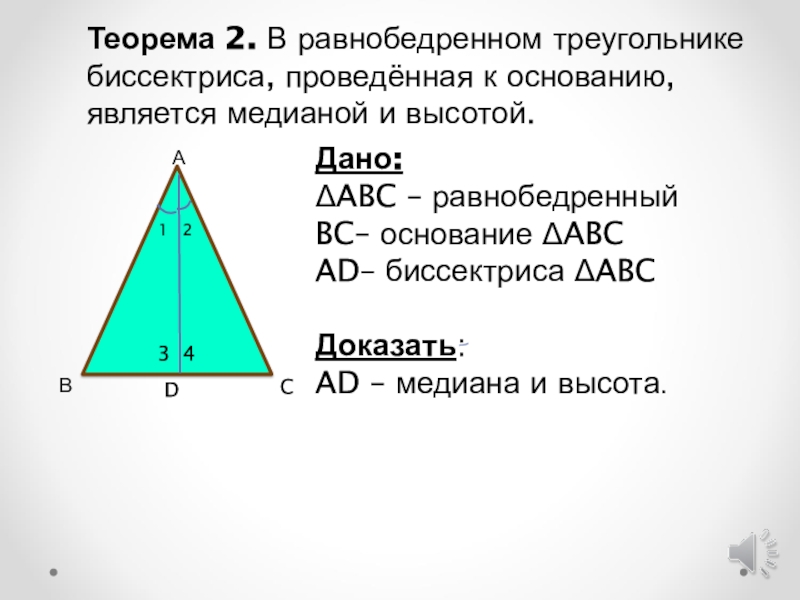
- 5. Дано:ΔABC – равнобедренныйBC– основание ΔABCAD– биссектриса ΔABCДоказать:
- 6. Доказательство:1) Рассмотрим ∆ABD и ∆ACD: Следовательно, ∆ABD=∆ACD (по первому признаку равенства треугольников). ВCD3 41 2А
- 7. 1. Медиана равнобедренного треугольника, проведённая к основанию,
- 8. Скачать презентанцию
Свойства равнобедренного треугольника BAC