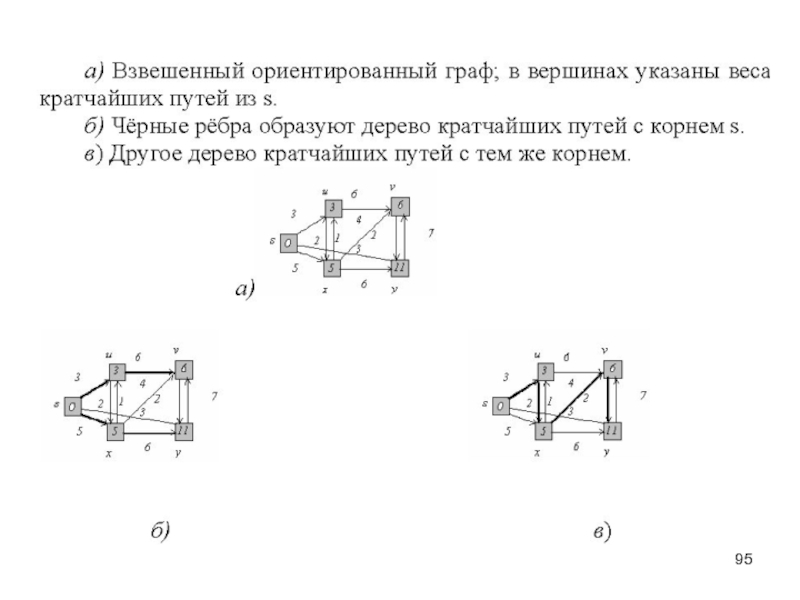
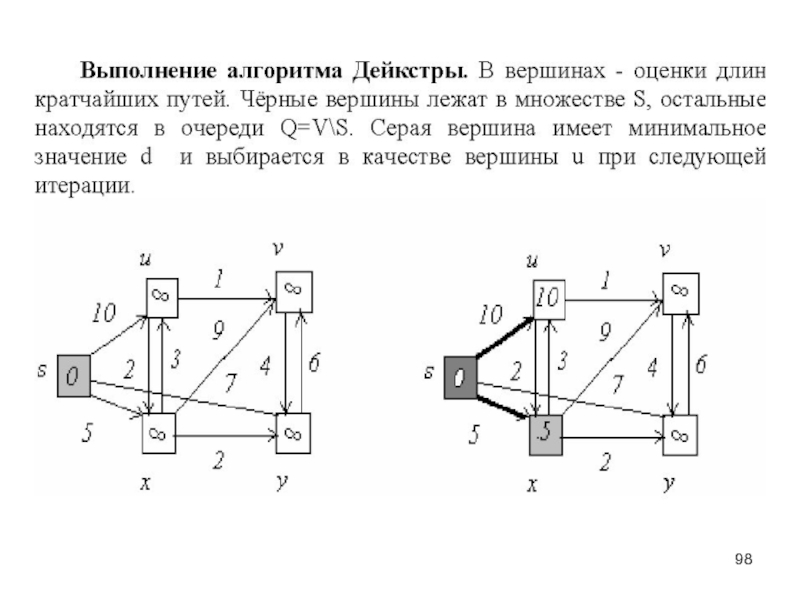
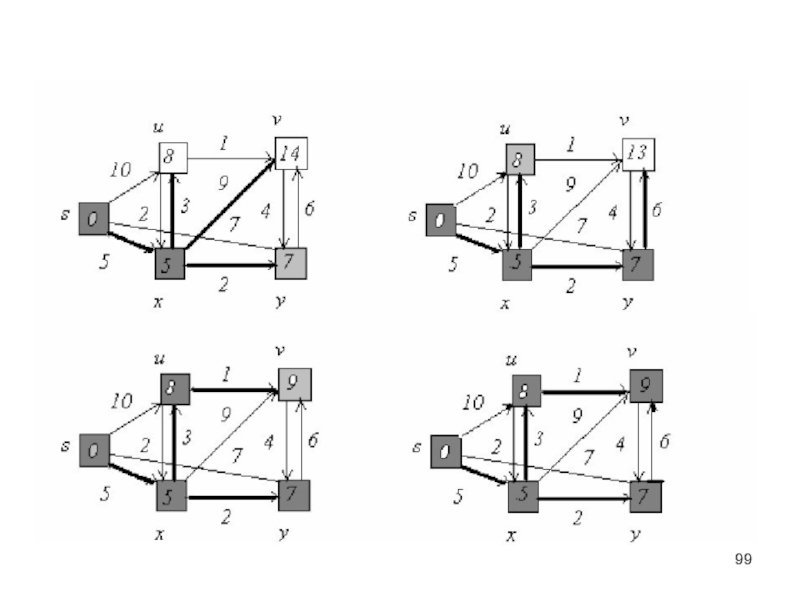
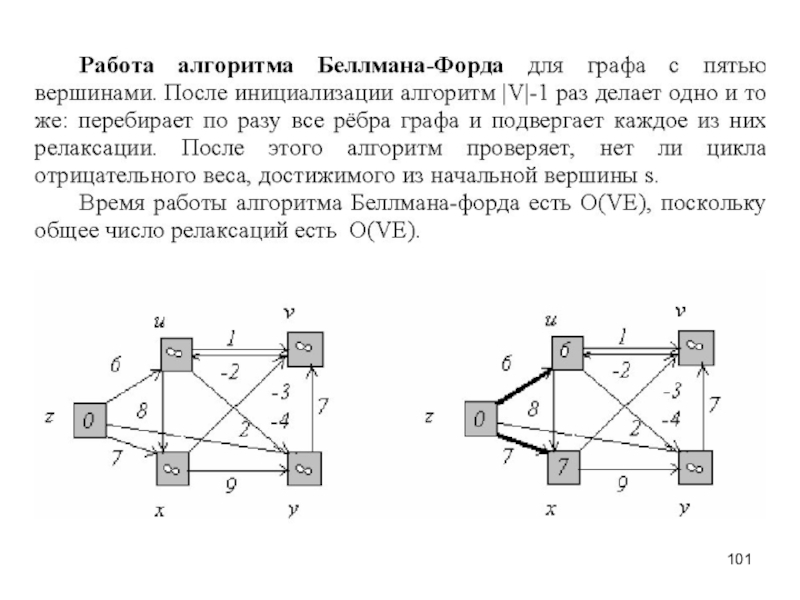
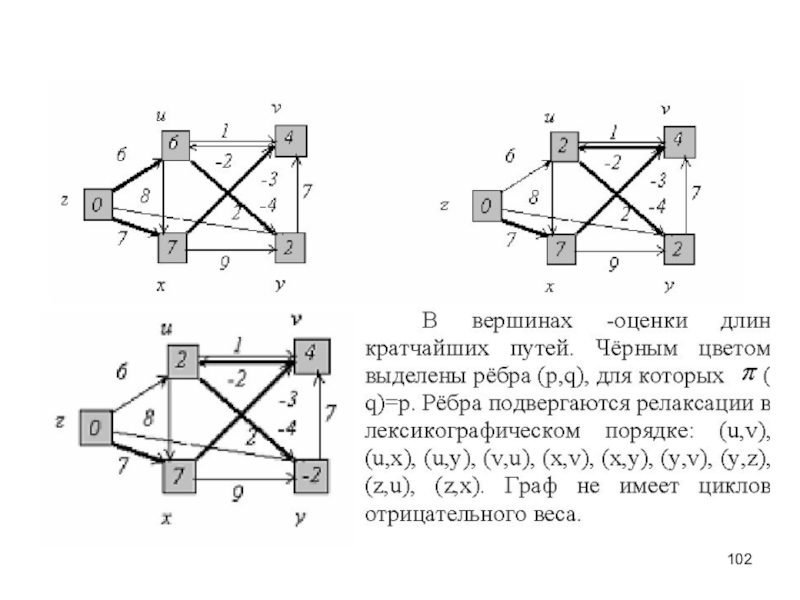
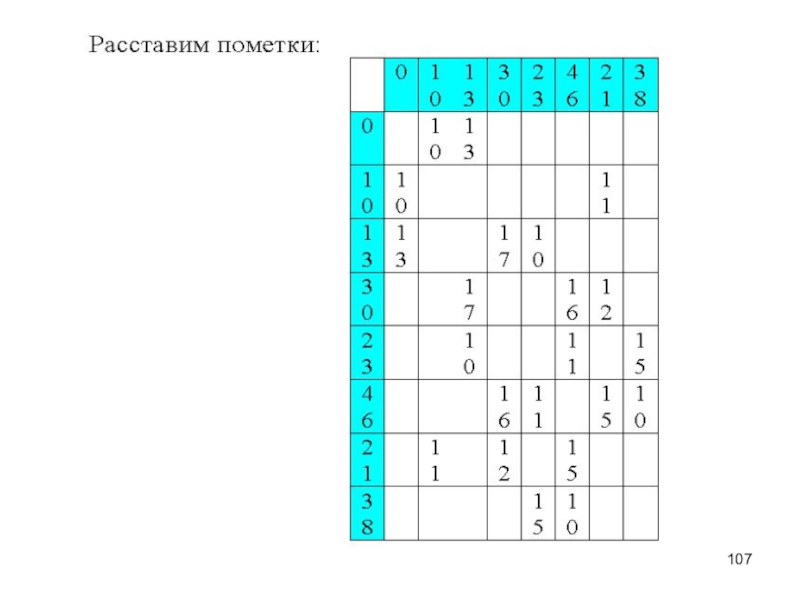
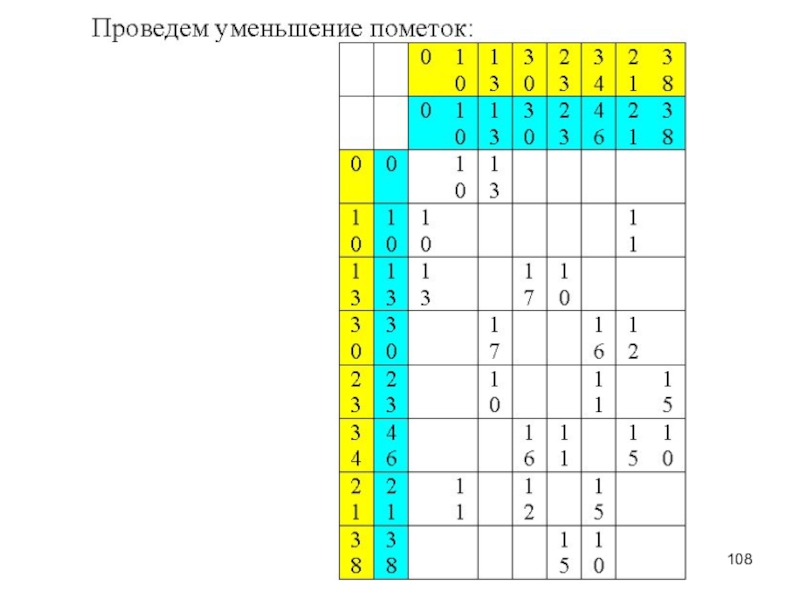
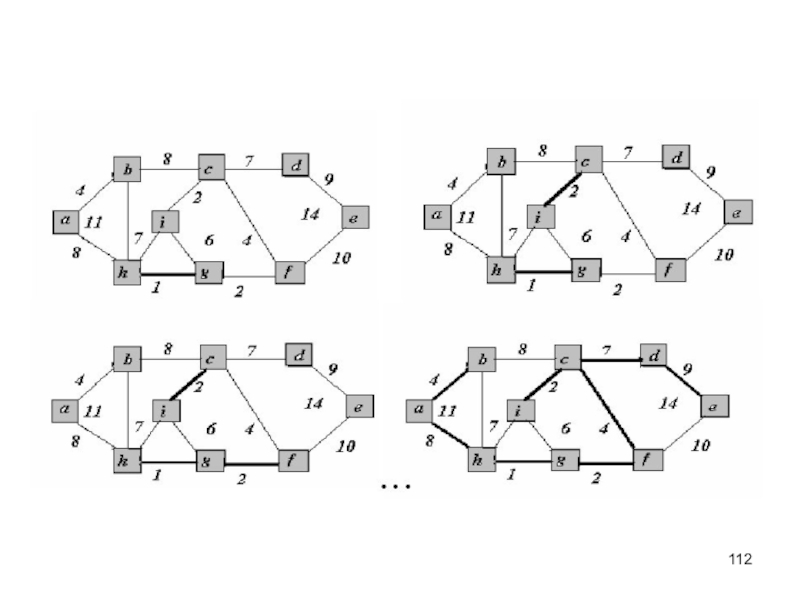
– определённая совокупность объектов. Объекты - элементы множества.
Примеры множеств
а) N
– мн-во натуральных чисел 1, 2, 3,…;б) P – мн-во всех простых чисел 2, 3, 5, 7…;
с) Z – мн-во всех целых чисел …-2, -1, 0, 1, 2,…;
d) R – мн-во всех действительных чисел.
- x принадлежит М. - x не принадлежит М.
Мн-во, элементы которого мн-ва, называются классом или семейством.
Мн-во, не содержащее элементов, называется пустым – ø.
Универсум (U) – достаточно широкое мн-во, из которого берутся элементы в каждом конкретном случае.
Способы задания мн-в: 1) перечисление элементов: ;
2) порождающей процедурой, например
3) характеристическим предикатом, например .






![Раздел 1. Множества, отношения и алгебраические структуры Теорема Кантора Т. Мн-во всех действительных чисел отрезка [0,1] не является Теорема Кантора Т. Мн-во всех действительных чисел отрезка [0,1] не является счётным. Док-во. (от](/img/thumbs/bb5ce9939ce41df6f4620a80a50d340d-800x.jpg)