все числа
из промежутков (−∞; −3) и
(2; + ∞)
Ответ:
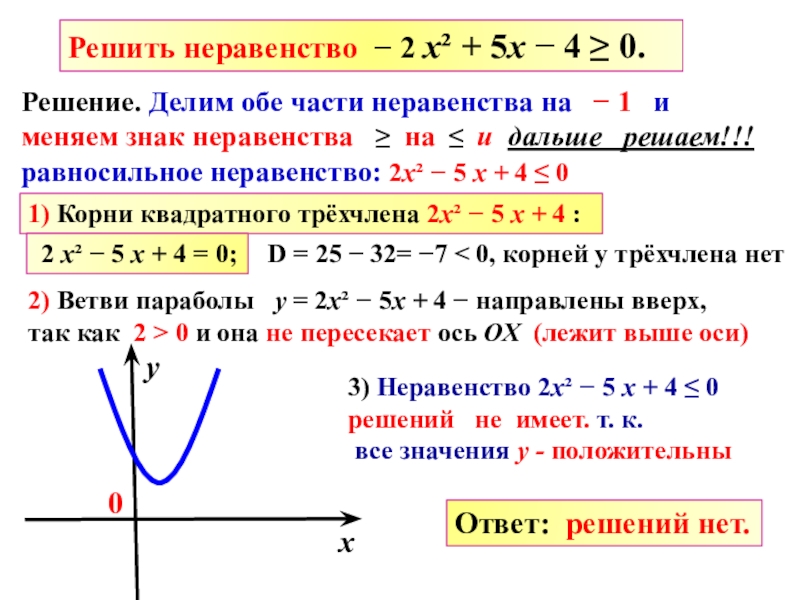
(−∞; −3); (2; + ∞)Решить неравенство − 2 х² − 2 х + 12 < 0.
Решение. Делим обе части неравенства на −2 и
меняем знак неравенства < на > и дальше решаем!!!
равносильное неравенство: х² + х − 6 > 0
///////
○
○
D = 1 + 24 = 25
х 1 = 2, х 2 = – 3
2) Ветви параболы у = х² + х − 6 − направлены вверх,
так как 1 > 0
1) Корни квадратного трёхчлена х² + х − 6 :
х² + х − 6 = 0;