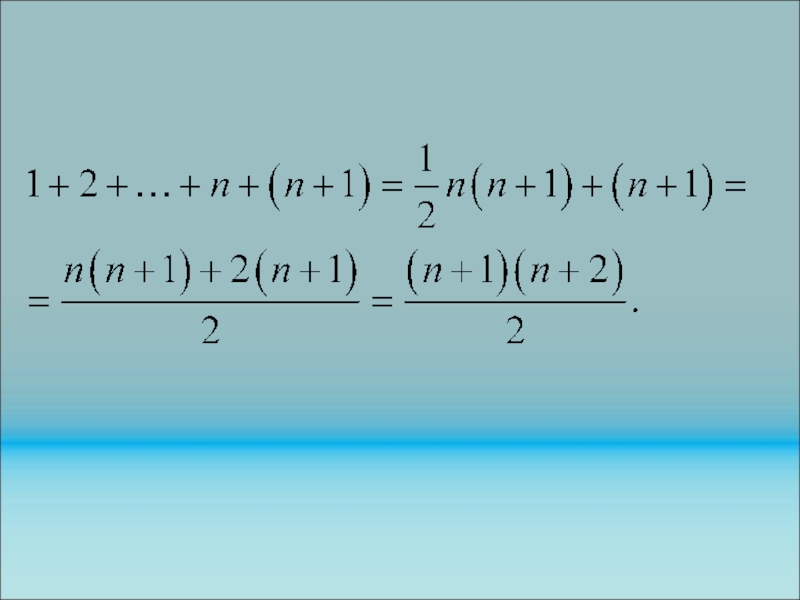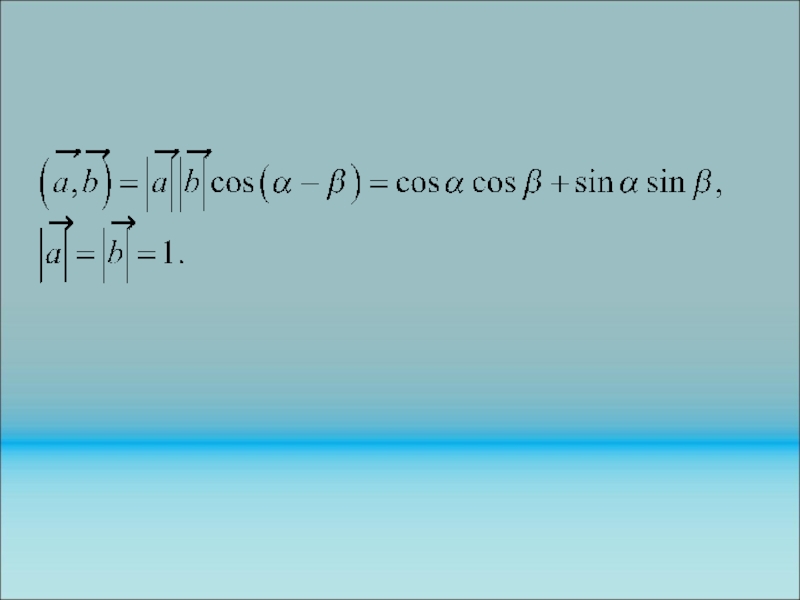Слайд 3МАТЕМАТИКА
Учебники:
1. Б.Ш.Гулиян, Р.Я.Хамидуллин
Математика . Базовый курс, М. ООО
«Маркет ДС Корпорейшн,2008.
Слайд 4Эпиграф
Истина нуждается в недосказанности.
Слайд 5ДОМАШНЕЕ ЗАДАНИЕ
А. В собственной тетради (для домашних работ) представить до
26 сентября с.г. решение Задания №1 из тетради-практимума.
Б.Студенческий билет(договор)
№_________
найти вторую цифру номера студенческого билета и приравнять ее, а =(если вторая цифра равна нулю, то а=3), b – третья цифра номера(если третья цифра равна нулю, то b=-5), c –четвертая цифра(если четвертая цифра равна нулю, то c=-1),
а =___, b =___, с =____
Слайд 6ДОМАШНЕЕ ЗАДАНИЕ (продолжение): решить систему
Найти сумму комплексных чисел:
Слайд 7ДОМАШНЕЕ ЗАДАНИЕ
Найти определитель
Слайд 8ТЕМЫ ВОЗМОЖНЫХ ПРЕЗЕНТАЦИЙ (необходимо предоставить до 1 декабря с.г.)
1. Метод
математической индукции
2. Комплексные числа
3. Тригонометрические функции
4. Решение квадратного уравнения. Теорема
Виета
5. Производная
6. Интеграл
Слайд 9ТЕМЫ ВОЗМОЖНЫХ ПРЕЗЕНТАЦИЙ (необходимо предоставить до 1 декабря с.г.)
1. Метод
математической индукции
2. Комплексные числа
3. Тригонометрические функции
4. Решение квадратного уравнения. Теорема
Виета
Слайд 10дидактические единицы
Основные дидактические единицы: числа, множество, последовательность, функция, график функции,
линейная зависимость, степенная функция, логарифм, тригонометрические функции, система уравнений, матрица,
определитель матрицы, предел, последовательность, непрерывность (функции), производная, интеграл.
Слайд 11Введение
Мы начинаем с алгебры. В устройстве мира топологические свойства лежат
на поверхности, алгебраические - в глубине. Поэтому алгебра несколько уступает,
хотя геометрия в школе - падчерица. В результате кое-что может не обнаруживаться – вплоть до законов мироздания. Сразу заметим, что математика -доброжелательная наука.
Слайд 12Предварительные общие сведения
В математике ценны «маневры» в общем смысле. Многие
разделы математики можно себе представить, как изучение множества (назовем его
А) объектов с определенным в этом множестве операциями. Об операциях будет сказано. Некоторые операции выполняются легко, а какие-то встречают трудности. Большую пользу может принести попытка установить взаимно-однозначное соответствие
Слайд 13Предварительные сведения
нашего множества А с каким-нибудь другим множеством
В, и посмотреть, какие операции в множестве В соответствуют операциям
в множестве А. Если действия в множестве В проще операций в А, то задачу можно решать следующим образом. Объекты из А трансформируются в В, там выполняются действия, и результат возвращается в А.
Слайд 15Алгебра. Введение. История
Предметом алгебры для нас является, в первую очередь,
изучение уравнений и функций, решение (систем) уравнений.
Истоки алгебры восходят к
глубокой древности, когда 4000 лет назад ученые древнего Вавилона (Шумера) решали квадратное уравнение.
В фундаменте алгебры лежит понятие числа. Мы привыкли к этому понятию, но это не означает простоты. Ему долго предшествовал примитивный счет
Слайд 16Алгебра. Введение
конкретных предметов.
В языке многих народов названия чисел в какой-то
степени совпадают с названиями пальцев рук. Например, в современном итальянском
языке слово «le dita» означает и «числа до десяти» и «пальцы». Надо помнить о том, что к привычному понятию числа, привычным цифрам 0, 1, 2, 3, 4, 5, и т.д. Человечество пришло в результате долгого исторического развития.
Слайд 17 АЛГЕБРА
Заметим, также, что применяемая нами в алгебре система
позиционная, когда цифра, в зависимости от места (позиции) в числе
имеет разное значение. Наша (индийская) система счисления – десятичная. У племени майя, например, двадцатеричная.
В любой позиционной системе операции осуществляются так же,
Слайд 18 АЛГЕБРА
как в десятичной, только учитывается, что переход
от одного разряда к другому осуществляется через степени основания системы.
У
древнегреческих математиков встречаются первые абстрактные обозначения для неизвестных величин. Например, Диофант именует неизвестную величину – «аритмос» и обозначает ее первыми буквами «ар».
Слайд 19 АЛГЕБРА
буквами «ар». Надо сказать, что до нас
дошли сочинения Диофанта, которые стали отправной точкой для теоретико-числовых исследований
П. Ферма, Л. Эйлера, К. Гаусса и других математиков.
Слайд 20Диофант, александрийский математик, ок. 325—409 г н.э.
Слайд 21Именем Диофанта названы два больших раздела теории чисел - теория
диофантовых уравнений и теория диофантовых приближений. Он оставил труды по
арифметике целых и дробных чисел и трактат о многоугольных числах. Им введен в математику неопределенный анализ и т.д. Ниже приведена страница его «Арифметики» (х3 8-х2 16= х3)
Слайд 22 ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ
Выражения, получающиеся из чисел и букв
с помощью арифметических операций и возведения в степень, называются алгебраическими.
Алгебраические
выражения подразделяются на рациональные и иррациональные. Например.
2х0,5 – иррациональный одночлен (выражение, функция)
Слайд 23Применяемые обозначения
Приведем основной принцип «наивной теории» множеств. Идея заключается в
том, что для любого свойства s(x), где встречается переменная х
существует совокупность множеств, обладающих этим свойством. Слова функция и отображение будут употребляться как синонимы.
Слайд 24Теоретические основания понятия числа
Термин «число» обычно понимается как натуральное, целое,
рациональное, вещественное, а в общем случае, комплексное число. Это понятие
неразрывно связано с операциями: сложением, вычитанием, умножением, делением, а также порядком, метрикой, топологией.
Слайд 25Теоретические основания понятия числа
Примечательно, что очень небольшое число важных математических
свойств – линейная упорядоченность, алгебраическая замкнутость определяет вещественные числа.
Обычно определения
числовых структур начинают с определения исходного множества - натуральных чисел.
Слайд 26Понятие натурального числа
Можно констатировать, что множество N фундаментально в математике.
Например, понятие пространства по современным представлением утратило свой независимый статус
и может быть сведено к понятию числа, т.е. в конечном счете к понятию натурального числа.
Слайд 27Существуют различные подходы в определении натурального числа. Рассмотрим два подхода,
которые можно распространить на другие математические объекты: финитный и теоретико-множественный.
При финитном подходе рассматривается два алфавита: { | } и {0, 1}. Натуральным числом называется любое непустое слово в первом алфавите или любое непустое слово во втором
Слайд 28 алфавите, не начинающееся с нуля. Например, { ||| }
означает число три. Два определения связывает между собой вычислимая функция.
Арифметические действия и функции очевидным образом определяются некоторыми программами (алгоритмами). Например,
Слайд 30
Рассматриваемое нами понимание натурального числа просто и наглядно.
Итак, финитная точка зрения (удобная для ЭВМ) состоит в определении
числа как слова и алгоритма. Однако она имеет недостатки.
Слайд 31Теоретико-множественный подход в определении натурального числа основан на рассмотрении математического
объекта как множества. Число нуль определяется как пустое множество. Число
один как множество, состоящее из одного элемента и т.д. Другими словами, натуральный ряд чисел – наименьший элемент в семействе предельных ординалов. Ординал – это множество, для которого задано определенное условие. Смысл – элементы множества – сами являются множествами.
Слайд 32Понятие целого числа
Целое число (множество Z)можно определить как упорядоченную пару
вида (s, n), где n - натуральное число, а s
множество, состоящее из двух знаков (+, -). Операции и отношение порядка (какое число больше) в множестве натуральных чисел индуцируют соответствующие операции в целых числах. Далее будем считать, что натуральные числа не содержат числа нуль.
Слайд 33Рациональные и вещественные числа
Считается, что рациональное число (Q)есть отношение целого
к натуральному.
Вещественные числа
Вещественные числа задаются пространством R1 –
линейным векторным одномерным вещественным пространством. Вещественные числа мы можем приближенно определить как
Слайд 34Вещественные числа. Комплексные числа
бесконечные десятичные (или двоичные) дроби.
Кроме вещественных чисел существуют и другие числа. Рассмотрим комплексные числа.
В развитии комплексных чисел особенно велика заслуга Леонарда Эйлера.
Слайд 35Понятие комплексного числа
Комплексные числа стали широко использоваться с 18 века.
Формально комплексное число задается в виде упорядоченной пары вещественных чисел
(х, у). Оно может быть также задано в виде матрицы, либо алгебраически в виде х+iy. Например, операции сложения (и вычитания) определяются покоординатным сложением (и вычитанием):
z1+ z2 =(x1+ x2)+i(y1+ y2)
Слайд 36Понятие комплексного числа
Например, z1=2+i3, z2=4-i,
z1+ z2 =(2+4)+i(3-1)=6+i2
Следует особо отметить умножение
упорядоченной пары вида (0,1) на саму себя (0,1)∙(0,1).
Слайд 37Понятие комплексного числа
Оно равно числу (-1,0), что кратко записывается i2
=-1. В конечном итоге достигается алгебраическое расширение поля вещественных чисел.
Комплексные числа полезны во многих отношениях. Если, например, в теории линейных дифференциальных уравнений ограничиться вещественным случаем, то красивая теория превратится в клубок загадочных фактов и т.д.
Слайд 38Понятие комплексного числа
Комплексным числам соответствуют определенные матрицы. Единице соответствует
Свойства квадрата
i2 =-1 легко проверяются, если использовать классическое умножение матриц.
Слайд 39Понятие комплексного числа
Умножение комплексных чисел проводится по правилу раскрытия скобок:(х1+iу1)(х2+iу2)=х1х2+ix1y2+iх2у1+iy1iу2
= х1х2+i(x1y2+х2у1)-y1у2 .
Слайд 40ПОНЯТИЕ ЧИСЛА
Алгебраические числа Трансцендентные числа
Рациональные
Целые Дроби Алгебраические
Натуральные иррациональные
Алгебраическими называются числа,
являющиеся
корнями полиномов.
Слайд 41Трансцендентные числа
Трансцендентные числа (от латинского transcendere — превосходить, переходить) – иррациональные
числа, не являющиеся алгебраическими.
Пример. Основание натуральных логарифмов- число Непера е
(е =2,71…). Число Архимеда ( =3,14…).
Слайд 42Понятие функции
Забегая вперед рассмотрим понятие функции. Изучение окружающих явлений показывает,
что переменные величины изменяются не независимо друг от друга, а
изменение численных значений одних из них влечет за собой изменение значений других. Например, площадь круга есть функция его радиуса, и эта зависимость записывается формулой S = r2.
Слайд 43
Другими словами, функция (с 17 в.) может быть задана формулой, выражающей зависимую
переменную через одну или несколько независимых переменных.
Пусть дано множество
Х и если указан закон (правило), обозначаемый буквой f, по которому каждому значению величины х из множества Х ставится в соответствие одно вполне определенное значение величины y множества Y, то говорят, что на множестве Х задана функция вида .
Слайд 44При этом х называется независимой переменной (или аргументом), у
— зависимой переменной или функцией.
Множество Х называют областью определения (или
существования) функции и обозначают D, а множество Y обозначают E и называют областью значений функции.
Слайд 46Далее мы определим понятие наибольшего общего делителя чисел, а затем
определим метод математической индукции. Наибольшим общим делителем (НОД) для двух
целых чисел m и n ( иногда обозначается (m, n)) называется наибольший из их общих делителей. Пример: для чисел 70 и 105 наибольший общий делитель равен 35, для чисел 126 и 2310 наибольший общий делитель равен 42.
Наибольший общий делитель существует и однозначно определён, если хотя бы одно из
Слайд 47чисел m или n не ноль. Все общие делители этих
чисел являются делителями НОД. Для определения наибольшего общего делителя двух
чисел сначала делят большее на меньшее, а затем меньшее на остаток, и далее первый остаток на второй и т.д. Наименьшим общим кратным (НОК) двух целых чисел m и n называется наименьшее натуральное число, которое делится на m и n.
Наибольший общий делитель и наименьшее общее кратное связаны соотношением:
НОД(m,n) НОК(m,n)=mn
Слайд 48С НОД(m,n) и НОК(m,n) связана интересная алгебраическая структура, когда на
множестве чисел, делителей некоторого числа, вводятся операции типа х+у
= НОД(х,у) и ху=НОК(х,у). Такая структура (алгебра) применяется в теории чисел.
Если многочлены связаны соотношением
Q(x)=U(x)V(x)
то U и V считаются делителями Q. Наибольшим общим делителем (НОД) называется такой делитель, который делится на все другие общие делители.
Слайд 49В математике широкое применение находит метод или принцип математической индукции.
Строгое его обоснование проводится в теории множеств. Пусть имеется некоторое
выражение А(n), зависящее от натурального n. Если на первом шаге мы доказываем истинность А(1) (базис индукции) и, если (на втором шаге) из истинности А(n) следует истинность А(n+1), то А(n) истинно для всех n.
Слайд 50 Пример. Доказать, что для любого натурального числа справедливо
равенство:
Проверяем равенство для n=1. Получаем 1=1.
На втором шаге предполагаем истинность
(1) для n.
3. Необходимо доказать истинность нашего выражения для случая n+1.
Слайд 52 Мы доказали, что для случая n+1 наше равенство
(1) истинно, т.е. оно истинно всегда, для любого n.
Рассмотрим понятие алгебраической структуры.
Операцией или внутренней операцией на множестве М называется отображение
М М М, т.е. закон, по которому каждой упорядоченной паре элементов из М ставится в соответствие единственный элемент из М.
Пример. Для множества вещественных или
Слайд 53 комплексных чисел такой операцией является умножение и сложение.
Говорят, что на множестве М задана алгебраическая структура, если
на нем определены одна или несколько внутренних операций (и внешних), которые удовлетворяют условиям (обычно это ассоциативные, коммутативные и дистрибутивные операции).
В зависимости от наличия внутренних (и внешних) операций выделяют
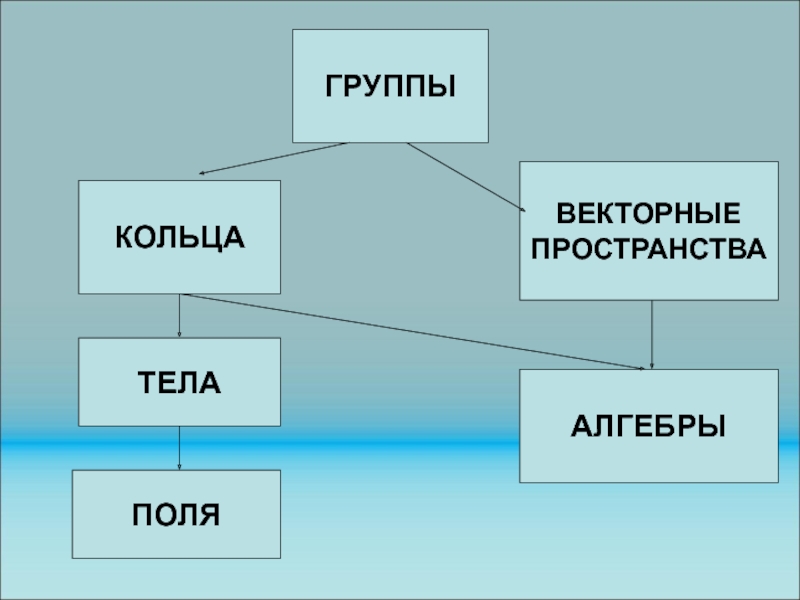
Слайд 54 различные алгебраические структуры. Наиболее важными из них
являются группы (одна внутренняя операция, которая называется «сложение» или «умножение»,
например, группа подстановок), кольца (две внутренние операции «сложение и умножение»), векторные пространства (одна внутренняя операция – сложение векторов и одна внешняя операция – умножение вектора на число) и алгебры (две внутренние операции -
Слайд 55 «сложение и умножение» - и одна внешняя операция
– умножение элементов этого множества на число). Важным типом колец
являются тела (кольца с единицей, в которых каждый отличный от нуля элемент имеет обратный). Коммутативное тело называется полем.
Примеры. Кольцом является множество квадратных матриц. Полями являются множество рациональных чисел, а также множество вещественных и комплексных чисел.
Слайд 56ГРУППЫ
КОЛЬЦА
ТЕЛА
ПОЛЯ
ВЕКТОРНЫЕ
ПРОСТРАНСТВА
АЛГЕБРЫ
Слайд 57Линейной функцией одного переменного называют функцию вида у=ах+b. В высшей
математике ее называют аффинно-линейной функцией аргумента х. Число а называется
угловым коэффициентом. Строгое определение линейной функции таково: линейной функцией называется любой гомоморфизм группы R+ в себя, т.е. функция, обладающая свойством
f(х+у)=f(х)+f(у).
При этом считается, что функция f непрерывна.
Слайд 58Свойства линейной функции у=ах.
Функция нечетна
Следующее свойство связано с операцией умножения.
Оно несколько неожиданно, т.к. в самом определении функции ничего не
говорится об умножении.
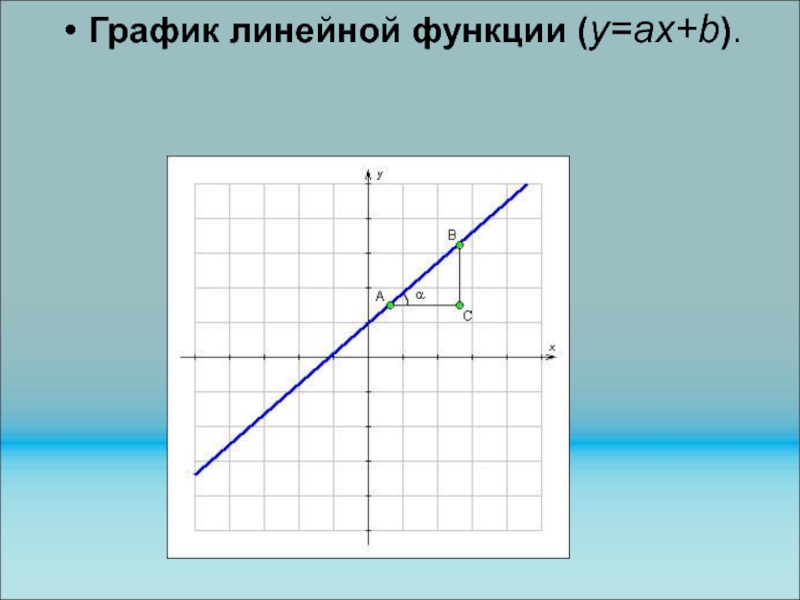
Слайд 59График линейной функции (у=ах+b).
Слайд 60Линейная функция
Число b равно ординате точки пересечения графика функции у=ах+b
с осью Оу.
Угловой коэффициент равен тангенсу угла наклона графика (угла
).
Если b=0, то график функции проходит через начало координат.
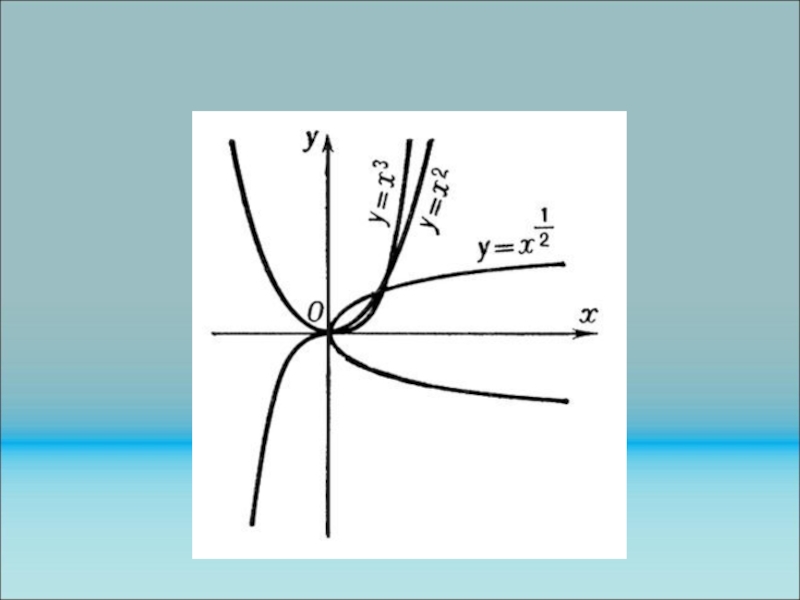
Слайд 61По аналогии с линейной функцией определяем степенную функцию хn .
Степенной функцией называется непрерывный гомоморфизм группы R>0 в себя, т.е.
функция, обладающая свойством
f(ху)=f(х) f(у).
При этом считается, что функция f непрерывна.
Определение степенной функции содержит важный момент: оно иллюстрирует «двойственность»
Слайд 62 между функциями и их аргументами. Если мы фиксируем
некоторое значение аргумента х и каждой функции f, определенной в
точке х, из множества всех функций поставим в соответствие значение этой функции – число f(х). Тем самым число х определяет функцию f(х), заданную на множестве функций. Другими словами, аргумент и функция поменялись местами.
Встает вопрос о доопределении степенной функции. Можно ли продолжить функцию хк, где k равно 1/n на всю числовую прямую? Имеется в виду функция – обратная к хn.
Слайд 63Получаем, что при нечетном n функция хn – инъективна, т.е.
Однако при четном n функция хn – не инъективна. Например,
при n =2 функция
не определена на множестве действительных чисел.
Слайд 64Довольно сложно доказать существование и единственность степенной функции (мы не
будем это делать). Приведем основные свойства:
Слайд 65
5. Функция ха монотонно возрастает при a>0 и монотонно убывает
при a < 0.
6. Функция ха является изоморфизмом группы R>0
в себя тогда и только тогда, когда a не равно 0.
Слайд 66Примеры степенных функций
Квадратичная парабола х2
Слайд 67
Свойства квадратичной параболы. Область определения D=(-, ). Функция х2 четная
(симметрична относительно оси Оу. Абсцисса вершины параболы в общем случае
определяется по равенству
хв = -b/2a.
Слайд 68На рисунке представлены основные алгебраические функции
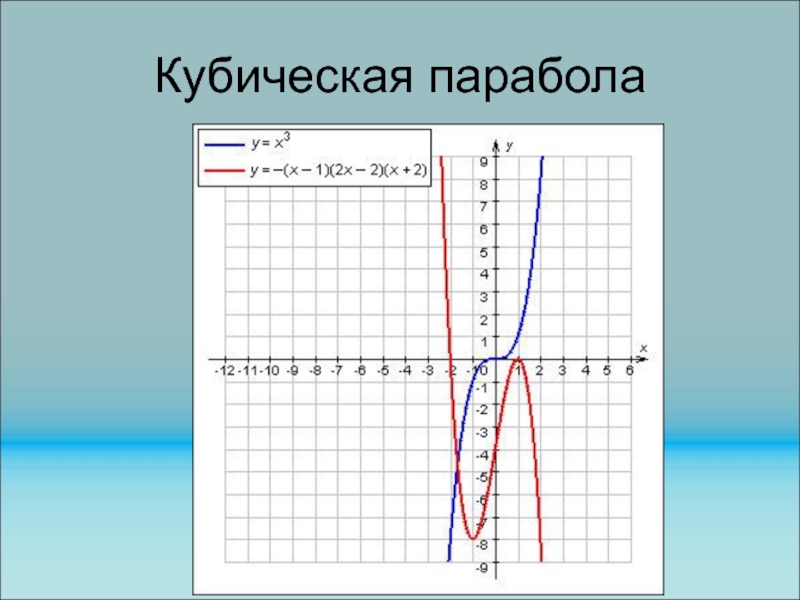
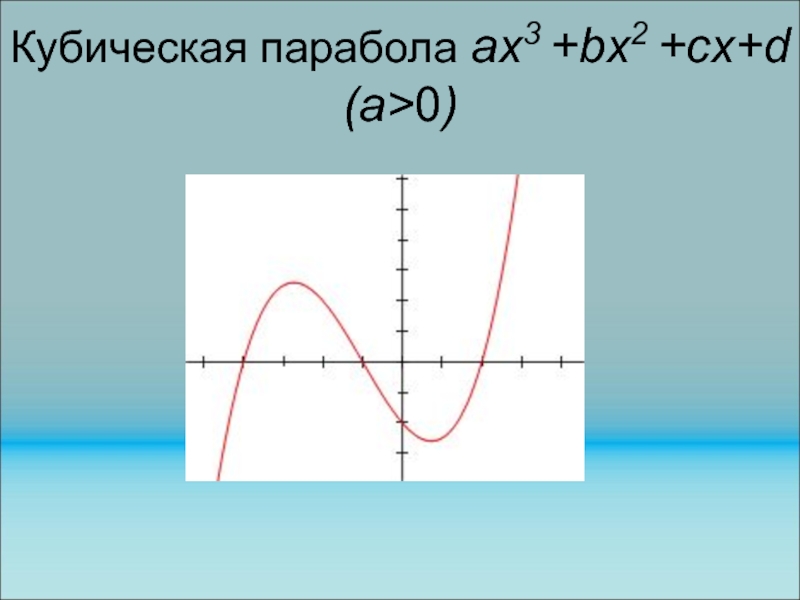
Слайд 70Кубическая парабола ах3 +bх2 +cх+d (а>0)
Слайд 71ГИПЕРБОЛА
Термин «гипербола» (греч. ὑπερβολή — избыток) был введён Аполлонием Пергским (ок.
262 г. до н.э. — ок. 190 г. до н.э.
) поскольку задача о построении точки гиперболы сводится к задаче о приложении с избытком.
Слайд 72Гипербола
Подобно параболе, гипербола является незамкнутой кривой, т.е. неограниченно простирающейся в
бесконечность и не замыкающаяся на себя подобно эллипсу. Гипербола состоит
из двух отдельных кривых, которые называют ветвями. Ближайшие друг к другу точки двух ветвей гиперболы называются вершинами. Кратчайшее расстояние между двумя ветвями гиперболы называется большой осью гиперболы. Гипербола обладает зеркальной симметрией относительно действительной и мнимой осей, а также вращательной симметрией при повороте на угол 180° вокруг центра гиперболы.
Слайд 73Гипербола
На большом расстоянии от центра гипербола неограниченно приближается
к двум прямым линиям, которые называются асимптотами гиперболы. Асимптоты пересекаются
в центре гиперболы. Чем дальше расстояние от центра, тем ближе гипербола приближается к своим асимптотам, но никогда не пересекает их. Наклоны двух асимптот равны, но имеют противоположные знаки.
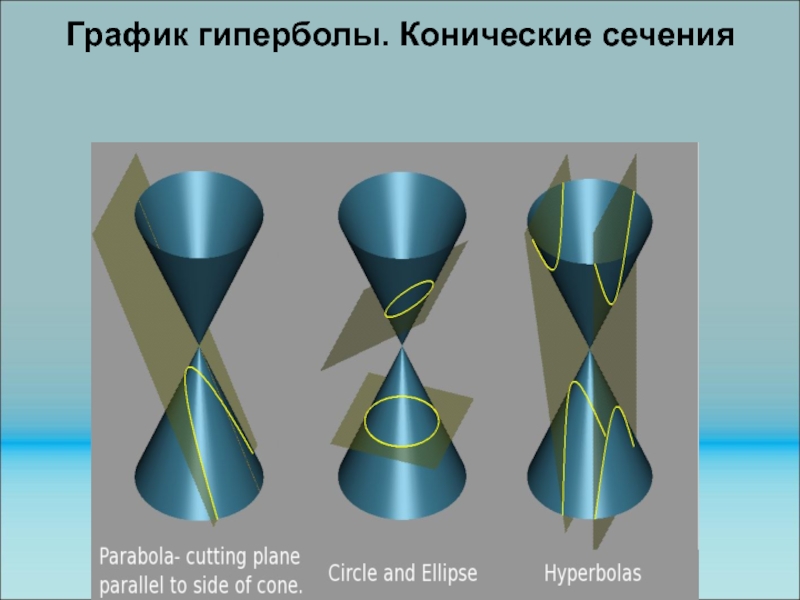
Слайд 74График гиперболы. Конические сечения
Слайд 75 Замечание. В зависимости от угла, плоскость пересекает коническую
поверхность по эллипсу, параболе или гиперболе (см. ниже).
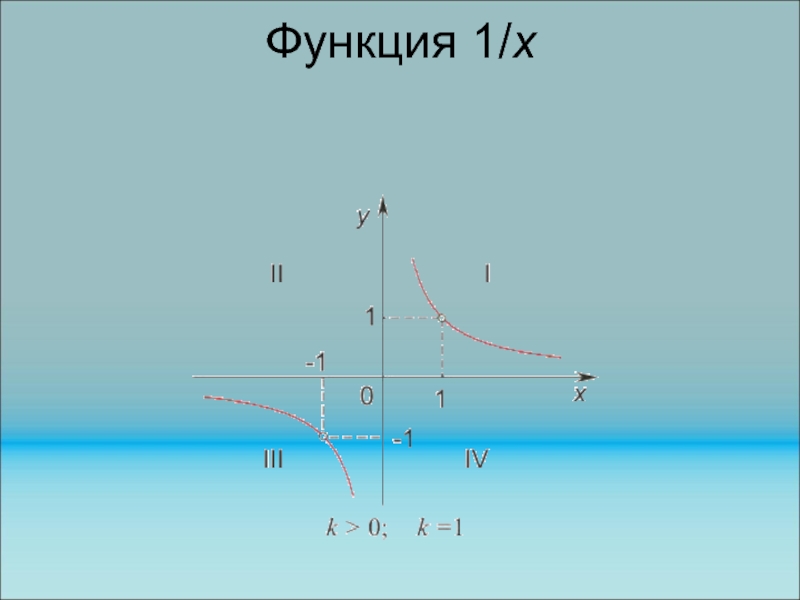
Слайд 76Гипербола. Функция k/x
В школе изучалась обратная пропорциональная зависимость
между величинами х и у, задаваемая соотношением
Слайд 79Функция 1/x (k/x)
Свойства гиперболы. Область определения D=(-, 0) (0,
). Точка О(0, 0) является центром гиперболы. Ось Оу называется
вертикальной асимптотой. К ней неограниченно приближается график функции, при значениях аргумента х неограниченно приближающихся к нулю. Ось Ох называется горизонтальной асимптотой. К этой прямой приближается график функции, при х стремящемся к бесконечности х .
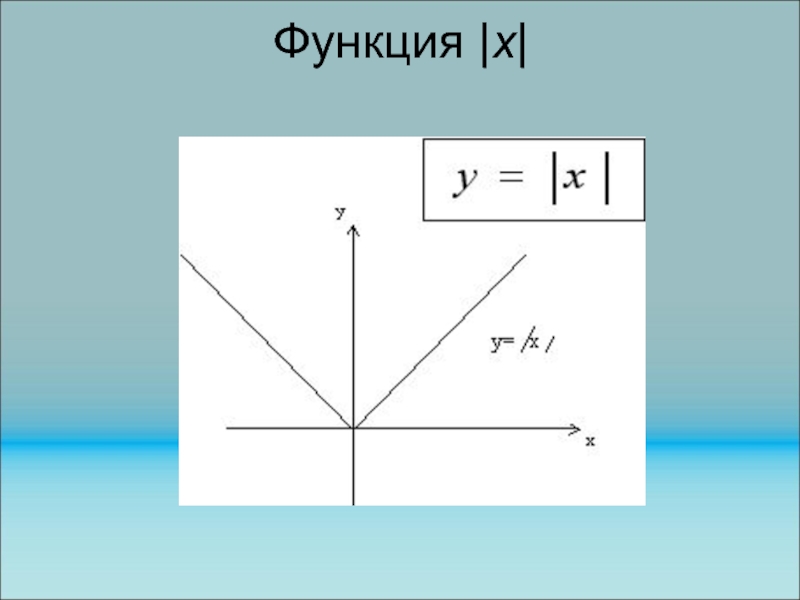
Слайд 80Функция |x|
Абсолютная величина числа х равна самому этому
числу, если х>0, равна противоположному числу, если х
равна нулю, если х=0. Функция модуль х является биссектрисой первого и биссектрисой второго координатных углов.
Слайд 82Взаимное расположение графиков прямой и обратной функций
Графики прямой
и обратной функций симметричны относительно биссектрисы первого и третьего координатных
углов.
Пример. Функции у=x2 и у= .
Слайд 84Исследование функций
При исследовании функции необходимо ответить на следующие
вопросы:
Какова область существования D?
Какова область изменения Е?
Ограничена
ли исследуемая функция?
Периодическая ли она?
Является ли функция четной/нечетной?
Слайд 85Исследование функций
Есть ли у нее точки пересечения
с осями координат?
Есть ли у нее промежутки монотонности?
Есть
ли у нее экстремумы?
Какой график исследуемой функции?
Слайд 86График функции
Графический способ задания позволяет увидеть функцию сразу (иногда целиком)
и наглядно представить ее свойства.
Функцию, как известно, часто задают с
помощью формул. Такой способ задания называется аналитическим. Если функция задана с помощью формул, но ее область определения не указана, то ее необходимо найти и областью определения считается множество всех х, при которых формула имеет смысл (!).
Слайд 87Уравнения
Уравнение – это равенство, содержащее одну или несколько неизвестных.
В общем виде записывается так f(x) = g(x),
или
F(x) =0, где F = f - g.
Например, линейное уравнение 1-й степени с одним неизвестным (линейная функция равна нулю)
ах+b=0.
Решить уравнение – значит найти все его корни или доказать, что корней нет.
Слайд 88Уравнения
Постараемся прежде всего ответить
на два вопроса. По какой причине могут потеряться корни уравнений? Для чего нужна проверка?
Прежде чем ответить на первый вопрос заметим, что очень часто при решении мы применяем к уравнениям некоторые преобразования. Получается, что источник потери корней (появления посторонних) – преобразования.
Слайд 89ОПРЕДЕЛЕНИЯ
1. Областью допустимых значений (о.д.з.) уравнения называется множество всех значений
неизвестной переменной, при которых все функции, входящие в уравнение, имеют
смысл.
2. Решением или корнем уравнения называются те значения неизвестных, при подстановке которых в уравнение получается верное числовое равенство.
Слайд 90ОПРЕДЕЛЕНИЯ
ЗАМЕЧАНИЕ. Все решения уравнения должны входить в область допустимых значений
(о.д.з.).
3. Если все корни одного уравнения являются корнями
другого уравнения, то второе уравнение называется следствием первого.
4. Два уравнения называются равносильными или эквивалентными, если каждое из них является следствием другого.
Слайд 91Преобразования уравнений
При преобразованиях и замене уравнений новыми происходит следующее:
1.
если новое уравнение не является следствием данного, то происходит потеря
корней (!);
2. если новое уравнение является следствием данного, но не равносильно ему, то появляются посторонние корни;
Слайд 92Преобразования уравнений
3. если новое уравнение равносильно данному, то их корни
совпадают.
ВЫВОД: если при решении уравнения применялись преобразования, приводящие к равносильным
уравнениям – проверка не нужна.
В качестве примера таких равносильных преобразований можно привести умножение (деление) обеих частей уравнения на одно и то же число,
Слайд 93
отличное от нуля или перенос любого числа с одной стороны
равенства на другую с изменение знака на противоположный (более подробно-ниже).
Если же решение уравнений проводилось без анализа равносильности получаемых уравнений – проверка является неотъемлемой частью решения.
Слайд 94 Правило замены.
Если заменить одну из функций (f(x)
или g(x)) на равносильную, то получим равносильное уравнение.
Правило подстановки.
Если А(х)=В(х)
(А и В равносильны), то заменив уравнение
f(x) = g(x) на f(x)+А(х) = g(x)+В(х) получим равносильное.
Рассмотрим возможные (основные) преобразования уравнений.
Слайд 95Преобразования уравнений
1. Преобразование первого вида – это взятие некоторой функции
от обеих частей уравнения (осторожно).
2. Ко второму типу относятся
тождественные преобразования внутри каждой части уравнения.
3. К третьему виду относятся умножение/деление обеих частей уравнения на некоторую функцию, отличную от нуля или прибавление
Слайд 96Преобразования уравнений
к обеим частям уравнения некоторой функции или
числа.
В результате всех этих преобразований уравнение меняется и необходимо
принимать меры, чтобы не допустить потери корней.
Замечание. Необходимо помнить, что в общем случае перенос, преобразование и приведение подобных могут привести к появлению посторонних корней.
Слайд 97Преобразования уравнений
ОПРЕДЕЛЕНИЕ. Если функции, входящие в уравнение являются
многочленами от неизвестных переменных, то уравнение называется алгебраическим. В общем
случае алгебраическое уравнение может содержать иррациональные функции.
Алгебраическое уравнение n–ой степени с одним переменным можно записать в каноническом виде:
а0хn + а1хn-1 +… + аn-1х+ аn=0. (а0 не равно нулю).
Слайд 98Многочлены или полиномы
Слева стоит многочлен, котороый может записываться формально:Qn=а0хn +
а1хn-1 +… + аn-1х+ аn (а0 не равно нулю). Сумма
и произведение многочленов определяются по обычным правилам, что в итоге приводит к тому, что множество многочленов образует кольцо.
Справедлива теорема Безу: Остаток r при делении Qn на (х-с) равен Qn(с).
В конечном итоге получаем.
Слайд 99Основная теорема алгебры
ТЕОРЕМА. Всякое алгебраическое уравнение ненулевой степени
имеет по крайней мере один корень – действительный, комплексный или
мнимый.
Утверждение. Алгебраическое уравнение степени выше четвертой в общем виде в радикалах неразрешимо.
Уравнение вида f1(x)=f2(x) называется в общем случае дробно-рациональным, если функции f1 и f2 - рациональные
Слайд 100 Рациональными называются функции (выражения), в которых над неизвестными
переменными производятся только действия сложения, вычитания и умножения.
Уравнение называется дробно-рациональным, если неизвестная переменная входит в знаменатель дроби, содержащейся в уравнении.
Слайд 101Уравнение 1-ой степени (линейное)
Определение. Уравнением 1-ой степени называется
уравнение, представимое в канонической форме в виде: ax+b=0.
Это уравнение имеет по крайней мере один корень – действительный.
Если а не равно нулю, то уравнение имеет единственный действительный корень
х1 =-b/a.
Если а=0 и b=0, то уравнение имеет бесчисленное множество корней (в общем
Слайд 102Уравнение 2-ой степени (квадратное)
случае – комплексных).
Если а=0 но b не
равно нулю, то уравнение не имеет корней
Определение. Уравнением
2-ой степени (квадратным) называется уравнение, представимое в канонической форме в виде:
ax2 +bх +с=0.
Далее мы будем рассматривать только действительные числа.
Слайд 103Уравнение 2-ой степени (квадратное)
Определение. Уравнением 2-ой степени (квадратным)
называется уравнение, представимое в канонической форме в виде:
ax2 +bх
+с=0.
Мы видим, что оно получается при равенстве нулю квадратного трехчлена. Далее мы будем рассматривать только действительные числа.
Число действительных корней зависит от знака дискриминанта D=b2 -4ac. Дискриминант переводится как «различающий».
Слайд 104Уравнение 2-ой степени (квадратное)
Если дискриминант больше нуля, то имеются
два действительных корня. Если дискриминант равен нулю, то имеются два
совпадающих (кратных) действительных корня. Если дискриминант меньше нуля, то действительных корней нет.
Первый способ решения квадратного уравнения.
Находим дискриминант уравнения
D= b2 - 4ac.
Слайд 105Первый способ решения квадратного ур-я
Корни равны
Слайд 106Первый способ решения квадратного уравнения
Примечание. Из формулы нахождения корней
квадратного уравнения следует: в случае рациональных коэффициентов квадратного трехчлена, его
корни будут рациональными, если только дискриминант является точным квадратом рационального числа.
Слайд 107Франсуа Виет (1540-1603)- выдающийся французский математик, один из основоположников алгебры
Слайд 108Родился в 1540 г. в Фонтене-ле-Конт французской провинции Пуату. Учился
сначала в местном францисканском монастыре, а затем — в университете Пуатье,
где получил степень бакалавра. С 19 лет занимался адвокатской практикой в родном городе. Издал «Математический Канон» — труд по тригонометрии. Переехал в Париж и вскоре перешёл на государственную службу.
Виет сделал блестящую карьеру и стал советником сначала короля Генриха III, а после его убийства —Генриха IV.
Слайд 109
В 1591 ввёл буквенные обозначения не только для
неизвестных величин, но и для коэффициентов уравнений; благодаря этому стало
впервые возможным выражение свойств уравнений и их корней общими формулами. Ему принадлежит установление единообразного приёма решения уравнений 2-й, 3-й и 4-й степеней. Среди открытий сам Виет особенно высоко ценил установление зависимости между корнями и коэффициентами уравнений (теорема Виета).
Слайд 110Второй способ решения квадратного уравнения
Второй способ основан на
обратной теореме Виета.
Если х1 и х2 – корни квадратного уравнения,
то сумма их равна х1+х2=-b/a, а произведение равно х1х2=с/a.
Для приведенного квадратного уравнения (старший коэффициент равен 1)
x2 +рх +q=0 (1)
формулы Виета принимают вид
Слайд 111Второй способ решения квадратного уравнения
х1+х2=-р, х1х2=q (2).
Отсюда следует,
что если а=1, и х1 и х2 – такие числа,
что для них выполняется условие (2), то эти числа х1 и х2 – являются корнями соответствующего квадратного уравнения (1).
Формулы (2) устанавливают связь между коэффициентами уравнения и корнями.
Слайд 112Неполное квадратное уравнение
Если один из коэффициентов уравнения
ax2 +bх +с=0, (a≠
0)
равен нулю, т.е. b=0 или с=0, то уравнение называется неполным.
Неполное
квадратное уравнение решается таким способом:
ax2 +bх=0, (a≠ 0, с=0)
х(ax +b)=0, x1 =0, х2 =-b/а.
Слайд 113Приводимость многочленов
Полином а0хn + а1хn-1 +… + аn-1х+ аn (а0
не равно нулю) называется приводимым, если он раскладывается в произведение
двух многочленов. Например, полином х2-1=(х-1) (х+1).
Существует несколько признаков неприводимости, которые используются для соответствующего доказательства.
Критерий Эйзенштейна.
Полином с целыми коэффициентами а0хn + а1хn-1 +… + аn-1х+ аn, удовлетворяющий
Слайд 114Приводимость многочленов
условию: все коэффициенты (кроме а0) делятся на
некоторое простое число р, но аn не делится на р2
, - неприводим (над полем рациональных чисел).
Например, многочлен хр-1 + хр-2 +… + х+1, где р – простое число, неприводим.
Существует интересный объект – производная многочлена. Она определяется формально. Производной полинома а0хn + а1хn-1 +… + аn-1х+ аn называется многочлен, равный nа0хn-1 +(n-1)а1хn-2 +… + аn-2х+ аn-1.
Слайд 115Производная многочлена
Мы видим, что это обычная производная степенной
функции (суммы). Но наше определение успешно работает и в общем
случае(!) многочлена над произвольным полем (т.е. когда производная не определена). При этом сохраняются свойства дифференцирования, вплоть до разложения в ряд Тейлора. Справедлива интересная теорема.
Теорема. Многочлен f=Р[х] над произвольным полем (!) имеет кратный корень х=с в том только случае, когда f(с)=f`(с)=0.
Слайд 116Системы уравнений
Рассмотренные ниже утверждения без труда переносятся на уравнения и
системы уравнений с произвольным числом переменных.
Уравнение с двумя
переменными x1 и х2 записывается в общем виде
f(x1 , х2)=g(x1 , х2),
где f и g – выражения с переменными x1 и х2.
Слайд 117Системы уравнений
Решением нашего уравнения является упорядоченная пара чисел (x10 ,
х20 ), при подстановке которых получаем верное равенство.
Наше
уравнение равносильно уравнению
f(x1 , х2) - g(x1 , х2)=0.
Поэтому можно считать, что уравнение с двумя переменными x1 и х2 имеет вид
F(x1 , х2) =0, где F = f - g.
Слайд 118Системы уравнений
Если дано несколько уравнений
f1 (x1 , х2)=g1 (x1
, х2),
f2(x1 , х2)=g2(x1 , х2),
…
fk(x1 , х2)=gk(x1 , х2),
то можно утверждать, что дана система уравнений.
Слайд 119Системы уравнений
Решением системы уравнений является упорядоченная пара чисел (x10
, х20 ), являющаяся решением каждого из уравнений, входящих в
эту систему.
ПРАВИЛО ЗАМЕНЫ.
Заменив в системе одно из уравнений на равносильное, получим систему, равносильную данной.
Слайд 120Системы уравнений
ПРАВИЛО ПОДСТАНОВКИ.
Если одно из уравнений системы
имеет вид
x=A,
где А - произвольное выражение, не содержащее
x, то, заменив во всех остальных уравнениях переменную x на А, получим систему, равносильную данной.
Слайд 121Система линейных уравнений
Рассматриваются обычно случаи, когда число неизвестных равно числу
уравнений.
Каноническая система двух линейных уравнений с двумя неизвестными имеет вид:
a11x1
+a12х2=b1
a21x1 +a22х2=b2
Система называется однородной, если все bi=0.
Слайд 122Система линейных уравнений
Для развития теории решения систем линейных уравнений нам
необходимо изучить дополнительный материал.
Итак…
Слайд 123Решению систем линейных уравнений со многими неизвестными посвящена математическая теория
- линейная алгебра. По сути - это теория линейных алгебраических
структур (линейных пространств, линейных отображений и т.д.). Но главным для нас является решение систем уравнений. В настоящее время линейные математические модели приобрели важную роль в большинстве естественных и экономических наук.
Слайд 124Решение системы линейных уравнений
со многими неизвестными
Слайд 125Рассмотрим понятие линейности. Линейность представляет весьма общее понятие. Все линейные
модели, процессы и явления обладают свойствами аддитивности и однородности. Аддитивность
в математическом смысле означает следующее: если действие х приводит к эффекту , а действие у приводит к эффекту , то совместное действие х+у приводит к эффекту + .
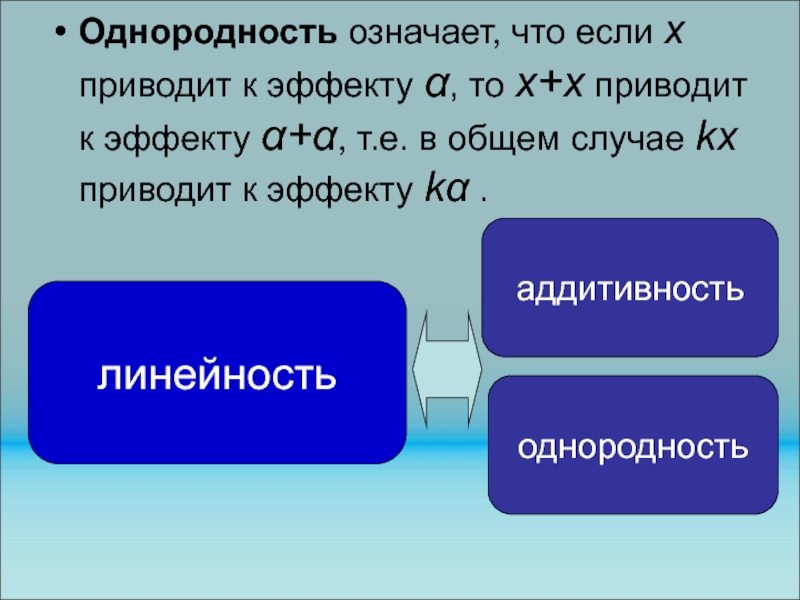
Слайд 126Однородность означает, что если х приводит к эффекту , то
х+х приводит к эффекту +, т.е. в общем случае kx
приводит к эффекту k .
линейность
аддитивность
однородность
Слайд 127С математической точки зрения линейные модели имеют определенные преимущества, т.к.
линейные задачи всегда решаются (в том смысле, что не может
сложиться ситуация, когда не известно имеет ли решение задача).
Еще в 4 в. до н.э. Тамарид решал систему уравнений. В Европе Баше де Мезирак [1587-1638] предложил решение в целых числах системы с двумя уравнениями.
Почти все линейные модели сводятся к системам алгебраических линейных уравнений или неравенств.
Слайд 128Леонтьевская модель
В начале 30-х годов прошлого века нобелевский лауреат В.
Леонтьев предложил линейную модель национальной экономики. Эта модель предполагает, что
экономика состоит из некоторого числа взаимодействующих отраслей, каждая из которых производит один вид продукции и использует один процесс производства.
Слайд 129Векторные пространства
Векторное (линейное) пространство – это множество объектов (называемых, естественно,
векторами), на котором задана операция сложения и умножения вектора на
скаляр (т.е. число).
Пример. Множество упорядоченных троек образуют векторное пространство при очевидном определении операций (наборы складываются покомпонентно). Оно часто называется арифметическим.
Слайд 130Векторное подпространство
Подпространство векторного пространства – это подмножество векторов, которое само
является векторным пространством.
Пример. Подпространство трехмерных векторов составляют вектора с последней
компонентой равной нулю (т.е. двумерные вектора).
Пересечение двух подпространств есть снова подпространство.
Слайд 131Линейная оболочка
Если S - подмножество векторного пространства V, то его
линейной оболочкой называется множество SpanS={a1·v1 + +…+ak·vk : ak
- скаляры, vk – элементы S}.
Заметим, что SpanS – всегда векторное пространство, даже если S не является векторным подпространством. Говорят, что S порождает векторное пространство V, если SpanS=V.
Слайд 132Векторы
Векторы часто используются в естественно-научных дисциплинах. В школе вектор определяли
как величину, характеризующуюся двумя важными свойствами – модулем (длиной) и
направлением. Геометрически его изображают отрезком со стрелкой (или жирной буквой). Модуль вектора обозначают в вертикальных отрезках |a|. Вектор свободен и его величина не зависит от местонахождения начальной точки, а только от модуля и направления. Мы будем
Слайд 133Векторы
этого условия. Существуют связанные и скользящие векторы.
Равенство векторов вводится следующим
образом.
Слайд 134Равенство векторов. Два вектора называются равными, если они совмещаются параллельным
переносом.
Слайд 135Векторы
Вектор можно представить как упорядоченную тройку (для трехмерного пространства) чисел
вида (х1; х2; х3). Векторы иногда записываются в фигурных скобках.
Модуль вектора по определению равен (обобщенная теорема Пифагора)
Числа х1, х2, х3 называются компонентами или координатами вектора.
Слайд 136Векторы
На множеств векторов вводится операция сложения и умножения на скаляр
(т.е. векторное пространство), которые определяются так:
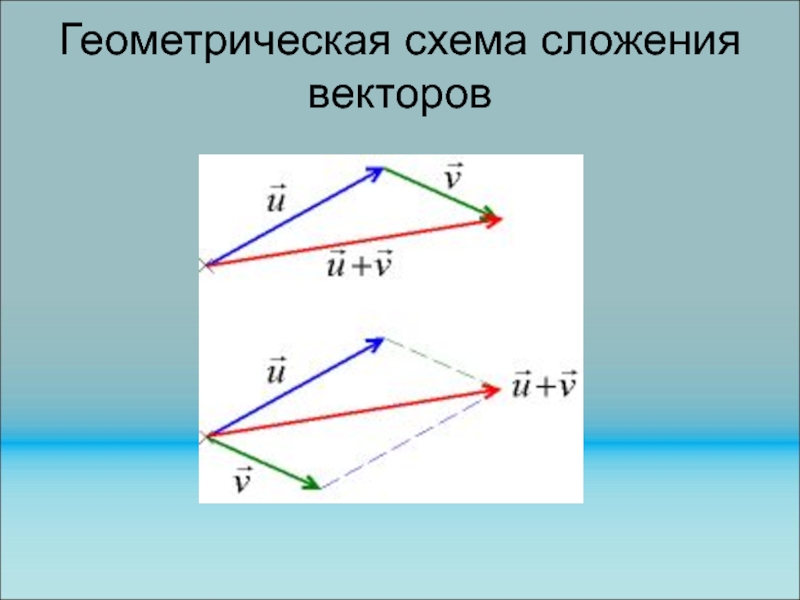
Слайд 137Геометрическая схема сложения векторов
Слайд 138Векторы
В пространстве (арифметическом линейном) имеется так называемый естественный или стандартный
базис (о базисе ниже) из трех (единичных) векторов
В этом
случае вектор
Слайд 139Векторы
представим в виде
Эти две записи можно рассматривать как эквивалентные.
Говорят, что вектор х разложим по векторам еi. Разложение вектора
по базису единственно. Концепция разложения векторов на составляющие весьма полезна.
Слайд 140Векторы
Если имеет место равенство
а = k1a1
+ k2a2 + k3a3,
то говорят также, что вектор
а является линейной комбинацией векторов a1, a2, a3.
Пространство, в котором размещаются вектора имеет размерность.
Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов. Размерность равна числу векторов базиса.
Слайд 141Линейная зависимость векторов
Множество векторов {an} называется линейно зависимым,
если существуют коэффициенты {kn} не все равные нулю, что
линейная комбинация равна нулю
k1a1 + k2a2 + k3a3=0.
Другими словами, если линейная комбинация равна нулю, но хотя бы один коэффициент отличен от нуля, то вектора линейно зависимы. В более общем случае, величины одного типа линейно независимы, если они
Слайд 142Линейная зависимость векторов
не удовлетворяют никакому линейному уравнению с
отличными от нуля скалярными коэффициентами.
Если векторы линейно зависимы, то
по крайней мере один из них линейно выражается через остальные. Подмножество векторов, не являющееся линейно зависимым, называется линейно независимым. Любое подмножество линейно независимого множества также линейно независимо.
Слайд 143Пример линейно зависимых векторов
Пример. Вектора на плоскости (-1; 4)
и (2; -8) линейно зависимы, т.к. их линейная (одна из
многих) комбинация равна нулю:
-2(-1; 4)-(2; -8)=0.
Здесь (хотя бы один) первый коэффициент (-2) отличен от нуля.
Слайд 144Пример
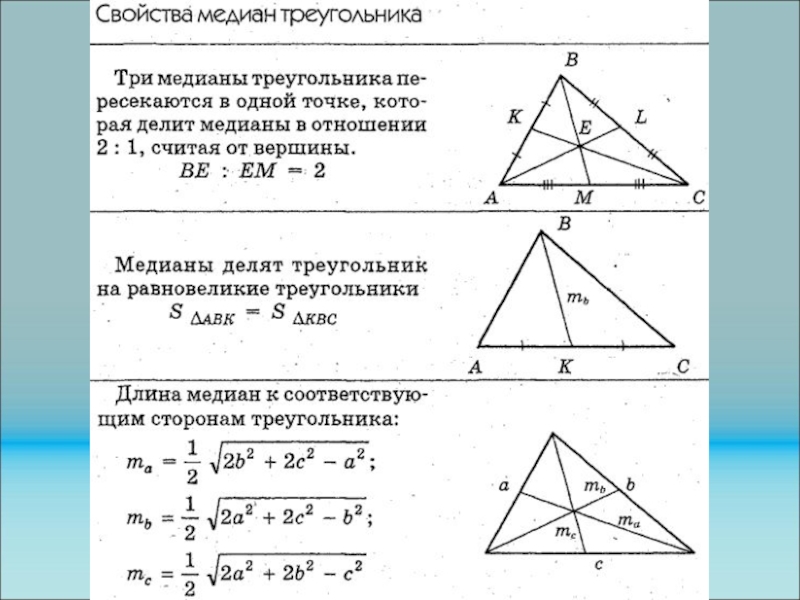
Доказать, что возможно построить треугольник, стороны которого равны медианам
произвольного треугольника АВС. Замечание. Треугольник не всегда возможно построить.
Решение. Обозначим середины сторон ВС через L, АС через М и АВ через K, выразим векторы, представляющие медианы треугольника АВС, т.е. АL, CK и BM, через векторы a, b, c. Тогда АL=АВ+ВL=с+0,5а. Аналогично
Слайд 146Пример
BM=а+0,5b, CK=b+0,5c. Необходимым и достаточным условием образования тремя векторами
треугольника является равенство нулю их суммы. Тогда проверим для медиан
АL+BM+CK=с+0,5а+а+0,5b+b+0,5c=
1,5(а+b+c)=0. Мы доказали утверждение.
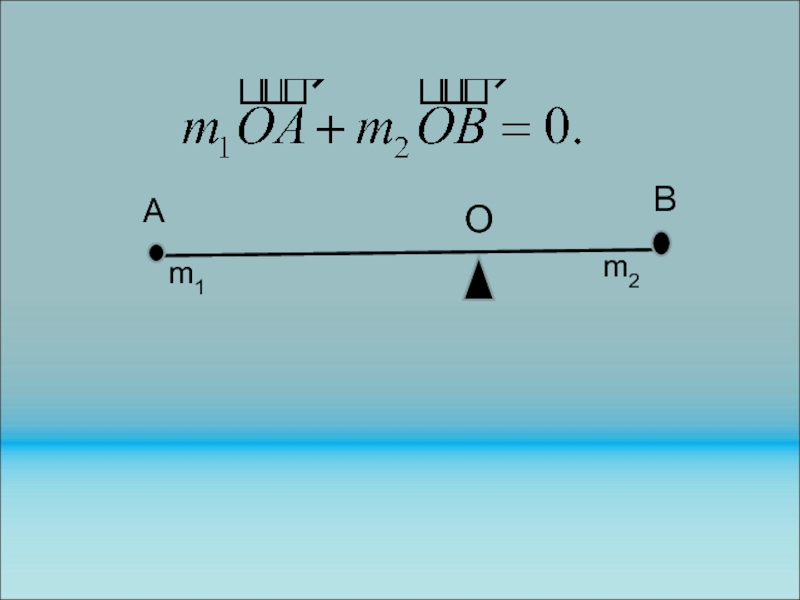
Выше говорилось о делении медиан т. Е.
Образуем рычаг из двух точек массой m1 и m2, соединенных невесомым стержнем. Правило рычага: ОА/ОВ=m2/m1 или m1ОА=m2ОВ. Векторно это запишем так
Слайд 148Пример
Теперь понятно как определить центр масс для произвольного числа точек.
О делении отрезка в данном отношении будет сказано ниже.
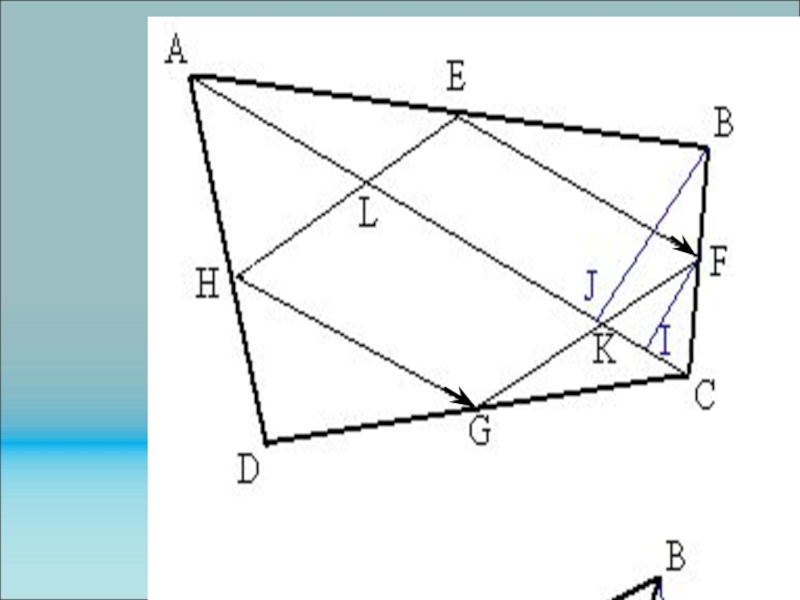
Задача. Доказать, что середины сторон произвольного (возможно расположенного в пространстве !)
Слайд 149Пример
четырехугольника являются вершинами параллелограмма.
Решение. Пусть E, F, G,
H – середины сторон четырехугольника АВСD (см. слайд).
Слайд 151Решение
Тогда EF-HG= EF+GH =(EB+BF) +(GD+DH)=0,5(AB+BC+CD+DA)=
=0,5AA=0.
Потому что
вектор AA равен нулю. Таким образом, EF=HG, т.е. противоположные стороны
четырехугольника EFGH равны и параллельны. Следовательно, EFGH - параллелограмм. Заметим, что диагональ АС (и диагональ ВD) делит параллелограмм EFGH на два других.
Слайд 152Замена базиса
Пусть (е1, е2, е3) и (g1, g2,
g3) – два базиса. Векторы второго базиса, как векторы пространства,
разлагаются по первому базису
g1 = c11е1 + с21е2 + с31е3,
g2 = c12е1 + с22е2 + с32е3,
g3 = c13е1 + с23е2 + с33е3.
Коэффициенты cij этих разложений образуют матрицу, которая называется матрицей перехода от базиса е к базису g. Забегая вперед, скажем, что матрица перехода невырождена.
Слайд 153 Пример. Рассмотрим пространство многочленов Мn. В этом пространстве
многочлены 1, х, х2,…хn образуют базис, т.к. они линейно независимы.
Координатами многочлена аnхn + аn-1хn-1 +… + а1х+ а0 служат его коэффициенты а0, а1,… , аn. Размерность пространства равна n+1.
Аналогично можно рассмотреть множество матриц, размером mn, образующих пространство R mn. В этом пространстве матричные единицы, т.е. матрицы Е11, Е12,… (в матрице Еij все элементы нулевые, кроме одного в позиции (i,j), равного единице) образуют естественный базис. Например, для 3-х мерного случая
Слайд 154Пример естественного базиса (матричные единицы)
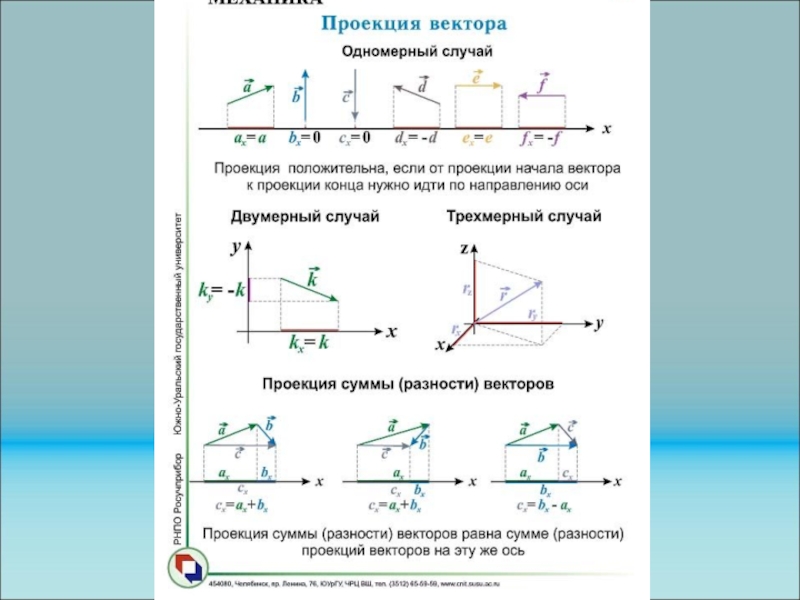
Слайд 155Проекция вектора
Проекцией вектора на прямую
(плоскость) является направленный
отрезок, образованный проекциями его начальной и конечной точек. Проекции вектора
в пространстве обладают свойством линейности. Обозначение пр (pr).
Проекция вектора на ось L выражается через его модуль и угол наклона к оси формулой
проекция равна - прLr =| r| cos .
Слайд 157Пример
Пример. Найти проекцию вектора а={4, 0, 1} на вектор
b={-2, 1, 2}.
Решение. Для нахождения проекции используем скалярное
произведение (суммирование попарных произведений координат).Проекция равна
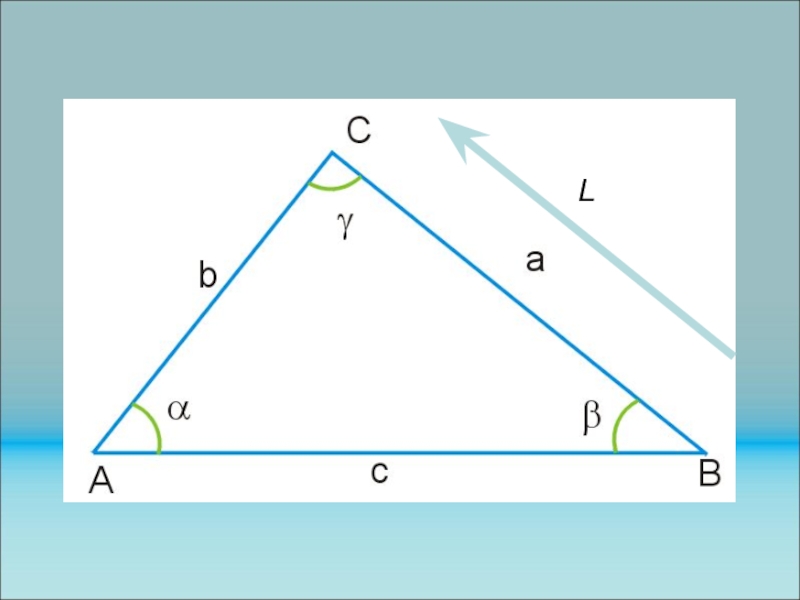
Слайд 158Формула проекций
Пример. Доказать, что в любом треугольнике имеет место
соотношение
a= bcosC+ccosB = bcos+ccos
(формула проекций – следующий слайд).
Решение. Положим а=ВС, b=АС, c=ВА и обозначим через L ось, имеющую направление вектора а. Вектор b образует с осью L угол , вектор с образует с осью L угол , а вектор а образует с этой осью угол, равный
Слайд 160Формула проекций
нулю. Поэтому прLа =|а|, прLb =|b|cos, прLc =|c|cos
. Так как длина вектора а равна сумме длин проекций
векторов b и с, то формула доказана.
Мы видим, что для эффективного решения задач на проекции нам требуется скалярное произведение (см. ниже).
Слайд 161Задача
Пример. Дан вектор r=ОА ={х , у}. Найти
координаты вектора
ОВ, получающегося из вектора ОА поворотом на угол .
Решение. Пусть ОВ= {х1 , у1}.Перейдем
к новому базису, полученному из исходного поворотом на угол , т.е. повернем систему. Находим координаты вектора в этом базисе. Они равны (!) x1 =хcos –ysin ,
y1 =xsin +ycos .
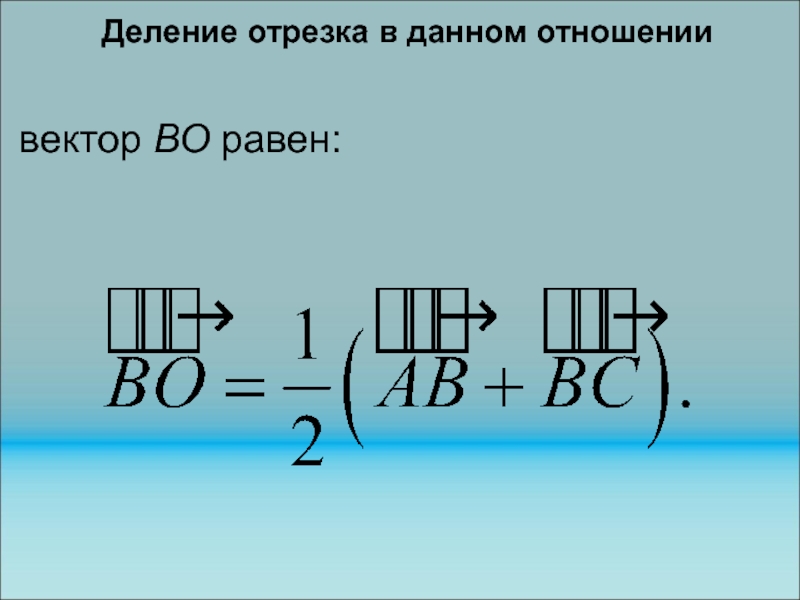
Слайд 163Деление отрезка в данном отношении
Нижеследующие предложения часто применяются при
решении задач.
Предложение 1. Если векторы а и b параллельны,
(а 0), то существует такое число k, что b= k а.
Предложение 2. Пусть А, В, С – три точки, причем А В и O – произвольная четвертая точка. Точка С только тогда лежит на прямой АВ, когда существует такое число , что OС= OА +(1- )OВ.
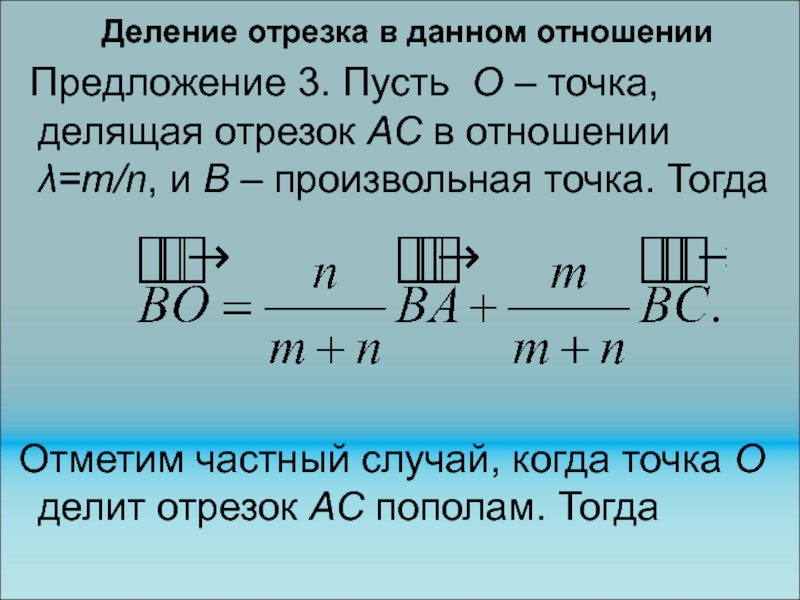
Слайд 164Деление отрезка в данном отношении
Предложение 3. Пусть O –
точка, делящая отрезок АC в отношении =m/n, и B –
произвольная точка. Тогда
Отметим частный случай, когда точка O делит отрезок АC пополам. Тогда
Слайд 166Деление отрезка в данном отношении
вектор ВО равен:
Слайд 167Единичным вектором, как говорилось, является вектор, у которого длина равна
единице (например, лишь одна компонента равна единице, а остальные равны
нулю).
Вектор можно записывать в виде столбца
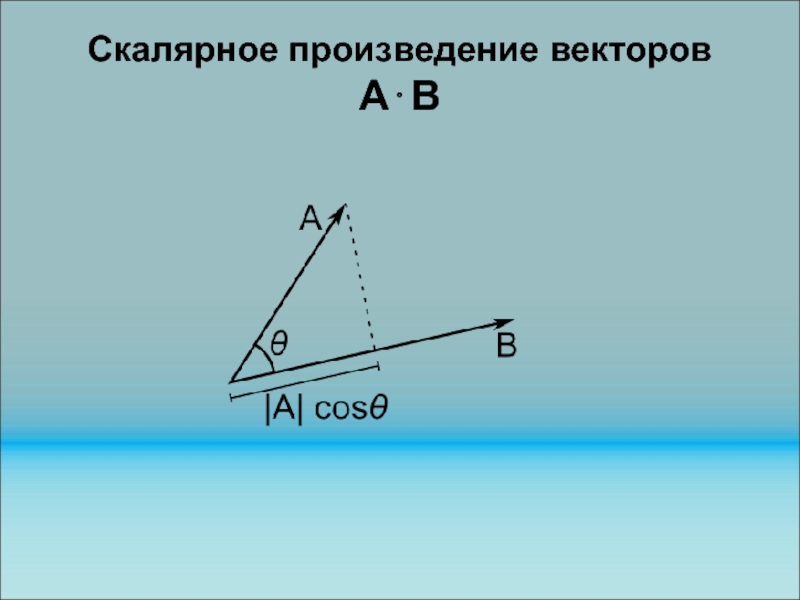
Слайд 168Скалярное произведение векторов
Векторы можно перемножать. Допустим, что у нас имеется
два вектора
и обозначает угол между этими векторами.
Тогда число, полученное по формуле
Слайд 169Скалярное произведение векторов
называют скалярным произведением векторов и обозначают также точкой
a b или угловыми скобками a, b . Скалярное
произведение векторов является скалярной величиной, т.е. числом. Оно может быть вычислено простым умножением модуля вектора a на проекцию вектора b на a (праb)или перемножением соответствующих компонент векторов и сложением результатов (суммирование попарных произведений):
Слайд 171Скалярное произведение векторов
Векторы a и b называются ортогональными, если их
скалярное произведение равно нулю a b = 0. Скалярное произведение
линейно.
Скалярное произведение позволяет нам ОПРЕДЕЛИТЬ норму (длину) вектора:
Косинус угла между векторами равен:
Слайд 172Скалярное произведение векторов
Пример. Пусть А, В, С, D – произвольные
точки плоскости или пространства. Доказать, что сумма скалярных произведений векторов,
соединяющих точки, равна нулю:
Решение. Выразим участвующие векторы через векторы a = АВ, b= ВС, с= СD и воспользуемся линейностью скалярного произведения:
Слайд 173Скалярное произведение векторов
Пример. Пусть заданы векторы р(a, b) и q(c,
d), тогда синус угла между ними может быть вычислен по
формуле:
(1)
где - определитель, составленный из координат векторов (см. следующий слайд)
Слайд 174Угол между векторами
Определитель равен:
Замечание
Слайд 175Угол между векторами. Доказательство
Откуда следует справедливость формулы.
Из этой формулы
вытекает утверждение.
Слайд 176Площадь параллелограмма
Утверждение. Пусть ABCD произвольный параллелограмм, заданный векторами р(a, b)
и q(c, d). Тогда площадь S параллелограмма равна .
В
самом деле:
Замечание. Площадь треугольника равна1/2
Скалярное произведение позволяет записать по-новому уравнение плоскости, что дает возможность наглядно мыслить: r N=d. Здесь
Слайд 177Скалярное произведение
вектор N - ортогонален плоскости. Скалярное произведение отражает широко
распространенный способ взаимодействия векторов. Например, работа силы F на перемещении
ds равна
Скалярное произведение – удобный инструмент решения задач.
Пример. Произведение единичных векторов a(cos , sin ) и b(cos , sin ) дает формулу
Слайд 179ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Скалярное произведение ставит в соответствие векторам число. Рассмотрим
«произведение», которое ставит в соответствие двум векторам не число, а
вектор. Векторное произведение (обозначим ) — это вектор, перпендикулярный плоскости, построенной по двум сомножителям (векторам), являющийся результатом определенной операции и равный площади параллелограмма, построенного на этих векторах.
Слайд 180ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Если мы введем на множестве векторов вторую операцию
(умножение), то получим алгебраическую структуру – кольцо. Заметим, что в
этом случае будет выполняться т.н. тождество Якоби:
Всякое кольцо, в котором произведение вектора самого на себя хх=0 и справедливо тождество Якоби, называется кольцом Ли.
Слайд 181ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Векторным произведением векторов a и b называется вектор
с такой, что:
- модуль с равен
вектор с ортогонален каждому из
векторов a и b ,
вектор с направлен так, что тройка векторов a, b, с – правая.
Обозначение: [a, b] или ab.
Векторы коллинеарны только тогда, когда [a, b] =0
Слайд 182ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Векторное произведение описывает многие физические явления. Например, моментом
силы F относительно точки О называется вектор, равный М=r F.
Тонкость определения векторного произведения заключается в том, что оно как бы ощущает ориентацию пространства (меняет направление при замене левой системы координат на правую). Такие векторы называются аксиальными. Обычные векторы в физике называются полярными.
Слайд 183ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Векторное произведение – удобный инструмент решения задач.
Пример.
Векторное произведение векторов (a+b) (a-b) приводит к
(a+b) (a-b)=-2ab,
что означает, что площадь параллелограмма, построенного на диагоналях, в два раза больше площади исходного параллелограмма. Уравнение прямой, параллельной вектору а и проходящей через точку b(конечную), есть векторное произведение (r-b) а=0.
Слайд 185ВЕКТОРНОЕ ПРОИЗВЕДЕНИЕ
Векторное произведение векторов a(а1, а2, а3) и b(b1,
b2, b3) в декартовых координатах равно (обозначим его в квадратных
скобках, а определитель запишем по формуле Лапласа):
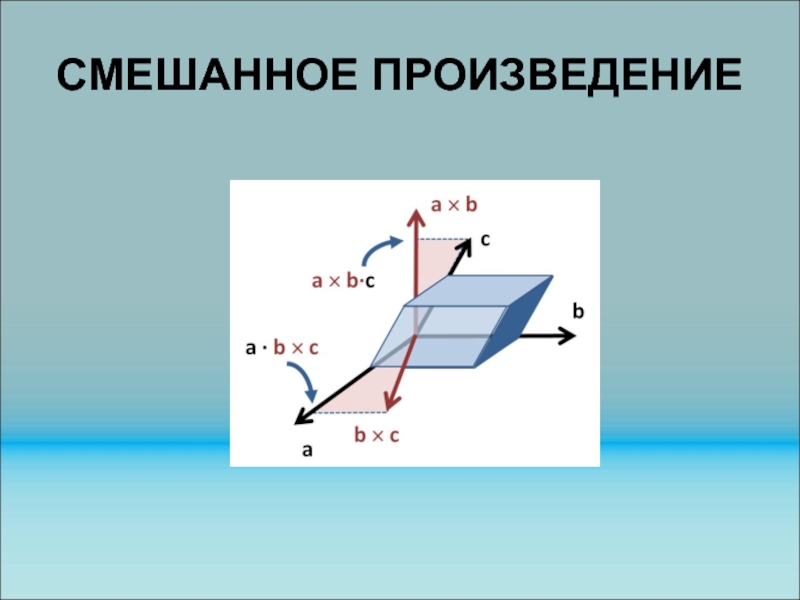
Слайд 186СМЕШАННОЕ ПРОИЗВЕДЕНИЕ
Сме́шанное произведе́ние векторов а , b и с
а(bс) обозначается (а, b, с) равно скалярному произведению (т.е. это-число)вектора
а на вектор, который есть векторное произведение b на с.
Векторы компланарны только тогда, когда (а, b, с) =0
Модуль смешанного произведения численно равен объёму параллелепипеда, образованного векторами а , b и с.
Слайд 188Запись смешанного произведения с помощью определителя
Слайд 189Другая форма записи СМЕШАННОГО ПРОИЗВЕДЕНИЯ
Слайд 190Равенство нулю определителя
Здесь в вертикальных отрезках представлен определитель матрицы (см.
ниже). Можно заметить, что если хотя бы два вектора пропорциональны,
т.е. линейно зависимы, то объем и определитель равны нулю. Если речь зашла об определителе, то сразу можно сказать, что определитель треугольной матрицы равен произведению диагональных элементов.
Слайд 191Определитель треугольной матрицы
Например.
Рассмотрим пример нахождения определителя. Мы можем к любой
строке прибавить строку. Воспользуемся этим для преобразования определителя к
Слайд 192треугольному виду( из 2-й строки вычтем 1-ую):
Слайд 193Значение представленного ниже определителя не надо искать, т.к. его величина
равна нулю(!).Третий столбец пропорционален первому.
Слайд 194Свойства смешанного произведения
Для любых векторов справедливо:
(а, b, с)= (b, с,
а)=(с, а, b)= -(b, а, с)=-(а, с, b)= -(с, b,
а).
Смешанное произведение (как и векторное) линейно по каждому сомножителю.
Пример. Вывести условие того, чтобы четыре точки А(х1 , у1, z1 ), B(х2, у2, z2 ), C(х3, у3, z3 ) и D(х4 , у4, z4 ) лежали в одной плоскости.
Слайд 195Четыре точки в одной плоскости
Искомое условие равносильно условию компланарности векторов
АВ, АС и АD. Тогда справедливо:
Слайд 196Ортогональное проектирование
Зададим линейное векторное подпространство L пространства V. Вектор пространства
х представим в виде суммы х= хn + хm, где
хn – нормальная составляющая вектора х относительно подпространства L.Тогда нормальная составляющая равна
Слайд 197Прямая и плоскость
Прямая определяется как множество точек, удовлетворяющих линейному уравнению,
например а1 x1 + а2 x2 =b. При этом тройки
(а1, а2 , b) и (а1, а2 , b) описывают одну и ту же прямую.
Плоскость можно задать различными уравнениями, например,
х + у + z +d=0 (что не очень ясно, здесь нормаль – {, , }), либо векторно
r N=d, ( N={, , }- нормаль), либо
r = а+ b +М,- параметрическое, плоскость проходит через точку М и ортогональна аb.
Слайд 198Прямая и плоскость
Второе уравнение позволяет проверить, принадлежит ли предъявляемая точка
r = {х, у, z } рассматриваемой плоскости. Для этого
нужно проверить равенство r N=d. Параметрическое уравнение позволяет «генерировать» точки плоскости, выбирая параметры , .
Приведенная двойственность уравнений характерна для математики вообще. Из одного описания нетрудно получить другое.
Рассмотрим уравнение прямой на плоскости.
Слайд 199Прямая
На плоскости уравнение прямой, проходящей через т. М(х0 , у0
) с направляющим вектором а=(m, n) может быть записано:
Здесь m
или n могут быть равны нулю (но это не деление).
Уравнение прямой, проходящей через две различные точки (х0 , у0 ) и (х1, у1) имеет вид:
Слайд 200Прямая и плоскость (канонические уравнения)
Уравнение плоскости, проходящей через т. (х0
,у0 , z0) с направляющими векторами а=(m1, n1, k1), b=(m2,
n2, k2) имеет вид:
Уравнение прямой, проходящей через две различные точки и имеет вид
Слайд 202Параметрические уравнения
Уравнение прямой, проходящей через точку М(r0) с направляющим вектором
а=(m, n) имеет вид:
r=r0 +ta
Здесь t - параметр.
В координатной форме
уравнение прямой
Уравнение прямой, проходящей через две различные точки и имеет вид
Слайд 203Параметрические уравнения
Уравнение плоскости, проходящей через точку М(r0) с направляющими векторами
а=(m1, n1, k1), b=(m2, n2, k2) имеет вид:
r=r 0 +
a+ b
Здесь и - параметры.
В координатной форме
Уравнение прямой, проходящей через две различные точки и имеет вид
Слайд 204Прямая
Линия на плоскости является прямой только тогда, когда она определяется
уравнением
Это уравнение называется общим уравнением прямой.
Уравнение прямой в пространстве:
Слайд 205Прямая
Общее уравнение прямой в пространстве:
Запишем подобные два уравнения для прямой
на плоскости
Возможны три варианта. Либо прямые не имеют общих
точек, либо совпадают, либо пересекаются в одной точке. Т.е. мы имеем решение системы двух уравнений.
Слайд 206Чтобы найти решение и исключить x2, умножим первое уравнение на
a22 и из полученного уравнения вычтем второе уравнение системы, умноженное
на a12
Обозначим детерминант = a11a22 – a12a21 0, а частные определители обозначим
Слайд 2071 = b1a22 – b2a12 и 2 = b2a11 –b1a21
В
этих обозначениях равенства (2) перепишутся так:
Слайд 208Из (3) следует, что при 0 наша система
имеет единственное решение, определяемое формулами (Крамера)
Величина называется определителем системы
или матрицы второго порядка- (обозначается в вертикальных отрезках), которая имеет геометрическую интерпретацию – площадь параллелограмма
Слайд 209Если же определитель = 0, то тогда
и для существования решения
необходимо и достаточно, чтобы это отношение равнялось отношению b1/b2.
Если рассматривается
семейство {аi1 x i1 + а i2 x i2 =bi} более двух уравнений (?), то возможно, что прямые совпадают, когда (аi1 , а i2 , bi )= (аi1, а i2 , bi ), либо все прямые проходят через одну точку (единственное решение). Это выполнится когда величины
Слайд 210
не зависят от выбора i и j. В остальных случаях
«решение» пусто.
В итоге мы получили следующий результат: решением системы линейных
равенств является аффинное множество.
Слайд 211Прямая
Итак, общее уравнение прямой в пространстве:
т.е. пересечение двух
плоскостей. Уравнение прямой, проходящей через две данные точки (векторное):
Слайд 212Прямая
Уравнение прямой, проходящей через данную точку перпендикулярно к плоскости
(r, N)+D=0:
Кратчайшее расстояние между двумя прямыми, заданными в
канонической форме:
Слайд 213Кратчайшее расстояние
Обращение в нуль числителя есть условие пересечения прямых.
Слайд 214Четыре плоскости проходят через одну точку, если
Условия параллельности:
двух прямых: R1×R2
=0,
двух плоскостей: N1×N2 =0,
Прямой и плоскости: R N =0,
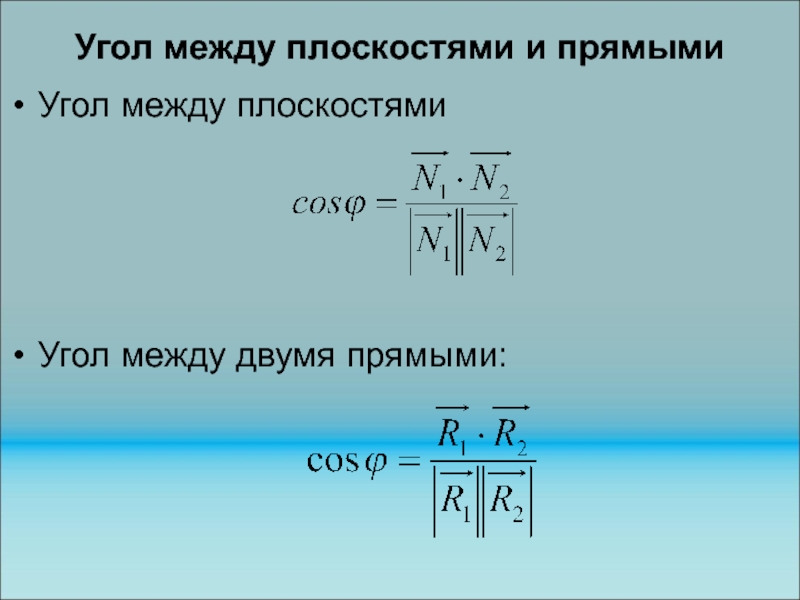
Слайд 215Угол между плоскостями и прямыми
Угол между плоскостями
Угол между двумя
прямыми:
Слайд 216Угол между плоскостями и прямыми
Угол между прямой и плоскостью
Условия перпендикулярности:
двух
прямых: R1R2 =0,
двух плоскостей: N1 N2 =0,
Прямой и плоскости: R
× N =0,
Слайд 217АЛГЕБРАИЧЕСКИЕ ЛИНИИ ВТОРОГО ПОРЯДКА
Эллипс, гипербола и парабола
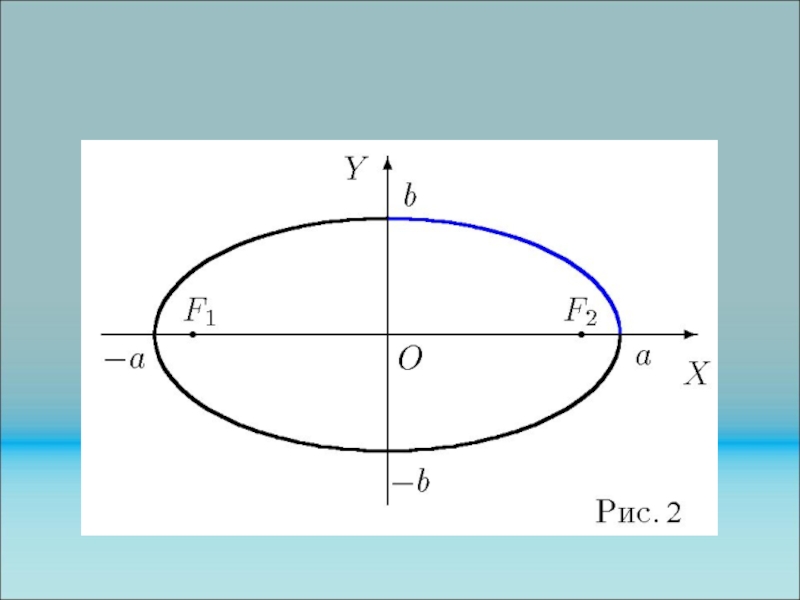
Эллипс. Эллипсом называется геометрическое
место точек плоскости, для которых сумма расстояний от двух фиксированных
точек F1 и F2 есть постоянное число. Точки F1 и F2 называются фокусами эллипса.
Слайд 219ЭЛЛИПС
Введем каноническую систему координат. Примем за начало координат середину отрезка
F1F2, за ось абсцисс -прямую F1F2, ось ординат перпендикулярна оси
абсцисс. Фокусы в канонической системе координат, имеют координаты (-с, 0) и (с, 0). Уравнение эллипса в канонической системе координат имеет вид:
Слайд 220ЭЛЛИПС
Число =с/а называется эксцентриситетом эллипса. Эксцентриситет меньше единицы и равен:
Слайд 221ГИПЕРБОЛА
Гиперболой называется геометрическое место точек, для которых абсолютная величина разности
расстояний от двух фиксированных точек F1 и F2 плоскости есть
постоянное число. Обозначим это число 2а. Точки F1 и F2 называются фокусами гиперболы, а расстояние между ними – фокальным расстоянием.
Слайд 223ГИПЕРБОЛА
Введем каноническую систему координат так же, как для эллипса. Фокусы
в канонической системе координат, имеют подобные координаты (-с, 0) и
(с, 0). Точки (-а, 0) и (а, 0) – вершины гиперболы. Уравнение гиперболы в канонической системе координат имеет вид:
Слайд 224ГИПЕРБОЛА
Число =с/а называется эксцентриситетом гиперболы. Эксцентриситет больше единицы и равен:
Слайд 225ПАРАБОЛА
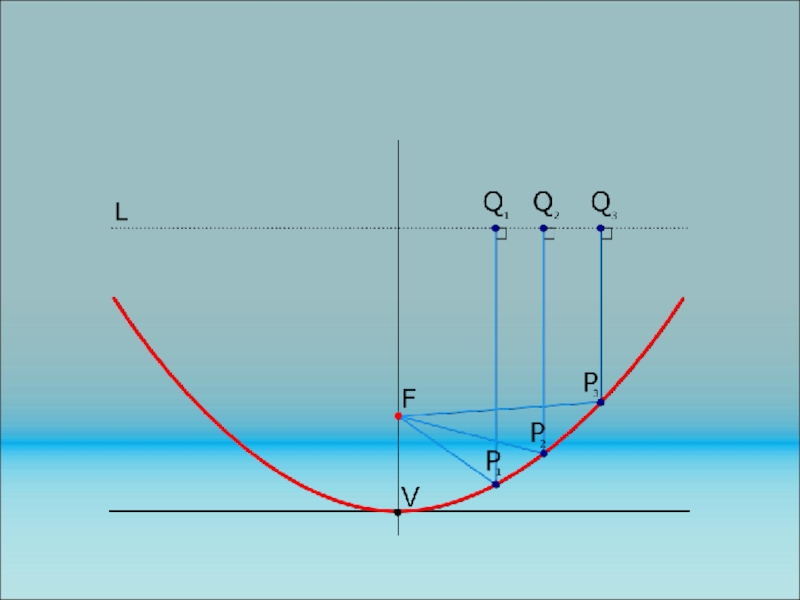
Параболой называется геометрическое место точек, для которых расстояние до некоторой
фиксированной точке F равно расстоянию до некоторой фиксированной прямой d,
не проходящей через F. Точка F называется фокусом параболы, а расстояние от фокуса до прямой d называется фокальным параметром и обозначается р. Уравнение параболы в канонической системе координат имеет вид:
у2 = 2рх