Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Реферат на тему Методика изучения трехмерных геометрических фигур
Содержание
- 1. Реферат на тему Методика изучения трехмерных геометрических фигур
- 2. Цель – изучить и проанализировать программы начальных
- 3. Задачи и содержание геометрического материала в начальной
- 4. В настоящее время создаются учебные программы по
- 5. Методика изучения геометрического материала
- 6. Заботясь о развитии
- 7. Первым этапом формирования геометрических представлений пространственных фигур
- 8. На следующем этапе вводятся понятия. Определения понятий
- 9. Следующий этап: получение модели, если это возможно.При
- 10. После учащиеся на основе наглядных представлений, знакомятся
- 11. Затем проводится работа по введению понятия пересечения
- 12. Еще одним из направлений в рассмотрении объемных
- 13. Анализ программ по математике на предмет содержания геометрического материала
- 14. В программе М.И. Моро трехмерные геометрические фигуры
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
- 23. В учебниках Н.Б. Истоминой знакомство с объемными
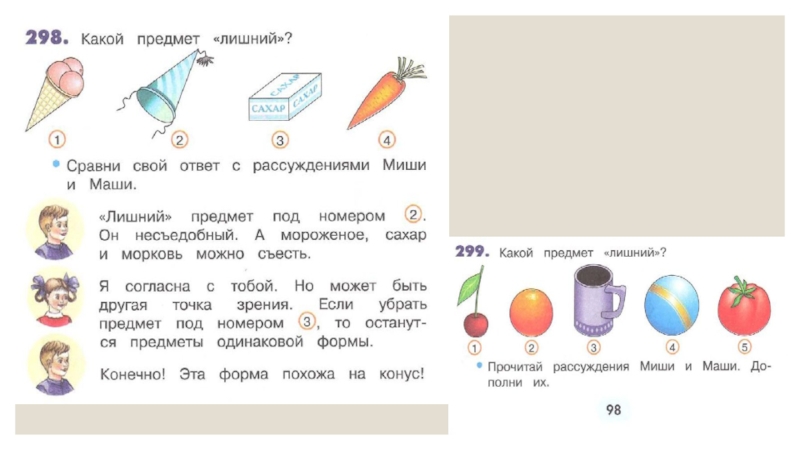
- 24. В 3 классе 2 части в разделе
- 25. 2 класс 1 часть
- 26. Слайд 26
- 27. 2 класс 2 часть
- 28. Слайд 28
- 29. Слайд 29
- 30. Слайд 30
- 31. Слайд 31
- 32. 3 класс 1 часть
- 33. Слайд 33
- 34. Слайд 34
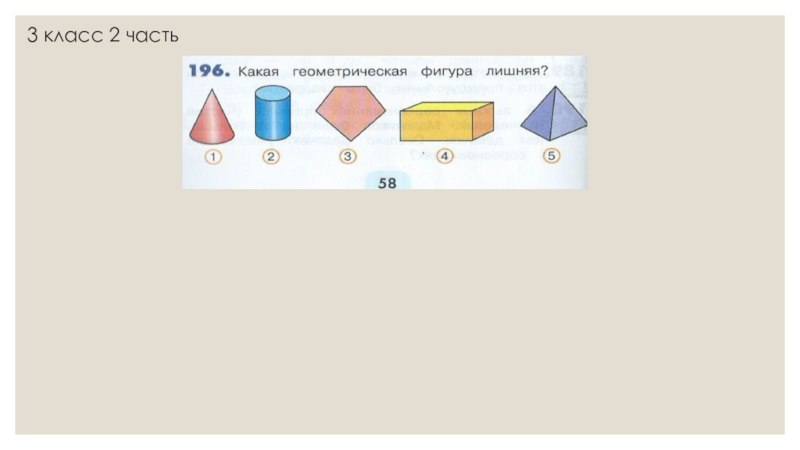
- 35. 3 класс 2 часть
- 36. Слайд 36
- 37. Слайд 37
- 38. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Реферат на тему
«Методика изучения трехмерных геометрических фигур»
Выполнила студентка группы ЗНОЛу-117
Качинская В.А.
Слайд 2Цель – изучить и проанализировать программы начальных классов на предмет
изучения трехмерных геометрических фигур.
Объект исследования: процесс развития пространственного мышления
младших школьников. Предмет исследования: методика изучения объемных геометрических фигур как средство развития пространственного мышления.
Слайд 3Задачи и содержание геометрического материала в начальной школе
• формирование геометрических
представлений об образах геометрических фигур, их элементов, отношений между фигурами
и их элементами;• выработка практических умений и навыков в измерениях и построении простейших геометрических фигур с помощью чертежных инструментов;
• развитие пространственных представлений, воображения и пространственного мышления учащихся;
• обогащение математического словарного запаса, развитие речи учащихся.
Слайд 4В настоящее время создаются учебные программы по геометрии, которые при
всем многообразии образовательных целей решают три задачи.
1. Преодоление существенного
разрыва между изучением плоских и пространственных фигур. 2. Создание у учащихся гибких, многомерных пространственных образов, включающихся в единстве топологические, проективные, метрические свойств и отношения изучаемых объектов.
3. Сочетание инвариантного и вариантного учебного материала, позволяющего учитывать познавательный профиль ученика, его индивидуальную избирательность к виду и форме предлагаемых заданий и упражнений
Слайд 5Методика изучения геометрического материала
В курсе математики
начальной школы геометрический материал излагается фрагментарно и не представляет собой
систему. Чтобы ввести школьника в мир геометрии на основе рассмотрения окружающего мира, необходимо учить его при восприятии предметов выделять и абстрагировать их геометрические свойства, видеть в них модели геометрических объектов, т.е. создавать геометрические образы. Именно они являются основой геометрических понятий. В начальной школе у учащихся формируются обобщенные представления или образы- понятия. Сформированность геометрического понятия предполагает умение рассматривать его в системе понятий, а также владение кванторами и законами логики, что возможно только в основной школе и требует определенной логической подготовки младших школьников. Поэтому, согласно принципу природосообразности, разумно предлагать учащимся не определения, а описания понятий, которые направлены на создание геометрических образов.
Слайд 6 Заботясь о развитии ребенка при изучении
геометрии, учитывая естественное развитие, целесообразно организовывать процесс обучения геометрии через
реализацию следующих этапов:- актуализация знаний;
- введение понятия;
- получение модели, если это возможно;
- некоторые свойства геометрических фигур;
- связи с ранее изученными понятиями;
- применение знаний в различных ситуациях.
Слайд 7Первым этапом формирования геометрических представлений пространственных фигур – восприятие геометрических
фигур как целостного образа. На этапе актуализации знаний выделяем в
жизненной ситуации объект определенной формы. Эту работу можно вести в следующих направлениях:Сравнение различных реальных предметов и выделение групп предметов, сходных по форме.
Подбор других подходящих по форме предметов к выделенным группам.
Сравнение выделенных по сходству формы предметов с моделями объемных геометрических фигур и выбор соответствующих моделей, знакомство с названиями выбранных моделей.
Слайд 8На следующем этапе вводятся понятия. Определения понятий детям не сообщаются,
и соответственно от учащихся не требуется их знания.
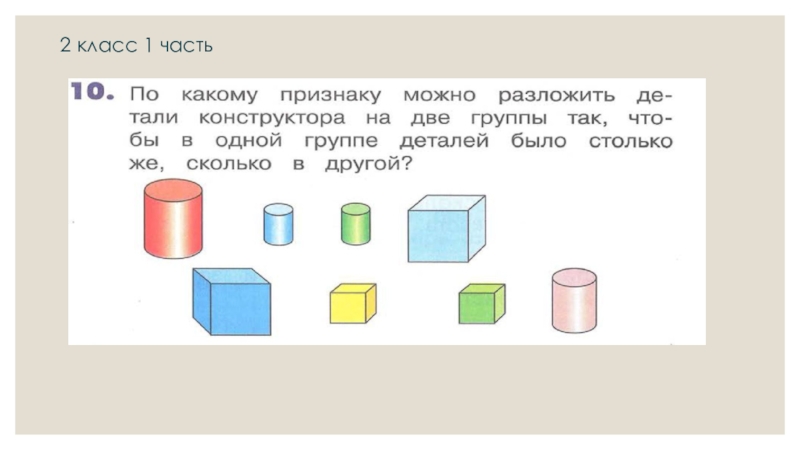
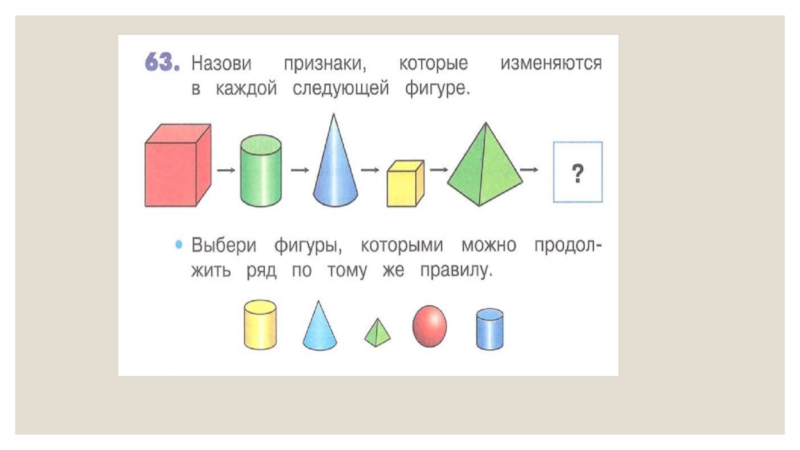
Для усвоения
существенных признаков понятия целесообразно использовать такие приемы как сравнение и классификация.Дети должны научиться практически использовать соответствующие признаки при узнавании различных фигур, их классификацию.
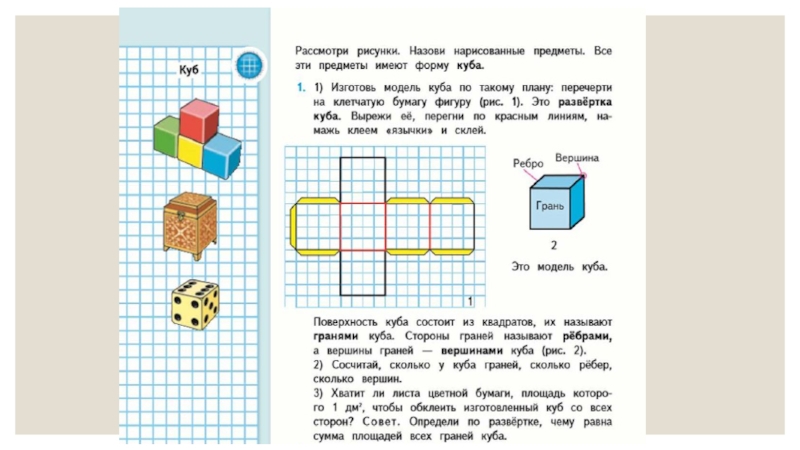
Следующей задачей после знакомства- это узнать, как называются элементы куба (грани, вершины, ребра) их количество.
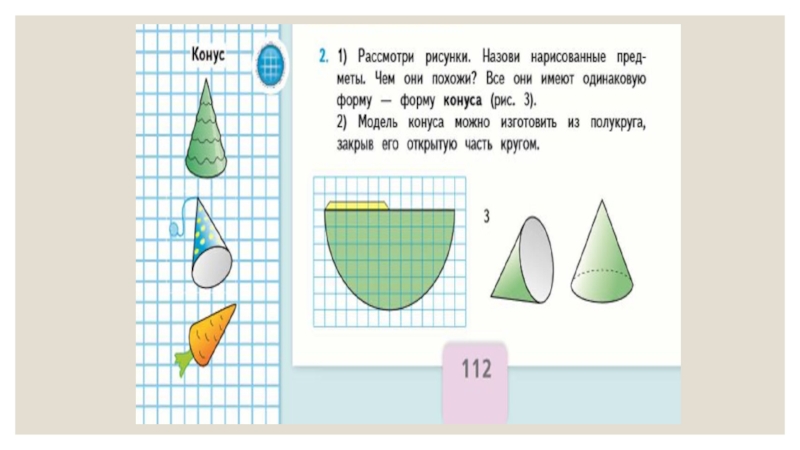
Данное направление позволит связать в единое целое объемные и плоскостные фигуры, где плоскостные фигуры выступят в своей естественной для трехмерного пространства роли - части объемного тела. Например, круг выступит как часть поверхности конуса или цилиндра, прямоугольник - как часть поверхности призмы, треугольник - пирамиды и т.д.
Слайд 9Следующий этап: получение модели, если это возможно.
При выполнении конструктивных заданий
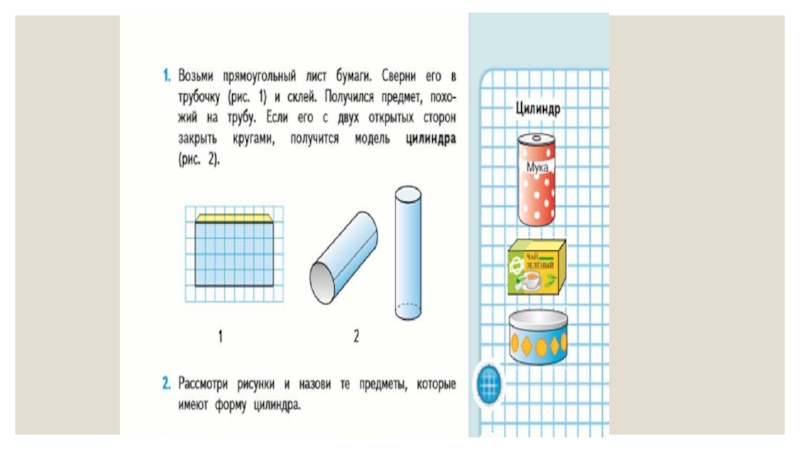
дети работают с различными материалами: конструктором, палочками, ленточкой, листом бумаги.
Развитие пространственного мышления невозможно отделить от формирования умений мысленно представлять различные положения предмета, изменения его формы и положения в зависимости от точки зрения, различных поворотов и трансформаций, умением зафиксировать это представление на изображении. Известно, что базой для развития пространственного мышления являются пространственные представления, которые отражают соотношения и свойства реальных предметов, то есть свойства трехмерного видимого или воспринимаемого пространства.Слайд 10После учащиеся на основе наглядных представлений, знакомятся с понятием «часть
фигуры». Можно рассмотреть вопросы:
назови известные нам различные части многогранников
и тел вращения. «отрежем» от куба некоторую часть; какими известными вам фигурами может быть эта часть?
назови части плоских фигур.
Слайд 11Затем проводится работа по введению понятия пересечения фигур. Сначала с
учащимися рассматриваются упражнения:
возьмите два одинаковых куба и приложите их
друг к другу так, чтобы какая-нибудь часть одного куба была одновременно частью и другого куба, т.е. была общей частью этих двух кубов; покажите случай, когда общей частью будет вершина, ребро грань, часть ребра, часть грани, точка, отрезок.может ли общей частью двух кубов быть прямая, луч, плоскость?
с помощью моделей покажите случай, когда пересечением двух равных кубов является вершина, точка, ребро, отрезок, квадрат, грань, треугольник.
Слайд 12Еще одним из направлений в рассмотрении объемных фигур является сравнение
моделей различных наименований. Этот материал изучается на ознакомительном уровне. Например,
сравнивая модели шара, цилиндра, конуса, учащиеся находят общее для них – это способность катиться. Различия этих тел в том, что у шара нет ни вершин, ни оснований, у цилиндра – два основания, но нет вершин, у конуса – одно основание и одна вершина. Так же аналогично рассматриваются и сравниваются другие тела: пирамида и конус, пирамида и призма, цилиндр и призма и др.Слайд 14В программе М.И. Моро трехмерные геометрические фигуры изучаю в 4
классе 4 четверти в разделе «Материал для расширения и углубления
знаний»Учащийся получает возможность научится:
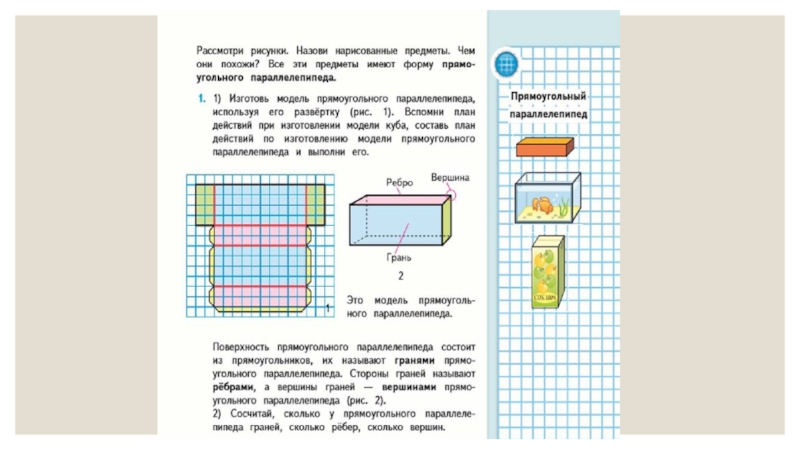
распознавать, различать и называть геометрические тела: прямоугольный параллелепипед, пирамиду, цилиндр, конус;
изготавливать модель куба, прямоугольного параллелепипеда, пирамиды, конуса, цилиндра, шара;
сравнивать геометрические тела;
находить грань, ребро, вершину куба, прямоугольного параллелепипеда, пирамиды
Слайд 23В учебниках Н.Б. Истоминой знакомство с объемными геометрическими фигурами начинается
во втором классе.
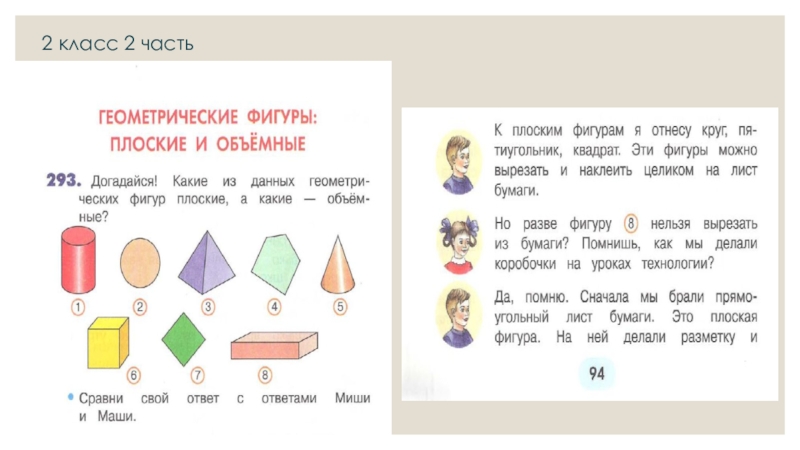
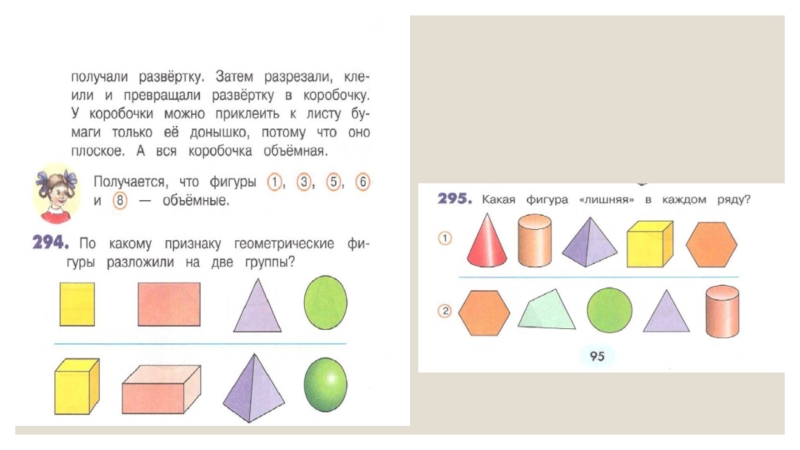
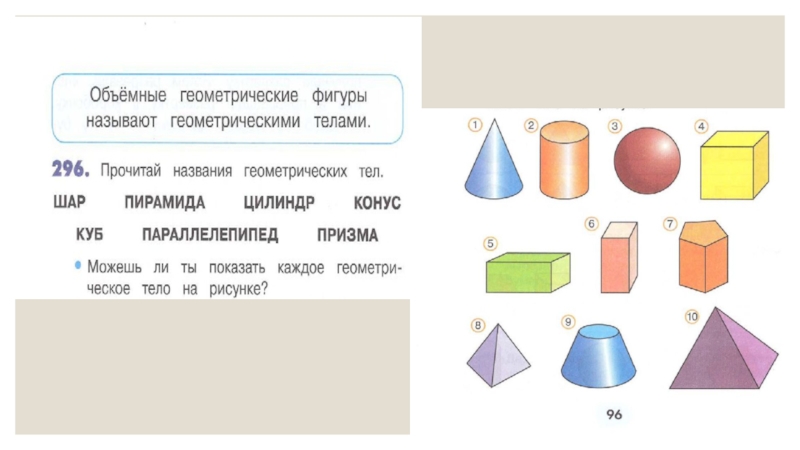
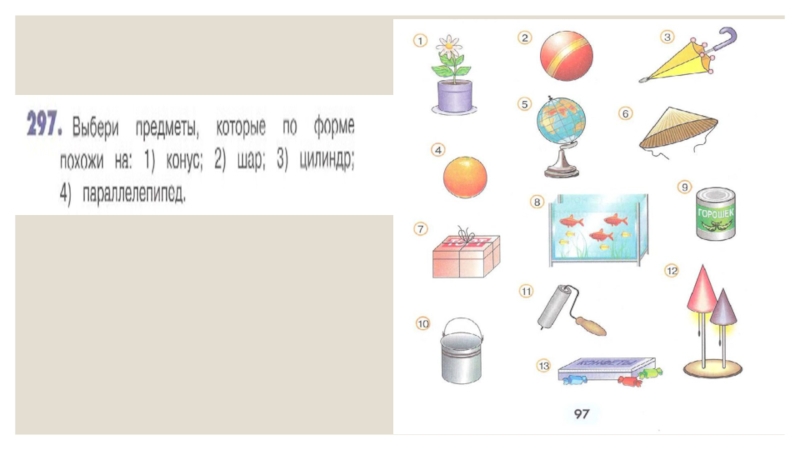
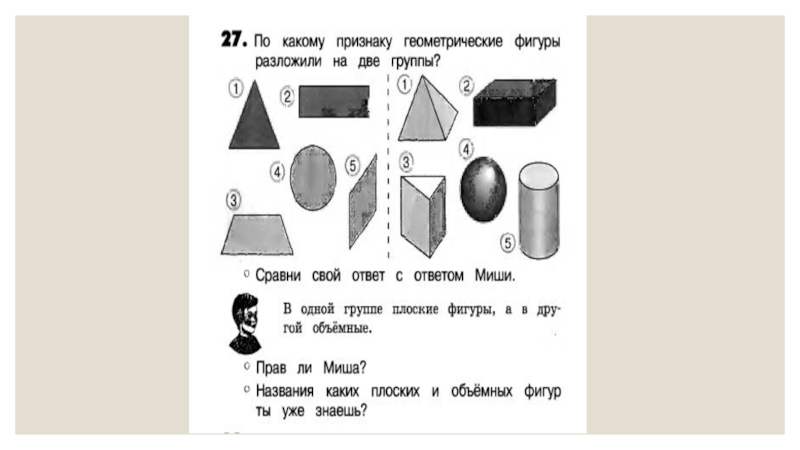
Во втором классе дается представление о объемных геометрических
фигурах: шар, пирамида, цилиндр, конус, куб, параллелепипед без введения понятий.В разделе «Геометрические фигуры: плоские и объемные» учащимся предлагаются задания на распознавание, целью которых является умение различать объемные геометрические фигуры и существенные признаки.