Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Рекурсивные структуры в алгоритмах
Содержание
- 1. Рекурсивные структуры в алгоритмах
- 2. Рекурсия — способ общего определения множества объектов или
- 3. В искусстве рекурсия выглядит примерно так :
- 4. Или как в народной песенке:У попа была
- 5. В программировании рекурсия — вызов функции (процедуры) из
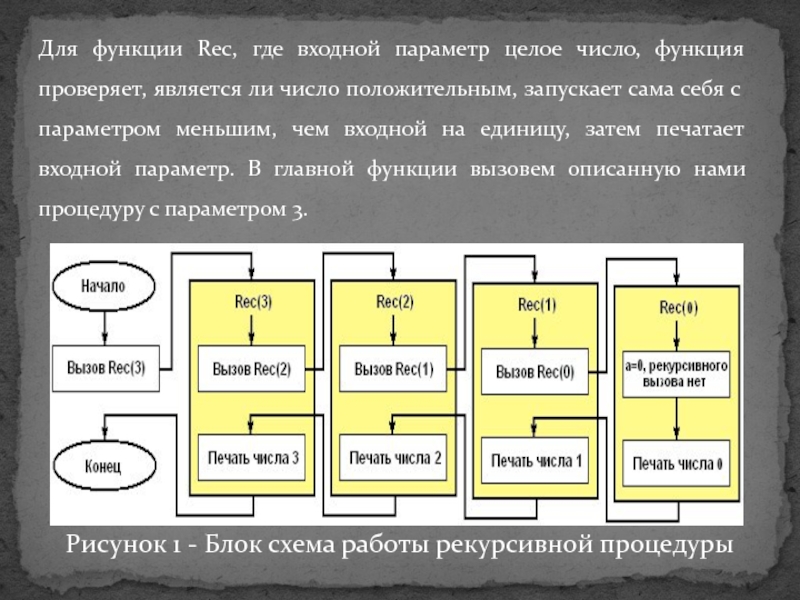
- 6. Рисунок 1 - Блок схема работы рекурсивной
- 7. Вообще нет определенного стандарта для графического показа
- 8. Рисунок 2 - Выполнение процедуры Rec с
- 9. Возможна чуть более сложная схема: функция A
- 10. Если обычную рекурсию можно уподобить уроборосу (рисунок
- 11. Рисунок 3 - Уроборос – змей, пожирающий
- 12. Рисунок 4 - Сложная рекурсия.
- 13. Теоретической базой для рекурсивных функций, вызывающих себя
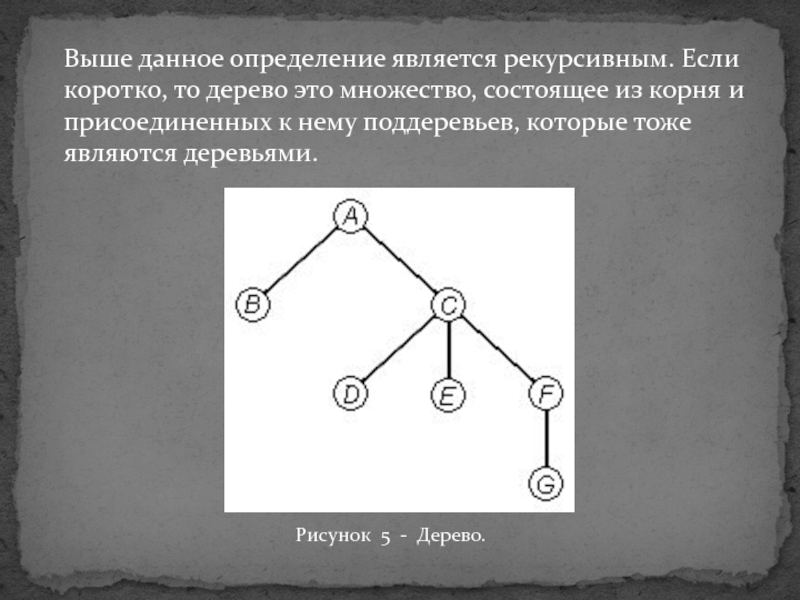
- 14. Выше данное определение является рекурсивным. Если коротко,
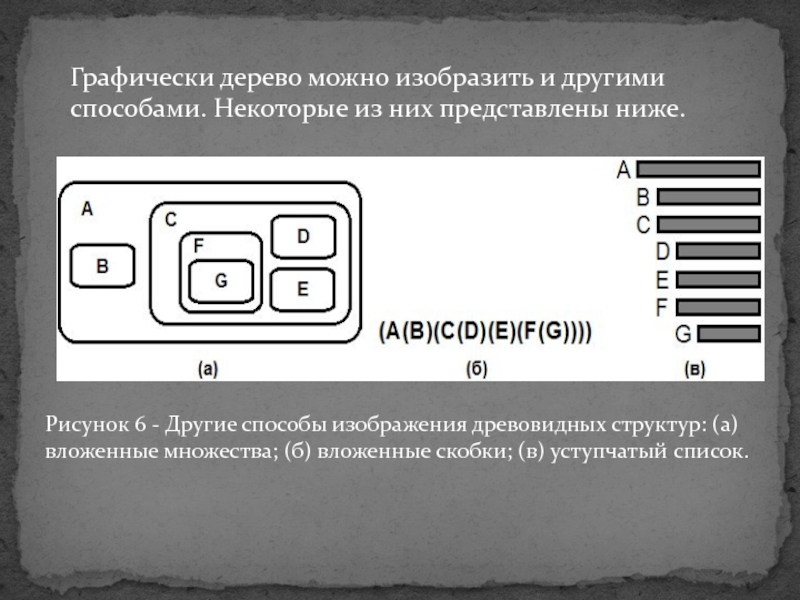
- 15. Графически дерево можно изобразить и другими способами.
- 16. Во всех алгоритмах, связанных с древовидными структурами
- 17. Алгоритм обхода в обратном порядке: Пройти левое поддерево, Попасть
- 18. Рассмотрим алгоритм рисования деревца, изображенного на рисунке
- 19. Ханойские башниСогласно легенде в Великом храме города
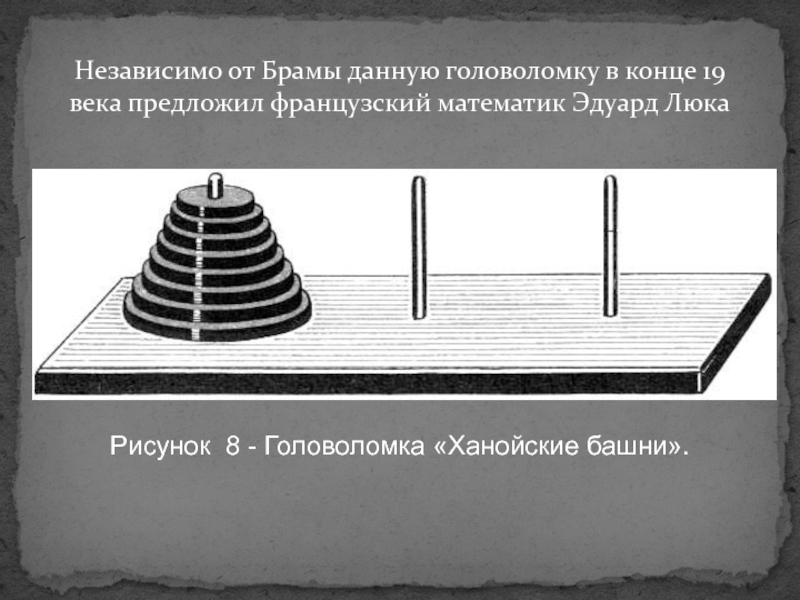
- 20. Независимо от Брамы данную головоломку в конце
- 21. Предположим, что существует решение для n-1 диска.
- 22. Фракталами называют геометрические фигуры, обладающие свойством самоподобия,
- 23. Он делится на три части, средняя часть
- 24. Такая операция повторяется с каждым из получившихся
- 25. Кривая Коха получается после бесконечного числа таких
- 26. Избавление от рекурсииЛюбой рекурсивный алгоритм может быть
- 27. Преимущество рекурсивного определения объекта заключается в том,
- 28. Рекурсияэто мощный метод программирования, который позволяет разбить
- 29. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Рекурсия — способ общего определения множества объектов или функций через себя,
с использованием ранее заданных частных определений.
выделить самоподобие задачи.Слайд 4Или как в народной песенке:
У попа была собака, он её
любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
У
попа была собака, он её любил, Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
У попа была собака, он её любил,
Она съела кусок мяса, он её убил,
В землю закопал,
Надпись написал:
…
Слайд 5В программировании рекурсия — вызов функции (процедуры) из неё же самой,
непосредственно (простая рекурсия) или через другие функции (сложная рекурсия), например,
функция A вызывает функцию B, а функция B — функцию A. Количество вложенных вызовов функции или процедуры называется глубиной рекурсии.Слайд 6Рисунок 1 - Блок схема работы рекурсивной процедуры
Для функции Rec,
где входной параметр целое число, функция проверяет, является ли число
положительным, запускает сама себя с параметром меньшим, чем входной на единицу, затем печатает входной параметр. В главной функции вызовем описанную нами процедуру с параметром 3.Слайд 7
Вообще нет определенного стандарта для графического показа рекурсии .
Еще один
визуальный образ происходящего представлен на рис. 2.
Слайд 8Рисунок 2 - Выполнение процедуры Rec с параметром 3 состоит
из выполнения процедуры Rec с параметром 2 и печати числа
3. В свою очередь выполнение процедуры Rec с параметром 2 состоит из выполнения процедуры Rec с параметром 1 и печати числа 2. И т. д.Слайд 9Возможна чуть более сложная схема: функция A вызывает функцию B,
а та в свою очередь вызывает A. Это называется сложной
рекурсией. При этом оказывается, что описываемая первой процедура должна вызывать еще не описанную. Чтобы это было возможно, требуется использовать опережающее описание.Опережающее описание процедуры B позволяет вызывать ее из процедуры A.
Слайд 10Если обычную рекурсию можно уподобить уроборосу (рисунок 3), то образ
сложной рекурсии можно почерпнуть из известного детского стихотворения, где «Волки
с перепуга, скушали друг друга». Представьте себе двух съевших друг друга волков, и вы поймете сложную рекурсию.Слайд 11Рисунок 3 - Уроборос – змей, пожирающий свой хвост. Рисунок
из алхимического трактата «Synosius» Теодора Пелеканоса (1478г).
Слайд 13Теоретической базой для рекурсивных функций, вызывающих себя более одного раза,
служит раздел дискретной математики, изучающий деревья.
Определение: Деревом будем называть конечное
множество T, состоящее из одного или более узлов, таких что:
а) Имеется один специальный узел, называемый корнем данного дерева. б) Остальные узлы (исключая корень) содержатся в попарно непересекающихся подмножествах , каждое из которых в свою очередь является деревом. Деревья называются поддеревьями данного дерева.
Слайд 14Выше данное определение является рекурсивным. Если коротко, то дерево это
множество, состоящее из корня и присоединенных к нему поддеревьев, которые
тоже являются деревьями.Рисунок 5 - Дерево.
Слайд 15Графически дерево можно изобразить и другими способами. Некоторые из них
представлены ниже.
Рисунок 6 - Другие способы изображения древовидных структур: (а)
вложенные множества; (б) вложенные скобки; (в) уступчатый список.Слайд 16Во всех алгоритмах, связанных с древовидными структурами неизменно встречается одна
и та же идея, а именно идея прохождения или обхода
дерева. Это – такой способ посещения узлов дерева, при котором каждый узел проходится точно один раз.Алгоритм обхода в прямом порядке:
Попасть в корень,
Пройти все поддеревья слева на право в прямом порядке.
Данный алгоритм рекурсивен, так как прохождение дерева содержит прохождение поддеревьев, а они в свою очередь проходятся по тому же алгоритму.
В частности для дерева на рисунках 5 и 6 прямой обход дает последовательность узлов: A, B, C, D, E, G, H.
Слайд 17Алгоритм обхода в обратном порядке:
Пройти левое поддерево,
Попасть в корень,
Пройти следующее
за левым поддерево.
Попасть в корень,
и т.д пока не будет пройдено
крайнее правое поддерево.То есть проходятся все поддеревья слева на право, а возвращение в корень располагается между этими прохождениями. Для дерева на рисунках 5 и 6 это дает последовательность узлов: B, A, D, C, E, G, F.
Слайд 18Рассмотрим алгоритм рисования деревца, изображенного на рисунке 7. Если каждую
линию считать узлом, то данное изображение вполне удовлетворяет определению дерева.
Рисунок
7 - ДеревцеРекурсивная процедура, очевидно должна рисовать одну линию (ствол до первого разветвления), а затем вызывать сама себя для рисования двух поддеревьев. Поддеревья отличаются от содержащего их дерева координатами начальной точки, углом поворота, длиной ствола и количеством содержащихся в них разветвлений (на одно меньше). Все эти отличия следует сделать параметрами рекурсивной процедуры.
Слайд 19Ханойские башни
Согласно легенде в Великом храме города Бенарас, под собором,
отмечающим середину мира, находится бронзовый диск, на котором укреплены 3
алмазных стержня, высотой в один локоть и толщиной с пчелу. Давным-давно, в самом начале времен монахи этого монастыря провинились перед богом Брамой. Разгневанный, Брама воздвиг три высоких стержня и на один из них поместил 64 диска из чистого золота, причем так, что каждый меньший диск лежит на большем. Как только все 64 диска будут переложены со стержня, на который Бог Брама сложил их при создании мира, на другой стержень, башня вместе с храмом обратятся в пыль и под громовые раскаты погибнет мир.Слайд 20Независимо от Брамы данную головоломку в конце 19 века предложил
французский математик Эдуард Люка
Рисунок 8 - Головоломка «Ханойские башни».
Слайд 21Предположим, что существует решение для n-1 диска. Тогда для перекладывания
n дисков надо действовать следующим образом:
1) Перекладываем n-1 диск.
2) Перекладываем
n-й диск на оставшийся свободным штырь.
3) Перекладываем стопку из n-1 диска, полученную в пункте (1) поверх n-го диска.Поскольку для случая n = 1 алгоритм перекладывания очевиден, то по индукции с помощью выполнения действий (1) – (3) можем переложить произвольное количество дисков.
Слайд 22Фракталами называют геометрические фигуры, обладающие свойством самоподобия, то есть состоящие
из частей, подобных всей фигуре.
Классическим примером является кривая Коха, построение
которой показано на рисунке 9. Изначально берется отрезок прямой (рисунке 9а). Рисунок 9 - Процесс построения кривой Коха
Слайд 23Он делится на три части, средняя часть изымается и вместо
нее строится угол (рисунке 9б), стороны которого равны длине изъятого
отрезка (то есть 1/3 от длины исходного отрезка ).Рисунок 9 - Процесс построения кривой Коха
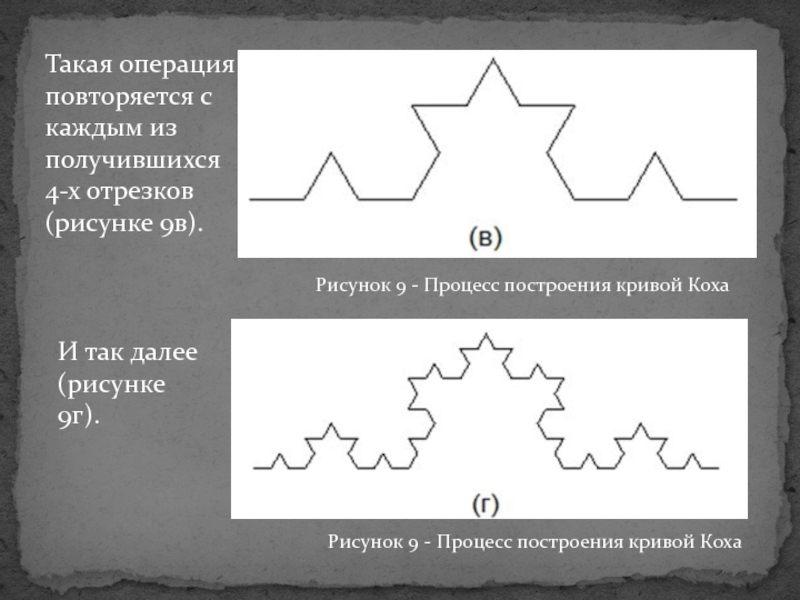
Слайд 24Такая операция повторяется с каждым из получившихся 4-х отрезков (рисунке
9в).
Рисунок 9 - Процесс построения кривой Коха
Рисунок 9 -
Процесс построения кривой КохаИ так далее (рисунке 9г).
Слайд 25Кривая Коха получается после бесконечного числа таких итераций. На практике
построение можно прекратить, когда размер деталей окажется меньше разрешения экрана
(рисунке 9д).Рисунок 9 - Процесс построения кривой Коха
Слайд 26Избавление от рекурсии
Любой рекурсивный алгоритм может быть переписан без использования
рекурсии. Заметим, что быстродействие алгоритмов при избавлении от рекурсии, как
правило, повышается. Еще одной причиной чтобы избавиться от рекурсии является ограничение на объем хранимых программой локальных переменных и значений параметров одновременно выполняющихся процедур.Так почему же люди продолжают пользоваться рекурсивными алгоритмами? Очевидно, потому что это проще и естественнее, чем соответствующие нерекурсивные решения.