Решение нелинейных уравнений

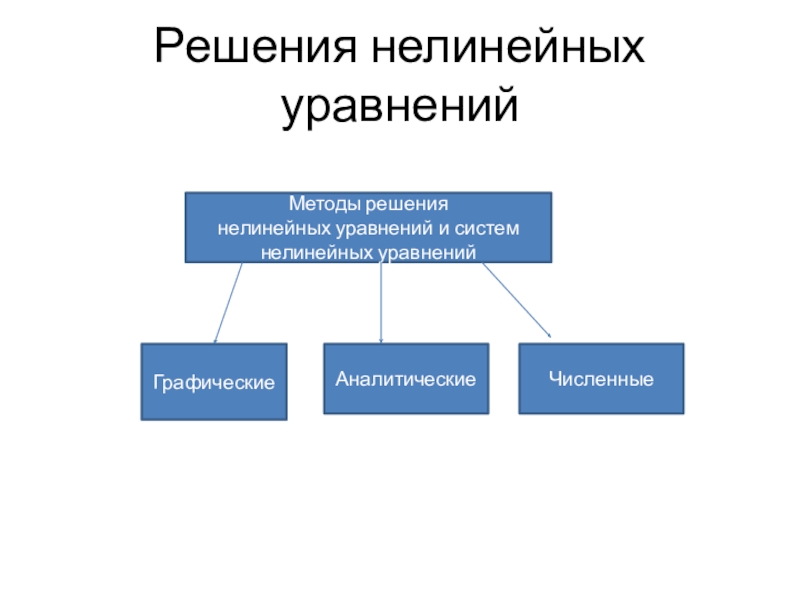
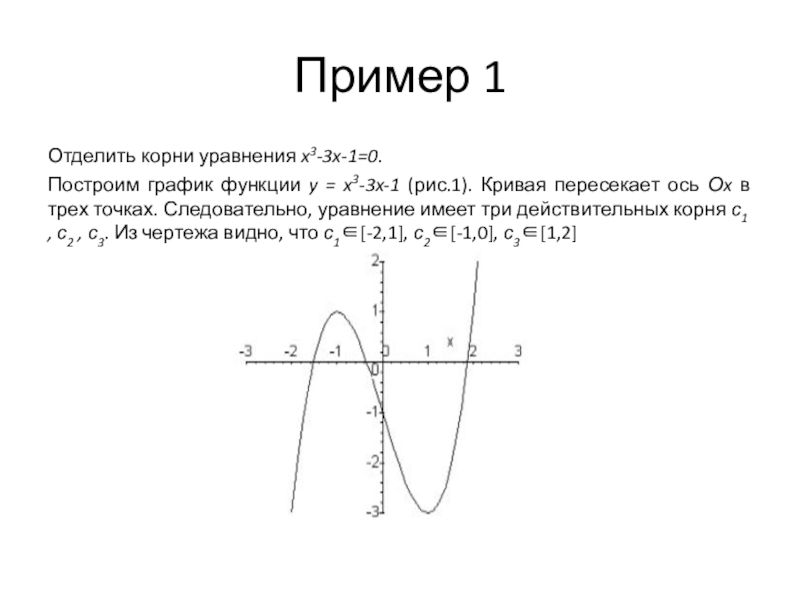
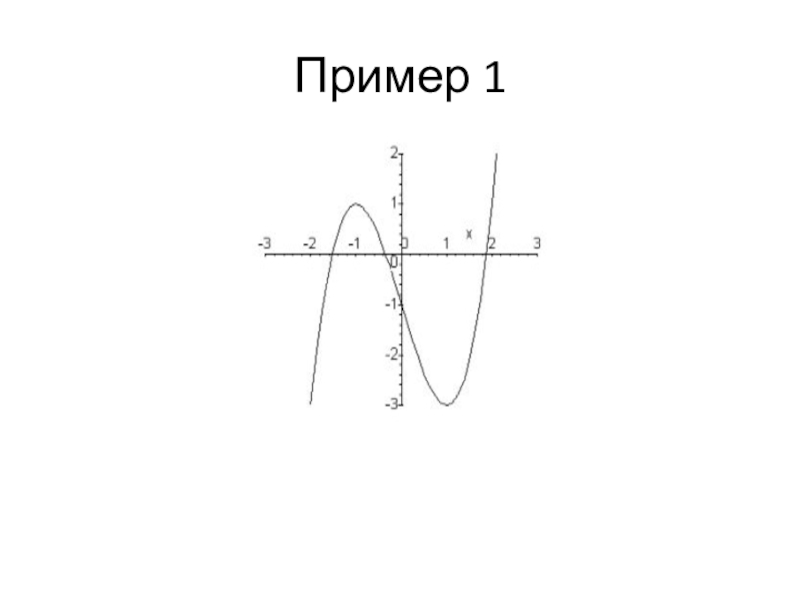
степень больше единицы, называются нелинейными.
Например, y=ax+b – линейное уравнение,

х3 – 0,2x2 + 0,5x + 1,5 = 0 – нелинейное (в общем виде записывается как F(x)=0).
Системой нелинейных уравнений считается одновременное решение нескольких нелинейных уравнений с одной или несколькими переменными.

находится одно значение корня.
В общем случае отделение корней уравнения f(x)=0

базируется на известной теореме, утверждающей, что если непрерывная функция f(x) на концах отрезка [a,b] имеет значения разных знаков, т.е. f(a)×f(b)< 0 , то в указанном промежутке содержится хотя бы один корень. Например, для уравнения f(x)=x3-6x+2=0 видим, что при х∞ f(x)>0, при х-∞ f(x)<0 что уже свидетельствует о наличии хотя бы одного корня.
Для уравнения f(x)=ex+x=0 видим, что f(∞)>0, f(-∞)<0.
Обнаружив, что устанавливаем факт наличия единственного корня, и остается лишь найти его.

Точки пересечения графика с осью 0x дают значения корней, и

по графику легко определить два числа a и b, между которыми заключен только один корень.
Построение исходной функции либо разбиение функции.

(рис.1). Кривая пересекает ось Оx в трех точках. Следовательно, уравнение

имеет три действительных корня с1 , с2 , с3. Из чертежа видно, что с1[-2,1], с2[-1,0], с3[1,2]

1. Если непрерывная функция f(x) принимает на концах отрезка [a;

b] значения разных знаков, т.е. то на этом отрезке содержится по крайней мере один корень уравнения.
Теорема 2. Если непрерывная на отрезке [a; b] функция f(x) принимает на концах отрезка значения разных знаков, а производная f'(x) сохраняет знак внутри указанного отрезка, то внутри отрезка существует единственный корень уравнения f(x) = 0.

т.к. функция f: f(x)= х5-4х2+х определена и непрерывна на всей

действительной прямой и