Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение систем линейных алгебраических уравнений
Содержание
- 1. Решение систем линейных алгебраических уравнений
- 2. РанееВозможности MATLABлевостороннее делениеx = A\bобратная матрицаx = inv(A)*b
- 3. Небольшие системы уравненийНебольшая система содержит, как привило,
- 4. Графический метод
- 5. Сложные случаи решенийТри случаяПараллельные линиинет решенияСовпадающие линиимножество
- 6. Метод Крамера
- 7. Метод Крамера
- 8. Исключение неизвестных
- 9. Исключение неизвестных
- 10. Метод Гаусса
- 11. Метод Гаусса – Прямой ход
- 12. Метод Гаусса – Прямой ход
- 13. Метод Гаусса – Прямой ход
- 14. Метод Гаусса – Прямой ход
- 15. Метод Гаусса – Обратный ход
- 16. Пример
- 17. Метод Гаусса с обратной подстановкойВ рассмотренном варианте
- 18. Пример – Частный выбор главного элемента
- 19. Пример – Частный выбор главного элемента
- 20. Пример – MATLAB
- 21. Расчет определителя матрицы
- 22. Факторизация матрицВ математике факторизация или факторинг - это
- 23. LU факторизация
- 24. LU факторизация
- 25. LU факторизацияДва основных шага решения системыфакторизациявыполняется декомпозиция
- 26. Метод Гаусса как LU факторизация
- 27. Метод Гаусса как LU факторизация
- 28. Метод Гаусса как LU факторизация
- 29. Метод Гаусса как LU факторизация
- 30. Пример - Проверка
- 31. Пример - Проверка
- 32. Метод Гаусса как LU факторизация
- 33. Пример
- 34. Пример
- 35. LU факторизация с выбором главного элементаАналогично методу
- 36. LU факторизация с выбором главного элемента
- 37. Пример
- 38. Пример
- 39. LU факторизация – MATLAB функцииlu[L,U] = lu(A)
- 40. Пример
- 41. Факторизация Холецкого
- 42. Пример
- 43. Пример
- 44. Факторизация Холецкого
- 45. Факторизация Холецкого – MATLAB функцииcholU = chol(A)
- 46. Пример
- 47. Левостороннее деление MATLABПри использовании левостороннего деления «\»
- 48. QR факторизация
- 49. QR факторизация – MATLAB функцииqr[Q,R] = qr(A)
- 50. Пример
- 51. Итерационные методыИтерационные или аппроксимационные методы являются альтернативой
- 52. Метод Гаусса-Зейделя
- 53. Метод Гаусса-Зейделя
- 54. Пример
- 55. Пример
- 56. Пример
- 57. Метод ЯкобиМетод Гаусса-Зейделя использует найденное значение х
- 58. Сходимость и диагональное преобладание
- 59. Пример
- 60. Метод релаксации
- 61. Метод релаксации
- 62. Пример
- 63. Пример
- 64. Пример
- 65. Скачать презентанцию
РанееВозможности MATLABлевостороннее делениеx = A\bобратная матрицаx = inv(A)*b
Слайды и текст этой презентации
Слайд 5Сложные случаи решений
Три случая
Параллельные линии
нет решения
Совпадающие линии
множество решений
Близкие линии
трудно определить
точку пересечения
Системы в 1 и 2 случае называются – вырожденными
(особыми, сингулярными)Случай 3 соответствует плохо обусловленной системе
существуют сложности при численном решении
Слайд 17Метод Гаусса с обратной подстановкой
В рассмотренном варианте метода Гаусса могут
возникнуть ситуации когда решение не может быть найдено или иметь
существенную погрешностьнапример, в случае если главный элемент равен 0, при нормализации возникает деление на 0
также существенно меньшее значение главного элемента по сравнению с остальными может привести к увеличению погрешности вычислений
Решение – выбор главного элемента
частный
выбор максимального значения главного элемента с последующей перестановкой строк
полный (применяется редко)
выбор максимального значения главного элемента с последующей перестановкой строк и столбцов
Слайд 22Факторизация матриц
В математике факторизация или факторинг - это декомпозиция объекта (например,
числа, полинома или матрицы) в произведение других объектов или факторов,
которые, будучи перемноженными, дают исходный объектЦелью факторизации является приведение объекта к «основным строительным блокам»
Матрица может также быть факторизована на произведение матриц специального вида для приложений, в которых эта форма удобна
Виды факторизации матриц
LU
Холецкого
QR
Слайд 25LU факторизация
Два основных шага решения системы
факторизация
выполняется декомпозиция матрицы А на
верхнюю U и нижнюю L треугольные матрицы
подстановка
прямая подстановка определяет промежуточный
вектор dобратная подстановка определяет вектор неизвестных x
факторизация
подстановка
прямая
обратная
Слайд 35LU факторизация с выбором главного элемента
Аналогично методу Гаусса для обеспечения
надежности решения при использовании LU факторизации необходимо применять частный выбор
главного элементаодним из способов является использование матрицы перестановки
единичная матрица для взаимной замены строк и столбцов
Слайд 39LU факторизация – MATLAB функции
lu
[L,U] = lu(A) – возвращает верхнюю
треугольную матрицу U и психологическую нижнюю матрицу L (то есть
произведение нижней треугольной матрицы и матрицы перестановок), так что A=L*U[L,U,P] = lu(A) – возвращает верхнюю треугольную матрицу U, нижнюю треугольную матрицу L и сопряженную (эрмитову) матрицу матрицы перестановок P, так что L*U =P*A
![LU факторизация – MATLAB функцииlu[L,U] = lu(A) – возвращает верхнюю треугольную матрицу U и психологическую нижнюю матрицу](/img/tmb/3/225709/d718dddf4b605c019c53fbd36f2af29e-800x.jpg "Решение систем линейных алгебраических уравнений LU факторизация – MATLAB функцииlu[L,U] = lu(A) – возвращает верхнюю треугольную")
Слайд 45Факторизация Холецкого – MATLAB функции
chol
U = chol(A) – для квадратной
матрицы A возвращает верхнюю треугольную матрицу U, так что U'*U=A
Разложение
Холецкого возможно для действительных и комплексных эрмитовых матриц
Слайд 47Левостороннее деление MATLAB
При использовании левостороннего деления «\» MATLAB выполняет оценку
матрицы коэффициентов и применяет оптимальный метод для решения
MATLAB проверяет вид
матрицы коэффициентов при неизвестных для возможности нахождения решения без применения полного метода Гауссаразреженная
треугольная
симметричная
В противном случае применяется для квадратной матрицы применяется метод Гаусса с частным выбором главного элемента
Слайд 49QR факторизация – MATLAB функции
qr
[Q,R] = qr(A) – вычисляет верхнюю
треугольную матрицу R того же размера, как и у A,
и унитарную матрицу Q, так что X=Q*R[Q,R,P] = qr(A) – вычисляет матрицу перестановок P, верхнюю треугольную матрицу R с убывающими по модулю диагональными элементами и унитарную матрицу Q, так что A*P=Q*R
Матрица перестановок P выбрана так, что abs(diag(R)) уменьшается
[Q,R] = qr(A,0) и [Q,R,P] = qr(A,0) – вычисляют экономное разложение, в котором P – вектор перестановок, так что Q*R=A(:,P)
Матрица P выбрана так, что abs(diag(R)) уменьшается
![QR факторизация – MATLAB функцииqr[Q,R] = qr(A) – вычисляет верхнюю треугольную матрицу R того же размера, как](/img/thumbs/22976657d08e3faeeaa5cc9561aa8d25-800x.jpg "Решение систем линейных алгебраических уравнений QR факторизация – MATLAB функцииqr[Q,R] = qr(A) – вычисляет верхнюю треугольную")
Слайд 51Итерационные методы
Итерационные или аппроксимационные методы являются альтернативой ранее рассмотренным методам
решения СЛАУ, основанным на исключении неизвестных
Можно выделить два основных этапа
выбор
начального приближенияпоследующее систематическое уточнение
Методы
Гаусса-Зейделя
Якоби
релаксации
бисопряженных градиентов
и др.
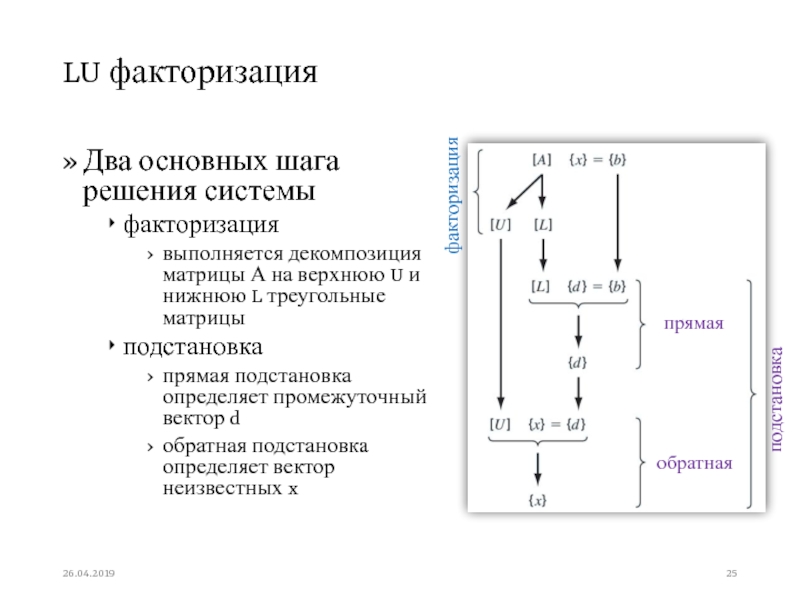
Слайд 57Метод Якоби
Метод Гаусса-Зейделя использует найденное значение х сразу же для
нахождения следующего х из другого уравнения
Несколько альтернативный подход, называемый методом
Якоби, заключается в расчете всех х на основании предыдущей итерацииГаусса-Зейдель
Якоби
