Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение задач по теме Прямолинейное равноускоренное движение
Содержание
- 1. Решение задач по теме Прямолинейное равноускоренное движение
- 2. Цели урока:Повторить основные формулы по теме «Прямолинейное равноускоренное движение».Сформировать навыки решения задач по данной теме.
- 3. Слайд 3
- 4. Задача №1. С каким ускорением движется гоночный
- 5. Задача №1. С каким ускорением движется гоночный
- 6. Задача №2 За какое время ракета приобретает
- 7. Задача №2 За какое время ракета приобретает
- 8. Задача №3 Рассчитайте длину взлетной полосы, если скорость самолета 300 км/ч, а время разгона 40 с.
- 9. Задача №3 Рассчитайте длину взлетной полосы, если
- 10. Задача №4 Скорость гоночного автомобиля в момент
- 11. Задача №4 Скорость гоночного автомобиля в момент
- 12. Задача №5 Тормозной путь автомобиля, движущегося со
- 13. Задача №5 Тормозной путь автомобиля, движущегося со
- 14. Задача №6 Какова длинна пробега самолета при
- 15. Задача №6 Какова длинна пробега самолета при
- 16. Задача №7 Автомобиль, имея начальную скорость 54
- 17. Задача №7 Автомобиль, имея начальную скорость 54
- 18. Задача №8 При равноускоренном движении с начальной
- 19. Задача №8 При равноускоренном движении с начальной
- 20. Задача №9 Два велосипедиста едут навстречу друг
- 21. Задача №9 Два велосипедиста едут навстречу друг
- 22. Задача №10 Уравнение координаты имеет вид Х
- 23. Задача №10 Уравнение координаты имеет вид Х
- 24. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Цели урока:
Повторить основные формулы по теме «Прямолинейное равноускоренное движение».
Сформировать навыки
решения задач по данной теме.
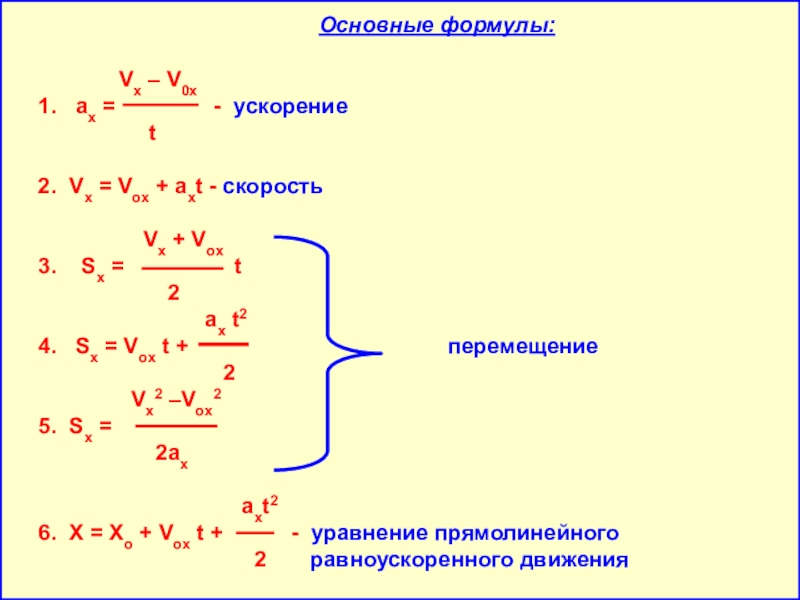
Слайд 3
Основные формулы: Vx – V0x 1. аx = - ускорение t 2. Vx = Vox + aхt - скорость Vx + Vox 3. Sx = t 2 ax t2 4. Sx = Vox t + перемещение 2 Vx2 –Vox2 5. Sx = 2ax axt2 6. X = Xo + Vox t + - уравнение прямолинейного 2 равноускоренного движения
Слайд 4Задача №1. С каким ускорением движется гоночный автомобиль, если его скорость
за 6 с увеличивается со 144 до 216 км/ч?
Слайд 5Задача №1. С каким ускорением движется гоночный автомобиль, если его скорость
за 6 с увеличивается со 144 до 216 км/ч?
Дано “СИ” Решение:Vo=144 км/ч 40 м/с V - Vo
V = 216 км/ч 60 м/с а =
t = 6 с t
(60 – 40) м/с
а - ? а = = 3,33 м/с2.
6 с
Ответ: а = 3,33 м/с2.
км 144 · 1000 м м
144 = = 40
ч 3600 с с
км 216 · 1000 м м
216 = = 60
ч 3600 с с
Слайд 6Задача №2 За какое время ракета приобретает первую космическую скорость 7,9
км/с, если она будет двигаться с ускорением 50 м/с2?
Слайд 7Задача №2 За какое время ракета приобретает первую космическую скорость 7,9
км/с, если она будет двигаться с ускорением 50 м/с2?
Дано: “СИ” Решение.V = 7,9 км/с 7900 м/с V – Vo V
Vo= 0 а = , т.к. Vo = 0, то а =
а = 50 м/с2 t t
V
t = .
a
7900 м/с
t = = 158 с.
50 м/с2
Ответ: t = 158 с.
t - ?
Слайд 8Задача №3 Рассчитайте длину взлетной полосы, если скорость самолета 300 км/ч,
а время разгона 40 с.
Слайд 9Задача №3 Рассчитайте длину взлетной полосы, если скорость самолета 300 км/ч,
а время разгона 40 с.
Дано:
“СИ” Решение.V = 300 км/ч 83,3 м/с V + Vo
Vo = 0 S = t
t = 40с 2
(83,3 + 0) м/с
S - ? S = · 40 с = 1666 м
2
Ответ: S = 1666 м ≈ 1,7 км.
Слайд 10Задача №4 Скорость гоночного автомобиля в момент начала разгона 10 м/с,
ускорение 5 м/с2. Определите путь, пройденный автомобилем за 10 с
после начала движения. Какова скорость автомобиля в конце десятой секунды разгона?Слайд 11Задача №4 Скорость гоночного автомобиля в момент начала разгона 10 м/с,
ускорение 5 м/с2. Определите путь, пройденный автомобилем за 10 с
после начала движения. Какова скорость автомобиля в конце десятой секунды разгона? Дано: Решение.
Vo= 10 м/с a t2 5 м/с2 · (10 с)2
а = 5 м/с2 S = Vot + ; S = 10 м/с · 10 с + = 350 м.
t = 10 с 2 2
S - ? V = Vo + a t ; V = 10 м/с + 5 м/с2 · 10 с = 60 м/с.
V - ?
Ответ: S = 350 м; V = 60 м/с.
Слайд 12Задача №5 Тормозной путь автомобиля, движущегося со скоростью 50 км/ч, равен
10 м. Чему равен тормозной путь этого же автомобиля при
скорости 100 км/ч?Слайд 13Задача №5 Тормозной путь автомобиля, движущегося со скоростью 50 км/ч, равен
10 м. Чему равен тормозной путь этого же автомобиля при
скорости 100 км/ч? Дано: “СИ” Решение.
V = 0 Vo12 Vo12
Vo1 = 50 км/ч 13,9 м/с S1 = a =
Vo2 = 100 км/ч 27,8 м/с 2a 2S1
S1 =10 м
Vo22 Vo22 · 2S1 Vo22
S2 = = = S1
S2 - ? 2a 2 Vo12 Vo12
(27,8 м/с)2 772,84
S2 = 10 м ----------------- = 10 ------------- = 40 м.
(13,9 м/с)2 193,21
Ответ: S2 = 40 м.
Слайд 14Задача №6 Какова длинна пробега самолета при посадке, если его посадочная
скорость 140 км/ч, а ускорение при торможении 2 м/с2?
Слайд 15Задача №6 Какова длинна пробега самолета при посадке, если его посадочная
скорость 140 км/ч, а ускорение при торможении 2 м/с2?
Дано:
“СИ” Решение.Vо = 140 км/ч 38,9 м/с V2 – Vo2
а = 2 м/с2 S = ; ax = - 2 м/с2.
V = 0 2 ax
S - ? Vo2
S =
2а
км 140 · 1000 м м
140 = = 38,9 (38,9 м/с)2
ч 3600 с с S = ≈ 378 м.
2 · 2 м/с2
Ответ: S = 378 м.
Слайд 16Задача №7 Автомобиль, имея начальную скорость 54 км/ч, при торможении по
сухой дороге проходит 30 м, а по мокрой – 90
м. Определите для каждого случая ускорение и время торможения.Слайд 17Задача №7 Автомобиль, имея начальную скорость 54 км/ч, при торможении по
сухой дороге проходит 30 м, а по мокрой – 90
м. Определите для каждого случая ускорение и время торможения. Дано: “СИ” Решение.
V = 0 V + Vo Vot 2 S
Vo = 54 км/ч 15 м/с S = t S = t = .
S1 = 30 м 2 2 Vo
S2 = 90 м
t1 = ? t2 = ?
а - ?
t - ? Vo2 Vo2
S = a = .
2 a 2 S
a1 = ? a2 = ?
Ответ: a1 = 3,75 м/с2; t1 = 4 с;
a2 = 1,25 м/с2; t1 = 12 с.
Слайд 18Задача №8 При равноускоренном движении с начальной скоростью 5 м/с тело
за 3 с прошло 20 м. С каким ускорением двигалось
тело? Какова его скорость в конце третьей секунды?Слайд 19Задача №8 При равноускоренном движении с начальной скоростью 5 м/с тело
за 3 с прошло 20 м. С каким ускорением двигалось
тело? Какова его скорость в конце третьей секунды? Дано: Решение.
Vо = 5м/с a t2 a t2 2(S – Vot)
t = 3 c S = Vot + = S – Vot a = .
S = 20 м 2 2 t2
V = Vо + at .
a - ?
V - ? 2 · (20 м – 5 м/с · 3с)
a = ≈ 1,1 м/с2;
9 с2
V = 5 м/с + 1,1 м/с2 · 3 с = 8,3 м/с.
Ответ: а = 1,1 м/с2; V = 8,3 м/с.
Слайд 20Задача №9 Два велосипедиста едут навстречу друг другу. Первый, имея начальную
скорость 9 км/ч, спускается с горы с ускорением 0,4 м/с2.
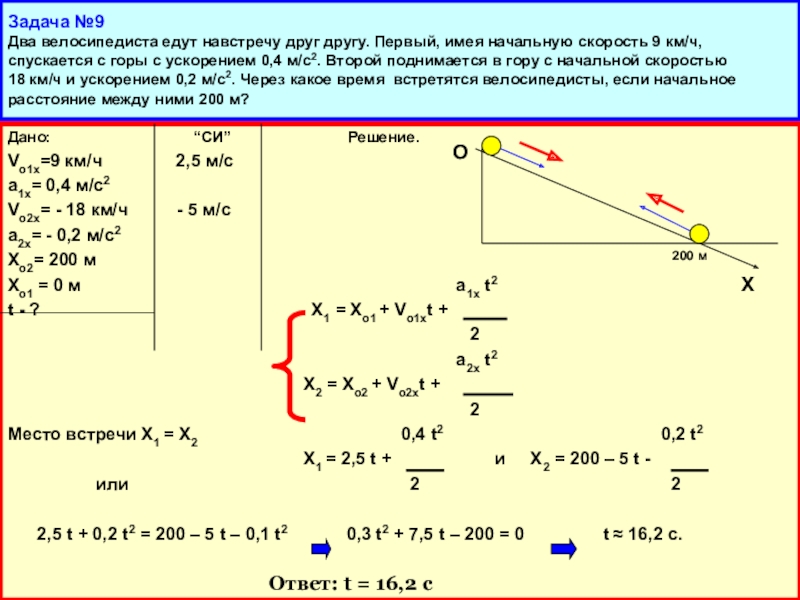
Второй поднимается в гору с начальной скоростью 18 км/ч и ускорением 0,2 м/с2. Через какое время встретятся велосипедисты, если начальное расстояние между ними 200 м?Слайд 21Задача №9 Два велосипедиста едут навстречу друг другу. Первый, имея начальную
скорость 9 км/ч, спускается с горы с ускорением 0,4 м/с2.
Второй поднимается в гору с начальной скоростью 18 км/ч и ускорением 0,2 м/с2. Через какое время встретятся велосипедисты, если начальное расстояние между ними 200 м?Дано: “СИ” Решение.
Vo1x=9 км/ч 2,5 м/с
а1х= 0,4 м/с2
Vo2x= - 18 км/ч - 5 м/с
а2х= - 0,2 м/с2
Хо2= 200 м
Хо1 = 0 м а1х t2
t - ? Х1 = Хо1 + Vo1xt +
2
а2х t2
Х2 = Хо2 + Vo2xt +
2
Место встречи Х1 = Х2 0,4 t2 0,2 t2
Х1 = 2,5 t + и X2 = 200 – 5 t -
или 2 2
2,5 t + 0,2 t2 = 200 – 5 t – 0,1 t2 0,3 t2 + 7,5 t – 200 = 0 t ≈ 16,2 c.
200 м
Х
О
Ответ: t = 16,2 c
Слайд 22Задача №10 Уравнение координаты имеет вид Х = 4 + 1,5t
+ t2. Какое это движение? Напишите формулу зависимости скорости тела
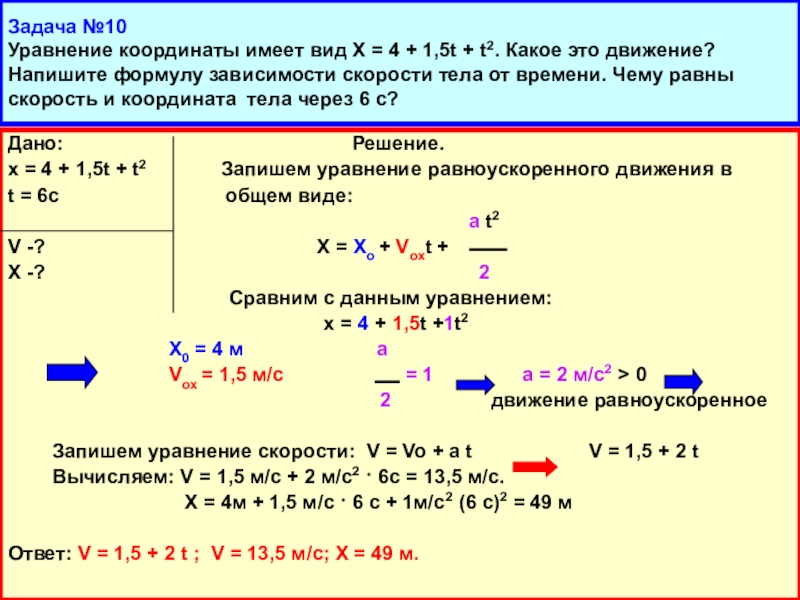
от времени. Чему равны скорость и координата тела через 6 с?Слайд 23Задача №10 Уравнение координаты имеет вид Х = 4 + 1,5t
+ t2. Какое это движение? Напишите формулу зависимости скорости тела
от времени. Чему равны скорость и координата тела через 6 с?Дано: Решение.
х = 4 + 1,5t + t2 Запишем уравнение равноускоренного движения в
t = 6c общем виде:
а t2
V -? Х = Хо + Voxt +
X -? 2
Сравним с данным уравнением:
х = 4 + 1,5t +1t2
Х0 = 4 м а
Vox = 1,5 м/с = 1 а = 2 м/с2 > 0
2 движение равноускоренное
Запишем уравнение скорости: V = Vo + a t V = 1,5 + 2 t
Вычисляем: V = 1,5 м/с + 2 м/с2 · 6с = 13,5 м/с.
Х = 4м + 1,5 м/с · 6 с + 1м/с2 (6 с)2 = 49 м
Ответ: V = 1,5 + 2 t ; V = 13,5 м/с; Х = 49 м.