Слайд 1Самостоятельная работа
1В. 1. Ребята посещают три кружка: математики, физики и
химии. Решено было организовать кружок юных техников и пригласить тех
ребят, которые не занимаются ни в одном из трех перечисленных. Сколько таких ребят, если всего в классе 36 человек, занимаются математикой- 18, физикой – 14, химией – 10; 2 посещают все три кружка, 8 – математику и физику, 5 – математику и химию, 3 – химию и физику.
2. Из 220 школьников 16 играют в баскетбол, 175 в футбол, 24 не играют в эти игры. Сколько человек одновременно играет в баскетбол, и в футбол?
2В. 1. В детском саду 11 деток любят манную кашу, 13 - гречневую, 7 – перловую, 4 – манную и гречневую, 3 – манную и перловую, 6 – гречневую и перловую, 2 – уплетают все три вида. Сколько детей в группе, если в ней нет ни одного, кто не любит кашу?
2. В классе 35 учеников. 20 из них занимаются в математическом кружке, 11 — в биологическом,
а 1- ничем не занимается. Сколько ребят занимаются и математикой, и биологией?
Слайд 21. Ребята посещают три кружка: математики, физики и химии. Решено
было организовать кружок юных техников и пригласить тех ребят, которые
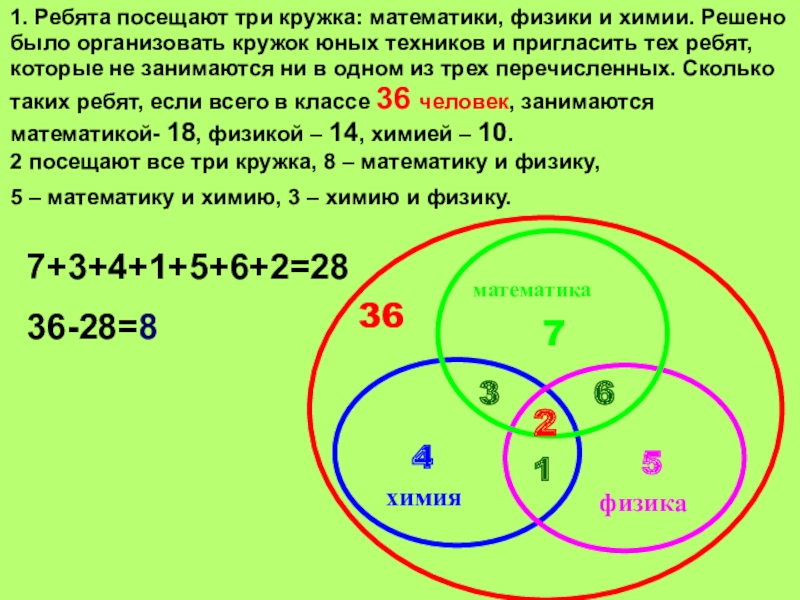
не занимаются ни в одном из трех перечисленных. Сколько таких ребят, если всего в классе 36 человек, занимаются математикой- 18, физикой – 14, химией – 10.
2 посещают все три кружка, 8 – математику и физику,
5 – математику и химию, 3 – химию и физику.
7+3+4+1+5+6+2=28
36-28=8
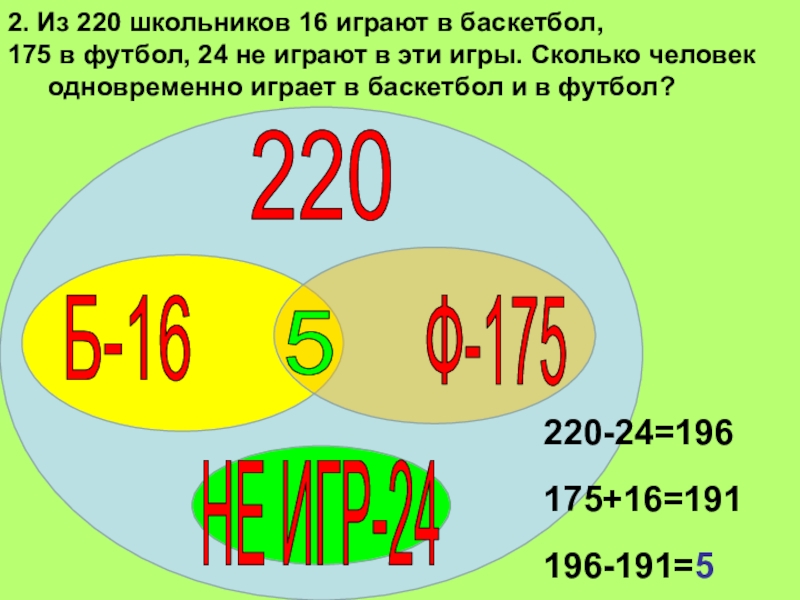
Слайд 32. Из 220 школьников 16 играют в баскетбол,
175 в
футбол, 24 не играют в эти игры. Сколько человек одновременно
играет в баскетбол и в футбол?
Б-16
Ф-175
НЕ ИГР-24
220
220-24=196
175+16=191
196-191=5
5
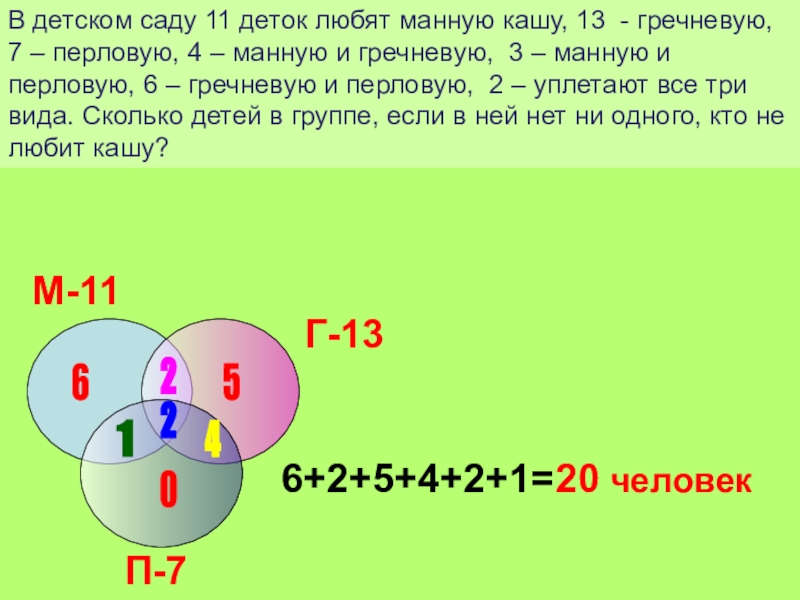
Слайд 4В детском саду 11 деток любят манную кашу, 13 -
гречневую, 7 – перловую, 4 – манную и гречневую, 3
– манную и перловую, 6 – гречневую и перловую, 2 – уплетают все три вида. Сколько детей в группе, если в ней нет ни одного, кто не любит кашу?
М-11
Г-13
П-7
2
4
2
1
6
5
0
6+2+5+4+2+1=20 человек
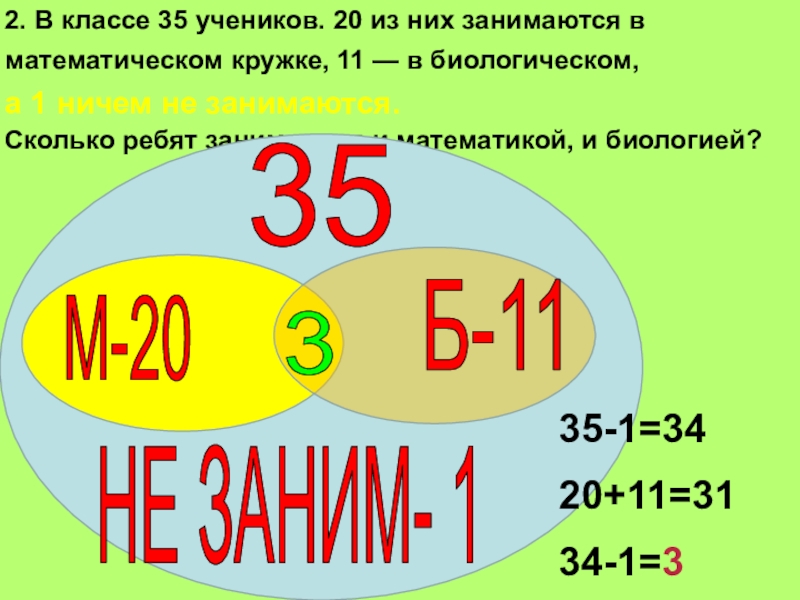
Слайд 52. В классе 35 учеников. 20 из них занимаются в
математическом кружке, 11 — в биологическом,
а 1 ничем не занимаются.
Сколько ребят занимаются и математикой, и биологией?
35
М-20
Б-11
НЕ ЗАНИМ- 1
3
35-1=34
20+11=31
34-1=3
Слайд 6Вопросы для семинара «История возникновения геометрии»
Геометрия во времена палеолита и
неолита
Геометрия в Древнем Египте
Геометрия в Древней Индии
Геометрия в Древнем Китае
Геометрия
в Древней Греции
Фалес Милетский — философ и математик ионийской философской школы
Геометрия Демокрита
Пифагор- основатель пифагорейской школы
Евклид- основатель александрийской школы
Н.И. Лобачевский - создатель неевклидовой геометрии.
Форма представления различная: презентация, сообщения. Желательно, чтобы в выступлениях были интересные факты
Слайд 8 Слово «геометрия» - греческое, оно составлено из двух частей
«гео»
и «метрия» и дословно на русский язык переводится как
«земле-мерие».
«Геометрия
– это наука о свойствах геометрических фигур»
Муза геометрии
(Лувр)
Слайд 9Геометрия приближает разум к истине.
(Платон)
Создать буклет по теме: Геометрические понятия,
изучаемые в курсе математики начальной школы (детского сада)
Слайд 10Необходимость возникновения науки
Геометрия возникла в результате
практической деятельности людей: нужно
было сооружать жилища, храмы, проводить
дороги, оросительные каналы,
устанавливать границы земельных
участков
и определять их размеры.
Важную роль играли и эстетические
потребности людей: желание украсить свои
жилища и одежду, рисовать картины
окружающей жизни.
Слайд 11Сами того не зная, люди все время занимались геометрией
Слайд 12Издавна люди любили украшать себя, свою одежду, свое жилище.
Слайд 13«Все боится времени, но само время боится пирамид».
Слайд 14Геометрия во времена палеолита и неолита
Первоначальные представления
о геометрических формах относятся к эпохе древнего каменного века –
палеолита и неолита.
В эпоху позднего палеолита люди стали украшать свои жилища наскальными рисунками и статуэтками, имевшими ритуальное значение.
С наступлением неолита произошел переход от простого собирания пищи к её производству.
В эпоху позднего неолита люди научились плавить медь и бронзу, изготовлять орудия производства и оружие.
Слайд 15Геометрия в Древнем Египте
«Геометрия была открыта египтянами
и возникла при измерении земли вследствие разливов Нила, постоянно смывающего
границы участков. Нет ничего удивительного, что эта наука, как и другие, возникла из практических потребностей человека. Всякое возникающее знание из несовершенного состояния переходит в совершенное».
древнегреческий ученый Евдем Родосский.
Слайд 16Геродот
О зарождении геометрии в Древнем Египте пишет следующее:
"Сезоострис,
египетский фараон, разделив землю, дав каждому египтянину участок по жребию
и взимал соответствующим образом налог с каждого участка.
Случалось, что Нил заливал тот или иной участок, тогда пострадавший обращался к царю, а царь посылал землемеров, чтобы установить, на сколько уменьшился участок, и соответствующим образом уменьшить налог.
Так возникла геометрия в Египте, а оттуда перешла в Грецию".
Слайд 17Геометрия в Древней Индии
имела практический характер и была тесно
связана как с повседневными потребностями, так и с религиозными обрядами,
в частности с культом жертвоприношения.
« Сульва- сутра» ( священные древнеиндийские книги) излагаются свойства фигур, связанных с построением алтарей-жертвенников.
Слайд 18Геометрия в Древнем Китае
Самое древнее китайское математико-астрономическое сочинение «Чжоу-би», написанное
около 1100 г. до н.э. в первой главе содержит предложение,
относящееся к прямоугольному треугольнику, среди которых – теорема Пифагора.
Слайд 19 Геометрия в Древней Греции
Греческие купцы познакомились
с восточной математикой, прокладывая торговые пути.
Они задавались
вопросами:
почему в равнобедренном треугольнике два угла при основании равны;
почему площадь треугольника равна половине площади прямоугольника при одинаковых основаниях и высотах?
Слайд 20Начиная с VII века до н.э. в Древней Греции
создаются философские
школы, в которых происходит постепенный переход от практической к теоретической
геометрии.
Всё больше значение в этих школах приобретают рассуждения, при помощи которых удаётся получать новые геометрические свойства, исходя из некоторых положений, принимаемых без доказательств и названных аксиомами. В переводе с греческого слово аксиома означает "принятие положения".
Разрозненные геометрические сведения, позаимствованные у египтян и у вавилонян, ученые древней Греции дополняли, уточняли, обобщали и развивали.
Слайд 21Ионийская школа Фалеса Милетского VI в. до н.э
Предложил способ определения
расстояния до корабля на море.
Вычислил высоту египетской пирамиды Хеопса по
длине отбрасываемой тени.
Доказал равенство углов при основании равнобедренного треугольника.
Создал теорему о равных отрезках, отсекаемых параллельными прямыми на сторонах угла.
У него могут поучиться краткости. Полное собрание его сочинений по преданию составляло 200 стихов.
В настоящее время существует мнение о том, что многие открытия Фалеса были просто заимствованы из египетской науки.
Слайд 22Фалес
Именно с Фалеса начинается постепенное преобразование эмпирической
египетской и вавилонской математики в греческую дедуктивную математику. По словам
Плутарха, «Фалес был в то время единственным ученым, который в своих исследованиях пошел дальше того, что нужно было для практических потребностей, все остальные получили звание ученых за свое искусство в государственных делах».
Фалес Милетский (ок. 625 — ок. 547 г. до н. э.) — философ, математик, астроном, первый из Семи мудрецов; родоначальник античной философии и науки, основатель Милетской школы; первый математик и физик в Ионии, основатель геометрии, военный инженер лидийских царей.
Слайд 23Пифагорейская школа
(VI–V вв. до н.э.)
они приписывали атомам форму правильных
многогранников: атомам огня- форму тетраэдра (4), земли - гексаэдра (куба,
6), воздуха – октаэдра (8), воды- икосаэдра(20). Всей Вселенной приписывалась форма додекаэдра (12).
«теорема Пифагора» была известна задолго до него.
рассматривали линии как следы движущихся точек, а поверхности - как следы движущихся линий.
Слайд 24Пифагор
Пифагорейцы подчеркивали реальность изменений и стремились найти
в природе и обществе неизменное. Для этого они изучали геометрию,
арифметику, астрономию и музыку – так называемый «квадривиум».
Пифагор Самосский (ок. 580 — ок. 500 до н. э.) — древнегреческий философ, религиозный и политический деятель, основатель пифагореизма, математик. Пифагору приписывается изучение свойств целых чисел и пропорций, доказательство теоремы Пифагора и др.
Слайд 25решили три великие задачи древнегреческой математики: удвоение куба, деление угла
на три равные части и квадратура круга.
используя циркуль и линейку,
выполнили построение
Слайд 26Демокрит
Как и Фалес, свои первоначальные знания Демокрит
почерпнул на Востоке: «Никто не превзошел меня в построении фигур
из линий, сопровождающихся доказательством, даже арпадонапты в Египте».
Свою геометрию Демокрит строил на основе атомистической структуры пространства: линии, поверхности, объемы считались им состоящими из большого числа конечных и далее неделимых элементов.
(Demokritos) из Абдеры во Фракии (ок. 470 или 460 — 360-е гг. до н.э.) — др.-греч. философ, основоположник атомистического учения. Автор более 70 сочинений по этике, физике, математике, языку и литературе, различным прикладным наукам, в т.ч. медицине, от которых сохранились лишь фрагменты.
Слайд 27разработали теории параллельных линий,
теорему о сумме углов треугольника, четырехугольника,
и правильных многоугольников.
исследовали окружность, правильные многогранники и шар,
открыли
правильный пятиугольник
доказали, что плоскость может быть покрыта равносторонними треугольниками, квадратами и шестиугольниками.
Слайд 28Школа Платона
(5-6 вв. до н. э.)
Платон не был математиком
и не получил никаких результатов в этой науке, но в
своих произведениях любил говорить о математике: в трактате "Таимей" изложил ученья о 5 правильных многогранниках, впоследствии получили название "платоновых тел".
Все утверждения (теоремы) должны строго логически выводиться из небольшого числа основных положений — аксиом. Такая постановка — крупнейший шаг вперёд.
Слайд 30Александрийская
школа
В 13 книгах «Начала» Евклида впервые было представлено аксиоматическое
построение геометрии. На протяжении около двух тысячелетий этот труд остается
основой изучения систематического курса геометрии.
Царь Птолемей спросил у Евклида, нельзя ли найти более короткий и менее утомительный путь к изучению геометрии, чем его "Начала". Евклид на это ответил: "В геометрии нет царского пути".
Геометрия впервые предстала как математическая наука.
Слайд 31Первая страница «Начал» Евклида. Издание 1482г.
Слайд 32Одна из страниц «Начал» Евклида. Издание 1482г.
Слайд 33 Первые четыре книги посвящены геометрии на плоскости.
В
1 книге излагается планиметрия прямолинейных фигур: устанавливаются их свойства, заканчивается
прямой и обратной теоремой Пифагора.
Во 2 книге излагается основы геометрической алгебры.
3-я книга посвящена свойствам круга, в четвертой строятся правильные п-угольники при п = 3, 4, 5, 6, 10...
11 книга посвящена стереометрии. Она содержит основные теоремы о прямых и плоскостях в трехмерном пространстве, задачи на построение, например, как опустить перпендикуляр из данной точки на данную плоскость.
12 книга посвящена решению задачи о квадратуре круга.
13 книга излагает учение о правильных многогранниках.
В целом творение Евклида величественно.
Созданная им система просуществовала более двух тысяч лет.
Слайд 34В книге 35 определений:
Точка есть то , что не имеет
частей
Линия есть длина без ширины
Прямая линия есть та, которая одинаково
лежит относительно всех своих точек
Поверхность есть то , что имеет длину и ширину
5 постулатов
От каждой точки до каждой другой точки можно провести прямую
Ограниченную прямую можно продолжить неопределенно
Из любого центра можно описать окружность любым радиусом
Все прямые углы равны…
Аксиомы (5)
Теоремы
Задачи на построение
Слайд 35Архимед
Архимед - один из немногих учёных
античности, которого мы знаем не только по имени. Он был
уникальным учёным - механиком, физиком, математиком.
Архимед, по выражению современников, был околдован геометрией, и, хотя у него было много прекрасных открытий, он просил на своей могиле изобразить цилиндр со вписанным в него шаром и указать соотношение объёмов этих тел. Позже именно по этому изображению была найдена могила Архимеда.
Архимед (около 287 до н.э., Сиракузы, Сицилия — 212 до н.э., там же) — древнегреческий ученый, математик и механик, основоположник теоретической механики и гидростатики. Разработал предвосхитившие интегральное исчисление методы нахождения площадей, поверхностей и объемов различных фигур и тел.
Слайд 36Существенный вклад внес выдающийся ученый Архимед (287 – 212гг. до
н. э.): теоремы о площадях плоскостных фигур, объемах тел; работы
«Измерение круга», «О шаре и цилиндре», «О многогранниках».
Впервые открыл равноугольно полуправильные многогранники. Им подробно описаны 13 многогранников, которые позже в честь великого учёного были названы телами Архимеда.
Слайд 38Существуют правильные звездчатые многогранники. Их всего четыре, они называются также
телами Кеплера-Пуансо.
Слайд 39 Н.И. Лобачевский
В 1826 году великий русский
математик поставил точку в проблеме пятого постулата.
Дальнейшие его рассуждения
привели его к новой безупречной геометрической системе, называемой сейчас геометрией Лобачевского (неевклидова геометрия).
Многие русские ученые не понимали
Лобачевского.
Слайд 40 Французский математик и философ.
В труде «Геометрия» заложил основы
аналитической геометрии, создав метод координат и применил алгебраическую символику в
геометрии.
Архимед
Евклид
Пифагор
Фалес
К.Ф.Гаусс
Н.И.Лобачевский
Декарт Р.
Ф.Виет
1 вопрос
Слайд 412 вопрос
Древнегреческий математик.
В его главной работе «Начало» подведен
итог предшествующему развитию греческой математики.
Он ввел понятие иррационального числа,
показал бесконечность множества простых чисел, изложил аксиоматический способ построения геометрии, которая сейчас изучается в школе.
Архимед
Евклид
Пифагор
Фалес
К.Ф.Гаусс
Н.И.Лобачевский
Декарт Р.
Ф.Виет
Слайд 423 вопрос
Русский математик.
Создатель неевклидовой геометрии.
Архимед
Евклид
Пифагор
Фалес
К.Ф.Гаусс
Н.И.Лобачевский
Декарт Р.
Ф.Виет
Слайд 434 вопрос
Древнегреческий ученый, доказавший знаменитую теорему о прямоугольном треугольнике, первый
высказал предположение о том, что Земля вращается вокруг Солнца.
Архимед
Евклид
Пифагор
Фалес
К.Ф.Гаусс
Н.И.Лобачевский
Декарт Р.
Ф.Виет
Слайд 445 вопрос
Древнегреческий ученый, который доказал, что если параллельные прямые пересекающие
стороны отсекают на одной его стороне равные отрезки, то они
отсекают равные отрезки и на другой его стороне.
Архимед
Евклид
Пифагор
Фалес
К.Ф.Гаусс
Н.И.Лобачевский
Декарт Р.
Ф.Виет
Слайд 456 вопрос
Древнегреческий ученый.
Однажды выскочил на улицу с криком «Эврика».
В этот момент он открыл важнейший закон физики.
Он также
нашел приближенное значение числа в виде обыкновенной дроби.
Архимед
Евклид
Пифагор
Фалес
К.Ф.Гаусс
Н.И.Лобачевский
Декарт Р.
Ф.Виет
Слайд 46 Oснователь милетской школы, один из легендарных "семи мудрецов". Происходил из
аристократического рода, был связан с храмом Аполлона Дидимского, патрона морской
колонизации. Имя Фалеса уже в V в. стало нарицательным для мудреца. Считается, что Фалес ввел в употребление новое созвездие - Малую Медведицу.
Фалеса называют одним из первых греческих мыслителей, кто понял важность астрологии как науки. В историю вошло "затмение Фалеса " 28 мая 585 г. до н.э., предсказанное им за 6 лет до события (некоторые ученые считают это легендой, доказывая, что уровень развития науки во времена Фалеса еще не позволял предсказывать затмения). В честь Фалеса названа малая планета 6001 Thales.
Фалес Милетский
(639 – 548 гг. до н. э.)
Слайд 47Гиппократ из Хиоса
Первый систематический курс планиметрии принадлежит
ионийскому философу и математику Гиппократу из Хиоса. В этом сочинении
Гиппократа уже в полном объеме применяется принцип логического заключения от одного утверждения к другому. «Начала» Гиппократа включали в себя теорию параллельных, сумму углов треугольника, площади многоугольника и вычисление площади круга.
Гиппократ из Хиоса (440 до н. э.), древнегреческий математик и астроном. В молодости он занимался торговлей, но не преуспел в ней. Разорившись, Гиппократ приехал в Афины, где вскоре стал прославленным математиком. Основная научная заслуга Гиппократа — составление первого полного свода геометрических знаний.
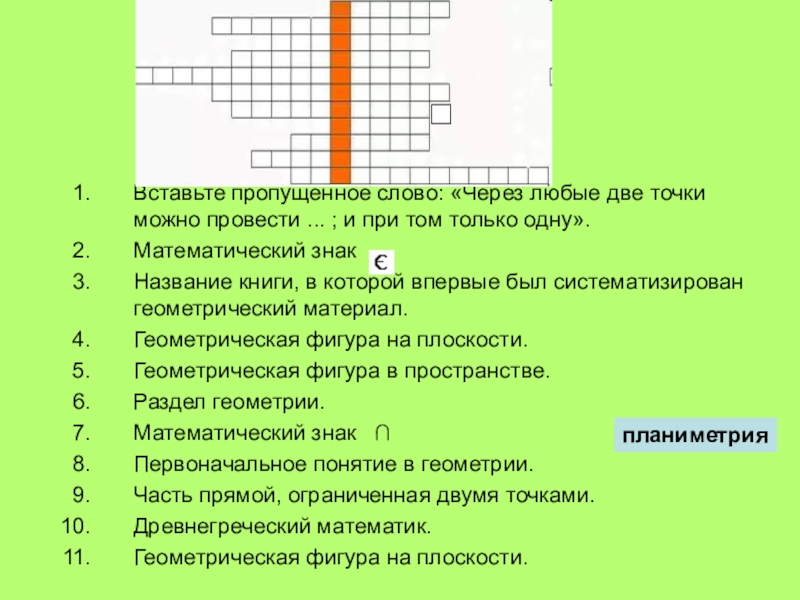
Слайд 48Вставьте пропущенное слово: «Через любые две точки можно провести ...
; и при том только одну».
Математический знак
Название книги, в
которой впервые был систематизирован геометрический материал.
Геометрическая фигура на плоскости.
Геометрическая фигура в пространстве.
Раздел геометрии.
Математический знак ∩
Первоначальное понятие в геометрии.
Часть прямой, ограниченная двумя точками.
Древнегреческий математик.
Геометрическая фигура на плоскости.
планиметрия
Слайд 49Ответы
Прямая
Принадлежит
Начала
Окружность
Параллелепипед
Стереометрия
Пересечение
Точка
Отрезок
Евклид
Прямоугольник