Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Сіденко Володимир Павлович, Старший викладач кафедри “Безпека інформаційних та
Содержание
- 1. Сіденко Володимир Павлович, Старший викладач кафедри “Безпека інформаційних та
- 2. Тема № 2КЛАСИЧНІ КРИПТОГРАФІЧНІ СИСТЕМИ З ШИФРАМИ ПЕРЕСТАНОВКИ2
- 3. Лекція № 4КЛАСИЧНІ КРИПТОГРАФІЧНІ СИСТЕМИ З ШИФРАМИ ПЕРЕСТАНОВКИ3
- 4. Питання лекції № 5 1. Криптографічні системи, які
- 5. 1. КРИПТОГРАФИЧНІ СИСТЕМИ, ЯКІ ВИКОРИСТОВУЮТЬ ШИФРИ ПРОСТОЇ ПЕРЕСТАНОВКИ5
- 6. При використанні для шифрування ін- фомації методів
- 7. 1.1. Одноразові шифри простої перестановки 7
- 8. Проста перестановка без ключа - один з
- 9. Рис. 4.1. Заповнення таблиці з 5 рядківі 7 стовпців9
- 10. Після того, як відкритий текст запи- саний
- 11. Об'єднання букв у групи не входить у
- 12. Використовуємо у вигляді ключа сло-во ЛУНАТИК, а
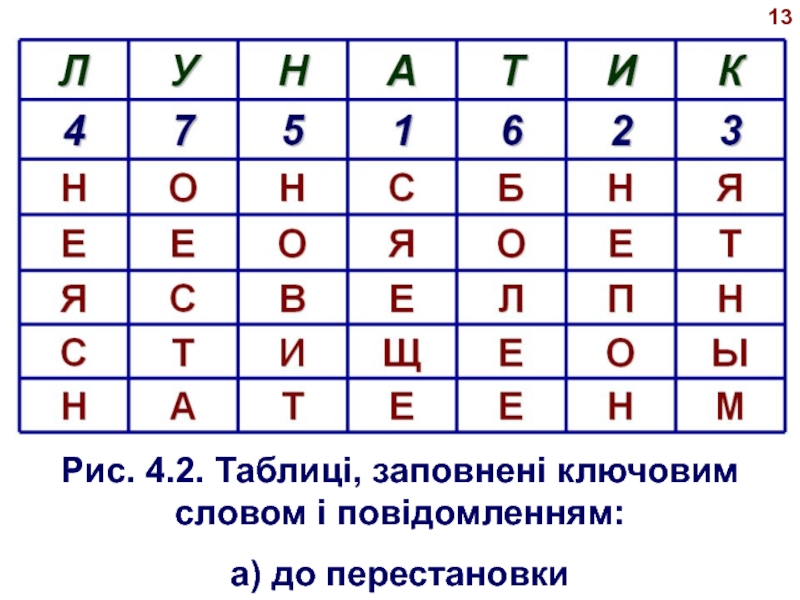
- 13. Рис. 4.2. Таблиці, заповнені ключовим словом і повідомленням:а) до перестановки 13
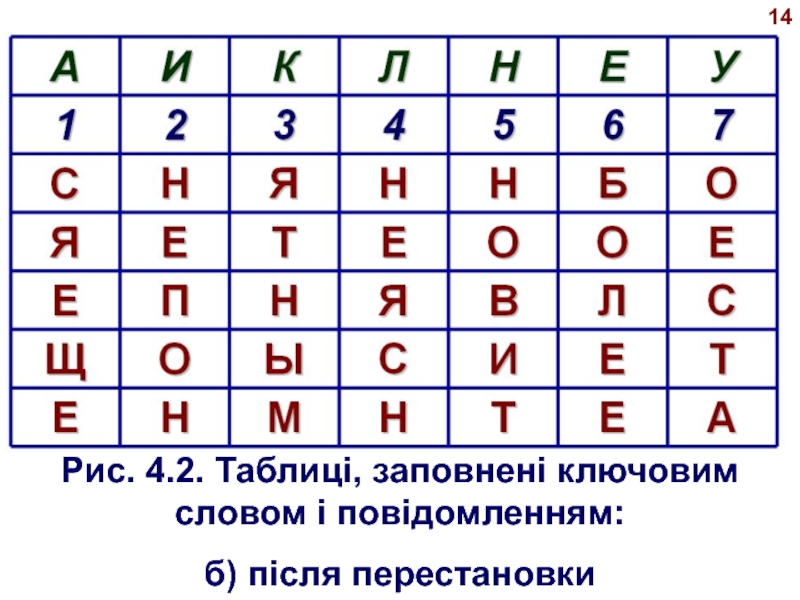
- 14. Рис. 4.2. Таблиці, заповнені ключовим словом і повідомленням:б) після перестановки14
- 15. У верхньому рядку таблиці на рис. 4.2,а
- 16. 16 При шифруванні методом простої замі- ни можна
- 17. 17Рис. 4.3. Таблиці, заповнені ключовим словом і повідомленням:а) до перестановки
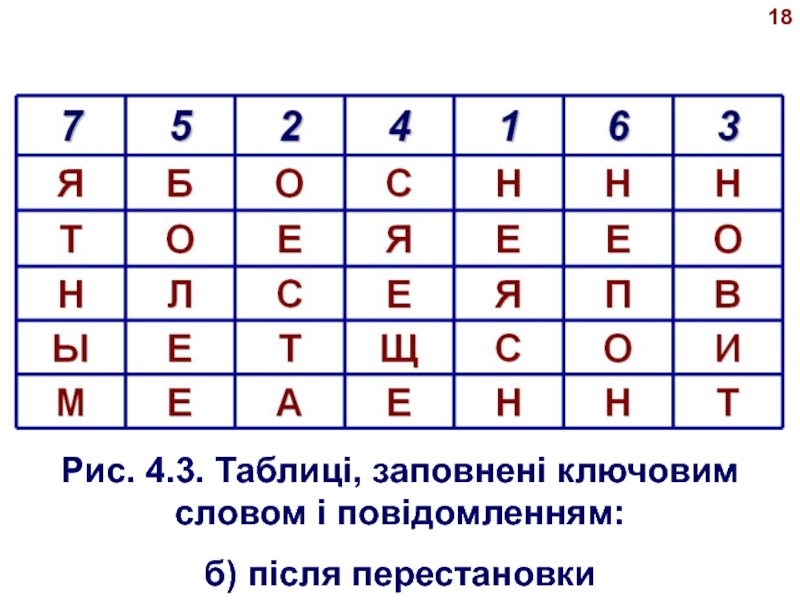
- 18. 18Рис. 4.3. Таблиці, заповнені ключовим словом і повідомленням:б) після перестановки
- 19. 19 У верхньому рядку таблиці на рис. 4.3,а
- 20. 1.2. Дворазові шифри простої перестановки20
- 21. Крім одиночних перестановок по стовпчиках використовувалися ще
- 22. 22
- 23. Нехай ключем до шифру подвійної пе- рестановки
- 24. При розшифровці порядок перестано- вок буде зворотний.
- 25. 25
- 26. Зчитуючи символи з таблиці рис. 4.5,в з
- 27. Для додаткової скритності можна пов- торно шифрувати
- 28. Такі способи заповнення таблиці якщо й не
- 29. Якщо проаналізувати шифротексти при використанні поодиноких та
- 30. 2. КРИПТОГРАФИЧНІ СИСТЕМИ, ЯКІ ВИКОРИСТОВУЮТЬ ШИФРИ СКЛАДНОЇ ПЕРЕСТАНОВКИ30
- 31. 2.1. Шифри перестановки з використанням гамильтонових маршрутів31
- 32. Досить високу стійкість шифруванню можна забезпечити, використовуючи
- 33. 33Рис. 4.6. Схема шифрування перестановкою по маршрутах Гамильтона
- 34. 34 На цьому рисунку, у лівій частині, по-
- 35. При використанні гамільтонова марш- руту, якій наведений: -
- 36. Варто помітити, що всі процедури шифрування й
- 37. 2.2. Шифри перестановки з використанням магічних квадратів 37
- 38. У середні століття для шифрування перестановкою застосовувалися
- 39. Якщо потім виписати зміст такої таб- лиці
- 40. Рис. 4.7. Нумерація букв переданого повідомлення при
- 41. Рис. 4.8. Приклад магічного квадрата розміром 4х4
- 42. Число магічних квадратів швидко зростає зі збільшенням
- 43. Шифри перестановки надзвичай- но підступні в тому
- 44. Слайд 44
- 45. Слайд 45
- 46. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Сіденко Володимир Павлович,
Старший викладач кафедри “Безпека інформаційних та комунікаційних систем”
1
ЗМІСТОВНИЙ
МОДУЛЬ № 1
Слайд 4Питання лекції № 5
1. Криптографічні системи, які використовують шифри простої
перестановки
2. Криптографічні системи, які використовують шифри складної перестановки
Література: Л2, с.
17 – 20, 113 - 125; Л3, с. 54 – 65.4
Слайд 6 При використанні для шифрування ін- фомації методів перестановки символи відкритого
тексту переставляються відпо- відно до певних правил.
У ручних шифрах у
древні часи часто використовували таблиці, які дають прос- ті процедури, що шифрують - перестановки букв у повідомленні. Ключем у них служать розмір таблиці, фраза, що задає переста-новку або спеціальну особливість таб-лиць.6
Слайд 8 Проста перестановка без ключа - один з найпростіших методів шифрування.
Наприклад,
повідомлення
НЕЯСНОЕ СТАНОВИТСЯ ЕЩЕ
БОЛЕЕ НЕПОНЯТНЫМ
записується в таблицю по стовпцях.
Результат заповнення таблиці
з 5 ряд-ків і 7 стовпців показаний на рис. 4.1.8
Слайд 10 Після того, як відкритий текст запи- саний стовпчиками, для утворення
шифро- текста він зчитується по рядках.
Якщо його записувати групами по
7 букв, то вийде:НОНСБНЯ ЕЕОЯОЕТ ЯСВЕЛПН
СТИЩЕОЫ НАТЕЕНМ
Для використання цього шифру від- правникові й одержувачеві потрібно домо- витися про загальний ключ у вигляді роз- міру таблиці й способів запису та зчиту- вання символів у таблицю або з таблиці.
10
Слайд 11 Об'єднання букв у групи не входить у ключ шифру й
використовується лише для зручності запису тексту.
Більше практичний метод шифруван- ня,
якій називається поодинокою переста-новкою по ключі дуже схожий на поперед- ній.Він відрізняється лише тим, що ко- лонки таблиці переставляються по ключо-вому слову, фразі або набору чисел довжи-ною в рядок таблиці.
11
Слайд 12 Використовуємо у вигляді ключа сло-во ЛУНАТИК, а текст повідомлення візьме-
мо з попереднього приклада.
На рис. 4.2 показані дві таблиці, за-
повнені текстом повідомлення й ключем, при цьому таблиця (рис. 4.2,а) відповідає заповненню до перестановки, а таблиця (рис. 4.2,а) - після перестановки.12
Слайд 15 У верхньому рядку таблиці на рис. 4.2,а записаний ключ, а
номера під ключем визначені за природним порядком відпо- відних букв
ключа в алфавіті.Якщо в ключі зустрілися б однакові букви, вони б нумерувалися ліворуч – пра- воруч.
Після здійснення перестановки стовп- ців, як показано на рис. 4.2,б, виходить зашифроване повідомлення:
СНЯННБО ЯЕТЕООЕ ЕПНЯВЛС
ЩОЫСИЕТ ЕНМНТЕА.
15
Слайд 1616
При шифруванні методом простої замі- ни можна використовувати і числові
ключі. Нехай числовий ключ для попереднього прикладу має вигляд: 7,
5, 2, 4, 1, 6, 3.На рис. 4.3 показані дві таблиці, запов- нені текстом повідомлення й ключем, при цьому таблиця (рис. 4.3,а) відповідає запо- вненню до перестановки, а таблиця (рис. 4.3,б) - після перестановки.
Слайд 1919
У верхньому рядку таблиці на рис. 4.3,а стовпчики пронумеровані природно.
Після здійснення перестановки стовпців, відповідно до ключу, як показано на
рис. 4.3,б, виходить зашифроване повідомлен-ня: ЯБОСННН ТОЕЯЕЕО НЛСЕЯПВ ЫЕТЩСОИ МЕАЕННТ.Слайд 21 Крім одиночних перестановок по стовпчиках використовувалися ще перес- тановки стовпців
і рядків таблиці з пові- домленням одночасно. При цьому перес-
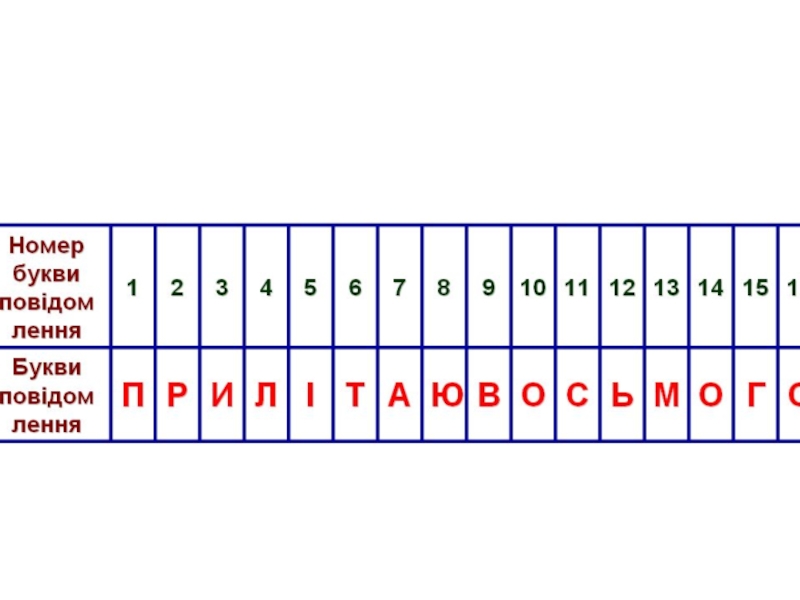
тановки визначалися окремо для стовпців і окремо для рядків. У таблицю вписувався текст і переставлялися стовпці, а потім рядки. При розшифровці порядок перес- тановок буде зворотний.Приклад виконання шифрування мето- дом подвійної перестановки повідомлення ПРИЛІТАЮ ВОСЬМОГО показаний на рис. 4.4.
21
Слайд 23 Нехай ключем до шифру подвійної пе- рестановки служить послідовність номерів
стовпців і номерів рядків вихідної таблиці (у нашому прикладі послідовності
4, 1, 3, 2 і 3, 1, 4, 2 відповідно).На початку в таблицю на рис. 4.4,а впи- сується відкритий текст, по стовпчикам, потім здійснюється перестановка стовпців, а потім – рядків по послідовностях стовп- ців – 4, 1, 3, 2, а рядків – 3, 1, 4, 2. Якщо зчи- тувати шифротекст із таблиці, яка наведена на рис. 4.4,в по рядках блоками з чотирьох букв, то вийде наступне ГИСА МПВI ОЛЬЮ ОРОТ.
23
Слайд 24 При розшифровці порядок перестано- вок буде зворотний. Покажемо на прикладі
розшифрування шифротексту ГИСА МПВI ОЛЬЮ ОРОТ (див. рис. 4.5).
24
Слайд 26 Зчитуючи символи з таблиці рис. 4.5,в з початку за стовпчиками,
а потім за рядка- ми отримуємо розшифрований шифро- текст: ПРИЛІТАЮ
ВОСЬМОГО.Число варіантів подвійної перестанов- ки швидко зростає при збільшенні розміру таблиці:
- для таблиці розміром 3x3: 36 варіан- тів:
- для таблиці розміром 4x4: 576 ва- ріантів;
- для таблиці розміром 5x5: 14400 ва- ріантів.
26
Слайд 27 Для додаткової скритності можна пов- торно шифрувати повідомлення, що вже
було зашифровано. Цей спосіб відомий за назвою подвійна перестановка. Для
цього розмір другої таблиці підбирають так, щоб довжини її рядків і стовпців були інші, чим у першій таблиці. Найкраще, якщо вони будуть взаємно простими. Крім того, у першій таблиці можна переставляти стовпці, а в другий - рядки. Нарешті, можна заповнювати таблицю зиґзаґом, змійкою, по спіралі або якомусь іншому способу.27
Слайд 28 Такі способи заповнення таблиці якщо й не підсилюють стійкість шифру,
то роб- лять процес шифрування набагато більше цікавим.
Перевагою криптографічних системи,
які використовують шифри табличної пере- становки є те, що для них слабо застосо- вується метод криптоаналізу – частотний аналіз.28
Слайд 29 Якщо проаналізувати шифротексти при використанні поодиноких та подвій- них перестановок,
то ми побачимо, що во- ни не відрізняються високою стійкістю
й порівняно просто "зламується" при будь- якому розмірі таблиці шифрування.ВИСНОВКИ
29
Слайд 32 Досить високу стійкість шифруванню можна забезпечити, використовуючи уск- ладнений метод
перестановок по марш- рутах типу гамильтонових.
При цьому для запису символів
тексту, якій шифрується використовуються вер-шини деякого гіперкуба, а знаки зашиф-рованого тексту зчитуються по маршрутах Гамильтона, причому використовується кілька різних маршрутів (рис. 4.6).32
Слайд 3434
На цьому рисунку, у лівій частині, по- казані гамильтонові маршрути
для фор- мування шифрограм (шифротекстов).
У розглянутому прикладі можливе шифрування текстів
блоками з довжиною 8 букв .Нехай, передане повідомлення
КРИПТОГР
Це повідомлення записується відпо- відно до гамильтонових маршрутів, які на- ведені у правій частині рис. 4.6.
Слайд 35 При використанні гамільтонова марш- руту, якій наведений:
- в лівій верхній
частині рис. 4.5, фор- мується шифрограма:
ТОРКИПРГ - ключ 4→5→1→0→2→3→ 7→6;
а наведеного в нижній правій частині:ТКИПРОРГ - ключ 4→0→2→3→1→5→ 7→6.
35
Слайд 36 Варто помітити, що всі процедури шифрування й розшифрування за методом
перестановки є в достатньому ступені фор- малізованими і можуть бути
реалізовані ал- горитмічно.36
Слайд 38 У середні століття для шифрування перестановкою застосовувалися й магічні квадрати.
Магічними
квадратами називають квадратні таблиці з вписаними в їхні клі- тинки
послідовними натуральними числа- ми, починаючи від 1, які дають у сумі по кожному стовпці, кожному рядку й кожній діагоналі те саме число.Відкритий текст уписували в магічні квадрати відповідно до нумерації їхніх клі- тинок.
38
Слайд 39 Якщо потім виписати зміст такої таб- лиці по рядках, то
вийде шифротекст, якій сформований завдяки перестановці букв вихідного повідомлення.
У ті
часи вважалося, що створені за до-помогою магічних квадратів шифротексти охороняє не тільки ключ, але й магічна си-ла.Нехай повідомлення, що шифрується має вигляд: ПРИЛІТАЮ ВОСЬМОГО.
Для використання магічного квадрата проведемо нумерацію букв повідомлення, що шифрується, як це показано на рис. 4.7.
39
Слайд 40Рис. 4.7. Нумерація букв переданого повідомлення при використання магічного квадрата
Приклад
магічного квадрата і його за- повнення повідомленням ПРИЛІТАЮ ВОСЬМОГО показаний
на рис. 4.8.40
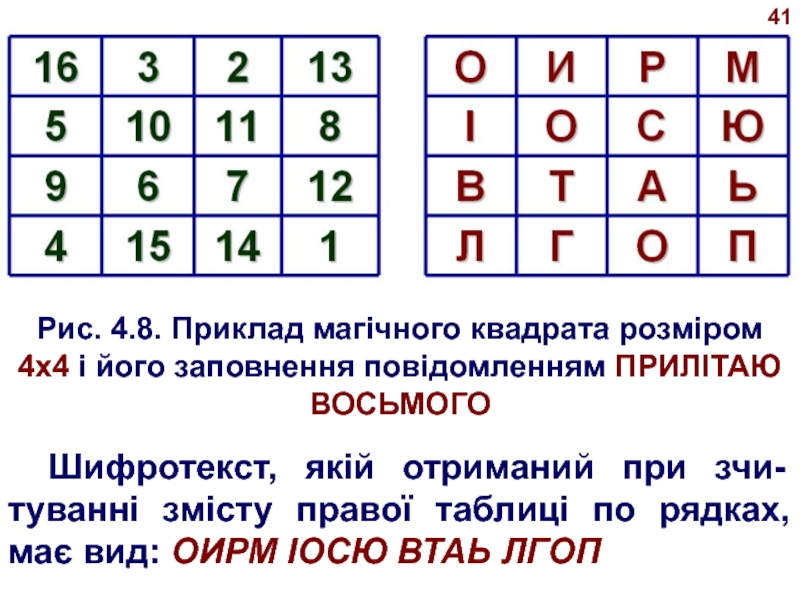
Слайд 41Рис. 4.8. Приклад магічного квадрата розміром 4х4 і його заповнення
повідомленням ПРИЛІТАЮ ВОСЬМОГО
Шифротекст, якій отриманий при зчи- туванні змісту правої
таблиці по рядках, має вид: ОИРМ ІОСЮ ВТАЬ ЛГОП41
Слайд 42 Число магічних квадратів швидко зростає зі збільшенням розміру квадрата.
Існує тільки
один магічний квадрат розміром 3х3 (якщо не враховувати його повороти).
Кількість магічних квадратів 4x4 становить уже 880, а кількість магічних квадратів 5х5 - близько 250000.Магічні квадрати середніх і більших розмірів могли служити гарною базою для забезпечення потреб шифрування того ча- су, оскільки практично нереально виконати вручну перебір всіх варіантів для такого шифру.
42
Слайд 43 Шифри перестановки надзвичай- но підступні в тому розумінні, що мо-
жуть дати декілька варіантів осмис- леного прочитання, якщо не знати
точного значення ключа.ВИСНОВКИ
43