Симплекс метод

виду;
определение начального неотрицательного базисного решения.
2.Общая характеристика метода и демонстрация его

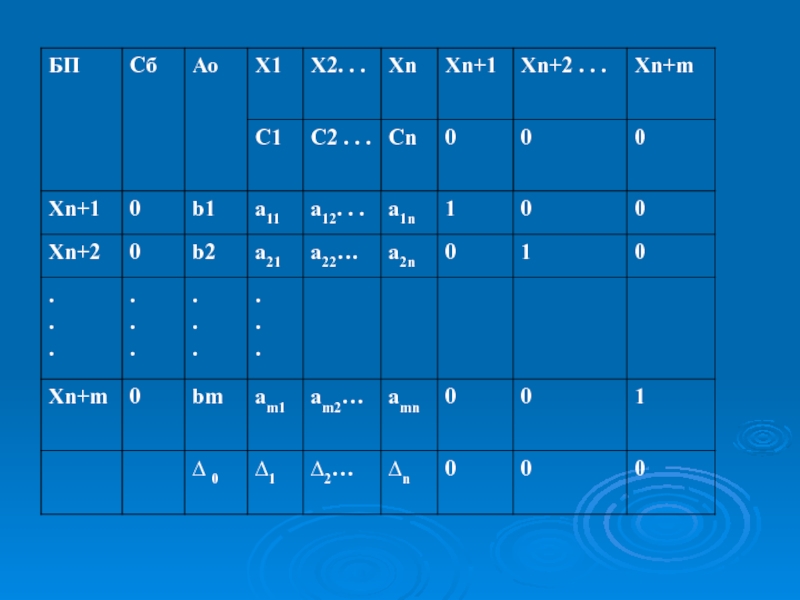
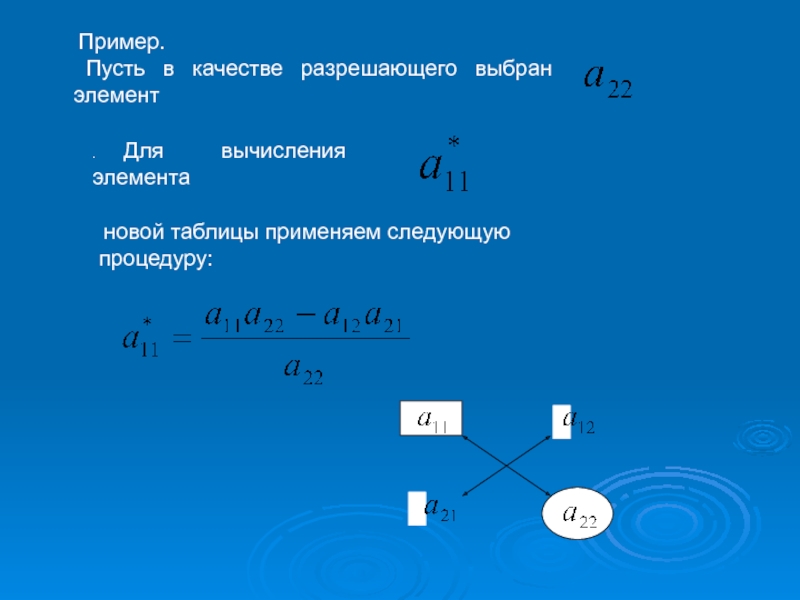
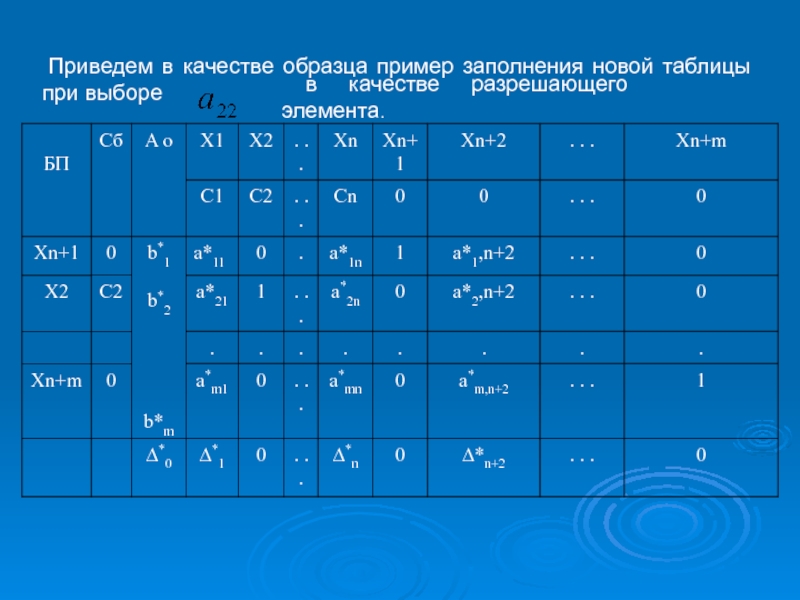
применения на примере.
3.Симплексные таблицы.
4.Общее представление о симплекс-методе с искусственным базисом

исходной задачу определения оптимальной производственной программы, записанную в симметричном виде.

Для изменения формы записи задачи используем неотрицательные балансовые переменные, которые добавим к левым частям неравенств. В целевую функцию введем балансовые переменные с нулевыми коэффициентами.

наличия такого решения следующий: в каждом уравнении системы ограничений должна

присутствовать такая переменная, которая в данном уравнении имеет коэффициент 1, а в остальных уравнениях системы коэффициент 0. Таким образом, в матрице системы должна выделяться единичная подматрица.

задачи на максимум Z позволяет сразу выделить единичную подматрицу и

базисное решение.
2. Матрицу системы можно преобразовать методом «Жордана-Гаусса» и получить в итоге единичную подматрицу и базисное решение
3. Можно ввести искусственные переменные и сформировать единичную подматрицу их коэффициентами

переменных, которые именуются базисными. Остальные переменные будем называть свободными.
Выразив

базисные переменные через свободные и приравняв последние к нулю, получаем базисное решение.
Поскольку свободные члены уравнений в силу их физического смысла являются числами неотрицательными, полученное базисное решение неотрицательно.

Если значение целевой функции нельзя улучшить, то данное базисное решение

является оптимальным; если – можно, то начинаем переход к другому базисному решению
Выбираем свободную переменную, способную обеспечить максимальное изменение значения целевой функции. Эту переменную вводим в состав базисных таким способом, который позволяет сохранить неотрицательное значение всех остальных переменных. Получаем новый состав базисных и свободных переменных и новую запись целевой функции.

запись целевой функции, которая подтверждает невозможность получения дальнейшего прироста ее

значения. Так, при решении задачи на максимум Z, это будет выражение, в котором все переменные имеют отрицательные коэффициенты. Делаем вывод: данное базисное решение является оптимальным.

задачи симплекс-методом. Для ее заполнения достаточно убедиться в наличии начального

неотрицательного базисного решения.
Для получения оптимального решения, как правило, недостаточно одной таблицы.
Переход от одной таблицы к другой осуществляется по определенным правилам.

– вектор коэффициентов, стоящих в целевой функции при базисных

переменных; – вектор свободных членов ограничений; – коэффициенты при переменных в ограничениях; - значение целевой функции при начальном базисном решении; – оценки свободных переменных.
Для расчета используем формулу = Оценки рассчитываем так
где - вектор коэффициентов при соответствующей переменной.

строкой оценок

Если в данной строке при решении задачи

на максимум целевой функции все

а при решении на min все

то начальное базисное решение и является оптимальным.
Если существуют

не удовлетворяющие данному требованию, то необходимо продолжить поиск оптимального решения.

положительных при решении на min) выбираем наибольшую по модулю. В

соответствующем ей столбце

среди положительных коэффициентов

выделяем разрешающий элемент, для которого отношение

является минимальным.

состав компонентов вектора Замену определяет местоположение разрешающего элемента;
Переносим

без изменений столбцы тех переменных, которые остались базисными;
На месте разрешающего элемента ставим 1, на остальные места в данном столбце ставим 0. Остальные места в строке заполняем числами, полученными путем деления прежних компонентов на разрешающий элемент;
Остальные компоненты таблицы определяем по «правилу прямоугольника»

вычисления элемента
новой таблицы применяем следующую процедуру:

пересчитываемого элемента формируем прямоугольник;
Из произведения элементов, стоящих на концах основной

диагонали, включающей разрешающий элемент, вычитаем произведение элементов на концах второстепенной диагонали;
Полученную разницу делим на разрешающий элемент

выборе
в качестве разрешающего элемента.

неотрицательны при решении на max (или неположительны при решении на

min), то оптимальное решение получено. В противном случае процедура повторяется.
Ответ задачи состоит из оптимальных значений переменных

и экстремального значения Z. Экстремум целевой функции размещен в ячейке

оптимальные значения базисных переменных находятся в столбце

значения свободных переменных равны нулю.

которых получение исходного неотрицательного базисного решения сопряжено с трудностями (транспортная

задача);
Достоинство подхода в том, что он позволяет ускорить подготовку задачи к применению вычислительной процедуры симплекс-метода;
Недостаток – увеличение числа переменных делает модель более громоздкой

частям уравнений, образующих систему ограничений задачи. В целевую функцию эти

переменные включаются с коэффициентом «-М» при решении задачи на максимум и «+М» при решении задачи на минимум целевой функции. «М» символизирует бесконечно большое положительное число. Задача решается симплекс-методом. Оптимальное решение М-задачи является также и оптимальным решением исходной задачи.