Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Системы линейных уравнений и способы их решения
Содержание
- 1. Системы линейных уравнений и способы их решения
- 2. 1. Общий вид, основные понятия, матричная формаСистема
- 3. Система линейных уравнений (СЛУ)Совместная(имеет хотя бы одно
- 4. Любую СЛУ можно представить в
- 5. 1) Метод обратной матрицыМетод основан на нахождении
- 6. 2) Метод последовательного исключения неизвестных (Метод Гаусса)Рассмотрим СЛУ:Данный метод применим к СЛУ любой размерности.
- 7. Алгоритм метода:Составим расширенную матрицу.2. С помощью элементарных
- 8. Элементарными преобразованиями матрицы называют:Умножение какой-нибудь строки (столбца)
- 9. 3) Метод КрамераМетод основан на вычислении определителей, поэтому применим к СЛУ размерности nxn.Рассмотрим СЛУ:
- 10. Введем следующие обозначения:Теорема. Если
- 11. Δ =а11 а12 ... a1na21
- 12. 3) Составим определитель - Δ2Δ2=а11 b1
- 13. Скачать презентанцию
1. Общий вид, основные понятия, матричная формаСистема m линейных уравнений с n неизвестными имеет вид:где коэффициенты при неизвестных, свободные коэффициенты.
Слайды и текст этой презентации
Слайд 21. Общий вид, основные понятия, матричная форма
Система m линейных уравнений
с n неизвестными имеет вид:
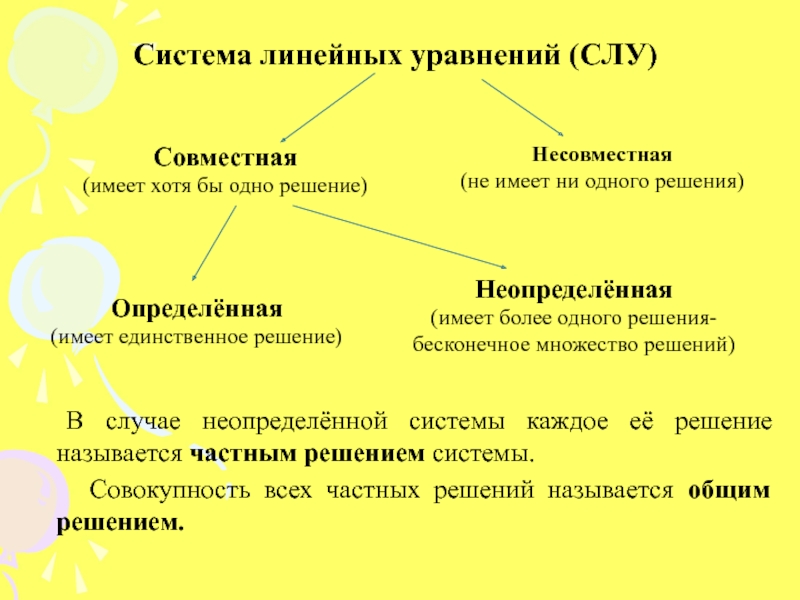
коэффициенты.
Слайд 3Система линейных уравнений (СЛУ)
Совместная
(имеет хотя бы одно решение)
Несовместная
(не имеет ни
одного решения)
Определённая
(имеет единственное решение)
Неопределённая
(имеет более одного решения-
бесконечное множество решений)
В
случае неопределённой системы каждое её решение называется частным решением системы. Совокупность всех частных решений называется общим решением.
Слайд 4 Любую СЛУ можно представить в матричном виде:
- матричный вид исходной СЛУ.
А – основная матрица системы, В – матрица-столбец свободных членов,
Х – матрица-столбец неизвестных
Слайд 51) Метод обратной матрицы
Метод основан на нахождении обратной матрицы, поэтому
применим к СЛУ размерности nxn.
Рассмотрим СЛУ в матричном виде:
Слайд 62) Метод последовательного исключения неизвестных (Метод Гаусса)
Рассмотрим СЛУ:
Данный метод применим
к СЛУ любой размерности.
Слайд 7Алгоритм метода:
Составим расширенную матрицу.
2. С помощью элементарных преобразований строк расширенную
матрицу приведём к треугольному (ступенчатому) виду.
3. Вернувшись к системе
уравнений, находим неизвестные.
Слайд 8Элементарными преобразованиями матрицы называют:
Умножение какой-нибудь строки (столбца) на отличное от
нуля число.
Прибавление к какой-нибудь строке (столбцу) другой её строки (столбца),
умножение на любое число, отличное от нуля.Перестановку местами любых двух строк.
Слайд 93) Метод Крамера
Метод основан на вычислении определителей, поэтому применим к
СЛУ размерности nxn.
Рассмотрим СЛУ:
Слайд 10Введем следующие обозначения:
Теорема. Если
, то СЛУ имеет единственное решение
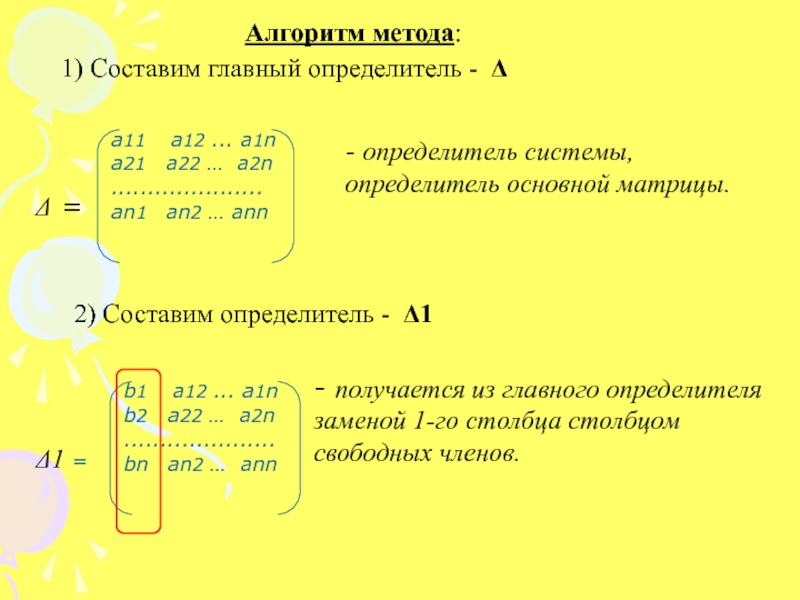
, где . (Формулы Крамера)
Слайд 11Δ =
а11 а12 ... a1n
a21 a22 … a2n
.....................
an1
an2 … ann
- определитель системы, определитель
основной матрицы.Δ1 =
b1 а12 ... a1n
b2 a22 … a2n
.....................
bn an2 … ann
- получается из главного определителя заменой 1-го столбца столбцом свободных членов.
1) Составим главный определитель - Δ
2) Составим определитель - Δ1
Алгоритм метода:
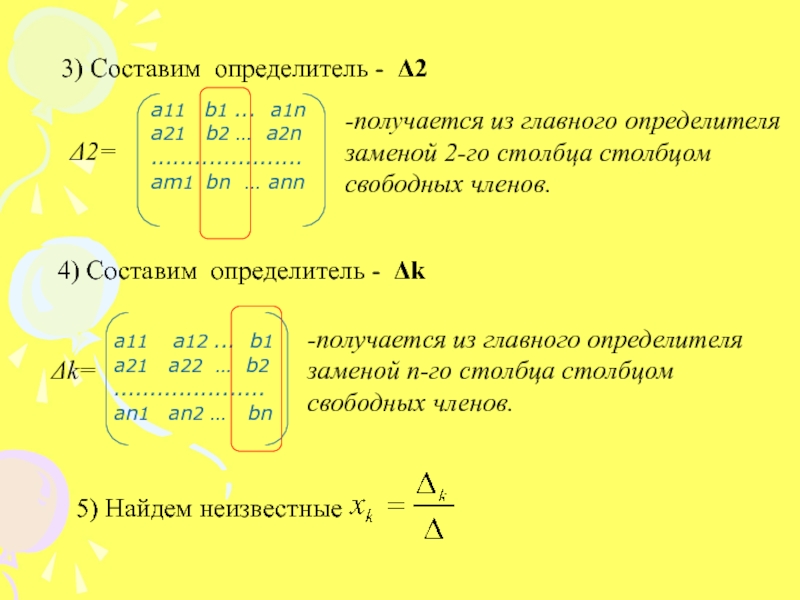
Слайд 123) Составим определитель - Δ2
Δ2=
а11 b1 ... a1n
a21
b2 … a2n
.....................
am1 bn … ann
-получается из главного определителя
заменой 2-го столбца столбцом свободных членов.4) Составим определитель - Δk
Δk=
а11 а12 ... b1
a21 a22 … b2
.....................
an1 an2 … bn
-получается из главного определителя заменой n-го столбца столбцом свободных членов.
5) Найдем неизвестные
